基于模糊神经网络与主成分分析的磨削表面粗糙度在线预测

迟玉伦, 吴耀宇, 江 欢, 杨 磊

(上海理工大学,上海200093)

1 引 言

影响磨削加工过程中的工件表面粗糙度的因素众多,包括进给速度、磨削量、砂轮速度、砂轮修整状况、工件材料的成分及加工过程中的一些不确定因素等[1-2]。磨削过程是动态的,磨削用量、工件材料、磨削振动等诸多影响表面粗糙度因素在不断变化,工件表面粗糙度的监测流程影响加工质量和加工效率。如能实现对工件表面粗糙度进行实时检测,及时控制生产过程中的加工参数,则可避免人力、原料和加工时间上的浪费[3,4]。

通过在线监测加工过程中的相关物理量可以进行实时预测表面粗糙度[5～7],如振动加速度信号、声发射信号等能够有效地反映工件表面粗糙度的变化,使用传感器信号建立预测模型实现表面粗糙度的在线预测。在使用振动信号进行预测方面,迟军等[8]利用振动信号的小波包分析和松散型小波网络实现了表面粗糙度的在线预测。Upadhyay V和 Risbood K A等[9,10]根据振动信号的时域分析法对信号进行处理,并结合切削参数实现表面粗糙度的在线监测。Plaza E G等[11]提出在时域上使用奇异谱分析方法且仅通过经验正交函数对振动信号进行分析,监测在线加工的表面粗糙度。在使用声发射信号预测方面,胡仲翔等[12]使用改进的BP神经网络,以磨削声发射信号的特征量作为输入,对表面粗糙度进行了预测。王艳等[13]利用声发射信号的小波包分解的能量特征,对慢走丝线切割加工的表面粗糙度进行了预测。郭力等[14]采用遗传算法优化BP神经网络,以声发射均方根和快速傅里叶变换峰值为特征值,对铸铁表面粗糙度进行了预测。以上均采用振动信号或声发射信号的特征量,单一传感器信号易受外界干扰,可能存在信息量不足的问题,未能充分利用传感器在加工过程中所传递的有效信息,使得建模过程耗时繁琐并且可能会造成较大的预测误差。

受加工过程中诸多因素的影响,在进行表面粗糙度的预测时,不同学者选择加工参数也不尽相同。孙林等[15]提出基于最小二乘支持向量机仅使用磨削用量来预测。汪振华等[16]根据试验分析得到影响表面粗糙度的显著影响因素被进刀量、每齿进给量、主轴转速,并使用最小二乘法建立模型对切削加工的防锈铝合金表面粗糙度预测。陈廉清等[17]使用遗传算法与反向传播神经结合,以进给速度、工件转速和进给量为输入进行粗糙度预测。郑刚等[18]通过模糊优选理论对材料去除率、总铣削力和残余应力3个因素进行优先判断,并建立模型进行粗糙度预测。这些方法多通过构建表面粗糙度与加工参数、刀具、工件材料等经验因素的关系模型进行预测,因模型的选择与参数调整不一,导致不同的模型预测精度较低。

针对上述存在的问题,本文在声发射与振动信号相结合使用的基础上,提出了主成分分析(principle components analysis，PCA)与模糊神经网络(fuzzy neural network，FNN)结合的表面粗糙度预测模型。首先,采集磨削加工过程中的声发射信号振动加速度信号；然后,提取两种信号的主要时域、频域和小波包特征,并使用PCA方法进行处理得到选择最优特征量,且避免高维非线性特征处理的复杂性。使用FNN进行模型构建,建立了表面粗糙度预测模型；最后,对磨削工件的表面粗糙度进行了预测验证。

2 表面粗糙度预测原理

2.1 磨削加工过程中表面粗糙度的影响因素

磨削过程中是砂轮直接与工件接触,因此表面粗糙度的产生直接与砂轮单位面积磨粒量、磨粒的分布情况及磨粒切削痕迹等有关,其形成过程如下[19]：如果砂轮转速na与工件转速nsσ之间成整倍数关系,则砂轮表面粗糙度将同样复印在工件表面上,n次与n+1磨粒切削刃痕迹如图1所示。实际磨削过程中,na/nsσ不是整数,磨粒切削刃将不会重复切削工件表面上的同一点,切削刃痕迹将相互错开[20]。

图1 n次与(n+1)次磨粒切削刃痕迹Fig.1 Cutting edge traces of n times andn+1) times abrasive grains

由于表面粗糙度的影响因素较多,仅通过特定单一信号进行预测,很难得到高精度的预测结果。因此,本文采用在线监测相关信号(如声发射信号和振动加速度信号)来实现表面粗糙度实时识别,需要充分挖掘并利用信号中包含的有效信息。

2.2 表面粗糙度预测流程

在加工的过程中,工件表面粗糙度越大,则相同压力作用下的摩擦产生的应力波强度越大,声发射现象越明显,建立表面粗糙度与声发射信号特征值与的映射关系,就可以实现磨削过程中表面粗糙度的实时在线监测[21,22]。由振动理论可知,机床系统的振动是由激振源及系统的结构特性决定,与磨削粗糙度存在一定关系[23]。在机床上安装声发射传感器及三向振动传感器,采集磨削过程中的高频声发射信号及振动加速度信号,提取信号中的特征量并进行降维处理,降维后的特征量作为模型输入,输出为预测的工件表面粗糙度。

首先,将采集到的数据进行信号预处理,将其中的异常点剔除。其次,使信号特征提取,对于采集到的信号,特征值的变化也会映射出工件表面粗糙度的变化,提取的信号特征量包括时域特征、频域特征和小波包特征；提取的特征量有许多,需要通过特征降维方法得到与表面粗糙度相关的主特征量。最后,通过FNN进行表面粗糙度的预测,预测流程如图2所示。

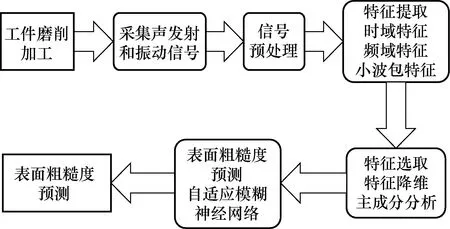
图2 表面粗糙度预测流程Fig.2 Surface roughness prediction process

3 表面粗糙度预测模型研究

3.1 声发射信号与振动信号特征选择

工件表面粗糙度的大小与信号的时域特征、频域特征和小波包特征存在相关性。在时域特征中,均值表示信号的中心趋势,均方根表示信号的平均能量,峭度因子表示大幅值脉冲出现的概率,裕度因子反映了信号的冲击程度。因此时域特征可选取为平均值、均方根、峭度因子、裕度因子。频域特征的变化与表面粗糙度的变化也有很大相关性。重心频率,均方频率和均方根频率均表示信号功率谱中主频带的位置变化情况,频率方差和频率标准差描述谱能量的分散程度。因此，选择的频域特征有重心频率、均方频率、均方根频率、频率方差和频率标准差。由于小波包分析中含有大量的信号信息[24],故小波包特征选取为小波包4层分解后各子频带的统计特征,选择的统计特征有平均值、均方根、峭度因子、裕度因子。

从信号中提取的特征值有：振动信号x、y、z方向的时域特征、频域特征,声发射信号的时域特征、频域特征和小波包特征,共99维特征。

3.2 PCA降维方法

PCA是一种特征的主成分提取方法[25]。在提取特征主成分之前对输入空间进行归一化处理,将原始特征数据标准化。

PCA的计算步骤如下：

(1)计算信号样本数据xi矢量的协方差矩阵C公式

(1)

式中xi为信号样本数据矢量。

(2)求出C的特征值λi及对应的单位正交特征矢量ui

λiui=Cui

(2)

前m个较大的特征值λ1≥λ2≥…>λm>0,代表前m个主成分的特征矢量ui就是主成分Fi关于原变量的系数。主成分的方差贡献率表示信息量,信息量越大表明所含原数据的信息越多,信息量的大小αi

(3)

若前m个主成分的累积贡献率大于85%,则提取的主成分特征可反映原来高维特征的信息。

(3 )计算主成分得分,计算信号样本的主成分

U=[u1,u2,…,um]T
F=ATU

(4)

式中：U为特征向量矩阵；A为信号样本数据xi的矩阵；F是特征的主成分矩阵,即为压缩降维后的特征数据,得到的低维特征将用于表面粗糙度的预测模型输入。

3.3 FNN结构

使用FNN结构来表达各个降维主成分与表面粗糙度的映射关系。将降维处理后的数据集分为训练集和测试集两部分,选用训练集对预测模型进行训练,然后用测试集来测试预测模型的准确性[26]。在FNN中,模糊系统的输入、输出信号用输入、输出节点来表示,隶属函数和模糊规则用神经网络的隐含节点来表示,模糊系统的推理能力因神经网络的并行处理能力而大大提高。

图3为FNN的基础结构图。

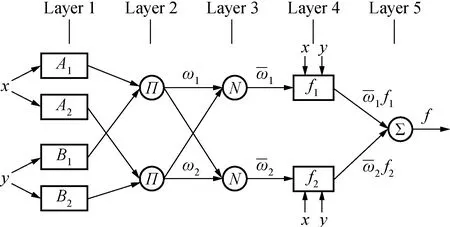
图3 FNN结构Fig.3 Structure of FNN

本文基于遗传算法的FNN的粗糙度识别模型基于此结构进行构建。该FNN是一个多层前馈网络,其中的方形节点需要进行参数学习[27]。第1层为输入变量的隶属函数层,负责输入信号的模糊化,节点具有输出函数；

(5)

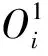
第2层为规则的强度释放层Π。每个输入信号都来自第1层,此层的节点为固定节点不能进行训练。

(6)

式中ωi为第2层的输出。

第3层为所有规则强度的归一化N。表示每一条模糊规则的激励强度占所有规则激励强度的百分比。此层的节点为固定节点,不能进行训练。

(7)

第4层为模糊规则的计算输出f,这1层的每个节点均为自适应节点,此层参数是自适应的, 可根据输入数据训练得到。其输出为

(8)

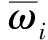
在给定前提参数后,结论参数的线性组合可作为自适应模糊神经推理系统的输出：

(9)

3.4 FNN自学习

为使FNN其具有自学习能力,将遗传算法应用到该网络模型,使其成为是一个多层前馈网络。其优化算法可分为两个步骤：

(1) 确定前提参数的初始值, 用最小二乘法计算结论参数。则由式(9)得到：

(10)

式中：结论参数集合{p1,q1,r1,p2,q2,r2}构成列向量X的元素；若已有P组输入输出数据对, 且给定前提参数, 则矩阵A、X、f的大小为P×6,6×1和P×1。

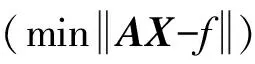
X′=(ATA)-1ATf

(11)

(2) 根据上一步计算得到的结论参数进行误差计算,采用前馈神经网络中的遗传算法,将误差由输出端反向传到输入端, 用梯度下降法更新前提参数, 从而改变隶属函数的形状。

4 实验设计

实验平台如图4所示。在一台平面磨床上使用夹具固定磨削工件,机床为KP-48T数控平面磨床,工件材料为GCr15,使用砂轮进行磨削加工。实验使用一个声发射传感器及一个振动传感器,声发射传感器采用KISTLER-8443B,传感器的频率范围为2 MHz。振动传感器为三向振动传感器,传感器的频率范围为5～3 kHz,测量范围为0～50 Gal,声发射信号采样率为2×106/s,三向振动信号采样率为 2 000 Hz。

为了准确获得磨削过程中加工信号,声发射传感器和振动传感器均有磁性底座,将其吸附在用于固定工件的金属夹具上,放置位置见图4。

设计不同的磨削加工参数砂轮速度、进给速度、磨削量进行正交试验,正交实验表如1所示。

表1正交试验表Tab.1 Orthogonal test table

图4 实验平台Fig.4 Experimental platform

为提高数据的可靠性,测量时在工件表面选取4个点,其测量值Ra的算术平均值作为实验数据。图5为实验过程中采集到的声发射传感器与振动传感器的原始信号。

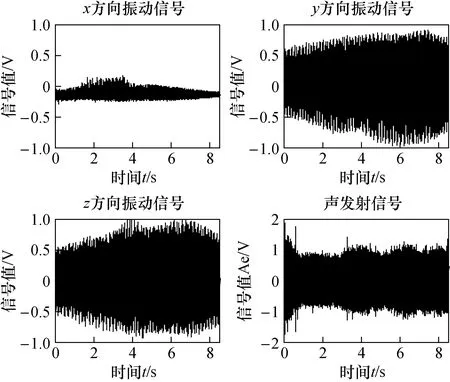
图5 声发射传感器与振动传感器原始信号Fig.5 Original signal of acoustic emission sensor and vibration sensor

5 实验结果与对比分析

5.1 信号处理与主成分降维

对采集到的声发射信号与振动加速度信号进行处理,根据前文已选择的特征值进行提取,使用Matlab软件对信号进行时域分析、频域分析、小波包分析,所提取到的特征值有振动信号x、y、z方向的时域特征、频域特征,声发射信号的时域特征、频域特征和小波包特征,共99维特征。

图6为主成分降维的按贡献率大小的前六维特征值以及主成分的累积贡献率。可以看出前五维特征值的累积贡献率为86.3%,可有效保留原维度特征值的信息,即通过PCA将99维特征空间降维为五维特征空间。

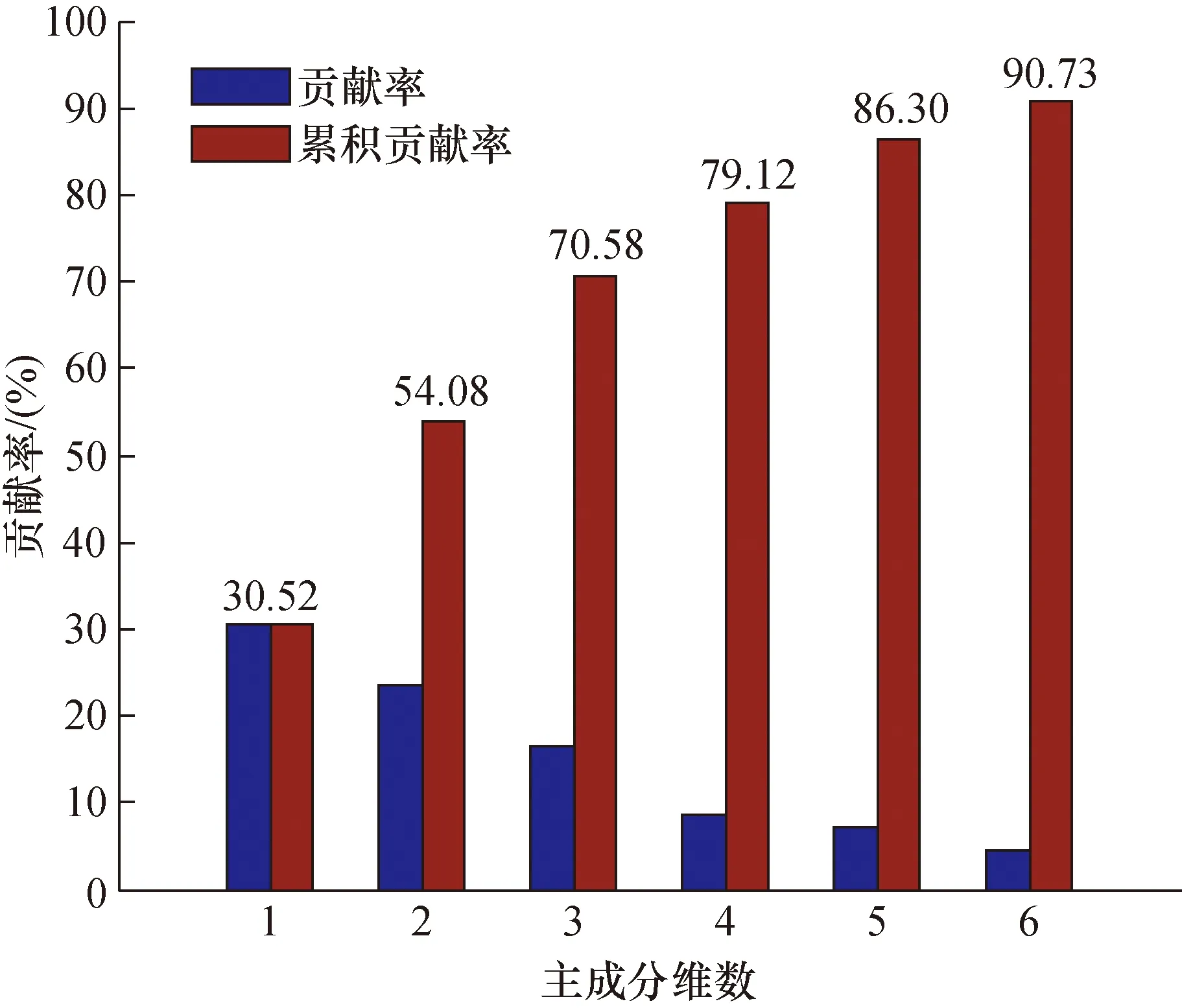
图6 PCA各成分贡献率与累积贡献率Fig.6 The contribution rate and cumulative contribution rate of each component of the principal component analysis

表2为选取的9组实验降维后的五维主成分特征值与每组实验的表面粗糙度值。

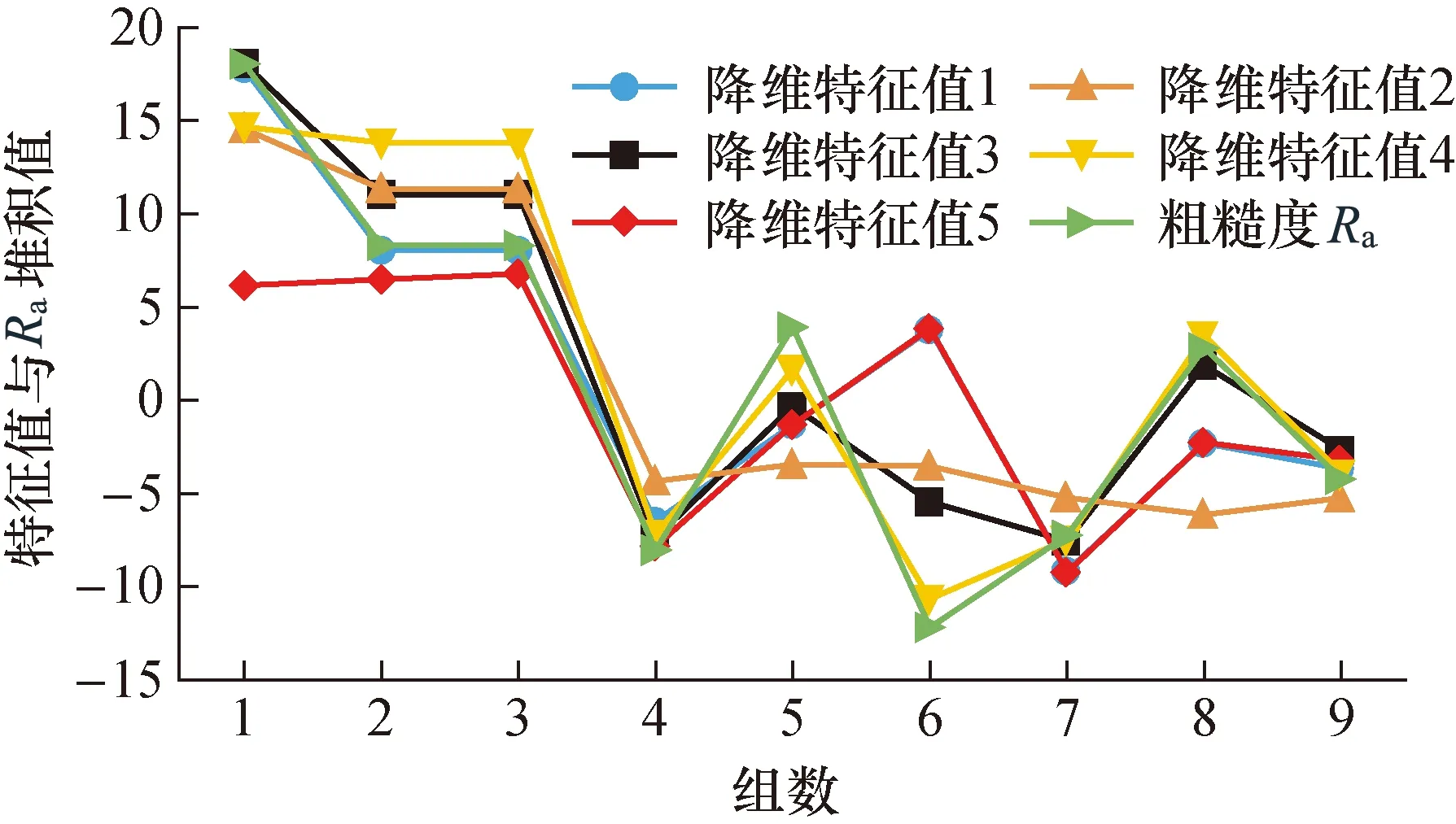
图7 各降维特征值与表面粗糙度堆积折线图Fig.7 Stacked line graph of each dimensionality reduction eigenvalue and surface roughness

图7所示为5个降维特征值与对应表面粗糙度的堆积折线图,可以看出大多降维特征的变化趋势与表面粗糙度值得变化趋势高度相关,为表面粗糙度预测模型提供了基础。

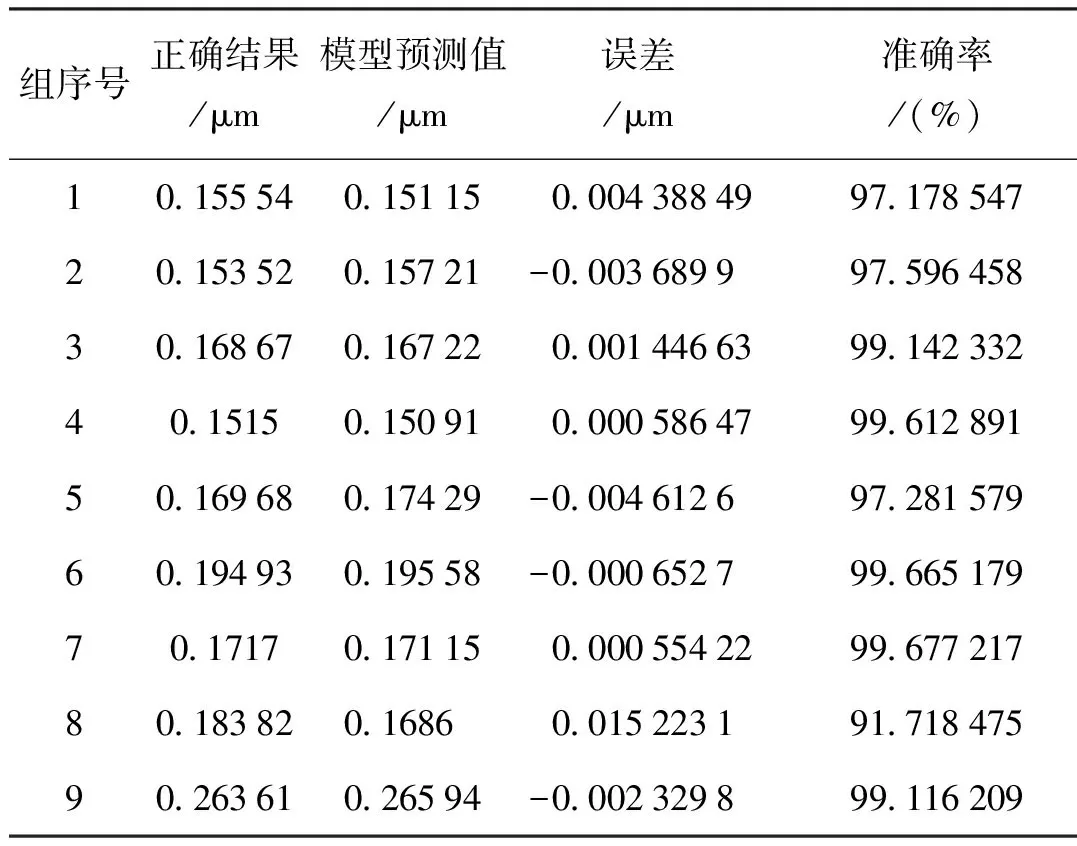
表2模型预测值与正确值Tab.2 Model predicted value and correct value

5.2 模糊神经表面粗糙度预测模型的训练与验证

使用FNN构建模型对表面粗糙度进行预测,其结构为图3所示的5层结构。输入层节点为5个降维特征值,选择高斯函数作为初始隶属度函数,输出层为工件表面粗糙度。

选择每组实验信号处理后的5个特征值为5个输入,对应的工件表面粗糙度作为输出,建立了基于声发射与振动信号的主成分FNN模型。选择9组实验数据作为测试集,得到模型的预测值。

模型的预测值与正确值如图8所示,图9为模型预测值与正确值的误差范围,可以看出模型的预测范围在10%以内,可以得出模型预测结果的有效性。

图8 模型预测结果与正确值Fig.8 Model prediction results and correct values

图9 预测结果的误差范围Fig.9 The error range of the prediction results

表2是利用声发射信号和振动信号的主成分FNN模型的预测结果与实际测量值的误差来预测准确率。根据表2数值对比显示,模型的预测结果误差范围为[-0.046 126 μm, 0.015 223 1 μm ],平均误差仅为0.001 212 66 μm,准确率可达到91%以上,预测值非常接近实际值,体现了该模型预测的准确性和可靠性。

5.3 降维方法结果对比分析

为验证使用PCA方法具有较好的降维效果,选取降维方法局部线性嵌入(locally linear embedding,LLE )和多维标度法 (multidimensional scaling,MDS)分别对相同的特征值数据样本进行降维,并使用FNN进行模型训练,这两种降维方法的模型预测结果与PCA分析降维的模型预测结果进行对比。

图10为LLE和MDS降维方法建立的模型的表面粗糙度预测的结果。

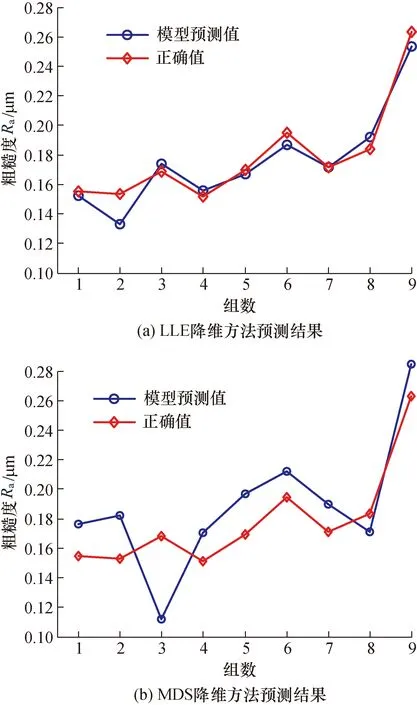
图10 LLE和MDS降维方法模型预测结果Fig.10 Model prediction results of LLE and MDS dimensionality reduction method

图11为使用LLE和MDS降维算法模型预测误差范围。

可以看出LLE降维方法与MDS降维方法建立的预测模型得出的结果误差均大于10%,对比PCA方法建立的预测效果误差模型(10%以内),准确度要低。

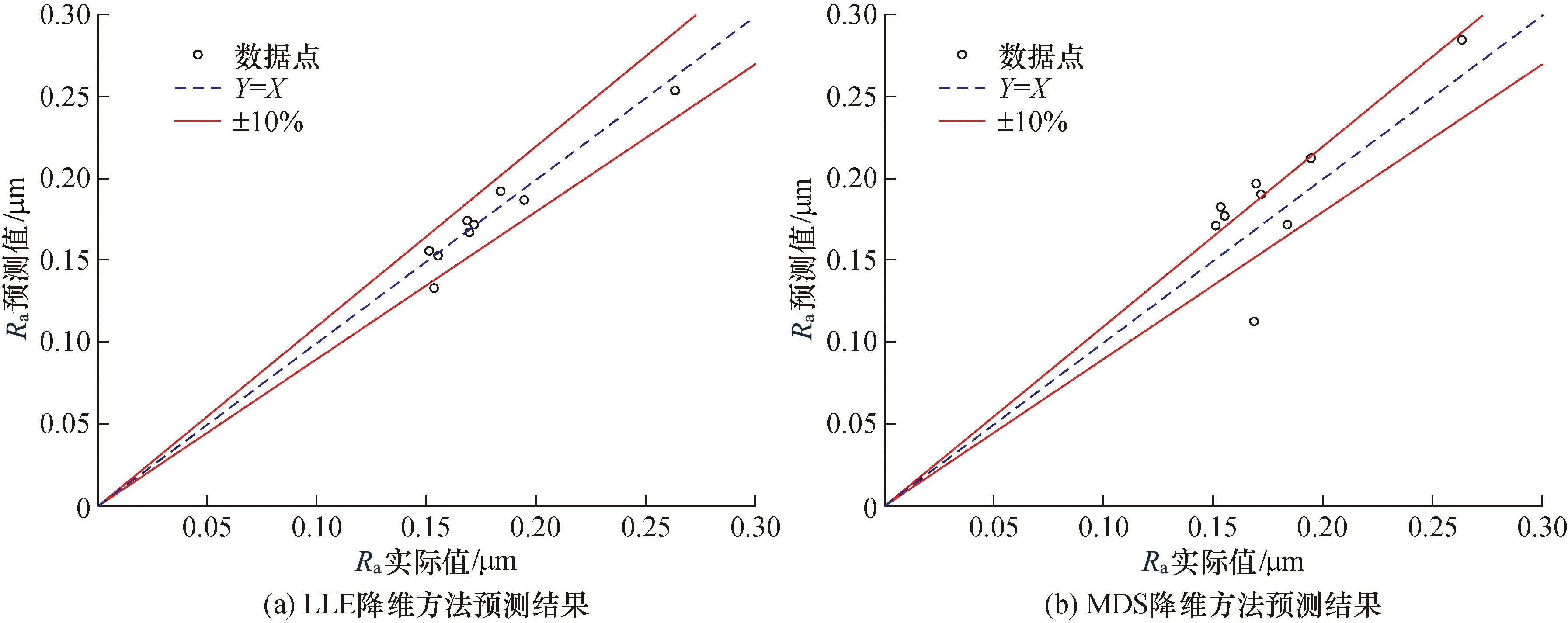
图11 LLE和MDS降维算法模型预测误差范围Fig.11 LLE and MDS dimensionality reduction algorithm model prediction error range reduction method

表3与表4分别为LLE降维方法模型的预测结果误差与正确率。

由表3、4可知LLE降维方法的模型预测准确率最低为86.6%,MDS降维方法模型预测准确率最低为66.6%,由表2可知主成分降维方法模型预测准确率最低为91.7%,对比可知PCA方法所建立的预测模型预测效果优于使用LLE降维方法和使用MDS降维方法所建立的预测模型。

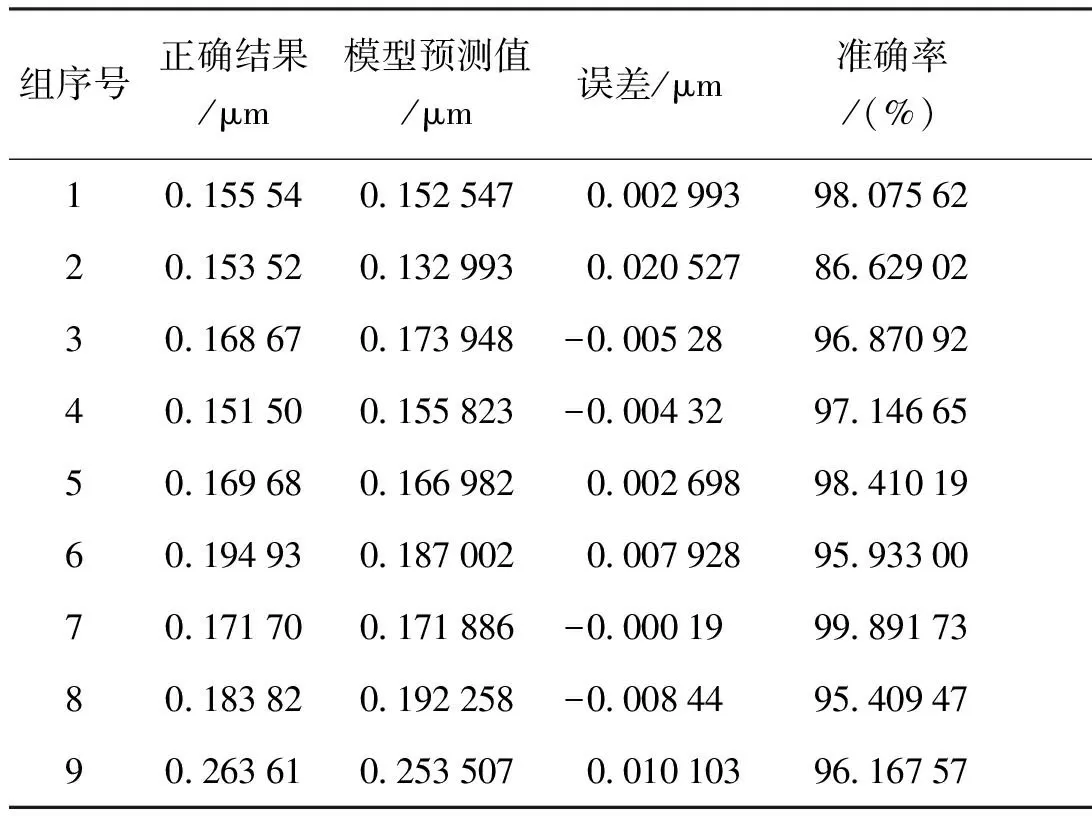
表3LLE降维方法模型预测结果与正确率Tab.3 Model prediction results and accuracy of LLE dimensionality reduction method

为进一步比较出3种降维方法模型预测的准确性,使用相关系数(r2)、均方根差(RMSE)两种统计指标进行对比。r2是用来反映两种参数相关关系密切程度的统计量,其数值范围为0～1,数值越大说明模型预测值与正确值的相关程度越高,准确度越高。RMSE是用来反映两组数值之间差异程度的度量,数值越小,说明模型预测值与正确值的差距越小。

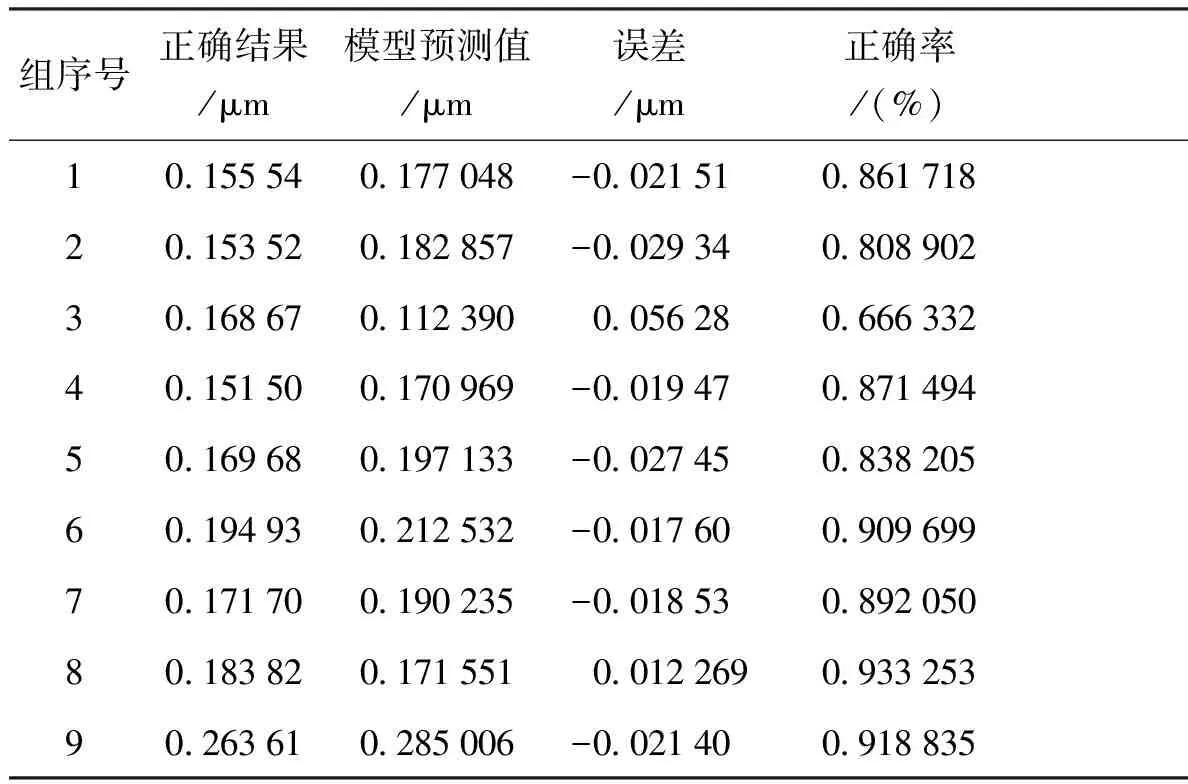
表4MDS降维方法模型预测结果与正确率Tab.4 Model prediction results and accuracy of MDS dimensionality reduction method

表5为3种模型的相关系数与均方根差的对比,主成分降维所建立的模型相关系数值最高,均方根差值最低,说明其预测结果与正确值相关程度最高,模型的预测效果最好。

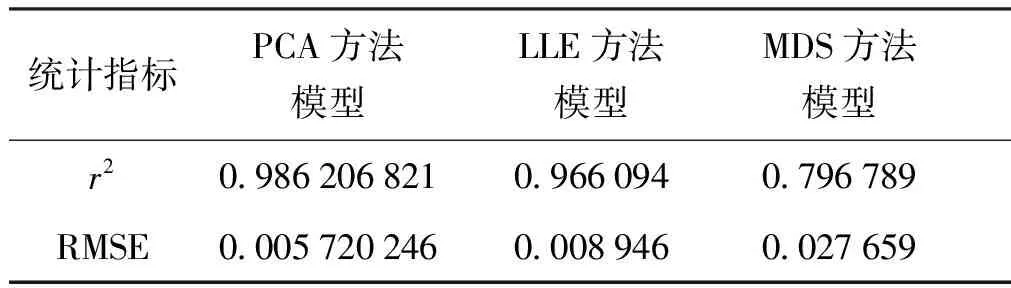
表53种降维方法模型的正确值与预测值统计指标Tab.5 Statistical indicators of correct and predicted values of the three dimensionality reduction methods

通过上面预测结果图与误差范围图的对比和表2 与表3、4的对比以及表5的分析可以看出,使用PCA方法信号特征降维处理建立的模糊神经模型预测效果最好,可靠性更好。

6 结 论

针对表面粗糙度预测模型输入参数依靠人工经验选择,造成模型预测精度低的问题,使用声发射信号与振动信号进行充分信息提取,并使用特征降维方法对模型输入进行优化处理,实现工件表面粗糙度的准确预测。实验结果表明：

(1) 根据声发射与振动原理,选择磨削加工过程中的这两种信号可以进行表面粗糙度的预测,根据模型的预测结果,两种信号在很大程度上反映了加工过程中表面粗糙度的状态。

(2) 使用PCA方法对高维特征值进行降维处理,以保留85%以上数据信息的方式,得到了传感器信号的5个主成分特征,优化了特征值参数。与LLE和MDS降维方法相比,PCA的降维效果更好,所建立的模糊神经预测模型准确度更高,准确率可达到91%以上。

(3) 通过监测传感器信号及实时数据处理,可以间接实现加工过程中工件表面粗糙度的预测。由于FNN并行处理数据,计算速度较快,故本文方法能够实时、高效、准确地对表面粗糙度进行检测。