黑河上中游月径流序列多重分形特性研究

朱新丽, 李彦彬, 李红星, 杜雪芳

(华北水利水电大学 水利学院, 河南 郑州 450046)

人类活动和气候变化致使水文序列的非平稳性愈加明显,分析的复杂性增加。运用分形理论对径流序列的非线性规律进行研究,能发现水文过程的非均匀结构特性,深化对水动力机制的认识,全面揭示水文系统的复杂运动特征。HURST H E在1951年发现水文时间序列存在长程相关性[1],到1969年MANDELBROT B B等[2]把分形理论与水文系统的非线性动力机制联系起来。随之,国际上展开了对径流序列分形特征分析的研究[3-6]。

去趋势波动分析(Detrended Fluctuation Analysis,DFA)[7]法是基于经典随机行走(random walk)的单分形分析方法,可有效滤去时间序列各阶段趋势成分[8],与R/S等常规分析方法相比,可有效消除非平稳序列中伪相关现象。然而DFA无法对非线性时间序列进行精确地分析和刻画。2002年KANTELHARDT J W等[9]在DFA法的基础上提出了多重分形去趋势波动分析(Multifractal Detrended Fluctuation Analysis,MF-DFA)方法,相比DFA法有着更加丰富的内容,不仅可用标度指数、分形维数,还可用多重分形谱来描述分形体不同层次的目标特征。MF-DFA方法解决了噪声和信号波动对重分形谱计算的影响,适合于任意数据长度的数字计算,但其计算复杂,对参数敏感性极大。2005年LASHERMES B等[10]提出了小波领袖(Wavelet Leaders,WL)方法,解决了小波系数和小波变换模极大值(Wavelet Transform Modulus Maxima,WTMM)方法在多重分形分析计算中存在的不稳定、计算量庞大以及数学基础缺乏等问题,更容易处理正值和负值,能有效处理振荡奇点和尖点奇点[11]。

有研究表明,序列的周期性波动对长期记忆的检测会产生显著的影响,导致检测到并不存在的长期记忆[12]。日尺度和月尺度的径流时间序列,含有显著的季节周期性,这在一定程度上导致径流时间序列出现“虚假回归”的现象,这种“虚假回归”现象在很大程度上影响分形结果的准确性和可靠性[13]。因此,在进行黑河上中游月径流时间序列分形计算之前,本文运用基于局部加权回归的周期趋势分解(seasonal-trend decomposition procedure based on loess,STL)方法对数据进行预处理,以消除季节周期波动对分形结果的影响。

黑河是我国西北第二大内陆河,黑河流域是一个资源缺水型流域。引入分形理论,分析黑河流域月径流序列的分形特性,对全面认识黑河水动力运动特征,揭示其径流系统在复杂变化环境下的演变规律,是非常有必要的。为揭示黑河上中游月径流量演变的主要原因,本文采用小波领袖多重分形分析(Wavelet Leaders for Multifractal Analysis,WLMF)方法和2阶MF-DFA(MF-DFA2)方法对STL季节分解前、后的黑河上中游札马什克站、祁连站、莺落峡站和正义峡站的月径流序列进行分析。

1 研究方法与研究区概况

1.1 STL季节分解

STL方法由CLEVELAND R B等[14]在1990年为解决从复杂时间变化数据中提取趋势和季节性变化成分的问题而提出的,它可以稳健处理任何类型的季节性数据,且在数据出现少数异常观测值时,不会影响模型对趋势和季节性周期因素的估计。STL方法主要应用于水质模型中[15-16],近两年国内研究者才开始将其应用于其他方向[17-19]。

STL方法可将时间序列X分解为季节项、趋势项和随机项,分解表达式如下:

X=XS+XT+XR。

(1)

式中:X为月径流量,亿m3;XS为高频季节项;XT为低频趋势项;XR为随机分量。

STL季节分解过程中,季节项平滑参数(nS)和趋势项平滑参数(nT)是最重要的2个参数,分别控制提取趋势项和季节项时取样窗口的宽度。一般季节项平滑参数与数据的时间跨度相关,为略大于时间跨度的奇数。趋势项平滑参数满足:

(2)

式中nP为一个周期内的样本数量。

1.2 多重分形去趋势波动(MF-DFA)

2002年，KANTELHARDT J W等[9]在DFA方法基础上提出了MF-DFA方法,该方法可以同时对平稳和非平稳时间序列的结构及涨落特性进行度量。MF-DFA方法主要包括5个步骤:

1)计算时间序列{xt}(t=1、2、…、N;N为序列长度)的累积离差Y(i):

(3)

2)将Y(i)按等长度S分成不重叠的NS个区间,NS=[N/S],运算符[ ]表示取整数。由于序列长度并不总是S的整数倍,这就会导致小部分数据信息不能被利用。为使所有数据信息都能被利用,可对Y(i)的逆序进行同样操作,则共有2NS个等长度的区间。

3)用最小二乘法对每个区间v进行多项式拟合,得到局部趋势。然后计算每个区间滤去趋势后的方差F2(v,S):

(4)

(5)

式中yv(i)为第v个区间的拟合多项式。如果拟合多项式采用的阶数为m,式(4)和(5)中可以消除原始序列中m-1阶的趋势成分。

4)对所有2NS个等长度区间求和,计算q阶DFA波动函数Fq(S):

(6)

(7)

当q=2时,公式(6)是标准DFA的计算公式。为考察不同q值的波动函数Fq(S)与时间尺度S的关系,可改变S值,重复第2—4步。

5)在每个q的(S,Fq(S))双对数图上,考察波动函数的标度行为。如果时间序列{xt}是长程幂律相关的,那么Fq(S)与S存在以下关系:

Fq(S)～Sh(q)。

(8)

对公式(8)进行最小二乘法线性拟合,即可得到广义Hurst指数h(q)。

一般当h(q)<0.5时,时间序列表现出反持久性;当h(q)>0.5时,时间序列表现出持久性。若h(q)随着q表现为幂律函数关系时,则h(q)显著依赖于q,表明序列具有多重分形特性。此时,时间序列具有不同的标度行为:q>0时,Fq(S)的大小取决于F2(v,S)较大的波动,h(q)刻画了大涨落的标度行为;q<0时,Fq(S)的大小取决于F2(v,S)较小的波动,h(q)描述了小涨落的标度行为。一般在多重分形分析中,大涨落的h(q)小于小涨落的h(q)。

由Renyi尺度指数可知,广义Hurst指数h(q)与质量指数τ(q)存在如下关系:

τ(q)=qh(q)-1。

(9)

若τ(q)与q呈线性关系,表明时间序列是单分形结构。若两者存在非线性关系,说明时间序列为多重分形结构,且非线性关系越显著,序列的多重分形特征就越显著。

利用Legendre变换,得:

(10)

式中α为奇异指数。α越大,信号的局部奇异性就越弱,正则性越强,信号就越平滑;反之,信号在该区间范围内奇异性就越强,正则性越弱,局部变化越剧烈。分形谱的宽度Δα可用来描述多重分形谱奇异性强度的范围:

Δα=αmax-αmin。

(11)

Δα越大,时间序列分布就越不均匀,多重分形强度越大;Δα越小,则时间序列趋向于单分形。

1.3 小波领袖多重分形(WLMF)

小波领袖法[10]是基于离散小波变换的分形方法,它通过特定的方案搜寻不同尺度上小波系数的最大值。

对于序列X,其离散小波变换系数dX(j,k)为:

(12)

式中:ψ0(t)为具有紧支撑的小波母函数;ψj,k(t)(j,k∈Z)为通过对母小波进行平移和伸缩产生的函数集合。

定义λ=λj,k=[2jk,2j(k+1)]为2的幂次方间隔,用3λ表示λ与其相邻的并集,即:

3λj,k=λj,k-1∪λj,k∪λj,k+1。

(13)

则小波领袖为:

(14)

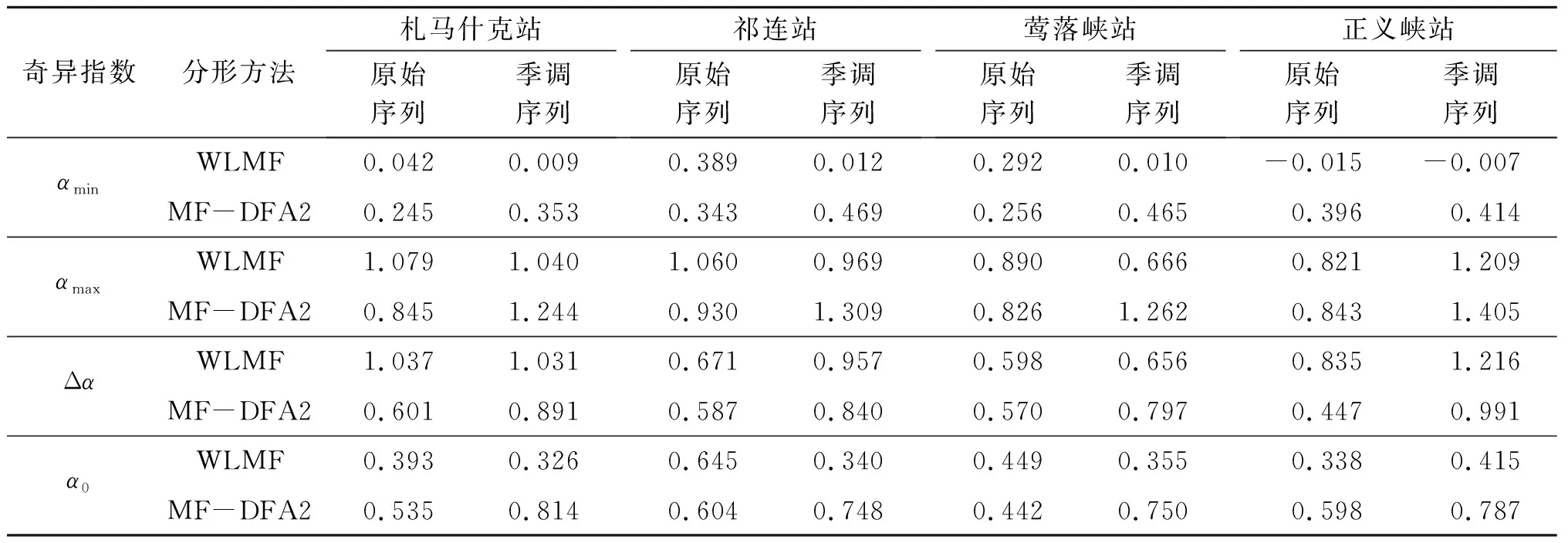
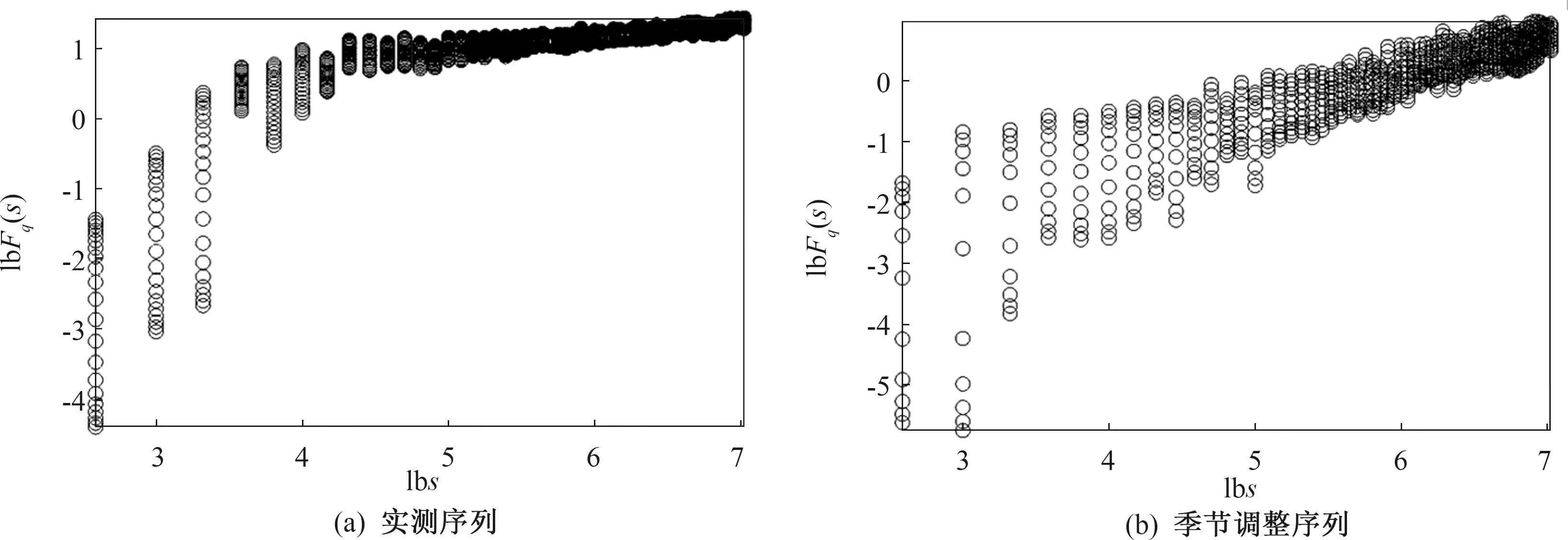
LX(j,k)是邻域为2j′(k-1)≤k′j′<2j(k+2),尺度为2j′≤2j的所有小波尺度中的上确界,即LX(j,k)等于在所有{2j|0

小波领袖能为多重分形分析提供多分辨率的变量,并能刻画奇异性。其结构函数SL(q,j)与分解尺度2j满足SL(q,j)～(2j)ζL(q)(2j→0)。结构函数和尺度函数分别表示为:

(15)

(16)

式中nj为当尺度取2j时的小波领袖的个数。

根据Legendre变换,可以得到基于小波领袖的多重分形奇异谱参数:

(17)

WENDT H等[20]利用参数公式避免了Legendre变换,简化了多重分形谱的计算,即:

(18)

(19)

(20)

(21)

(22)

(23)

(24)

1.4 研究区概况

黑河发源于河西走廊和祁连山中段冰川区,对环境的响应较为敏感,受气候变化和人类活动影响严重。莺落峡水文站以上为黑河上游,西支有札马什克水文站,东支有祁连水文站。上游地势高峻,气候严寒湿润,植被较好,是黑河水的主要来源区,黑河流域径流主要受降水、融冰融雪等影响。春季径流以地下水补给和冰雪融水为主,夏季和秋季以降水补给为主。每年的10月到次年的3月河流处于冰冻期,为枯水季节,径流量小而稳定,地表径流量占年径流总量的20%左右;4—6月(春末夏初),随着气温升高,祁连山区冰雪融化,水量增加,地表径流量上升;7—9月为梅雨季节,降水量急剧增加,同时冰川融水量也达到最大,达地表径流量的50%以上。

莺落峡站是黑河干流出山口控制站,莺落峡站至正义峡站断面为中游,是径流利用区,受人为因素影响强烈,径流年内分配变化显著。每年的3—5月为春灌高峰期,此时河流处于冰冻期，河水径流量小,黑河下泄水量很少,河床甚至出现断流现象,因而正义峡站以下地表径流量处于年内最低值;6月河水流量开始增加,7—9月为汛期,9月灌溉回归水和地下水大量溢出,形成年内径流高峰;10月由于冬季灌溉和降水量的减少,河水流量再度减少,11月达到最低值;12月到次年3月为非农业用水季节,中游用水量减少,地下水补给相对稳定,河流量平稳。正义峡站断面以下为下游,主要为沙漠戈壁,下游属极端干旱区,也是我国北方沙尘暴的主要来源区之一。

本文采用的数据资料为:札马什克站1959.01—2017.12、祁连站1968.01—2017.12、莺落峡站1954.01—2018.12、正义峡站1963.01—2012.12的实测月径流量。研究区水系如图1所示。

2 结果与分析

2.1 季节分解

对黑河上中游4个水文站的实测月径流序列进行STL季节分解,分解结果如图2所示。由于本文时间序列为月数据,因此nP取12。各水文站月径流序列STL分解后的季节项和趋势项平滑参数取值见表1。

图2 各水文站月径流序列STL季节分解图

表1 各水文站实测月径流序列STL分解平滑参数

由图2可知,各水文站实测月径流序列具有周期性,但并没有固定的周期循环波动特征,分解后的月径流序列表现出显著固有的稳定周期性。其中札马什克站、祁连站和莺落峡站的月径流序列具有稳定的、单一的季节周期波动特征,正义峡站的月径流序列具有多个周期特征。说明札马什克站、祁连站和莺落峡站的月径流序列的周期波动仅与季节变化有关,而正义峡站月径流序列的周期波动不仅与季节波动有关,还与人类周期活动有关。

2.2 多重分形分析

在分析时间序列的多重分形性质时,MF-DFA方法通常假定一个宽泛的时间尺度,即标度s。一般取s∈[6,N/6],其中N为时间序列的长度。

札马什克站、祁连站、莺落峡站、正义峡站的月径流序列在WLMF和MF-DFA2方法下的尺度函数谱和多重分形谱分别如图3—6所示,图中季节调整序列为实测月径流序列经STL分解后去除季节周期项的序列。

图3 札马什克站月径流序列的尺度函数谱和多重分形谱

图4 祁连站月径流序列的尺度函数谱和多重分形谱

图5 莺落峡站月径流序列的尺度函数谱和多重分形谱

图6 正义峡站月径流序列的尺度函数谱和多重分形谱

图3(a)—图6(a)的尺度函数谱显示,各水文站时间序列的尺度函数τ(q)与q呈明显的非线性关系,且呈凸的递增函数关系,可见各水文站的月径流时间序列都具有多重分形特性。基于MF-DFA2方法的多重分形分析显示:在消除季节周期波动影响后,各水文站月径流序列的尺度函数τ(q)与q的关系曲线的斜率增大,说明时间序列的周期性波动对分形参数的估计产生影响,且在消除季节周期波动影响后月径流序列变化更剧烈;曲线斜率在q<0时比在q>0时变化明显,说明MF-DFA2方法对参数敏感性在q<0时比q>0时大。基于WLMF方法的分析结果显示:在消除季节周期波动影响后,札马什克站、祁连站和莺落峡站τ(q)与q的关系曲线的斜率在q<0时没有发生显著变化,但在q>0时减小,这与MF-DFA2方法的分析结果不同,这是由于时间序列较短导致WLMF方法的计算结果出现偏差;正义峡站τ(q)与q的关系曲线斜率在q<0时增大,在q>0时没有发生变化,与MF-DFA2方法的分析结果一致。

图3(b)—图6(b)的多重分形谱显示,各水文站时间序列的多重分形谱为凸曲线,说明各水文站的月径流序列具有多重分形特性。经季节调整后,序列的多重分形谱发生变化,说明季节周期波动会对分形结果产生影响。对于实测月径流序列:札马什克站和正义峡站的月径流序列相对较短,两种分形计算方法的结果相差较大;祁连站和莺落峡站的月径流序列相对较长,两种分形计算方法的结果基本一致,这与WLMF方法受时间序列长短的影响有关;WLFM和MF-DFA2两种方法的计算结果显示,札马什克站、祁连站和莺落峡站月径流序列多重分形谱的宽度Δα在q>0时比q<0时小,表明α较大的部分占优势,月径流序列的变化主要是由小涨落引起;正义峡站月径流序列多重分形谱的宽度Δα在q>0时与q<0时基本一致,说明小涨落和大涨落对月径流序列的影响同等重要。与实测序列相比,WLMF方法下各水文站季节调整月径流序列的多重分形谱向左偏,MF-DFA2方法下多重分形谱向右偏,说明季节周期波动对分形结果有影响;其中图6(b)显示,在q>0时正义峡站季节调整后月径流序列的多重分形谱与实测序列相比变化不显著,在q<0时季节调整后月径流序列的多重分形谱显著向右偏,说明季节周期波动对q<0时正义峡站月径流序列的多分形特性有影响。

各水文站月径流序列在不同分形计算方法下的奇异指数特征见表2。

表2 各水文站月径流序列奇异指数特征值

表2显示,消除季节周期影响后各水文站月径流序列多重分形谱的宽度(Δα)普遍增大,序列变得不均匀,多重分形强度增大。对于实测月径流序列,札马什克站、祁连站、莺落峡站和正义峡站Δα的均值分别为0.819、0.629、0.584、0.641,消除季节周期影响后,各水文站Δα的均值分别为0.961、0.898、0.726、1.104,可见,消除季节周期影响后各水文站月径流序列多重分形谱的宽度增大。这说明黑河上中游月径流序列的分布不均匀性增强,多重分形强度增大,则季节周期波动是引起黑河上中游月径流量变化的原因之一。其中,正义峡站的Δα在4个水文站中最大(1.104),其变化也最大。但图6(b)的分析结果显示,季节周期波动主要影响q<0时正义峡站月径流序列的分形特性,而MF-DFA2分形方法对q<0时表现得最为敏感,因此只能说明季节周期波动对正义峡站月径流量有影响,但影响程度不显著。根据表2分析结果可知,札马什克站、祁连站和莺落峡站月径流序列的多重分形特征主要受季节周期波动的影响,且从黑河上游到中游月径流序列的分形强度在减弱,不均匀性在减小。

各水文站月径流序列的广义Hurst指数h(q)随阶数q的变化情况如图7所示。

图7 各水文站月径流序列广义Hurst指数

由图7可知,各水文站月径流序列的广义Hurst指数h(q)随阶数q的递增而递减,表明黑河上中游月径流序列具有多重分形特性。基于MF-DFA2方法,莺落峡站实测月径流序列h(2)<0.5,札马什克站、祁连站和正义峡站实测月径流序列h(2)>0.5,即莺落峡站实测月径流序列具有反持久性,札马什克站、祁连站和正义峡站实测月径流序列具有持久性;消除季节周期影响的各水文站月径流序列h(q)均大于0.5,普遍大于实测月径流序列h(q),且在q<0时比q>0时变化显著,说明季节周期波动降低了月径流序列持久性的强度,同时也说明了MF-DFA2方法在q<0时更敏感。基于WLMF方法,札马什克站、莺落峡站和正义峡站实测月径流序列h(2)<0.5,祁连站实测月径流序列h(2)>0.5;消除季节周期影响后,各水文站月径流序列h(2)均小于0.5,与MF-DFA2方法所得结论相反。这说明两种方法对季节周期波动的响应不同,而WLMF方法受序列长短影响。因此,WLMF方法不适用于札马什克站和正义峡站。

在MF-DFA2方法下各水文站月径流序列在季节调整前、后的配分函数图分别如图8—11所示。图中(F(s),s)的双对数坐标图上直线部分的斜率,即为h(q)的估计值；q∈[-10,10]。对比各水文站去除季节周期波动趋势前、后的配分函数关系图发现,在去除季节周期波动趋势后,札马什克站、祁连站和莺落峡站月径流序列的lbFq(s)与lbs之间的非线性程度大大减小。图8—10显示,札马什克站、祁连站和莺落峡站实测月径流序列配分函数曲线的斜率在lbs=3.5～4.0(即第10—16个月)时发生突变,而消除季节周期波动趋势后lbFq(s)与lbs之间表现出显著的线性关系,且突变点消失,说明实测月径流序列中,季节周期波动是导致lbFq(s)发生不规则变化的主要原因,突变点是由信号的季节周期波动产生的。但q取负值时,波动函数曲线在更小的尺度范围仍然有弯曲情况,表明还有其他因素(如噪声)对月径流序列产生影响。在消除季节周期波动前、后,正义峡站波动函数Fq(s)与尺度s的线性关系只在q<0时有变化,但不显著,说明引起正义峡站lbFq(s)产生不规则变化的主要原因不在于季节周期波动,而与人类活动有关。

图8 札马什克站月径流序列MF-DFA2配分函数关系图

图9 祁连站月径流序列MF-DFA2配分函数关系图

图10 莺落峡站月径流序列MF-DFA2配分函数关系图

图11 正义峡站月径流序列MF-DFA2配分函数关系图

3 结语

本文运用WLMF和MF-DFA2方法,对STL季节分解前、后的黑河上中游札马什克站、祁连站、莺落峡站和正义峡站的月径流序列进行多重分形分析。通过对两种分析方法的函数尺度谱和多重分形谱、奇异指数特征值和广义Hurst指数进行对比,以及对MF-DFA2方法下的配分函数关系图进行分析,结果显示:黑河上中游月径流序列具有多重分形特性;其中,莺落峡站实测月径流序列具有反持久性,札马什克站、祁连站和正义峡站实测月径流序列具有持久性;黑河上游月径流序列的长程相关性主要由季节周期波动引起,从札马什克站到莺落峡站月径流序列的分形强度减弱,不均匀性减小;而正义峡站月径流序列的不均匀性主要与人类活动有关。

本研究中,径流时间序列的长度相对较长(大于600个月),但对于WLMF方法而言,月径流时间序列的长度仍不能满足该方法对时间序列长度的要求,导致WLMF方法和MF-DFA2方法的多重分形分析结果存在误差。因此,在今后的研究中需选取更长的径流序列来讨论两种分形分析方法下黑河上中游月径流序列的多重分形特性及其影响因素。