基于GARCH类模型沪深300股指期货波动率预测研究

沈慈慈，王伟杰，侯为波

（1.淮北师范大学 数学科学学院，安徽 淮北 235000；2.淮北理工学院 教育学院，安徽 淮北 235000）

0 引言

2006年，中国金融期货交易所正式成立，完善了我国金融市场体系，促进了实体经济的发展. 金融期货市场为金融市场的投资者提供高效的风险管理工具. 因此，针对金融期货市场的稳定性进行相关研究，对整个金融期货市场的发展有着借鉴意义.

迄今为止，学者们从多角度对金融时间序列的波动性有较为充分的研究. Bollerslev［1］提出广义自回归条件异方差（Generalized Auto-Regressive Conditional Heteroscedasticity，GARCH）模型，可以有效拟合具有长期记忆性的异方差函数. Engle 等［2］建立单整广义自回归条件异方差（Integrated GARCH，IGARCH）模型拟合波动冲击的持续性. Robert 等［3］将条件标准差引入均值方程提出GARCH 均值（GARCH-in-mean，GARCH-M）模型. 之后Zakoian［4］提出门限广义自回归条件异方差（Threshold GARCH，TGARCH）模型和Nelson［5］提出指数广义自回归条件异方差（Exponential GARCH，EGARCH）模型，这2种模型用于刻画波动的非对称效应. Yazdanfar［6］研究GARCH模型在波动方面的预测性能，得出GARCH模型对短期的预测效果最好. Laurent等［7］对多元广义自回归条件异方差（multivariate GRARCH，MGARCH）模型的预测性能使用4种统计损失函数进行评估，得出稳定期与不稳定期预测性能有显著差别. Zhe［8］对上证指数进行研究，得出EGARCH模型的拟合优度和预测性能最好. 王俊博［9］以沪深300股指期货为研究对象建立GARCH类模型，得出反映杠杆的波动率模型的预测效果优于没有杠杆效应的波动率模型. 文献［10-11］以已实现波动率为评价衡量标准，采用M-Z 回归和损失函数进行GARCH 类模型预测效果检验. 张胜杰［12］以沪深300指数为研究对象建立GARCH 族模型，得出传统方法选择的样本内最优模型未必取得最优的预测效果. 白娟娟［13］以中国股市为研究对象，6种损失函数为评价指标，评估已实现广义自回归条件异方差（Realized GARCH）模型的预测能力. 邓亚东等［14］以7种损失函数为评价准则，得到Realized GARCH模型具有更优的预测能力. 王新天等［15］对上海原油期货数据拟合GARCH类模型，得出市场中存在较明显的杠杆效应.

目前金融期货的研究相对较少，在衡量模型预测的优劣时，通常有2个标准：一是模型是否能刻画历史数据的特征，拟合波动率能力如何；二是模型能否预测未来的波动率. 本文以M-Z回归和损失函数为评价标准，对沪深300股指期货日收益率序列建立GARCH类模型且对样本内、外预测能力进行评价.

1 研究基础

1.1 模型介绍

1.1.1 GARCH模型

GARCH（m，s）模型中均值方程和波动率方程结构如下：

其中γi表示杠杆效应. 如果γi ＜0 ，则非对称杠杆效应存在.α1+γ1和α1-γ1表示模型对正冲击（at-i ＞0）和负冲击（at-i ＜0）的非对称响应.

1.1.5 TGARCH模型

TGARCH（m，s）模型波动率方程如下：

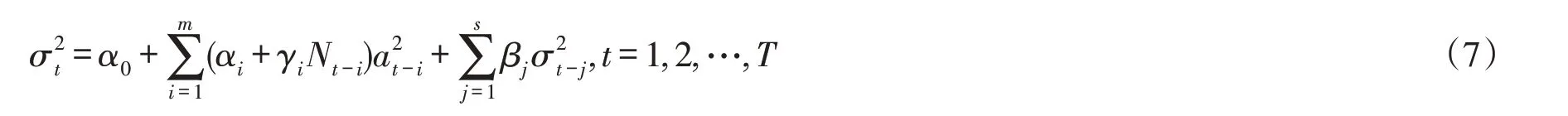
式中t-i和t-j取值为正整数，γi表示杠杆效应. 如果γi ＞0，则非对称杠杆效应存在.Nt-i是关于at-i的指示变量. 好消息（at-i ＞0）时，Nt-i=0，坏消息（at-i ＜0）时，Nt-i=1.

1.2 预测的评估

1.2.1 波动率的预测

以GARCH模型为例，其中ah和σh在时刻h处是已知的. 向前1步预测的条件方差为：

1.2.2 计算已实现波动率

用高频收益数据计算得出的低频收益的波动率就叫做已实现波动率（realized volatility，RV），用来衡量GARCH类模型的预测能力，第t日的已实现波动率计算公式如下：

2 实证分析

2.1 数据选取

选取沪深300股指期货的主力连续合约从2010年4月16日至2021年8月13日的日收盘价数据，共2 756个数据，用于估计模型参数. 对各模型样本内（从2020年8月13日至2021年8月13日，245个交易日）拟合的波动率和样本外（2021年8月14日至2021年8月20日，5个交易日）预测的波动率能力进行评价. 由于只能得到金融资产的观测价格数据，真实波动率不能通过数据直接得出，以日内高频收益数据计算的已实现波动率是真实波动率的无偏估计量［16］，所以用已实现波动率作为真实波动率. 选取从2020年8月13日至2021年8月20日（250个交易日）共12 000个5 min高频收盘价数据，所有高频数据根据式（10）计算出已实现波动率RV，共得到250个数据，用于对GARCH 类模型样本内、外预测能力进行评估.所有数据来源于同花顺，对数据的实证分析结果均由R语言软件编程完成. 本文采取对收盘价Pt取对数再差分，计算得出日收益率序列rt，共得到2 755个收益率数据，相比较收盘价而言，对数差分可以消除数据的异方差性.

2.2 数据统计特征

首先对选取的数据做自相关性、平稳性和自回归条件异方差（ARCH效应）检验. 来判断序列是否适合建立GARCH类模型.

2.2.1 自相关性检验

自相关函数（Autocorrelation Function，ACF）和偏自相关函数（Partial Autocorrelation Fun-ction，PACF）是描述自身在不同时间点的相关程度. 下面对序列rt的自相关性进行分析.

图1中ACF值和PACF值在正负2倍标准差范围以内，则在5%显著性水平下与零没有显著差别. 序列rt中除几个滞后项存在较小的自相关性之外，不存在显著的序列相关. 而对数收益率序列的平方r2t和绝对值 ||rt都是相关序列. 可知序列rt不是相关序列但是存在相依性，并不是独立纯随机序列.GARCH类模型就是在刻画序列的这种相依性.

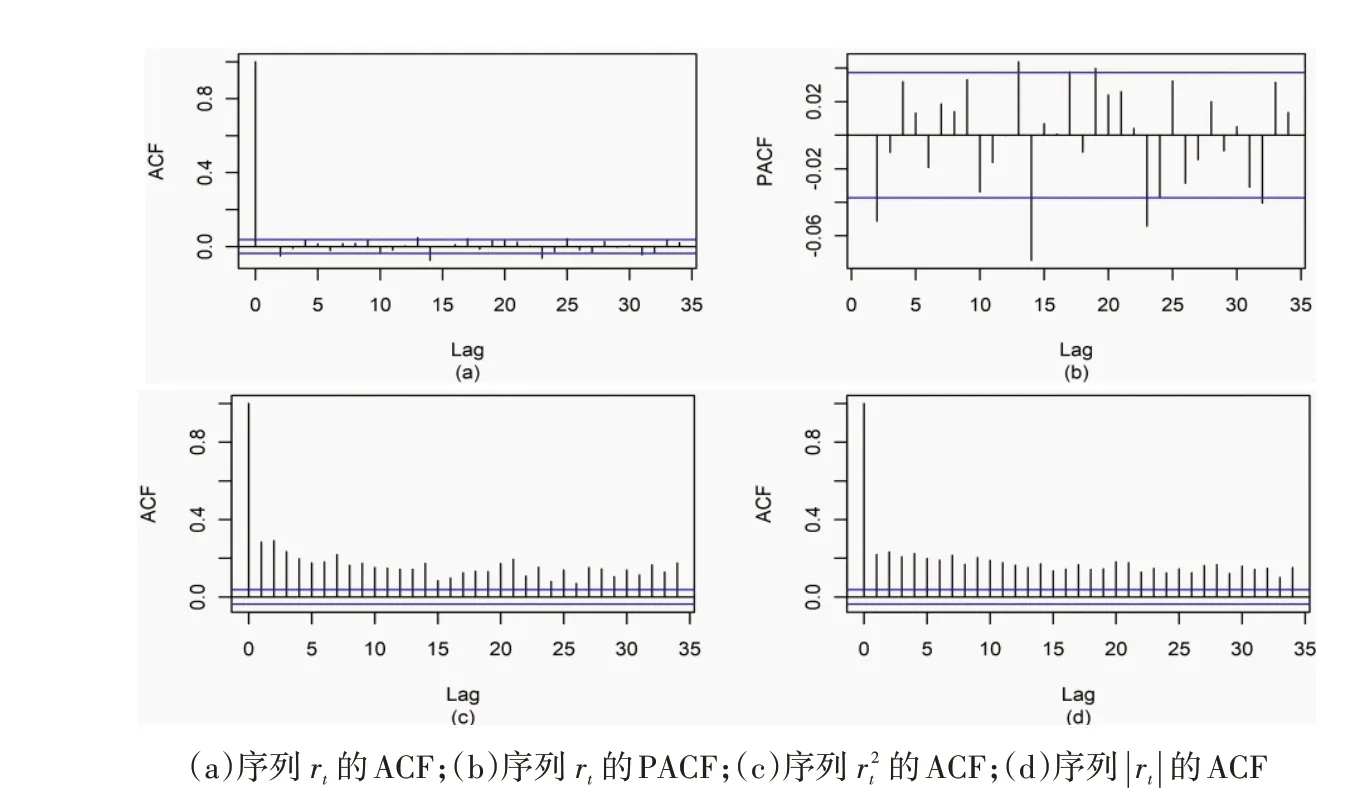
图1 沪深300股指期货日对数收益率序列rt 相关图

2.2.2 平稳性检验和ARCH效应检验

本文用ADF（Augmented Dickey-Fuller ）对序列进行单位根检验. 用拉格朗日乘数（Lagrange Multiplier，LM）对序列进行ARCH效应检验，即ARCH-LM检验.

表1中ADF检验和ARCH-LM检验对应的P值均小于0.01，在1%的显著性水平下序列rt拒绝存在单位根的原假设和拒绝序列不存在ARCH效应的原假设，因此序列为平稳序列且存在ARCH效应. ARCHLM检验滞后阶数的选择并不影响检验结果［17］.

表1 rt 序列检验

2.3 GARCH类模型检验

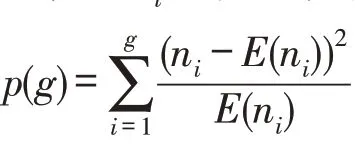
表2中，5个模型的GED分布检验P值均大于0.05，所以在5%的显著性水平下，5个模型GED分布均不能拒绝符合标准化残差的经验分布的原假设，因此最优为GED分布. 而TGARCH模型中Skewed-students-t分布和GED分布P值均大于0.05，所以在5%的显著性水平上，TGARCH模型中这两个分布都可以接受，GED分布更优.

表2 GARCH类模型的标准化残差经验分布和理论分布的泊松拟合优度检验

根据以上结果，拟合标准化残差服从GED分布的GARCH类模型，见表3. 首先用Ljung-Box Q 统计量检验标准化残差的自相关性，此检验原假设为序列不相关. 若标准化残差序列{εt}和序列{ε2t}是不具有自相关的序列，则分别说明均值方程和波动率方程拟合充分. {εt}的ARCH-LM检验，用于检验模型是否消除序列的异方差效应.

表3 GED分布下的GARCH类模型拟合结果及检验

表3中GA（1，1）、GA（1，1）-M、IGA（1，1）模型α1和β1表示外部的冲击（新冲击）和内部的冲击（旧冲击）对波动率的影响情况. 模型计算结果说明在沪深300股指期货市场的波动性中受新冲击要小于旧冲击的影响. 自由度（Shape）估计值均小于2，说明标准化残差具有厚尾特征. 其中IGA（1，1）模型中β1=1-α1，所以除了IGA（1，1）模型的参数β1没有T统计值外，GA（1，1）、GA（1，1）-M、IGA（1，1）这3个模型的其余参数都在5%显著水平上显著. EGARCH模型和TGARCH模型非对称项参数γ1不显著，则认为rt序列不存在波动的非对称效应.

5个模型中εt的Ljung-Box Q（5）检验、ε2t的Ljung-Box Q（5）检验以及εt的ARCH效应检验，显示模型的均值方程、波动率方程拟合充分以及残差不存在ARCH效应. 因此5个模型拟合是成功的.

2.4 GARCH类模型的预测评估

为全面比较模型样本内预测的好坏，对以上5个模型拟合的波动率进行预测评估. 根据M-Z回归式（11）和损失函数式（12）、（13）和（14），计算结果见表4.

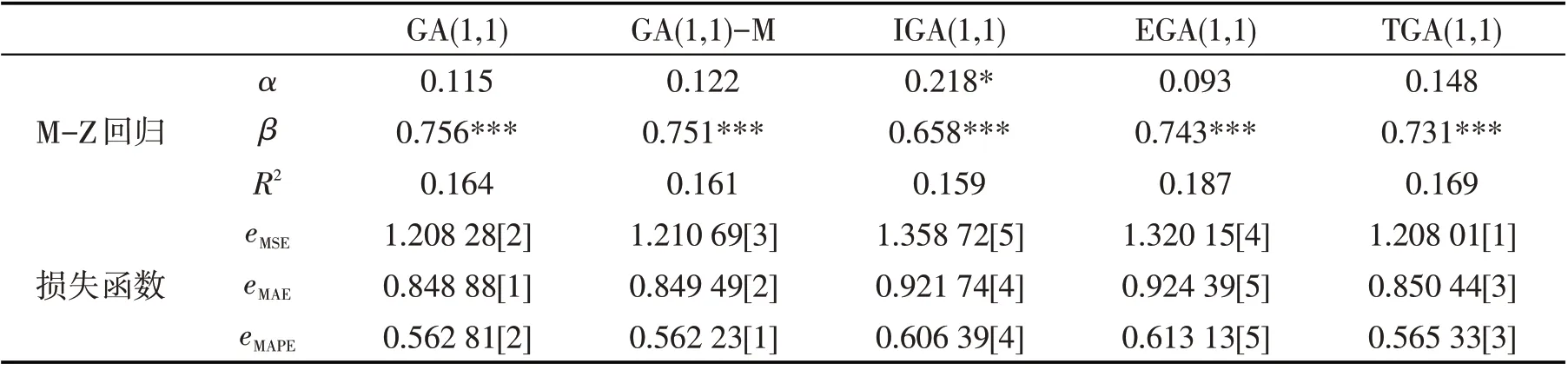
表4 GARCH类模型的样本内预测评估

表4中M-Z回归结果，拟合优度R2均较低. 但大部分的金融时间序列实证表明R2普遍小于0.1，所以R2在0.1以上认为拟合比较好.β的系数检验均显著不为零，根据β接近1且α不显著，预测效果最好的为GARCH（1，1）模型. 从拟合优度来看EGARCH（1，1）模型最好. 从损失函数来看，GARCH（1，1）模型各损失函数值均较小，其预测能力是最好的. 综合来看，样本内预测能力最好的为GARCH（1，1）模型.

接下来对5个模型分别根据式（8）和（9）进行向前1步至5步预测，进行样本外预测评估. 经过计算向前1步至5步的预测表现一致，因此只列出向前预测5步的计算结果，见表5.

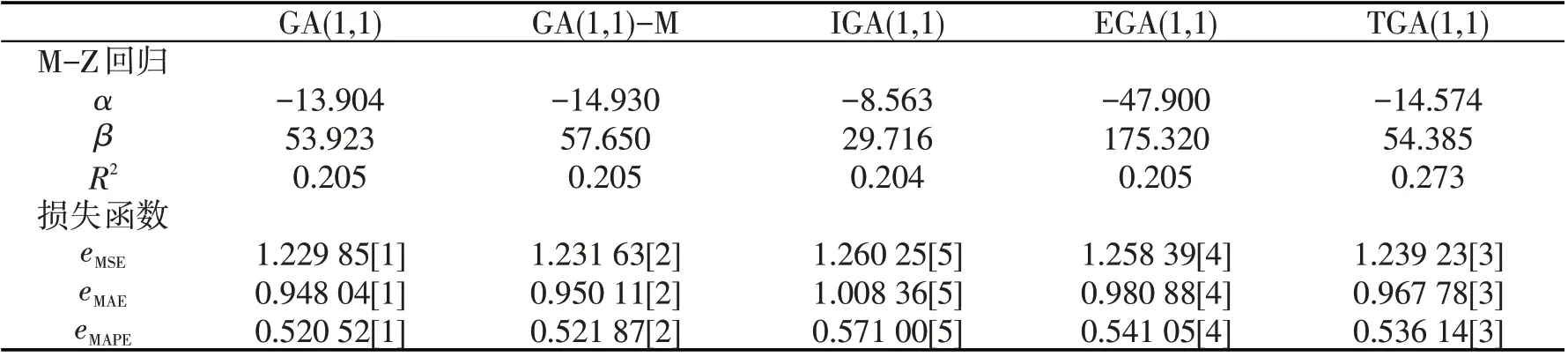
表5 GARCH类模型的样本外预测评估

表5中M-Z回归结果，α和β的系数检验均不显著而且β系数值远大于1，回归结果较差，依据M-Z回归不能评价模型预测好坏. 从损失函数来看，GARCH（1，1）模型各损失函数值均较小，其预测能力是最好的. 对于沪深300股指期货日对数收益率来说，不管样本内还是样本外最好的预测模型为标准残差服从GED分布的GARCH（1，1）模型. 由GARCH（1，1）模型预测效果图2和图3可以看出，即便是预测能力最强的GARCH（1，1）模型，也难以预测极端损失.

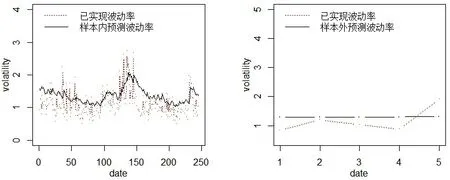
图2 已实现波动率与样本内预测波动率

3 结论

文章在高斯分布、学生-t分布、偏斜-学生-t分布、广义误差分布4 个残差分布假定下分别拟合GARCH、GARCH-M、IGARCH、EGARCH、TGARCH 5个模型. 首先经过泊松拟合优度检验得出广义误差分布是最优的残差假定分布，其次建立GED分布下的GARCH类模型，最后对模型样本内、外预测效果以已实现波动率为衡量标准通过M -Z回归和损失函数进行检验. 结果表明，有GED分布的GARCH（1，1）模型是样本内和样本外预测沪深300股指期货日收益率的波动率最佳模型.