既有跨海桥梁增设风障方案分析

■张 杰

（福建省交通规划设计院有限公司，福州 350004）

福建省平潭海峡大桥位于福建省东部， 起于福清市小山东半岛， 横跨福清市小山东至平潭岛之间的海坛海峡，终点与金井湾大道相接，是平潭岛第一座对外公路交通通道。大桥由双幅桥组成，其中左幅桥于2010 年11 月建成通车，右幅桥于2014 年6 月建成通车，两幅桥组成双向六车道高速公路。

平潭海峡大桥所处的区域受季风和热带气旋影响显著，为台风登陆和影响区，大风频发，桥址区100 年重现期设计风速43.3 m/s， 基于平潭气象站1971-2012 年间的每日最大10 min 平均风速数据，并结合桥位地形风环境数值模拟结果，得出了平潭海峡大桥主桥最高桥面位置每日最大10 min 平均风速不同分级的统计，风速大于等于8 级风的天数达到33.1 d/年[1]，大风对桥梁运营安全的不利影响显著。 目前大桥没有专门提高风天线路通行安全的结构措施，大桥运营期间，当桥位风速达到一定数值时，常出现车辆发飘、行驶偏向等问题，针对桥面8 级及以上大风时， 也只能被动采用对通行安全保障效果不佳的限速和封桥措施。 因而，采取设置于桥面的风障结构，从根本上提高大桥风天的通行安全，提高跨海通道的运营效率，无疑是该桥运营管理必须要解决的问题。

本研究以平潭海峡大桥为依托，研究了大桥桥面风速分布规律、桥面等效风速、风障实施效果、主梁断面的气动力三分力系数，并对增设风障后的主桥及引桥结构进行了验算，可为同类桥梁设计提供参考和借鉴。

1 工程概况

桥位处海坛海峡海面宽约3.5 km，大桥总长3 510 m，其中主桥采用（100+2×180+100）m 预应力混凝土连续刚构桥， 两侧引桥采用50 m 预应力混凝土连续箱梁，大桥总体布置见图1。大桥采用双幅布置，单幅桥宽17 m，两幅间净距25 m，共6 个车行道和2 个停车带，主桥跨中断面见图2。

图1 大桥主桥及部分引桥总体布置图

图2 主桥跨中断面示意图

主要技术标准：设计速度100 km/h；设计荷载公路I 级；设计基本风速43.3 m/s，全桥桥面最高点处（高程51 m）换算设计基准风速52.6 m/s。

2 风障方案设计

风障采用与混凝土护栏相结合的设置形式，风障钢立柱锚固于护栏上，钢立柱纵桥向间距约1.6 m，竖向设置4 条风障条，风障+护栏总高度3.5 m。 风障挡风率考虑40%、50%及60% 3 种情况， 综合考虑风障所提供的桥面行车风环境改善效果，与尽可能减少风障设置增加主梁风荷载对结构的不利影响，通过采用本研究方法分析比较后，推荐采用挡风率40%的风障结构方案，风障布置见图3、效果图见图4。

图3 风障方案示意图）

图4 风障效果图

3 桥面风环境分析

已有研究表明，采用数值风洞技术模拟分析桥面风环境的结果与风洞试验结果相近，数值模拟方法是有效的[2]。 因此，采用数值风洞技术对平潭海峡大桥代表性位置桥面风环境进行了研究，提取等效桥面风速及其影响系数等参数，以分析桥面风速分布的规律。

3.1 计算模型及网格划分

首先按照设计图纸的结构尺寸图，建立主梁的几何模型，然后进行空间区域的网格划分。 几何模型主要包括主梁、护栏、风障等构件。 平潭大桥主桥共考虑选取4 个主要典型断面进行风环境数值模拟研究，典型断面纵桥向位置见图5，断面网格划分见图6。

图5 典型断面纵桥向位置示意图

图6 网格划分示意图

3.2 计算方法及边界条件设置

主梁周围流场的数值模拟是以Navier-Stokes方程（绕流风的连续性方程及动量守恒方程）为基本控制方程， 采用离散化的数值模拟方法求解流场。 在Navier-Stokes 方程求解中，采用基于时间平均的雷诺均值Navier-Stokes 方程（RANS）模型中使用最广泛的Realizablek-ε 双方程湍流模型。

计算域边界至梁体边界的距离参考文献[3]确定。流体入口边界条件采用均匀来流10 m/s 的速度进口；出口边界条件为压力出口；无滑移固壁边界条件：桥面、风障、护栏等。

3.3 桥面行车高度风环境分析

在计算区域设置一定的入口速度，通过数值求解可获得主梁区域的流场分布，从而可评估主梁区域的风环境。 为研究空间风速的变化，引入速度系数变量α 来分析流场，该变量定义为：

上式：α 为速度系数，vmean为研究空间某点的平均速度，vin为入口风速。

通过该系数的大小就可判断桥面空间区域某点的风速相对大小， 系数越大表示该点风速越大，系数越小表示该点风速越小，系数大于1 表示该点风速大于来流风速，系数小于1 表示该点风速小于来流风速。

横桥向取各车道中心线桥面以上10 m 范围为风速监测位置，按照风速来流方向分别定义为车道1～8，其中上游迎风侧车道1～4，下游背风侧车道5～8，见图7。

图7 车道监视位置示意图

平潭大桥主桥共选取了4 个断面进行了风环境数值模拟研究，以下给出纵桥向位置4 研究结果。

（1）不设置风障工况下，双幅桥面周围流场分布、 各车道风剖面及桥面风速分布曲线见图8～10。可知两幅桥的风环境分布规律有所不同。 对于迎风侧主梁，由于护栏的阻挡作用，护栏后的风速较低，并在护栏高度范围形成回流，但在护栏高度以上，风速迅速增大，车道1 在高度2.3 m 时风速系数大于1，高度2.8 m 时风速系数达到最大值1.28，车道2～4 在3～4 m 高度范围风速系数分别达到最大值1.31。 对于背风侧主梁，由于迎风侧主梁及护栏的阻拦，车道5～8 风速系数均小于1。

图8 桥面流场显示（无风障）

图9 各车道风剖面图（无风障）

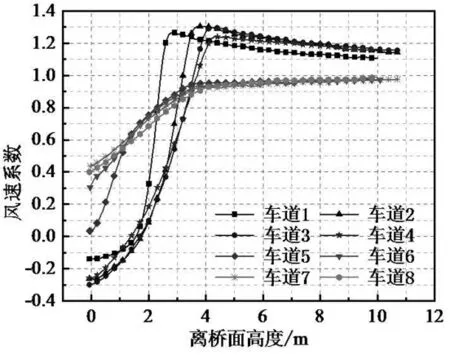
图10 各车道风速分布曲线（无风障）

（2）设置风障工况下，双幅桥面周围流场分布、各车道风剖面及桥面风速分布曲线见图11～13。可以看出，风障的设置使得风速达到或超过来流风速的位置提高，其中车道1 提高到4.3 m 以上，车道2～4 提高到5.2 m 以上，大大改善了行车高度范围桥面风环境。

图11 桥面流场显示（带风障）

图12 各车道风剖面图（带风障）

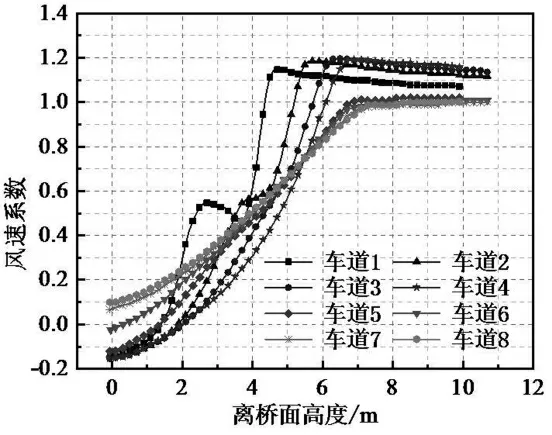
图13 各车道风速分布曲线（带风障）

3.4 等效桥面风速及影响系数

由上可知，当侧风经过桥面时，由于主梁、护栏及风障等附属结构的影响，均匀的侧向来流风速在桥面形成一定厚度的边界层，作用于车辆的风速将不同于均匀的来流风速， 为量化评价桥面风环境，根据侧向气动力等效原则定义等效桥面风速如下：

式中zr表示汽车所处的高度范围，一般中型客车、大型客车和大型厢式货车高度范围选为5.0 m。

将桥面行车高度范围等效风速与外侧来流风速的比值定义为风速影响系数λs，该值越小说明桥面风环境越安全。

式中U∞为侧向来流风速。

根据桥面各车道的风剖面可计算出各车道5.0 m 高度范围的等效风速及风速影响系数， 其中主桥纵桥向位置4 各车道设置风障前后的风速影响系数、等效风速对比见表1、图14。 从表1 不同车道影响系数对比可知：（1）不设置风障工况下，上、下游桥面8 个车道的桥面风速影响系数均小于1，其中上游4 个车道的桥面风速影响系数从车道1至车道4 递减， 即在上游来流风速情况下， 车道1的侧向风速最大；下游车道5 至下游车道8 的桥面风速影响系数基本相当。 （2）设置风障工况下，各车道桥面风速影响系数分布规律同不设置风障工况，但各车道桥面风速影响系数显著减少，其中上游车道1 桥面风速影响系数仍为8 个车道最大值，但比未设置风障情况约减少37%。 因此，风障的减风效果十分显著。

表1 主桥位置4 桥面不同行车道风速影响系数

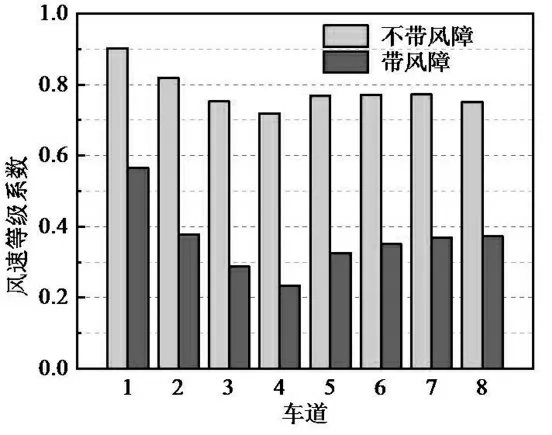
图14 主桥位置4 等效风速对比

4 风障实施效果评价

基于已有研究和桥梁风天运营管理的经验，一般桥面风速达到17.2 m/s（8 级风）时，汽车就会出现侧风影响的安全问题，如侧向偏移；当风速继续加大，则会出现侧滑，甚至是侧向倾覆。 因此本工程进行风致行车安全评估时认为：桥面行车高度范围内等效风速达到8 级风（17.2 m/s）时要对大桥进行风天行车安全控制（如对车辆进行限速等控制措施）；当桥面行车高度范围内风速达到10 级风（24.5 m/s）时要封闭交通。 安全评估时风速取实际影响车辆侧风安全的瞬时风速，该数值根据大桥最高桥面位置每日最大10 min 平均风速换算得到，二者换算系数约为1.5。

基于本研究成果，并结合统计分析的桥位瞬时风速概率分布，采用风天桥面行车安全概率性评价方法，对大桥全线17.2 m/s 限速和24.5 m/s 封闭的双目标控制风速下行车安全进行分析。 设置风障前后，经过高度修正和桥面风速影响系数修正的主桥桥面最高位置的瞬时风速概率分布见表2、表3。

（1）由表2 可知，未设置风障时主桥桥面最高位置迎风侧车道1 瞬时风速概率分布情况。 未设置风障时，大桥实际需要进行交通控制的大风天数约为92.2 d/年（ 8 级风以上），其中需要封桥的大风天数约为10.9 d/年（10 级风及以上）。

（2）由表3 可知，增设挡风率40%风障后主桥桥面最高位置迎风侧车道1 瞬时风速概率分布情况。 增设风障后，大桥实际需要进行交通控制的大风天数总计约为13.9 d/年（8 级风及以上），其中需要封桥的大风天数仅为0.9 d/年（ 10 级风及以上）。

表3 桥面最高位置迎风侧车道1 瞬时风速概率分布（增设挡风率40%风障）

（3）风障设置前后的交通控制天数对比分析表明：风障的合理布置，可以提高大桥风天的通行效率，显著提高了风天行车安全水平。

5 主梁风荷载参数分析

采用流体动力学分析方法（CFD）分别计算了平潭海峡大桥主桥主梁成桥状态4 个断面的气动阻力系数、升力系数和扭矩系数三个分量，截面位置见图3，主梁断面三分力作用点及其方向见图15。

图15 主梁断面三分力作用点及其方向示意图

由于大桥各位置桥面宽度保持不变，梁高连续变化。 为结果处理的方便，因此计算结果取桥面宽度为参考长度，参考坐标轴为风轴坐标。 其中静气动力定义为：

阻力系数：CD=FD/qwB；

升力系数：CL=FL/qwB；

扭矩系数：CM=FM/qwB。

式中，qw=（1/2）ρVw2为来流动压；ρ 和Vw分别为空气密度和来流速度；CD、CL、CM分别为每延米阻力、升力、扭矩；B 为主梁宽度，取17 m。

根据CFD 分析得到设置风障前后主桥不同位置处断面的静气动力系数，见表4、表5。

表4 主桥不同位置截面静气动系数（无风障）

表5 主桥不同位置截面静气动系数（增设挡风率40%风障）

由表4、5 可知，由于风障的设置增加了结构阻风面积，加大了结构静气动力系数，从而增大风荷载对桥梁结构尤其是下部结构的不利影响。 因此，考虑风荷载参与的荷载组合条件下的受力验算是既有桥梁增设风障的一个关键问题。

6 增设风障后的结构验算

6.1 有限元模型建立

采用有限元程序Midas Civil 建立主桥空间模型（图16）。 其中，主梁、桥墩、承台及桩基均采用空间梁单元，全桥共2 119 个单元。 桩底约束采用固定约束，土层采用节点弹性支承，墩梁之间采用刚性连接。

图16 平潭大桥主桥Midas 模型

6.2 荷载取值

恒载及活载按设计图纸及《公路桥涵设计通用规范》[4]进行取值，波流力值参考相关专题资料。

风荷载：百年一遇基本风速Vd=43.3 m/s，场地类型A 类地貌，粗糙度指数取0.12；常遇风荷载取桥面高度处风速Vd=25.0 m/s。

6.3 承载力验算结果

根据结构受力特点，本研究着重分析验算了主桥43#～45# 薄壁墩和桩基的内力以及相应的强度和抗裂性。 结构验算时，考虑可能同时出现的作用按照通用规范要求进行了最不利效应组合，按《公路钢筋混凝土及预应力混凝土桥涵设计规范》[5]进行了承载能力极限状态、 正常使用极限状态相关验算。

验算结果表明：横桥向和顺桥向风参与组合的各个工况下，就双薄壁墩而言，墩底截面为最不利截面。在各个工况作用下，43#～45#薄壁墩及桩基经验算均满足结构强度和抗裂性要求。 列出43#主墩最不利工况下墩底截面及桩基截面抗弯承载力验算结果，见表6、表7。

表6 43# 墩底截面抗弯承载能力验算

表7 43# 墩最不利桩基截面抗弯承载能力验算

7 结论

本研究结果得出以下结论：（1）风障的合理布置，可以大大改善桥面行车风环境，显著提高大桥风天行车安全水平及风天的通行效率。（2）风障的设置增加了结构阻风面积， 增大了桥梁结构所承受的风荷载，对桥梁结构尤其是下部结构产生不利影响。考虑风荷载参与的各种荷载组合条件下的受力验算是既有桥梁增设风障的一个关键问题。（3）经结构验算，采用推荐的风障方案，增设风障后平潭海峡大桥主桥及引桥下部结构受力验算满足规范要求。