带有非奇异核分数阶差分方程的比较原理及解的不确定性分布

陈雨婷, 李晓艳, 王雪芹

(安徽大学数学科学学院，合肥 230601)

0 引言

分数阶微积分起源于1695 年左右，由于其应用的广泛，分数阶微积分和分数阶微分方程得到了迅速发展，如热系统、动力系统、物理学等应用领域[1–3]。因此，受到了学者们的广泛关注。随着分数微分方程理论的发展，文献[4—7]对分数阶差分方程进行了更深入的研究。一些学者致力于分数阶差分方程的应用，文献[8—9]研究了分数阶差分方程的初值问题，文献[10—11]分别讨论了不同类型分数阶差分方程的稳定性问题。在文献[12]中，作者研究了分数阶差分方程正解的存在性。最近，Abdeljawad 和Baleanu[13]提出了具有Mittag-Leffler 核的ABR 型分数阶差分算子的定义。之后，ABR 型分数阶差分算子的许多基本性质和结果被给出，例如，文献[14]研究了离散Mittag-Leffler 核的分数阶差分方程的初值问题；文献[15]讨论了ABC 型分数阶差分算子的单调性和均值定理。此外，在文献[16]中，Abdeljawad 进一步提出了具有Mittag-Leffler 核的高阶分数阶差分算子。

另一方面，学者们研究了不同类型方程的比较原理，例如，文献[17]讨论了Riemann-Liouville 型分数阶微分方程的比较定理；Denton 和Vatsala[18]以积分不等式的形式给出了此定理；文献[19]研究了分数阶微分方程的比较定理；文献[20—21]推导出了分数阶微分方程的比较定理。此外，文献[22]给出了以下方程的比较定理

Liu 在文献[23—24]中分别提出了不确定性理论和不确定性微分方程的概念，它们通常用于描述随时间演化的不确定性动力系统，学者们无论是在理论，还是应用中都讨论了不确定性微分方程[25–28]。近年来，文献[29]通过比较原理提供了一种求解不确定分数微分方程的数值方法，并在文献[30]中引入了不确定性分数阶微分方程的定义。此外，文献[31]提出了一种Riemann-Liouville 型分数阶方程的比较定理，并应用此定理建立了不确定性分数阶微分方程和分数阶微分方程之间的关系。因此，在以往结论的启发下，本文的目的是利用ABR 型分数差分方程的比较定理给出ABR 型分数阶差分方程和其对应的不确定性分数阶差分方程之间的联系。

本文结构如下：第1 节介绍了分数阶微积分和ABR 型分数阶差分的基本定义；第2 节给出了ABR 型分数阶差分方程的比较定理；基于第2 节的比较定理，在第3 节建立了ABR 型不确定性分数阶差分方程的解与ABR 型分数阶差分方程的解之间的关系，并举例阐述了定理的正确性；第4 节给出了具有对称的不确定性变量的ABR 型不确定性分数阶差分方程解的不确定性分布。

1 预备知识

本节将介绍在整篇论文中用到的离散型分数阶积分的一些基本定义和结论。另外，在本文中我们记：Na={a,a+1,···}，其中a ∈R, aN={··· ,b −1,b}，其中b ∈R。

定义1(离散型分数阶和分)[13]设ρ(t) =t −1 为向后跳跃算子，0<β< 1，函数f:Na →R，则离散型β阶和分的定义如下

定义2(双参数离散的Mittag-Leffler 函数)[13]对于λ ∈R,|λ|< 1，β,γ,z ∈C，Re(β)>0，双参数离散的Mittag-Leffler 函数定义如下

引理1 离散的Mittag-Leffler 函数的分数阶和分和差分满足：

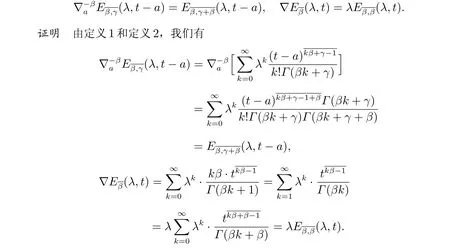
更多关于离散的Mittag-Leffler 函数的性质可以参考文献[13]。

2 ABR 型分数阶差分方程的比较原理

考虑下列给出的ABR 型分数阶差分方程

本节将运用反证法来给出ABR 型分数阶差分方程的比较原理。

定理2 设f(t,y)和g(t,y)是定义在Na×R 上的实值函数，函数g是连续的，关于y满足利普希茨条件(利普希茨常数为Lg)，且满足y1(t)和y2(t)分别是下列方程的解

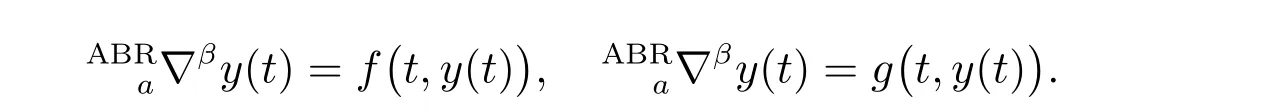
(a) 如果f(t,y)≤g(t,y)，则y1(t)≤y2(t), t ∈Na；

(b) 如果f(t,y)>g(t,y)，则y1(t)>y2(t), t ∈Na。

证明 (a) 假设y1(t)≤y2(t)不成立，那么至少存在一点t0∈Na，使得y1(t0)>y2(t0)。定义{}

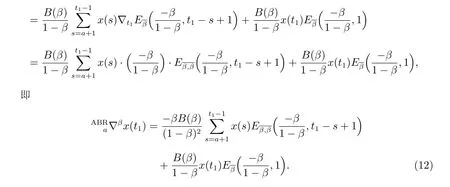
另一方面，由定理条件知f(t,y)≤g(t,y)，函数g是连续的且关于y满足利普希茨条件，利普希茨常数Lg满足

因此，我们有x(t1)<0，与(10)式矛盾，假设不成立，定理2 的(a)部分证毕。

(b)与(a)的证明过程类似，假设y1(t)>y2(t)不成立，则至少存在一点t0∈Na，使得y1(t0)≤y2(t0)。记

另一方面，由定理条件可知f(t,y)>g(t,y)，函数g是连续的且关于y满足利普希茨条件，利普希茨常数Lg满足

3 ABR 型不确定性分数阶差分方程的α-路径

本节定义不确定性分数阶差分方程的对称不确定性变量和α-路径，并给出ABR 型不确定性分数阶差分方程的解和对应的分数阶差分方程的解之间的联系，然后结合第2 节中的比较定理，我们得出具有对称不确定变量的不确定性分数阶差分方程的解及其α-路径之间的联系。首先，本节将给出有关不确定性理论的一些基本知识。

设Γ是一个非空集合，称Γ中一些子集所构成的集合L为σ代数，称每个σ代数L中的元素Λ为事件，称集函数M为不确定性测度，如果它满足以下公理。

公理1(正则性)[23]对于所有的集合Γ, M{Γ}=1；

公理2(单调性)[23]M{Λ1}≤M{Λ2}, Λ1⊂Λ2；

公理3(自反性)[23]对于任意的Λ, M{Γ}+M{Γc}=1；

公理4(次可列可加性)[23]对于每个可数列Λi，我们有

定义5[23]不确定性变量ξ的不确定性分布Φ:R−→[0,1]的定义为

定义6[23]我们称不确定性分布Φ(x)是均匀的，若它关于x是连续的、严格递增的，0<Φ(x)<1，且

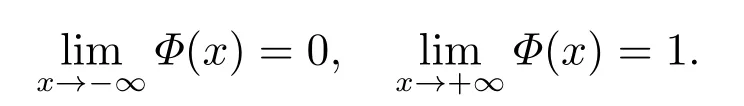
定义7[31]设ξ是具有均匀的不确定性分布Ψ(x)的不确定性变量，若Ψ(x)+Ψ(−x)=1，则称ξ是对称的。

定义8[31]若不确定性变量ξ的不确定性分布Φ(x)是均匀的，则称函数Ψ−1(α)为ξ的不确定性逆分布。

当N(t,x)<0 时，我们有

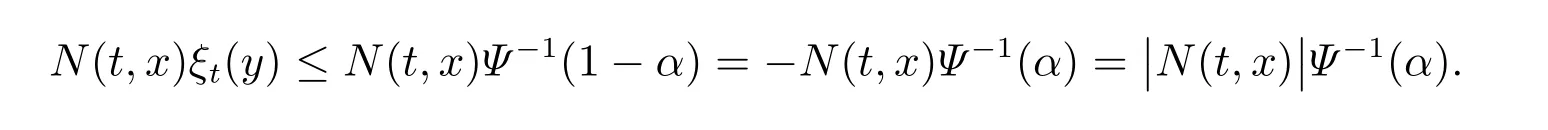
因此，对任意的y ∈V+∩V −，都有

利用定理2，我们得到对任意的t ∈Na ∩[0,T]，都有Xt(y)≤Xαt成立。因此

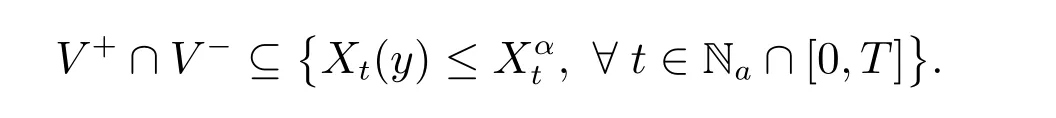
根据单调原理，我们有

另一方面，令

重复上述步骤，对任意的y ∈U+∩U−，有

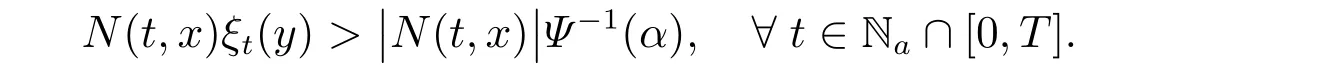
类似地，我们可以推断出

因为

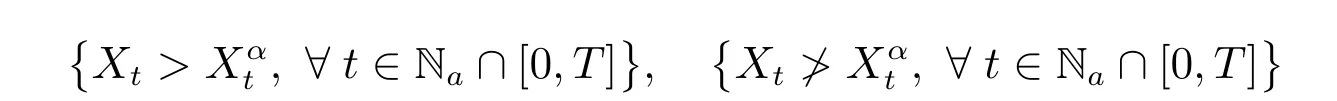
是对立事件，所以

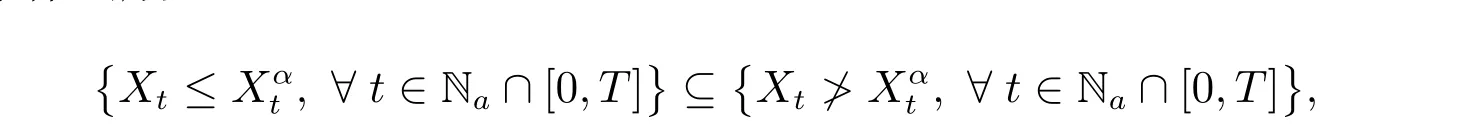
根据单调原理可得

又因为

即

因此，由(23)∼(25)式，我们可以得出下列等式成立：

4 ABR 型不确定性分数阶差分方程解的不确定性逆分布

关于x是利普希茨连续的，利普希茨常数为Lg且满足

且利普希茨常数为

则函数

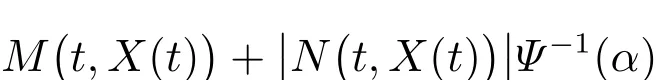
关于x是利普希茨连续的。因此，根据存在唯一性定理可得方程(27)有唯一解。

由定理4，我们得到方程

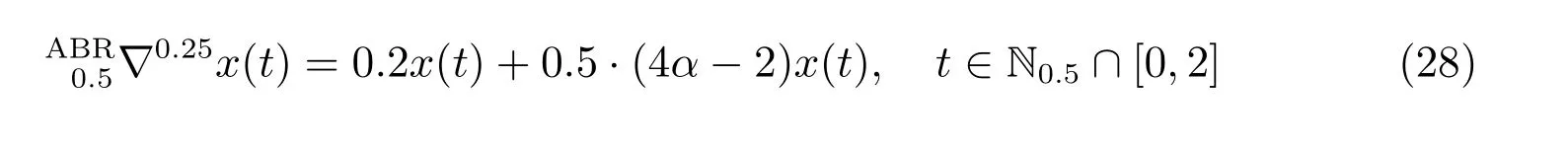
有唯一解

5 结论

本文主要介绍了ABR 型分数阶差分方程的比较原理，并应用比较原理给出了ABR 型分数阶差分方程的解与具有对称不确定性变量的ABR 型不确定性分数阶差分方程之间的联系。通过引入α-路径的概念，本文证明了ABR 型不确定性分数阶差分方程解的逆分布就是解的α-路径。此外，还通过例子来阐述结果的正确性。我们未来可能的工作是讨论ABR 型不确定性分数阶差分方程的其它不确定性变量，并研究相关文献中提出的ABR 型不确定性分数阶差分方程的数值解。