基于球体堆积模型设计的多胞薄壁结构抗冲击性能研究
胡敬坤,徐 鹏,范志强,谭晓丽,李耀宙
(中北大学 航空宇航院,山西 太原 030051)
多孔材料具有轻质、高耗散力、优异的吸声、耐热性和高冲击能量吸收的特性,在20世纪80年代末迅速兴起,并且广泛应用于在航空航天、军事和民用等领域[1]. 多孔材料根据其微观构型,可以分为两种类型[2],一种是以蜂窝为代表的二维多孔材料,一种是以泡沫铝、空心球结构为代表的三维多孔材料. 空心球结构作为一种典型的高质量多孔材料受到了学者们的广泛研究. 戴美玲等[3]研究了一种新型空心球结构的压缩力学性能,设计了一种新型的穿孔空心球结构,与传统结构对比后发现其力学性能比壁厚对孔径的变化更为敏感. Sonti等[4]采用不同的颗粒尺寸及粉末成型的方法制作了三种不同体积分数的空心球结构,通过准静态压缩试验发现,颗粒尺寸和体积分数对材料的峰值应力有着显著的影响,其能量吸收效率随着体积分数的增加而降低. 宋金良等[5]研究了孔隙分布对金属空心球准静态压缩特性的影响,发现空心球的压缩过程分为弹性变形、屈曲和屈服变形、球壁坍塌变形和致密化四个阶段,并得出了孔隙率及其分布对金属空心球变形破坏模式的影响规律.
上述研究主要集中在对空心球本身的力学性能上,并未深入研究空心球结构与三维点阵结构相结合的问题. 三维点阵结构具有与传统结构不同的微结构与高孔隙率,且其具备轻质高强、抗爆炸抗冲击、高效散热隔热、吸收电磁波及声音等优异性能[6],因此,将空心球结构与三维点阵结构相结合也就成为一种新的思路. 近年来,随着3D打印技术的发展,许多点阵结构制备的复杂程度和成本大大降低,使得三维点阵结构和其他复杂构型的结合能够实现. 张璠等[7]对三维点阵结构的力学性能进行计算分析,并利用有限元软件对其实际应用进行了仿真计算,证明三维点阵结构在轻量化设计中有着显著的优势. 吴鹤翔等[8]通过对具有密度梯度的三维金属空心球力学性能的分析,说明了可以通过改变其点阵排布类型来达到控制应力峰值和提高能量吸收的目的. BIAN等[9]对不同材料和制备方法的体心立方点阵结构进行了准静态压缩试验,并进行了有限元仿真对比,发现使用AlSi10Mg、PLA和PA12材料制作的体心立方点阵结构,其致密化应变都在0.7左右,这为研究点阵结构提供了一种可行的方案. HASANAIN等[10]分析了体心立方点阵结构的支柱长度和角度对其力学响应的影响,发现其最高比吸能和比刚度是由小角度变高度支柱所决定的.
本文基于体心堆积(BCC)模型来构建球壳类多胞结构,通过引入肋板来提高球壳连接管抗弯刚度和稳定性,并且分析了不同构型与结构能量吸收之间的关系,通过合适的结构设计来改善结构的变形模式以提高吸能效率,以期为新型吸能结构的设计提供了一种全新的思路.
1 几何模型和数值模拟
1.1 几何模型
球壳类多胞薄壁结构是将空心球壳按照一定的排列模式连接起来,球体上的孔均匀地分布在球体上,用作与其他空心球壳连接的连接颈,不同的排列模式其开孔的大小和开孔方向都不相同,三种排列模式(简单立方(SC),体心立方(BCC)和面心立方(FCC))有三种不同的空心球壳结构. 其中,体心立方结构因其拓扑类型简单,可靠性好,压缩失效形式单一等优点,而成为点阵结构的首选[11].
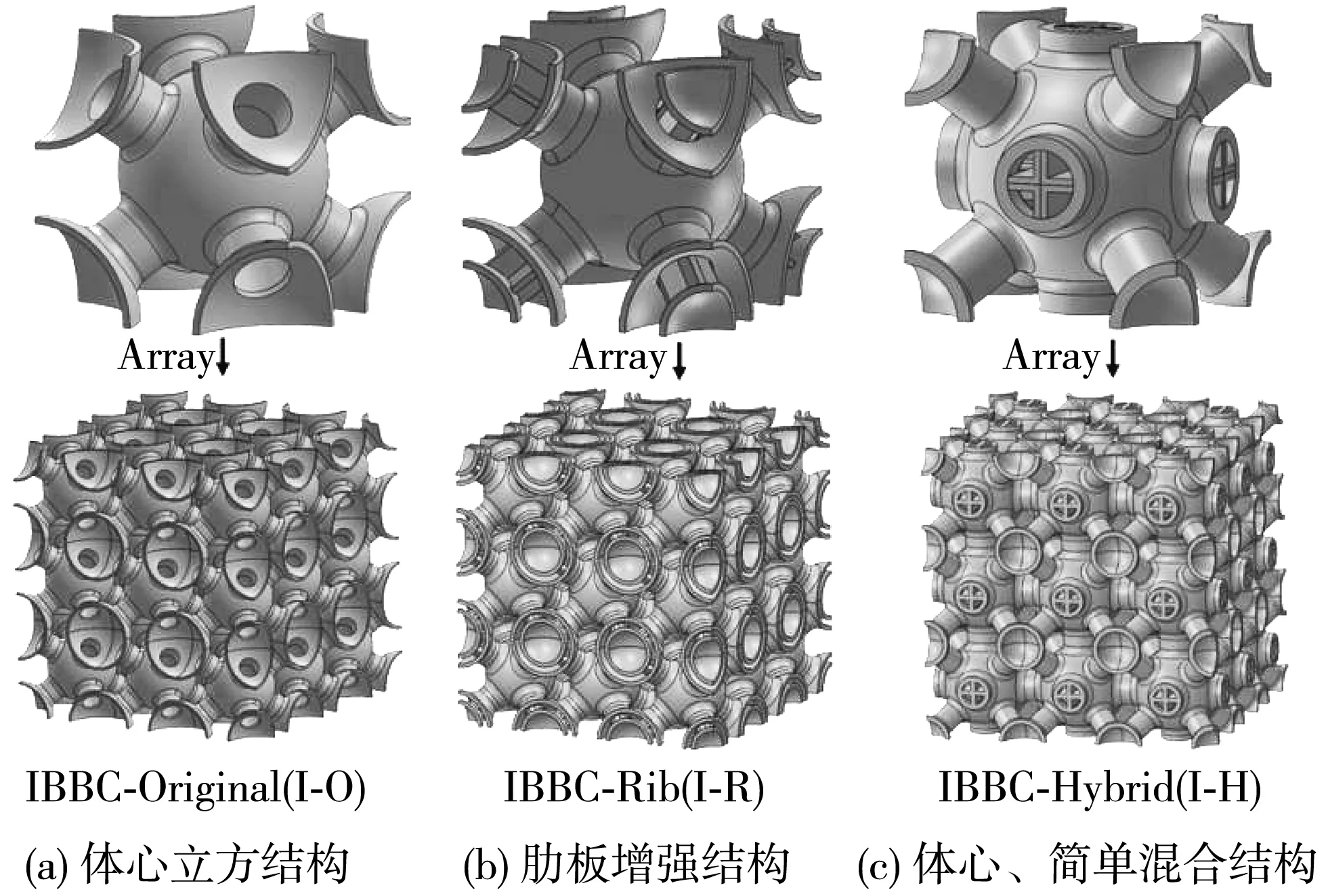
图1 三种模式的空心球结构 Fig.1 Three modes of hollow sphere structure
图1 为三种仿体心立方(Imitated Body-centered Cubic)的空心球壳结构. 该结构中采用理想的柱状几何体来简化并模拟球体之间的连接结构,同时,在柱状几何体中添加连接肋板来增强其连接效果. 为了减少连接结构与两个球体之间的应力集中效应,在连接处设置半径为1 mm的圆角.
图2 为I-R和I-H的剖面图,其中L为单胞结构边长,D为外层球壳(Outer ball)直径,d为内层球壳(Inner ball)直径,t为结构的壁厚,h为连接管(Connecting tube)的长度,连接管中有连接肋板(Connecting rib),θ为连接管与水平面的夹角. 在多孔固体材料中,相对密度是体现多孔结构力学性能的一个重要的参数,因为整体三维点阵结构使用一种材料进行3D打印,故其相对密度表达式为
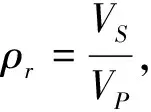
(1)
式中:VS为实体材料整体的体积;VP为对应的三维多孔点阵结构的总体积. 根据式(1)可以得出该结构的孔隙率为

(2)
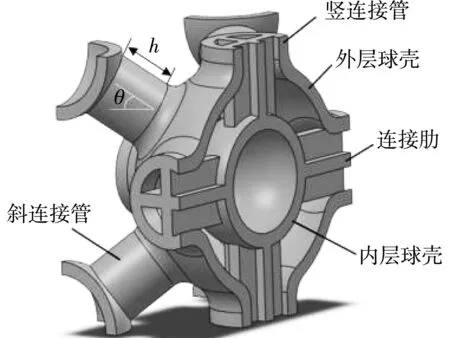
(a) 肋板增强结构剖面图
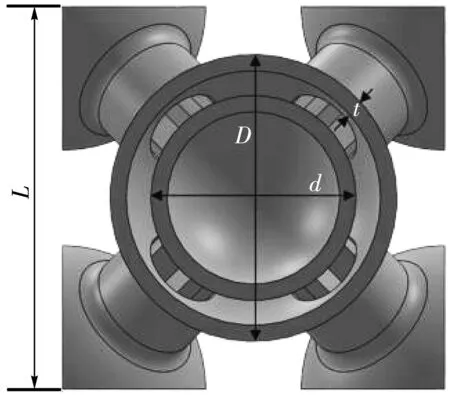
(b) 体心、简单混合结构剖面图图2 单胞结构剖面图Fig.2 Section of cell structure
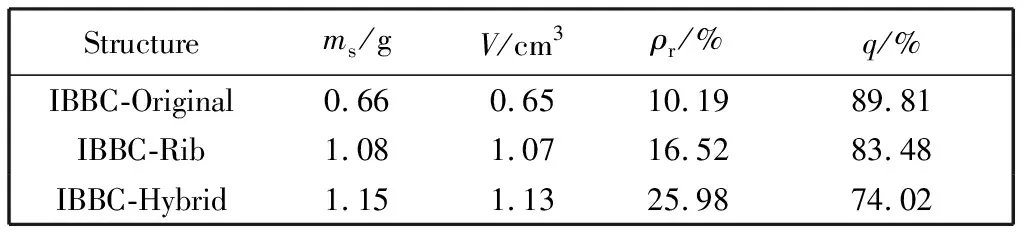
表1 三种结构的参数Tab.1 The parameters of three structural
以单胞结构为例,在密度ρ=1.01 g/cm3,壁厚t=0.5 mm,D=14 mm,d=10 mm时,三种结构的质量ms,体积V,相对密度ρr和孔隙率q分别如表1 所示.
1.2 有限元模型
在进行有限元仿真前先通过准静态拉伸试验来测试尼龙HP PA12材料的力学性能,3D打印时沿拉伸方向纵向成型,与多胞结构成型方向一致,典型拉伸试验结果如图3 所示. 由图3 可知,材料屈服强度约30 MPa,抗拉极限约36 MPa,断裂延伸率约11%. 压缩实验使用万能试验机进行,将试样垂直放置,并在上方放置垫块,使其只能受到轴向载荷作用,实验中以2 mm/min的速度进行压缩.
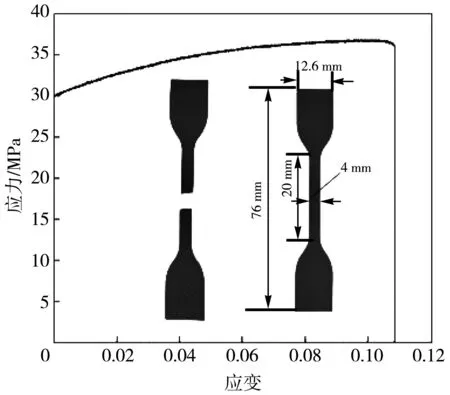
图3 材料应力应变曲线Fig.3 Stress-strain curve of material
采用SOLIDWORKS建立具有不同结构的三维仿体心立方多孔材料模型单胞结构,然后通过HYPERMESH剖分网格,将划分好的网格进行阵列处理,再将阵列完成的网格进行粘接,防止其在计算过程中发生脱落,最后基于ANSYS/ LS-DYNA求解. 结构整体有限元模型如图3 所示,球壳类多胞薄壁结构有限元模型均采用Shell 163单元划分,上下压头材料选用线弹性材料模型描述,材质为钢. 采用*MAT_PIECEWISE_LINEAR_PLASTICITY材料模型描述点阵结构,密度ρ=1.01 g/cm3,弹性模量E=1.8 GPa,泊松比为0.42. 在底座上施加三个方向的固定约束,压头施加位移-时间曲线来实现不同速度的恒速压缩. 球壳类多胞薄壁结构与压头、底座之间分别设置自动点面接触来描述其相互作用,考虑到薄壁结构压缩过程中产生的折叠,薄壁结构设置自动单面接触. 在本文中,为了提高计算效率,全部采用壳单元进行网格的划分与有限元仿真计算.
1.3 主要指标
针对薄壁结构,可采用以下指标评估其抗冲击和能量吸收性能:
1) 总吸能(Energy Absorption,EA)
总吸能是薄壁管在压溃过程中所吸收的总能量,是薄壁管的吸能特性的直观体现,其表达式为

(3)
式中:δ为当前压缩位移;x为积分变量.
2) 比吸能(Specific Energy Absorption,SEA)
比吸能是单位质量的薄壁管吸收的能量,用来评估能量吸收的效率,其表达式为
ESA=EA/mb,
(4)
式中:mb为薄壁管的总质量.
3) 平均压溃力(Mean Crush Force, MCF)
平均压溃力是衡量薄壁管缓冲吸能大小的一个重要指标,MCF的曲线越趋近于水平,水平平台段的值越大,说明该薄壁管的缓冲吸能效率越高,其表达式为
FMC=EA/δ.
(5)
2 实验与数值模拟结果
2.1 数值模拟和实验结果
实验选用I-H结构进行准静态压缩试验,其数值模拟和实验结果如图4 所示.
由图4 可知,实验所得压溃载荷值比数值模拟结果的低,主要是由于3D打印试样存在初始结构缺陷,分层成型中层间结合强度较低,因此,薄壁结构在拉伸时容易沿层间出现断裂,尤其是倾斜的连接管与球壳结合位置容易产生拉伸破坏,从而降低结构刚度和承载能力,未能真正反映结构的压溃吸能特性. 然而,从实验结果可知,结构压溃载荷位移曲线较为平整,说明该结构可提供稳定有序的反馈载荷,适用于抗冲击结构设计. 由图4(b) 可知,该结构在受到轴向载荷时会逐层开始压缩,在位移量较小时会发生弹性变形,使载荷位移曲线快速上升,当载荷达到一定值的时候第一层的连接管首先发生坍塌变形,然后外球结构也跟随其发生大变形,这个阶段载荷会逐渐降低,随着位移量的增大,发生坍塌的第一层结构会产生自接触,这时其载荷位移曲线会有所上升,直至下一层结构发生坍塌变形. 在最后一层结构发生坍塌变形后,整个结构中的空隙会随着位移量的持续增加而减少,进入了致密化阶段. 数值模拟中并未考虑材料和结构缺陷,因此所得到的载荷水平较高. 随着压缩量的增大,倾斜连接管和肋板失效后,结构进入球壳薄壁的压溃阶段,此时实验和数值模拟结果相差较小. 通过实验和仿真结果的对比可以看出,通过3D打印制备的三维球壳类多胞薄壁结构的压溃力学行为受初始结构缺陷的影响较大,因此,本文主要采用数值模拟方法研究构型因素对结构性能的影响.
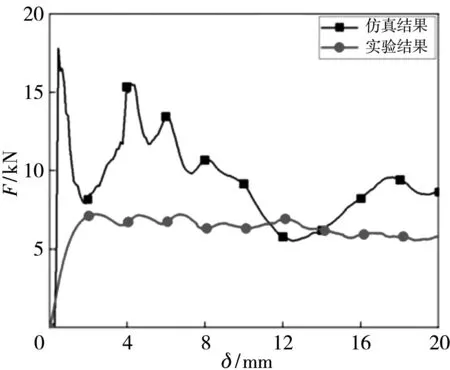

(a) 载荷曲线(b) 变形模式对比结果图4 实验和数值模拟结果Fig.4 Experimental and numerical simulation results
2.2 壁厚对结构吸能特性的影响
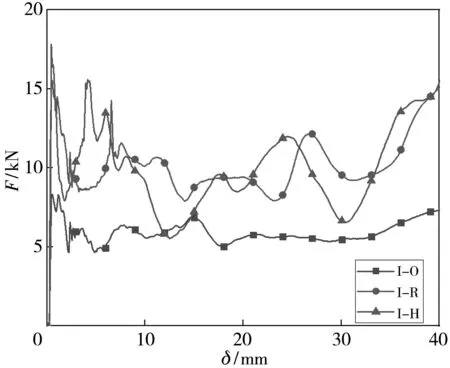
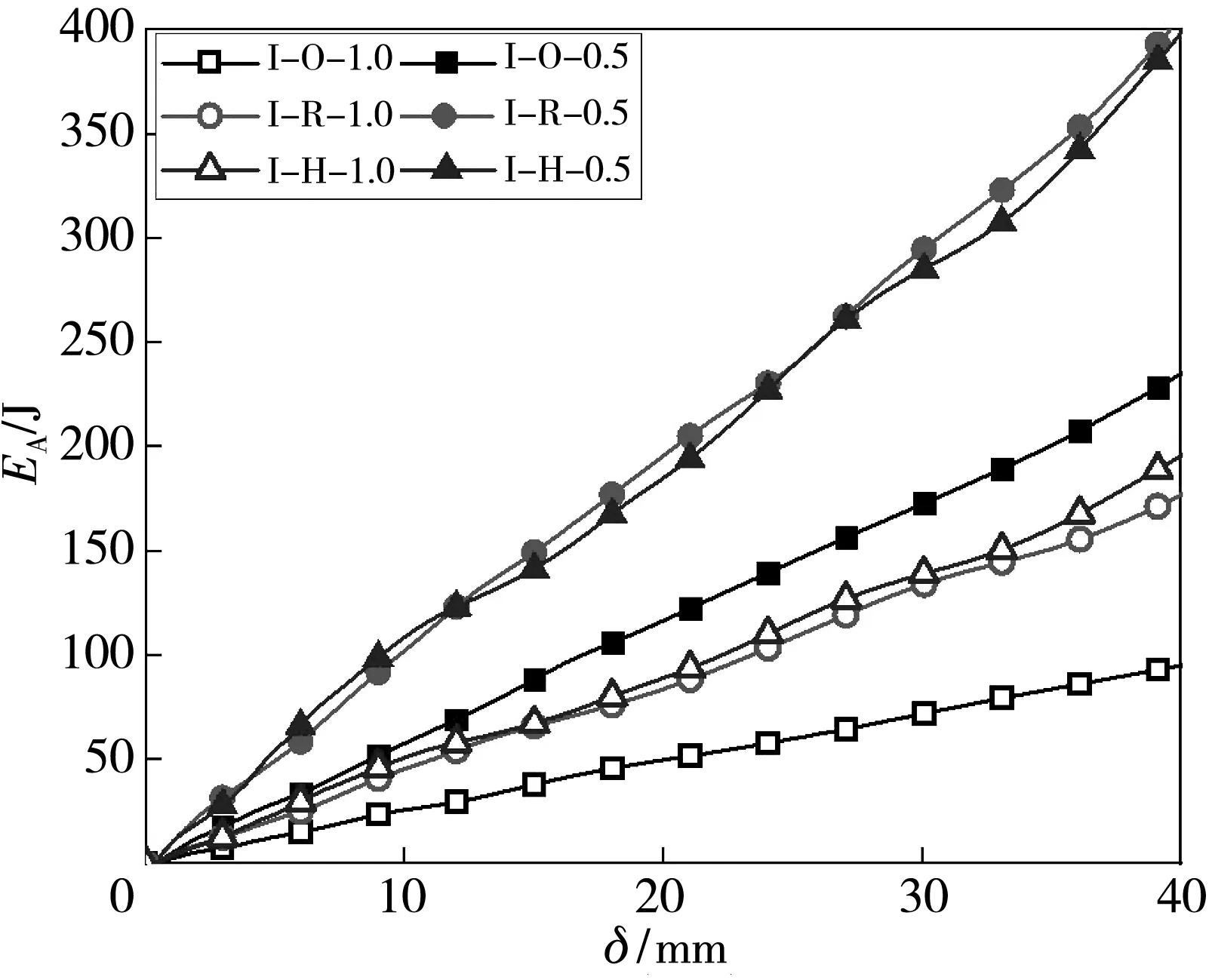
考虑到3D打印试样初始缺陷导致的实验结果的离散性,本文采用数值模拟方式来研究不同壁厚对三种结构的吸能特性的影响,为了方便计算,设置模型外球直径D为14 mm,内球直径d为10mm,连接管与水平面的夹角θ为45°,连接管长度h为3 mm,点阵结构总长度L为55.92 mm. 图5(a)、图5(b)和表2 为壁厚t分别取 0.5 mm和1.0 mm时,三种结构的轴向压溃数值模拟结果.
(a) t=0.5 mm
(b) t=1.0 mm

(c) 两种壁厚的MCF对比
(d) 两种壁厚的SEA对比图5 三种结构的压溃载荷曲线Fig.5 Crushing load curves of three structures
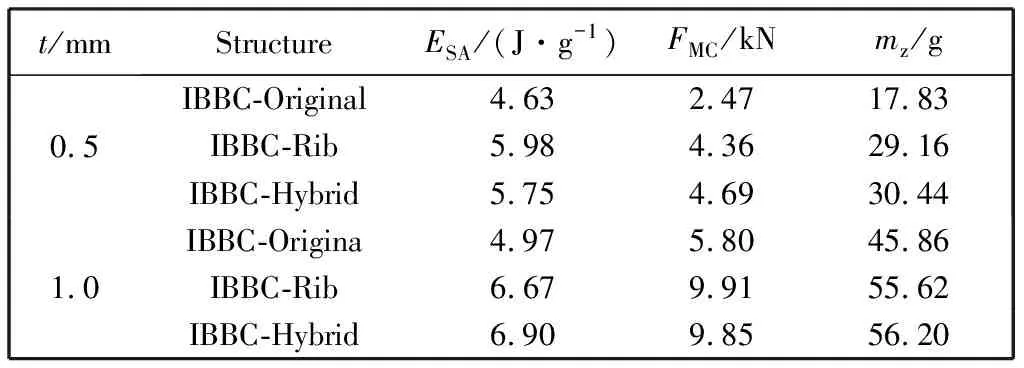
表2 壁厚对三种结构吸能特性的影响Tab.2 Effect of wall thickness on energy absorption characteristics of three structures
由图5 可知,壁厚为0.5 mm时,两种增强结构的压溃载荷曲线基本一致,均比IBBC结构提高了96%~106%,提升非常显著. 三种结构的平均压溃力和比吸能等指标如表2 所示,比吸能取39.14 mm处. 两种增强结构的SEA均高于I-O结构,I-R和I-H相较于I-O结构分别提高约29.16%和24.19%,两种增强结构的SEA相差不大,仅有4%的差距. 两种增强结构的MCF相较于I-O结构提升很大,分别提升了76.52%和 89.88%,两种增强结构的MCF相差也很小,仅有7.56%. 在壁厚为1.0 mm时,三种IBBC结构所得的曲线与0. 5 mm 时较为一致,I-R和I-H结构的SEA和MCF相差较小,分别只有3.45%和0.61%,但和I-O结构相比分别增长了34.21%和38.83%, 70.86% 和69.83%. 以上结果说明两种增强结构可以显著提高结构的吸能特性,并且改变壁厚可以使两种增强结构更加稳定,使SEA和MCF进一步提高.
2.3 角度及外层球壳对IBBC-R吸能特性的影响
上文模拟结果表明两种增强结构的吸能特性相较于原始的IBBC结构都有较为明显的提高,但两种结构中I-R结构的质量相较于I-H结构而言较小,下面将选用I-R结构来进一步研究IBBC结构的吸能特性. 考虑到仿真实验中连接管和外球结构会率先产生破坏坍塌,分别讨论以下两种情况的吸能特性:1) 改变连接管与水平面之间的角度θ,使其在压缩过程中可以产生折叠从而提高吸能特性的情况;2) 去掉外球结构对吸能特性影响的情况. 根据以上情况设计了如图6所示的三种I-R改进结构,其材料参数如表3 所示.
图7 为四种结构轴向压溃载荷和吸能指标的数值模拟结果,因为当连接管角度与水平面成60°时,其高度会发生变化,这时L为74.52 mm,在选取SEA值时应考虑该问题,选取70%压缩量处即39.14 mm与52.16 mm处进行对比. 如图7 所示,压缩开始时会出现峰值现象,峰值出现说明该结构在承受轴向载荷而进行压溃时,连接管和外球处会首先进行折叠,并产生失稳,发生预折叠. 同时,由图7 和表4 对比可知:连接管与水平面所成角度越大,结构吸能特性越差;当连接管与水平面成45°时,I-R-HO-45和I-R-NO-45的MCF分别比I-R-HO-60和I-R-NO-60结构高47.30% 和79.57%,SEA分别提升了10.54%和26.33%. 由此可以得出,当有外球时,这两种结构的差距会比没有外球时更小,说明外球会加强结构的承载能力;而且通过其应力云图可以清楚地看出,在相同压缩量处,有外球的结构时其连接管的变形会被外球所限制,而不会像无外球时那样直接坍塌,同时,在压缩过程中无外球时,其应力主要集中在内球上,使内球更容易发生应力集中而发生破坏坍塌,而有外球时其应力主要集中在外球上,内球并未有明显的应力集中现象,这就可以使内球充分地进行压缩,从而获得更佳的吸能特性.
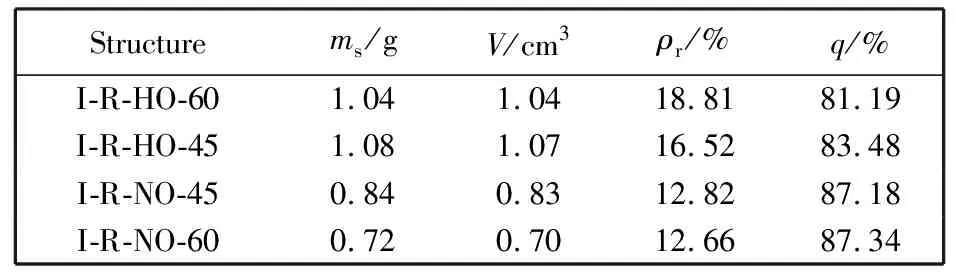
表3 四种改进结构的参数Tab.3 Four improved structural parameters

表4 不同结构吸能指标Tab.4 Energy absorption index of different structures
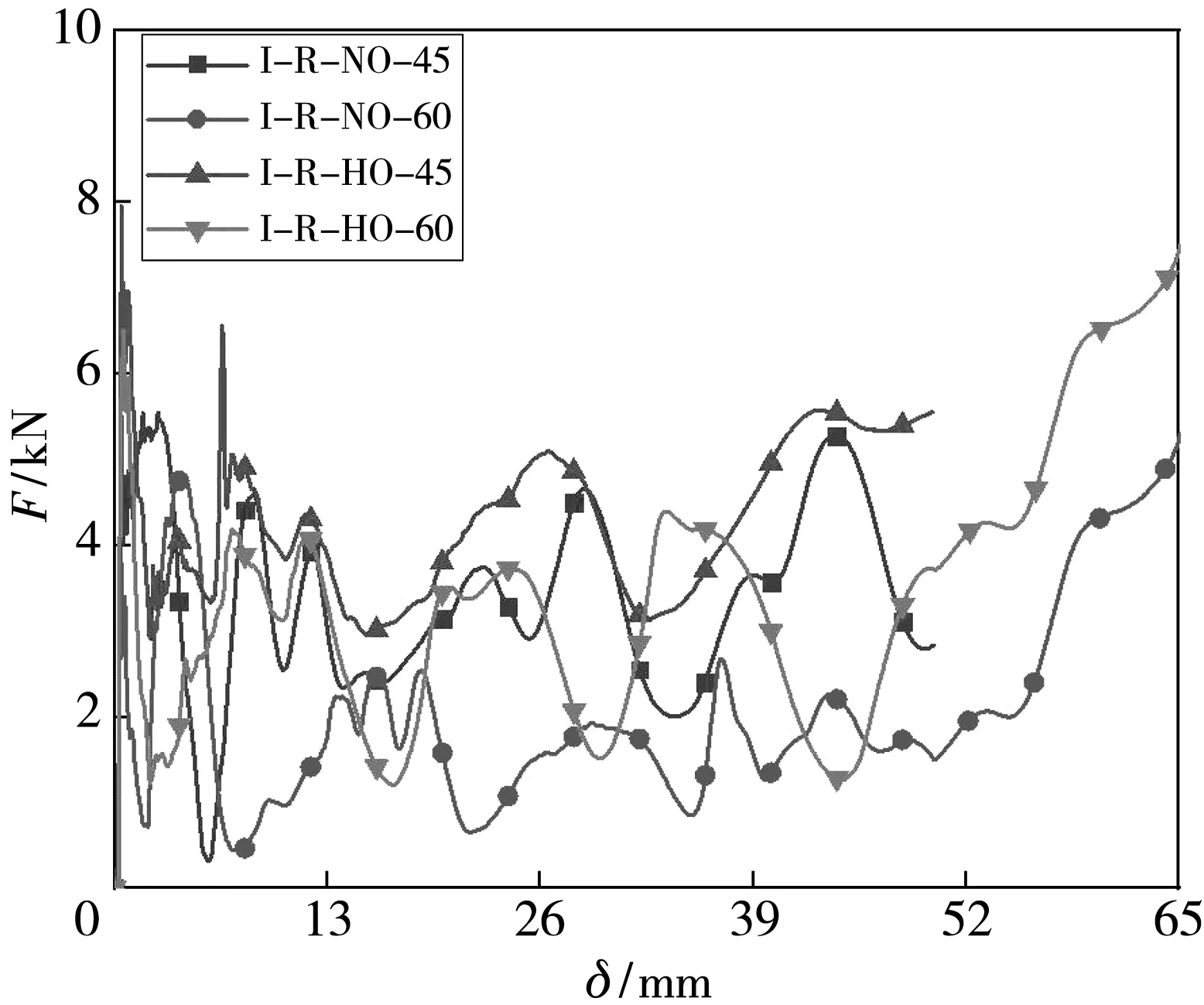
(a) 压溃载荷仿真结果对比
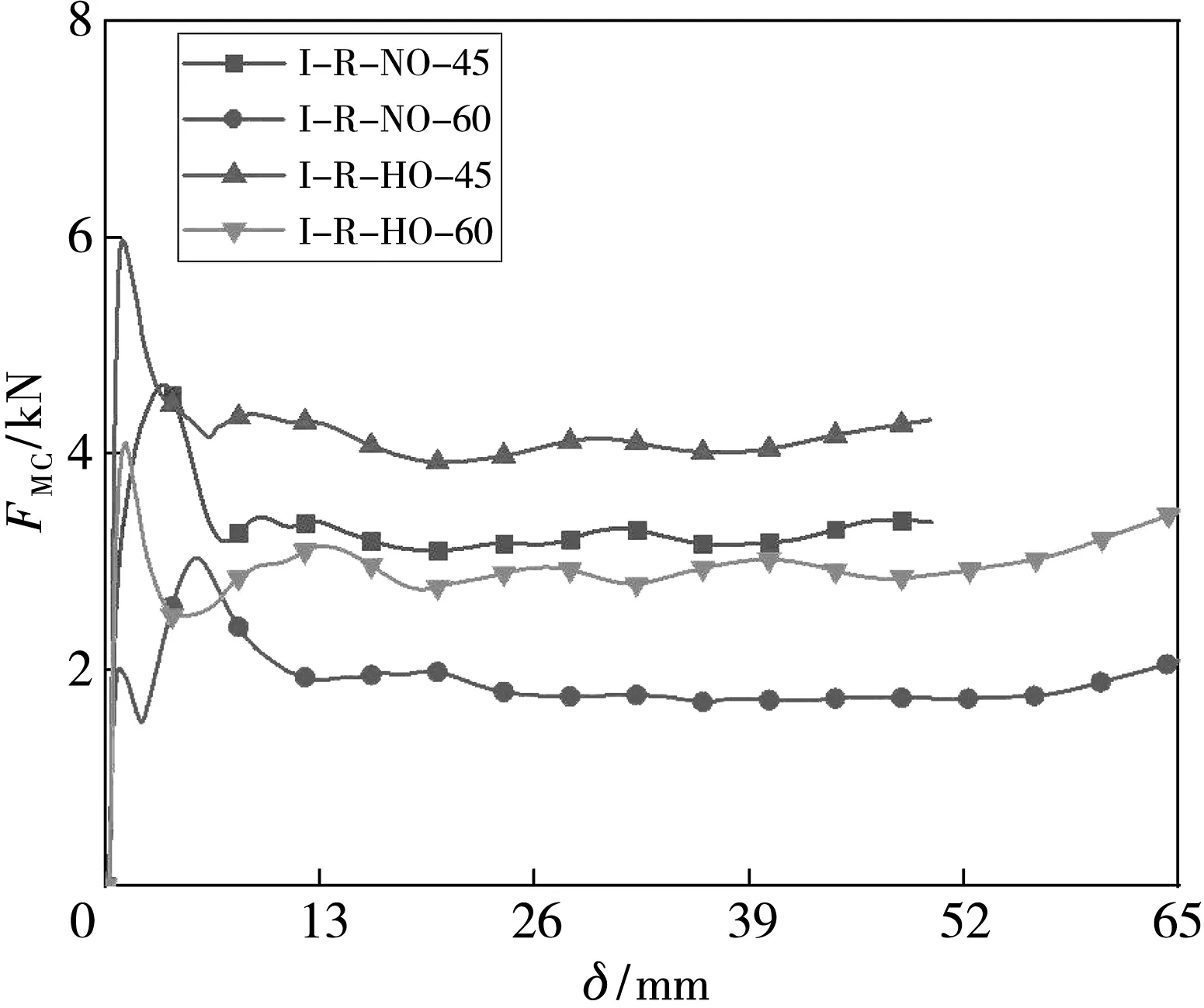
(b) MCF仿真结果对比
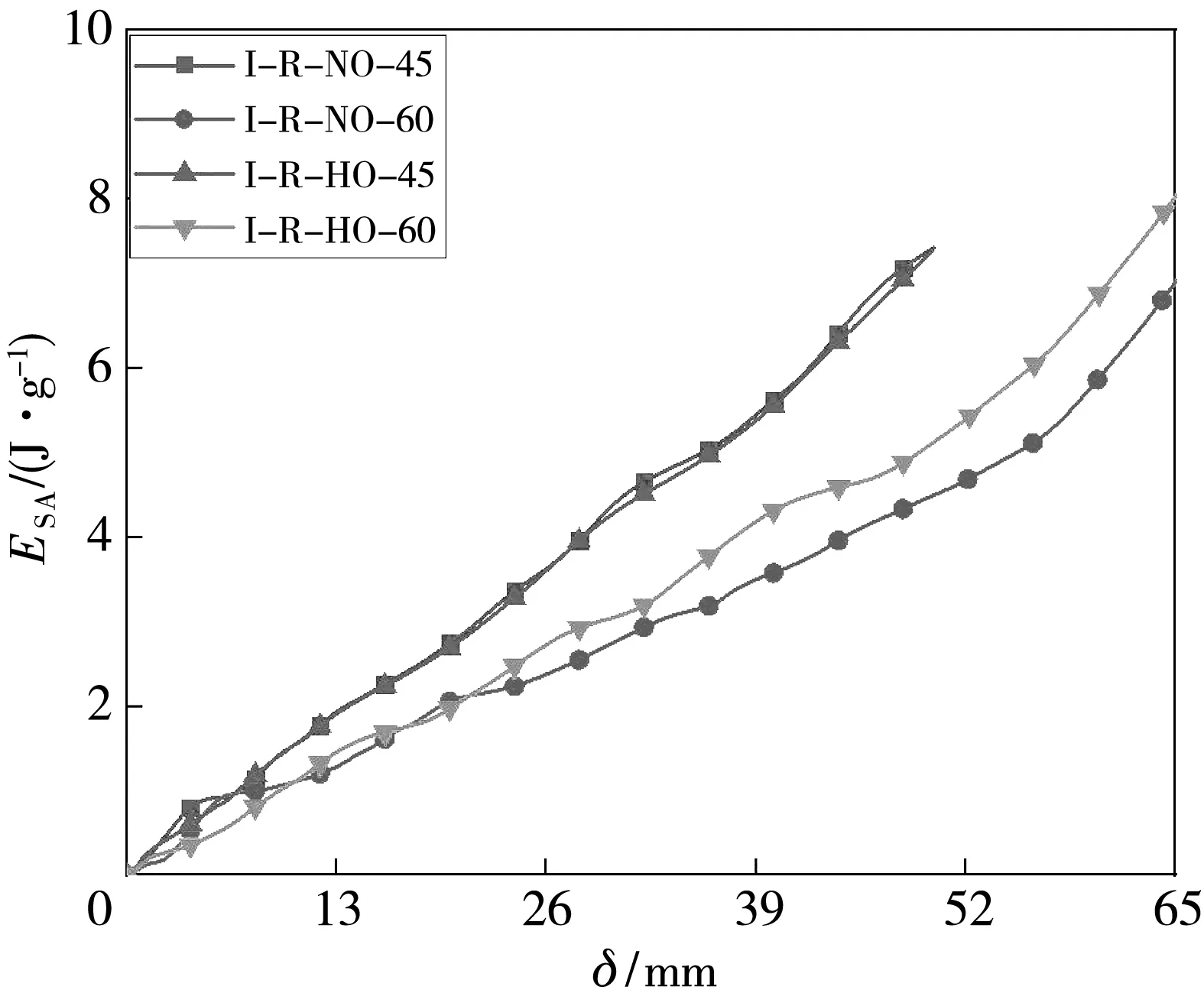
(c) SEA仿真结果对比
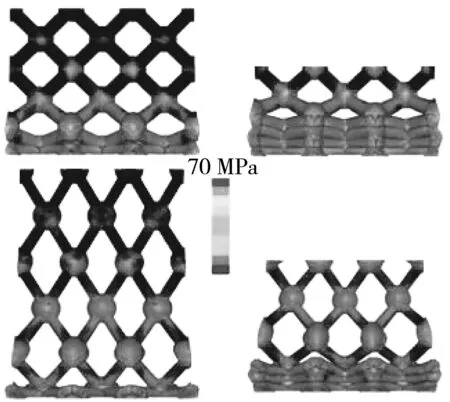
(d) NO结构变形模式

(e) HO结构变形模式
3 能量吸收特性
3.1 连接管角度对单胞结构的影响
由上文可知连接管角度的不同会对结构的吸能特性产生影响,为了更清晰地获得这些能量吸收的变化规律,在分析时采用放大4倍的单胞结构的有限元模型,如图8 所示.

图8 单胞结构有限元模型Fig.8 Finite element model of single cell structure
同时,为方便研究该结构受到轴向载荷时其内部的能量吸收规律,故将该结构的单胞结构划分成连接肋(CR)、连接管(CT)、内球(IB)和外球(OB)四部分. 对相同冲击速度下不同压缩位置的能量吸收进行对比,结果如图9 所示.

(a) 15 mm处能量吸收对比
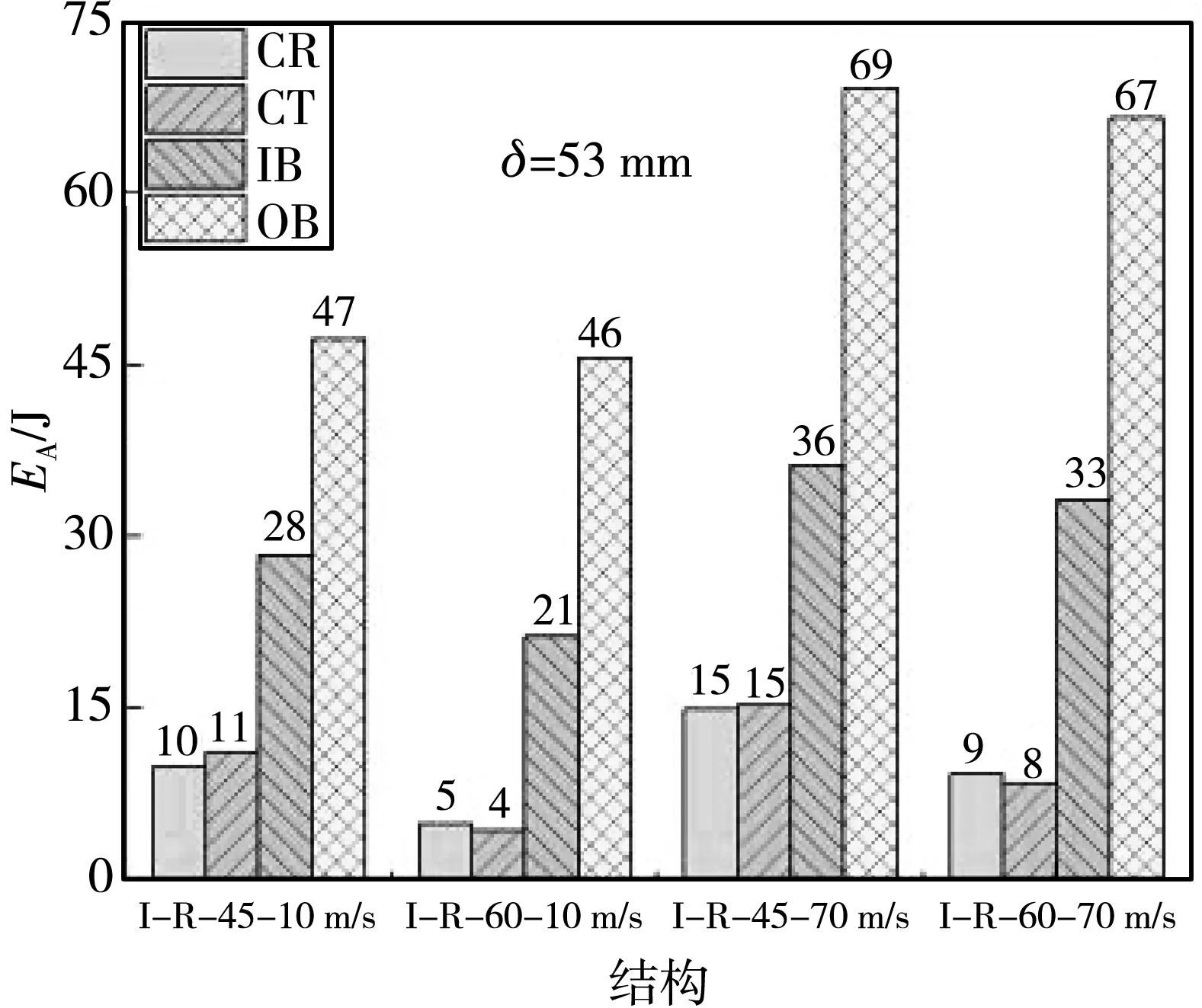
(b) 53 mm处能量吸收对比图9 CT角度对结构能量吸收的影响Fig.9 Influence of CT angle on structural energy absorption
由图9(a)可知:在压缩过程的初期,压缩速度为10 m/s时,图6中的四种结构中CT对其角度的变化最为敏感,其中,45°结构比60°结构的能量吸收率提高了187.5%,提升非常大,其次是OB对CT角度的变化有一定的敏感性,其能量吸收率提高了14.55%,CR和IB对CT角度的变化并不敏感,其能量吸收率并未有明显的提升或下降;当速度为70 m/s时,同样是CT对其角度的变化最为敏感,其能量吸收率提高了 192.86%;当速度由10 m/s提高到70 m/s时,CR对CT角度的变化也随之增长,其能量吸收率提高了26.09%,OB的能量吸收率提高了7.91%,相对于10 m/s速度而言有所降低.
由图9(b) 可知,在压缩过程的后期,当速度为10 m/s时,I-R-45比I-R-60的CR的能量吸收率提高了50%,CT的能量吸收率提高了175%,IB的能量吸收率33.33%,OB对CT角度的变化并不敏感,并未有明显的提升. 当速度为70 m/s时,I-R-45比I-R-60的CR的能量吸收率提高了66.67%,CT的能量吸收率提高了 87.5%,IB的能量吸收率提高了9.09%,OB对CT角度的变化并不敏感,并未有明显的提升.
综上对比可知,CT在不同速度和不同压缩量处对其角度的变化最为敏感,角度为45°时的能量吸收率比角度为60°时提升的多,在低速低位移量的情况下,CR、IB和OB对角度的变化并不敏感,但随着速度的增加,CR、IB和OB的能量吸收率也会随之增加,而在高位移量的情况下,OB的能量吸收率不会随着速度的增加而增加. CT角度不同时的CT折叠模式如图10 所示.
由图10 可以看出,在相同压缩量及70%处,I-R-45会有明显的压缩趋势,并且应力主要集中在CT上,使其可以进行一定的能量吸收,而I-R-60在压缩量为70%处并未有明显的压缩痕迹,在压缩量为80%处时才会有明显的压缩趋势. 以上分析说明,增加CT的角度会改变其能量的吸收模式,并延缓其致密化阶段的发生.
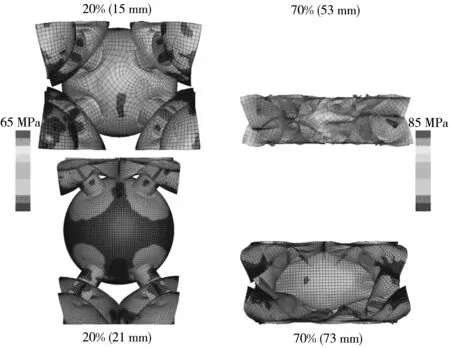
(a) 整体结构应力云图
(b) CT结构应力云图图10 I-R压缩70%的应力云图Fig.10 Stress nephogram for I-R compression of 70%
3.2 冲击速度对单胞结构的影响
冲击速度对薄壁结构的吸能特性和变形特征有显著的影响[12],故对效果较好的I-R-HO-45结构进行不同速度(10 m/s,40 m/s,70 m/s)冲击加载的数值模拟,其有限元模型如图8(a) 所示.
图11 为I-R-HO-45结构在不同速度下的压溃载荷和能量吸收曲线.
由图11 可知,随着冲击速度的增加,该结构的压溃载荷和能量吸收也随之增加,冲击速度为70 m/s 时SEA相较于其他两组速度分别增加了 48.17% 和86.18,MCF分别增加了85%和272%. 图11(d)为10 m/s和70 m/s 加载速度下该结构的应力云图,由图可知,当速度越大时,其压缩过程为更明显的渐进压缩,速度较小时其压缩过程为两侧向中间内、外球挤压,该折叠方式不利于提高结构的能量吸收效率. 由图11 的载荷位移曲线可知:在弹性变形阶段其弹性段刚度相差较大,说明弹性段刚度对应变率效应较为敏感;随着冲击速度的增加,其对应的峰值载荷有所增加,且大于承受准静态轴向载荷作用的试件,说明试件的强度对应变率效应也较为敏感;冲击速度为 40 m/s 与70 m/s时的载荷位移曲线具有相似的形状和趋势,区别仅为数值大小不同,表明冲击速度的增加并不会对结构的失效模式产生较大的影响.
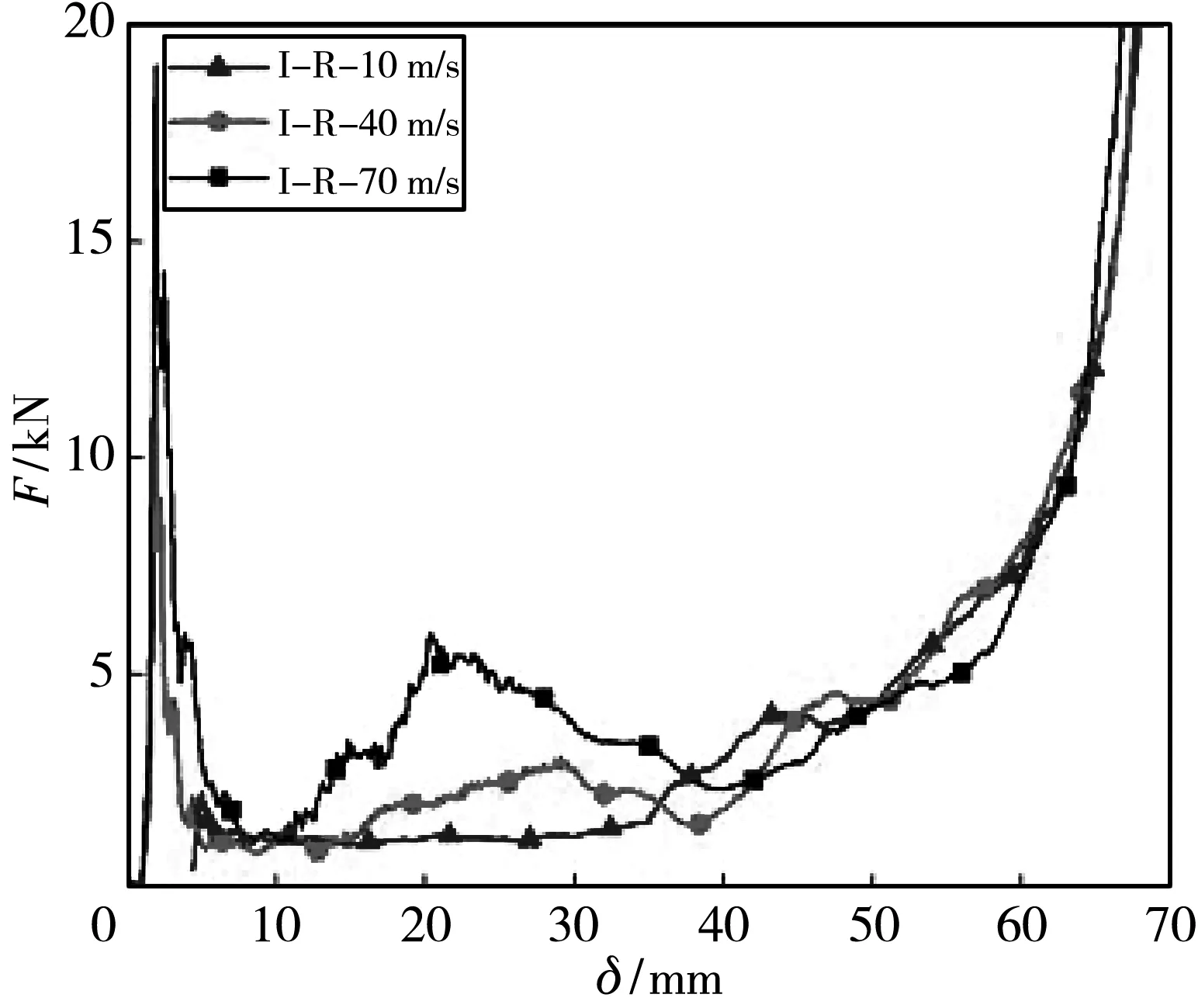
(a) 载荷仿真结果对比

(b) MCF仿真结果对比

(c) SEA仿真结果对比
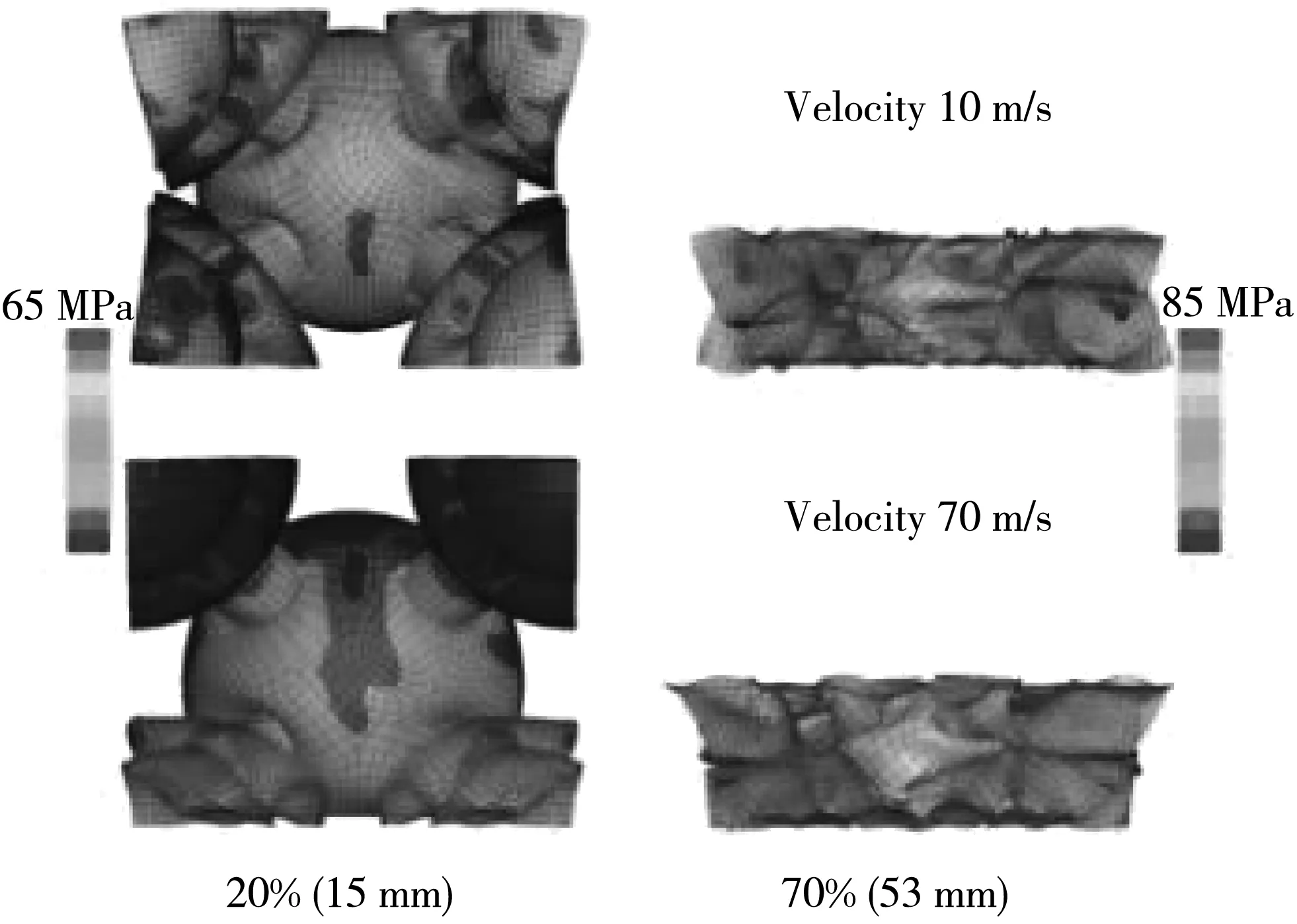
(d) 变形模式分析图11 单胞结构数值模拟结果Fig.11 Numerical simulation results of cell structure
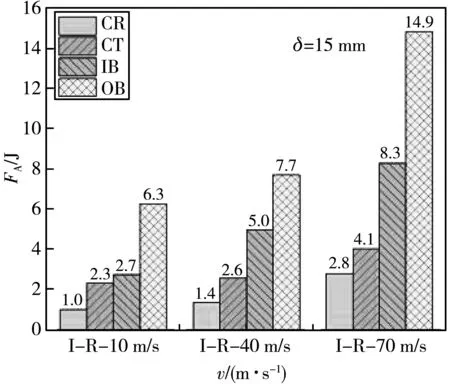
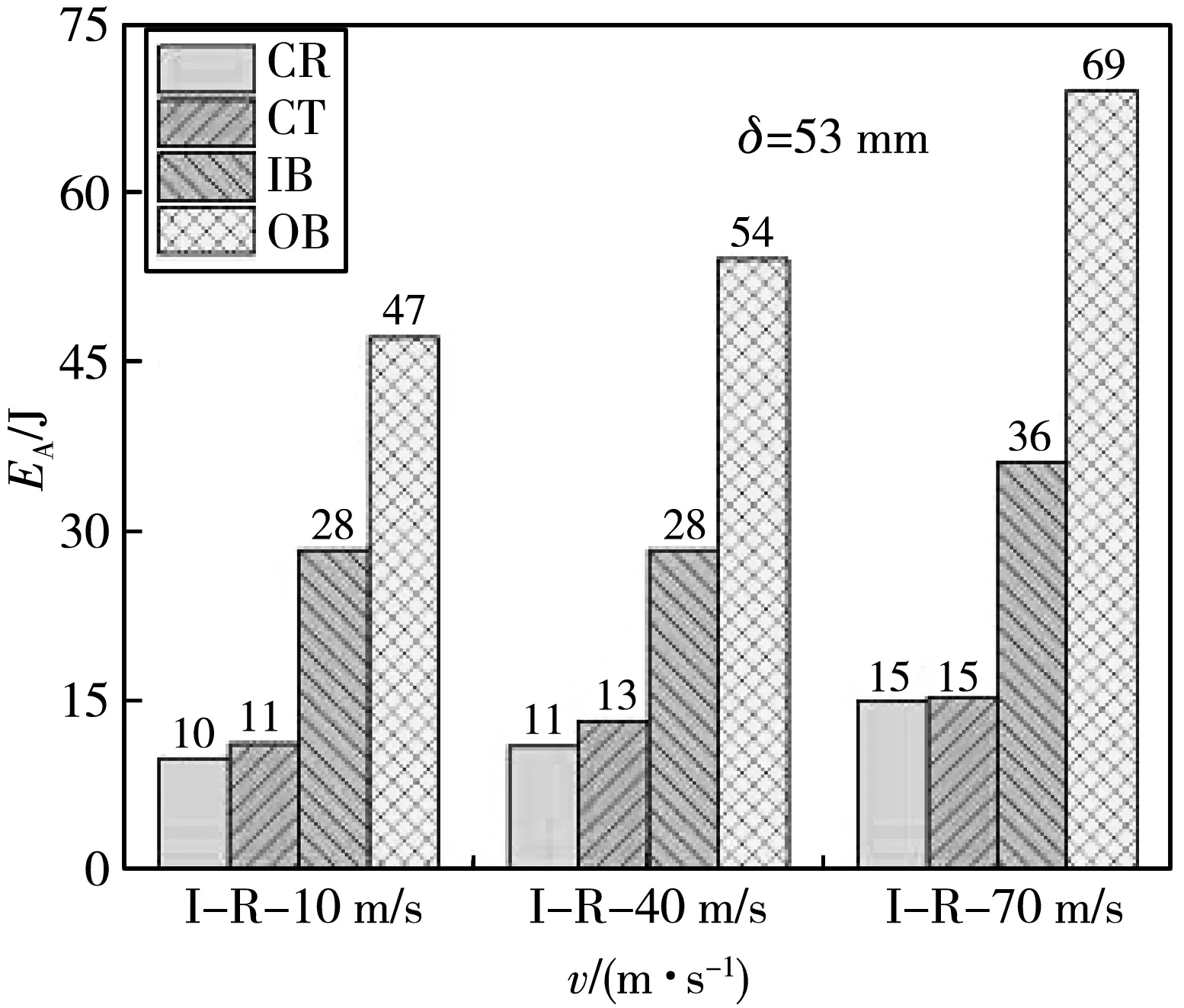
图12 为不同冲击速度下不同压缩位置的能量吸收对比结果.
(a) 15 mm处能量吸收对比
(b) 53 mm处能量吸收对比图12 冲击速度对结构能量吸收的影响Fig.12 Influence of impact velocity on energy absorption of structure
由图12(a)可知:在压缩初期,CR、CT、IB和OB对速度的敏感性都很强,CR的能量吸收率相对于前一种速度分别提高了40%和50%,CT的能量吸收率相对于前一种速度分别提高了13.04% 和57.69%,IB的能量吸收率相对于前一种速度分别提高了85.19%和66%,OB的能量吸收率相对于前一种速度分别提高了22.22%和 93.51%. IB对速度的变化最为敏感,在弹性变形阶段和大变形阶段前期其能量吸收率最佳;CR、CT和OB的能量吸收率也随着速度的增加而大幅度增加,其中,CT对速度的变化最不敏感,分析原因主要是由于CT所在位置使其不能进行充分的压缩,所以,速度对其影响没有那么明显.
在压缩过程的后期,CR的能量吸收率相对于前一种速度分别提高了10%和36%,CT的能量吸收率相对于前一种速度分别提高了18.18%和15.38%;IB的能量吸收率相对于前一种速度分别提高了0%和42.86%,OB的能量吸收率相对于前一种速度分别提高了 14.89% 和27.78%. 可以看出,CR、CT、IB和OB对速度的敏感性都在大幅下降,其中,速度为10 m/s与40 m/s时,CR和IB在该位移处有部分内部结构已经完成了大变形阶段,但并未进入致密化阶段;在速度为70 m/s时,CR和IB结构已经完成了大变形阶段而进入了致密化阶段,故其内能也随之增长,而CT和OB在这三种速度下并未进入致密化阶段,还会受到速度的影响.
考虑到该结构在压缩过程中有明显的渐进压缩特征,故对其惯性效应进行分析. 研究表明,蜂窝泡沫类材料在高速冲击下的惯性效应引起的载荷增量可表示为
Fin=ρmAmv2/εD,
(6)
式中:ρm为结构基体密度;Am为多胞管材料的横截面积;εD为结构最大压缩应变,本文取0.7. 计算可得三种速度下的惯性效应引起的载荷增量分别约为0.012 kN, 0.194 kN和0.594 kN. 由图11 中MCF的变化趋势可以看出,除了该结构在压缩过程中的轴向惯性效应外,结构压溃模式的改变是增强其吸能能力的主要原因.
4 结 论
本文基于体心立方结构进行了多胞壁结构增强设计,基于实验和数值模拟研究了模型形态、模型壁厚、连接管角度和冲击速度对其能量吸收和变形模式的影响,主要结论如下:
1) 对体心立方结构进行改造,发现在球体中心添加连接肋的结构(IBBC-Rib)和体心立方与简单立方相结合的结构(IBBC-Hybrid),其SEA和MCF相较于普通结构(IBBC-Simple)分别增长了24%~38%和71%~90%,MCF提升较为明显,说明增加内核和连接管可以改变结构在压缩时的折叠模式,能够增强其比吸能和承载能力.
2) I-R结构的吸能能力会随着连接管与水平面所成角度的增大而降低,并且外部球壳结构会阻碍连接管的破坏坍塌,能够增强其压缩吸能性能.
3) 连接管角度的变化会引起其吸能特性的改变,当压缩量相同时,角度小的结构拥有更优的能量吸收率,但连接管角度的增大会延长其大变形阶段. 在冲击速度为10 m/s~70 m/s时,连接管对速度的变化最不敏感,而连接肋、内球和外球的吸能特性会随着冲击速度的增加而增加.

