两类对称箭状矩阵的广义逆特征值问题

崔 萌，雷英杰

(中北大学 数学学院，山西 太原 030051)

0 引 言

矩阵的逆特征值问题[1-2]在许多学科和领域都有重要的应用，如自动控制、系统参数辨析、结构设计等[3]，如在振动力学中，离散系统的频率对应矩阵的特征值，模态对应于特征向量，此时，在给定频率和模态的情况下，如何找到原振动系统的问题就转化为矩阵逆特征值问题的求解. 在过去几十年里，此问题吸引了许多学者的研究，取得了显著的成果[4-15]，如Pickmann-Soto H等[4]研究了一类非对称的爪型矩阵和三对角矩阵的逆特征值问题；2020年，Zarch M B等[5]研究了一类具有两个特征对的无环矩阵的逆特征值问题；2021年，Fathi F等[7]利用奇异值变换的方法巧妙地构造了一个非对称箭型矩阵；Sharma D等[8]研究了对应图为路径和图为扫帚的矩阵的逆特征值问题等等. 参考上述学者的研究方法及矩阵的结构形式，将路图与扫帚图进行推广得到本文所研究的两类具有不同结构的广义矩阵. 本文通过两组特征对的方法研究了上述两类广义矩阵的逆构造的问题，得到了矩阵逆构造的具体条件，并以具体低阶数值实例验证了结果的准确性.

1 问 题

基于已有结果，针对路径图和扫帚图推广出本文所研究的两类矩阵对应的图，如图1 所示.

(a) T矩阵(b) A矩阵图1 矩阵对应的图Fig.1 Graph of matrices

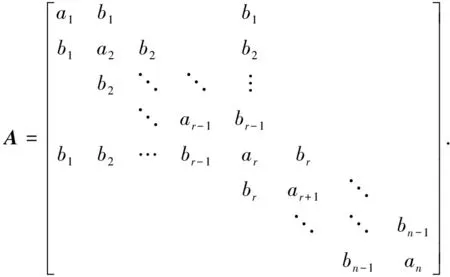
(2)

矩阵T与A均为广义对称箭状矩阵，其中bi,i=1,…,n-1均不为0.

问题Ⅰ：给定两个不同的实数λ,μ及X=(x1,x2,…,xn)T，Y=(y1,y2,…,yn)T两组非零向量，求构造形如矩阵T的充要条件，使得TX=λX,TY=μY.

问题Ⅱ：给定条件同问题Ⅰ，求构造形如矩阵A的充要条件，使得AX=λX,AY=μY.

2 预备知识

约定

(3)

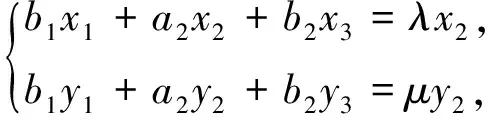
(4)

i=3,…,r,

(5)

i=r+1,…,n-1,

(6)

(7)

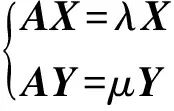
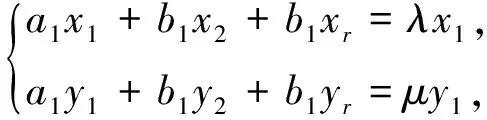
(8)

i=2,…,r-2,

(9)

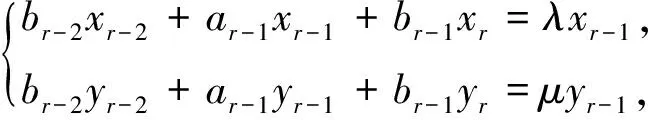
(10)

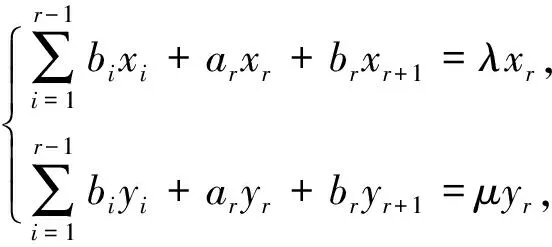
(11)

i=r+1,…,n-1,

(12)

(13)

3 问题的解

定理 1问题Ⅰ有唯一解等价于以下条件成立：

1)Di-1≠0,i=2,…,n；

2)Mi+Di-1≠0,i=3,…,r；

证明 充分性由条件(1)可知xi与yi(i=1,…,n)不会同时为0.

当i=n时，根据式(7)得bn-1(xnyn-1-xn-1yn)=(μ-λ)xnyn，再由条件(1)计算可得

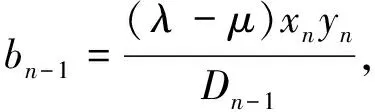
(14)

由条件(1)可知xn与yn不同时为0，根据计算分别可得

(15)

以下证明均类似.

当i=r+1,…,n-1时，同理根据式(6)及条件(1)求解出

(16)

已知xi与yi(i=r+1,…,n-1)不同时为0，可分别计算出

(17)

当i=3,…,r时，根据式(6)及条件(1)和(2)求解得

(18)

已知xi与yi(i=3,…,r)不同时为0，可分别计算出

(19)

当i=2时，根据式(4)和条件(1)求解得

(20)

已知x2与y2不同时为0，可分别计算出

(21)

当i=1时，根据式(3)、条件(1)及上述计算所得bi(i=1,…,r-1)求解得

(22)

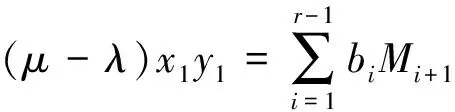
定理 2问题Ⅱ有唯一解等价于以下条件成立：

1)Di≠0,i=1,…,n-1，Er-1≠0；

2)Di+Ei≠0,i=1,…,r-2；

证明 充分性由条件(1)可知xi与yi(i=1,…,n)不同时为0.

当i=1时，根据式(8)可以推出b1(D1+E1)=(μ-λ)x1y1，再由条件(2)计算可得

(23)

根据条件(1)知x1与y1不同时为0，可分别计算得

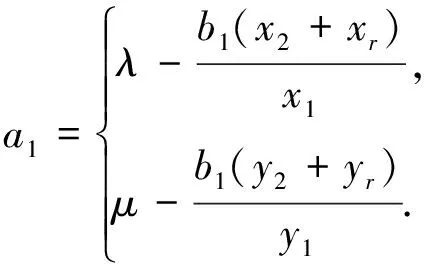
(24)

以下证明均类似.

当i=2,…,r-2时，根据式(9)及条件(1), (2)类似于上述计算可得bi与ai的唯一值为

(25)

(26)

当i=r-1时，根据式(10)及条件(1)类似计算可得

(27)

(28)

当i=r时，根据式(11)及条件(1)类似计算可得

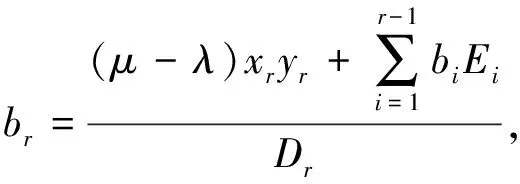
(29)

(30)

当i=r+1,…,n-1时，根据式(12)及条件(1)计算可得

(31)

(32)

当i=n时，根据式(13)及条件(1)计算可得

(33)

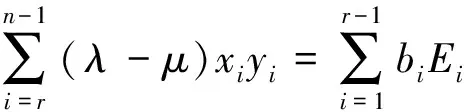
4 算法及实例

4.1 数值算法

问题Ⅰ的算法(算法1)

1.输入λ，μ，X，Y；

2.若λ，μ，X，Y满足定理1中的条件(1), (2), (3)则继续；否则算法结束.

3.当i=n时，由式(14)，式(15)分别计算bn-1和an；

4.当i=r+1,…,n-1时，由式(16)，式(17)分别计算bi-1和ai；

5.当i=3,…,r时，由式(18)，式(19)分别计算bi-1和ai；

6.当i=2时，由式(20)，式(21)分别计算b1和a2；

7.当i=1时，由式(22)计算a1；

8.输出：矩阵T，ai，bi-1.

问题Ⅱ的数值算法(算法2)

1.输入λ，μ，X，Y；

2.若λ，μ，X，Y满足定理2中的条件(1)，(2)，(3)则继续；否则算法结束.

3.当i=1时，由式(23)，式(24)分别计算b1和a1；

4.当i=2,…,r-2时，由式(25)，式(26)分别计算bi和ai；

5.当i=r-1时，由式(27)，式(28)分别计算br-1和ar-1；

6.当i=r时，由式(29)，式(30)分别计算br和ar；

7.当i=r+1,…,n-1时，由式(31)，式(32)分别计算bi和ai；

8.当i=n时，由式(33)计算an；

9.输出：矩阵A，ai，bi.

4.2 数值实例

例 1给定X=(-1，2，-0.5，-1，1，4)T,λ=3，μ=1，Y=(1，1，4，2，-1，1)T，求类似于形式(1)的矩阵T6.

解根据已知条件利用MATLAB R2016a计算得D1=-3，D2=8.5，D3=3，D4=-1，D5=5，M3=-3.5，M4=-1；满足定理1的条件(1)，(2)，(3)，通过算法1计算得

重新使用MATLAB R2016a计算所求得矩阵T6的特征值为-13.584 5，-1.459 8，0.648 8，1.000 0，2.828 9，3.000 0. 其中，1.000 0与3.000 0 分别为给定的λ与μ，其对应的特征多项式分别为X=(0.207 4,-0.414 8,0.103 7,0.207 4,-0.207 4,-0.829 6)T,Y=(0.204 1,0.204 1,0.816 5, 0.408 2,-0.204 1,0.204 1)T.易验证(λ,X)和(μ,Y)均为T6的特征对.

例 2给定X=(-1，2，1，0.25,-1,0.5)T,λ=1，μ=2，Y=(1，1,-1，2，1，1)T，求类似于形式(2)的矩阵A6.

解根据已知条件利用MATLAB R2016a计算得D1=-3，D2=-3，D3=2.25，D4=2.25，D5=-1.5，E1=-2.25，E2=3.75，E3=2.25；满足定理2的条件(1)，(2)，(3)，通过算法2计算得

重新使用MATLAB R2016a计算所求得矩阵A6的特征值为-5.705 7，1.000 0，1.011 8，1.392 4，1.809 5，2.000 0.其中, 1.000 0与2.000 0 分别为给定的λ与μ，其对应的特征多项式分别为X=(-0.369 8,0.739 6,0.369 8,0.092 5,-0.369 8,0.184 9)T,Y=(0.333 3,0.333 3,-0.333 3,0.666 7,0.333 3,0.333 3)T.易验证(λ,X)和(μ,Y)均为A6的特征对.