加载速率和加载位置对炸药缝隙扩展过程影响的数值模拟

楼建锋，张树道

（北京应用物理与计算数学研究所，北京 100094）

0 引言

高能炸药是由炸药颗粒、黏结剂等构成的非均质复合材料，力学性能受加工工艺和制备过程的影响，动力学响应行为还依赖于使用环境、结构约束和加载条件等因素［1-5］。炸药部件在制备成型和使用过程中都可能会产生裂纹，影响其力学性能和爆轰性能。外界刺激下炸药的动力学响应，特别是弱载荷作用下炸药的损伤断裂等行为，不仅影响炸药非冲击点火行为，也会影响点火后反应演化过程及其反应剧烈程度，是目前炸药安全性研究领域关注的重点之一。

为了研究弱载荷作用下炸药的损伤断裂行为，通常是开展准静态或动态力学性能实验，例如三点弯曲试验、霍普金森压杆实验、巴西试验等，在实验中获取材料的应力应变关系、动态破坏强度等特征量，并进一步构建材料本构模型来预测材料的动力学响应［6-12］。随着计算方法的发展，细观损伤模型及其数值模拟方法已成为炸药损伤研究的热点［13-16］，然而真实炸药材料的微细观建模比较困难，这些方法很难应用于复杂结构工程试验的模拟，实际工程问题的分析还得依赖于宏观唯像模型。

由于高能复合炸药与混凝土类材料在结构组成上存在一定的相似性，高能炸药主要由高能炸药颗粒和黏结剂等基体构成，而混凝土材料由骨料和砂浆组成，在常温常压下都是脆性材料，两者的破坏强度也比较接近（几十兆帕），因此，本研究尝试采用混凝土类材料的宏观本构模型［17］来描述高能炸药的动力学响应。

对于炸药材料，由于实验加载过程中存在反应放能的风险，能较好描述炸药损伤断裂演化规律的实验很难开展，系统分析加载条件、结构约束等因素对裂缝产生机制和扩展规律影响的工作很少。因此，本研究针对钝感炸药的裂缝起裂和扩展过程开展了数值模拟研究，着重分析了加载速率和加载位置对断裂模式及裂缝演化过程的影响规律。

1 数值模拟方法及算例验证

三点弯曲试验是材料弯曲断裂行为研究及其力学性能测试的重要试验，在金属材料的弯曲性能研究和岩石、混凝土等脆性材料的断裂力学性能研究中都有广泛应用，近年来该试验也逐渐被应用于含能材料的动力学响应分析［6-7］。三点弯曲试验中，给炸药试件施加载荷P，会发生局部应力集中现象，一旦超过材料破坏强度就会逐渐发生断裂破碎，结构示意图如图1所示。要准确描述这个过程，需要有合理的失效断裂模型和参数。为此，本研究使用有限元程序LS-DYNA 建模［18-19］，采用拉氏算法，在充分考虑网格收敛性后，选取网格单元尺寸为0.1mm。通过Riedel-Hiermaier-Thoma（RHT）本构模型和侵蚀算法来开展钝感炸药三点弯曲试验断裂现象的数值模拟，分析炸药起裂行为和裂缝演化过程及其影响因素；加载部件钢柱使用刚体本构模型（*MAT_RIGID）。

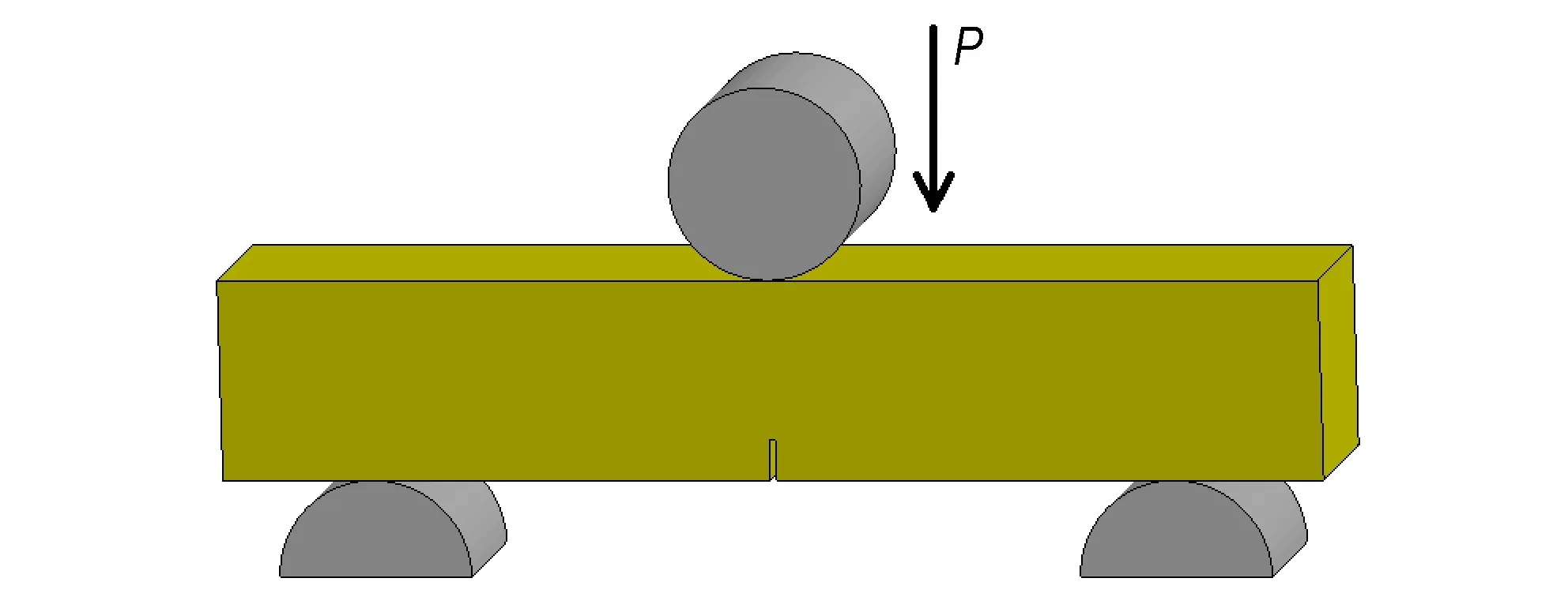
图1 三点弯曲试验装置结构示意图Fig.1 Configuration of three-point bending test

国内外对混凝土的材料本构模型开展了大量有效的 研 究 工 作 ，其 中 ，Riedel［17］通 过 改 进Holmquist-Johnson-Cook（HJC）模 型 提 出 了RHT 模型。该模型引入了偏应力张量第三不变量对破坏面的影响，引入三个强度极限面概念［17，19］，即弹性极限面、失效面和残余强度面，它们分别描述材料的初始屈服强度、失效强度及残余强度的变化规律，该模型能综合反映材料的拉压异性、应变率效应、应变硬化、软化与失效等现象，更全面地反映材料在不同应力状态下的动态力学行为。当材料强度达到失效面的极限强度时，损伤开始累积；对塑性应变进行积分获得材料损伤值。RHT 模型中包含了弹性、线性强化和损伤软化3 个阶段，30 余个参数。

RHT 模型中，失效面对应的失效函数Yfail表示为：

以上各式中，pspall是层裂强度，MPa；FC是抗压强度，MPa；J2和J3分别是偏应力张量第二和第三不变量；A、N、α、δ、Q0和B是材料系数，ε̇0= 3 × 10-6s-1。

弹性极限面的方程为：

式（9）中，Af和Nf分别是残余强度面的系数和指数。

失效面和残余强度面之间的状态也是通过插值得到，

式（11）中，D1和D2是材料损伤系数，εp为塑形应变。

本研究通过设置合理的拉伸破坏强度、压缩破坏强度和最大等效应变，构建了多种模式组合的失效判据，并利用侵蚀算法处理大变形网格单元，实现了材料失效断裂的仿真模拟。针对文献［6］中的三点弯曲试验开展了大量数值模拟，结合试验数据分析了计算模型的参数敏感性，进一步标定了主要的计算参数（见表1）。其中，压缩强度、拉伸强度和剪切模量参考了文献［8］的实验结果，屈服面和损伤相关的模型参数主要是通过数值模拟进行拟合，经过对比模型曲线中弹性段、线性强化段以及损伤软化段的变化规律，结合参数敏感性分析再不断优化。

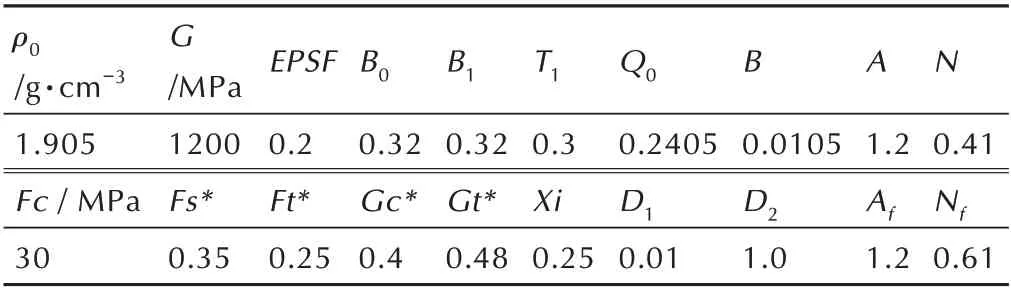
表1 LX-17 炸药的主要计算参数Table 1 Main parameters of LX-17

本研究对文献［6］中的三点弯曲试验进行了数值模拟，获得了炸药起裂和裂缝演化过程的特征图像。计算模型中样品的初始裂缝长度是2 mm，宽度是0.3 mm，加载速率是2.54×10-3mm·s-1。炸药样品中的应力变化云图和裂缝演化过程的特征图像如图2 所示，可以看到，在外载荷作用下，首先在裂缝尖形成较大的应力集中状态（图2a），随着外载荷的增加，应力集中区域不断地从裂缝尖附近向周围扩展，当裂缝尖的拉应力超过材料拉伸破坏强度时，就产生了新的裂缝（图2b），而随着应力继续在裂缝尖聚集，缝隙会进一步向加载位置扩展（图2c），最后使得样品断裂形成两段（图2d）。数值模拟得到了荷载随样品位移变化的曲线，跟试验测试曲线的对比情况如图3 所示，荷载峰值和变化趋势都互相符合较好。

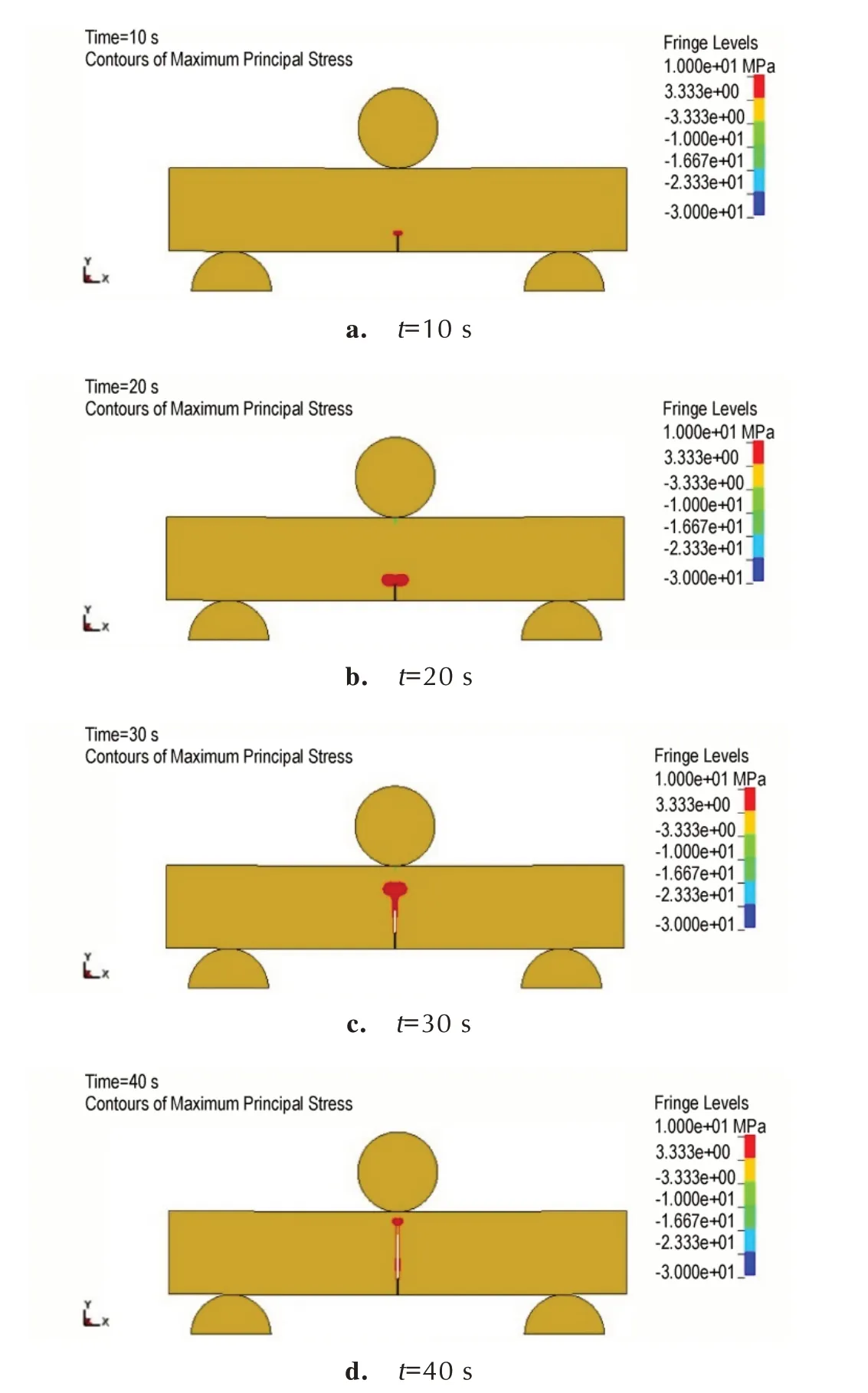
图2 初始裂缝长度2 mm，炸药样品中的应力变化云图和裂缝演化过程Fig.2 Contours of principal stress and crack in explosives with an initial crack length of 2 mm

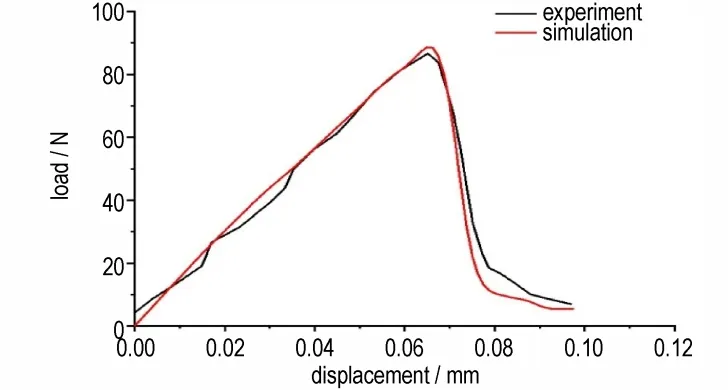
图3 初始裂缝长度2 mm，荷载随炸药样品位移变化曲线Fig.3 Load-displacement curve for specimen with an initial crack length of 2 mm

图4 显示了不同初始裂缝尺寸情况下荷载随样品位移变化的曲线，并且将计算结果与试验结果进行了对比，实线是数值模拟结果，虚线是相应的试验结果。表2 列出了计算获得的起裂荷载与试验结果的对比情况，两者符合较好，这些结果进一步校验了计算模型和失效判据的有效性。同时，还可以看出，在三点弯曲试验中，对于不同初始裂缝尺寸的样品，起裂荷载随着初始裂缝尺寸的增加而减小。

表2 起裂荷载计算值与试验结果［6］比较Table 2 Comparison of load magnitude predictions with experiments

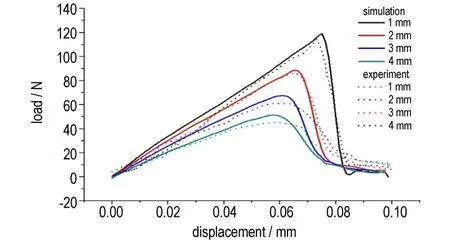
图4 不同初始裂缝尺寸，荷载随炸药样品位移变化曲线对比Fig.4 Load-displacement curves for specimens with different initial crack lengths

2 炸药裂缝扩展过程的影响因素分析

在服役环境中，复杂装药结构中炸药受结构约束的影响，外界刺激引起的炸药受力状态很复杂，与约束结构密切关联，进而裂缝的产生及其扩展问题非常复杂，特别是三维结构内的损伤破坏机制和演化规律很难分析，因为炸药是非透明材料，无法直接观察其内部的裂缝扩展情况。因此，本研究选取三点弯曲试验作为对象，重点开展加载条件的影响规律分析，一方面可以简化约束结构，另一方面在支撑柱位置又能反映局部应力集中现象，从而更清晰地认识裂缝产生和扩展机制。

通过大量的数值模拟工作，我们认识到加载速率和加载位置等关键因素，对炸药裂缝扩展演化过程存在较大的影响。为了分析这些重要因素的影响，设计了一系列计算模型，获得了样品起裂荷载等物理量的变化曲线，裂缝产生和演化过程的图像，着重分析了加载速率和加载位置对裂缝扩展和断裂模式的影响。

2.1 加载速率和加载位置与起裂荷载之间的关系

在前文，载荷施加位置和初始预制裂缝都是在样品梁中间，样品起裂和裂缝扩展过程都发生在样品中间。为了进一步分析加载位置和加载速率对样品裂缝扩展演化过程的影响，将加载圆柱体移动至初始预制裂缝与支柱中间的位置，加载方向不变，设计了不同加载速率的计算模型进行数值模拟分析。为此，研究分别针对加载位置在样品中间和偏离初始裂缝位置的情况，考察了加载速率对起裂荷载的影响，计算模型中样品的初始裂纹长度为1 mm，加载速率v为1.0，2.5，5.0 m·s-1和10.0 m·s-1，模拟结果如图5、6 所示。图5为样品起裂荷载随加载速率变化曲线，模型1 对应加载位置位于样品梁中间，模型2 对应加载位置在初始预制裂缝和支柱的中间。由图5 的数值计算结果表明，随着加载速率增大，起裂荷载也不断增大；而对于同一加载速率情况，加载位置在样品中间时，起裂荷载相对较小，这是因为支柱的支撑力在裂缝位置产生了更大的力矩作用。

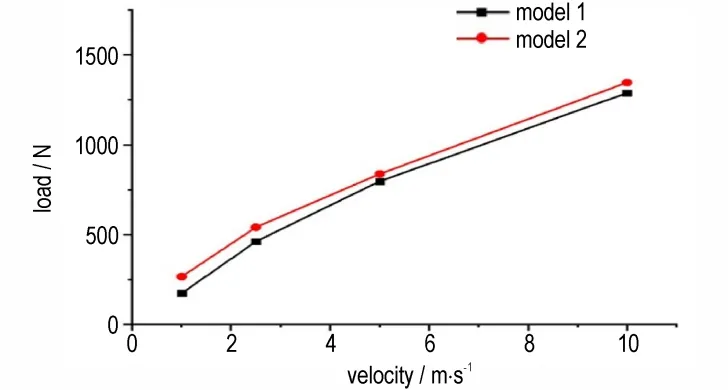
图5 样品起裂荷载随加载速率变化曲线Fig.5 Load magnitude variation curves for different loading rates

图6 为模型1 中裂缝尖位置最大主应力的变化过程，当加载速率是1.0 m·s-1时，裂缝尖位置的应变率约6000 s-1，而 加 载 速 率 是10.0 m·s-1时，应 变 率 约28000 s-1，可以看出，随着加载速率的增加，应变率增大，样品中的最大主应力逐渐增大，这反映了PBX 炸药样品存在应变率效应。

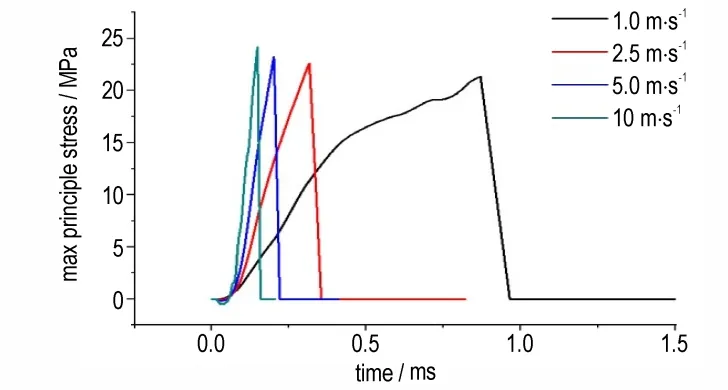
图6 不同加载速率下，炸药裂缝尖位置最大主应力的变化过程Fig.6 Curves of maximum principal stress at the crack tip for different loading rates

2.2 加载速率和加载位置对炸药裂缝扩展演化过程的影响

为深入分析炸药裂缝扩展演化过程与加载速率和加载位置之间的关系，针对加载位置在初始预制裂缝与支柱中间的情况（即偏离初始裂缝位置的情况），数值模拟了一系列典型加载速率下裂缝扩展演化过程。图7a～7d 显示了不同加载速率情况下炸药样品中损伤和裂缝扩展过程的数值模拟图像，图7a～7d 依次表示加载速率v为0.25，2.5，5.0 m·s-1和10.0 m·s-1的数值模拟图像。由图7 可以看出，加载位置偏离初始裂缝位置时，初始裂缝位置、加载位置和支撑位置都会产生应力集中效应，容易发生塑性变形、失效损伤或断裂破碎，但是对于不同加载速率情况，样品中的裂缝扩展演化过程差异很大，产生了4 种破坏模式：

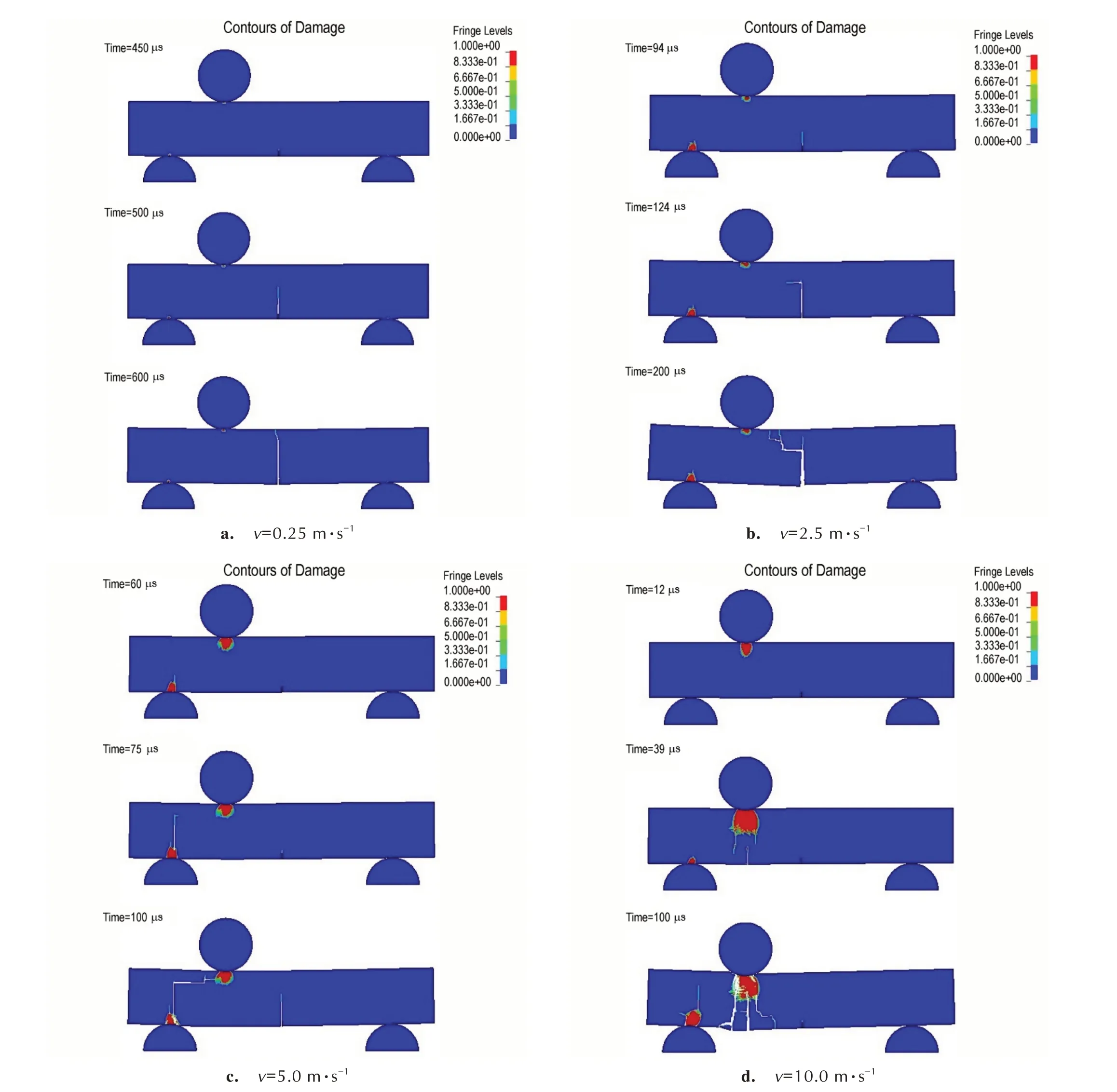
图7 不同加载速率情况，炸药样品起裂和裂缝扩展演化过程Fig.7 Evolution process of crack initiation and development in specimens for different loading rates

（A）当加载速率0.25 m·s-1，较低时（图7a），样品上受到的荷载较小，由于初始裂缝位置的拉应力先达到了抗拉强度，产生拉伸破坏，能量释放主要沿着初始裂缝进行，于是裂缝也在这位置沿着原方向继续扩展，即加载速率较低时候，初始缝隙等因素起主导作用，产生拉伸开裂模式；

（B）随着加载速率增大至2.5 m·s-1（图7b），加载位置的应力也增加，使得裂缝扩展方向会向加载位置偏移，产生裂缝路径弯曲扩展模式；

（C）进一步增大加载速率，至5.0 m·s-1（图7c），样品与支撑圆柱接触位置由于受到较大的压应力作用，会达到抗压强度而产生压缩破坏，同时这个位置附近也受到较强的拉应力而发生拉伸破坏，因此除了在样品中间初始裂缝位置扩展外，在支柱位置也会产生新的损伤和裂缝，即在约束条件和初始缝隙共同作用下，产生多裂缝扩展模式，初始裂缝位置继续拉伸开裂，强约束位置发生压缩破碎后产生新的裂缝扩展；

（D）加载速率更大的情况，为10.0 m·s-1（图7d），除了支柱位置产生新的裂缝扩展外，由于加载位置受到了较强的冲击载荷作用，该位置附近的拉压应力也会迅速超过破坏强度，发生断裂破碎、产生新裂缝，并且迅速扩展直至样品断裂，即加载速率较高时，外载荷和强约束起主导作用，产生动态断裂破碎模式，大部分能量释放主要发生在加载位置和强约束位置附近的局部区域。

上述现象体现了在内因（系统结构）和外因（加载速率）竞争情况下，典型动力学系统的响应特征演化和模式演化。在较低的加载速率范围内，系统响应呈现内因主导模式，即模式A，准静力学响应特征明显，从预制的初始裂缝处开始动态扩展过程，裂缝轨迹基本不变。而在较高的加载速率下，系统响应呈现外因主导的强动力学响应模式（模式D），伴随较高的加载速率，系统的能量急剧增加、超过承受阈值，此时需要更快的能量释放模式，主要特征：一是局域性，体现在加载位置处样品的破碎，而预制的初始裂缝不会扩展；二是灾变性，在加载位置处呈现多条裂缝同时扩展的断裂现象，产生与外因主导强动载、系统能量激增相匹配的能量快速释放机制。

模式B 和模式C 为过渡模式，内因和外因均发挥不可忽略的作用，体现了内因主导模式A 和外因主导模式D 的混合特征。在模式B 中，裂缝扩展具有模式A 的“记忆”效应，早期阶段裂缝扩展从预制裂缝处开始，沿着内因主导的预定轨迹扩展，后期阶段裂缝偏离预定轨迹，向着加载点方向演化，裂缝扩展呈现弥散特点。在模式C 中，除了内因主导的初始预制裂缝扩展外，外因主导在左支撑点和加载点两个位置处产生了新的应力集中点，两个位置处产生的裂缝不断扩展、直至贯通，是能量的主要释放过程，而初始裂缝最终停止扩展，较好地体现了模式C 是由早期的主导模式A 向后期的主导模式D 过渡的演化特征。

总的说来，加载速率较小时，初始裂缝对材料断裂破坏过程的影响较大，而随着加载速率增加，初始裂缝的影响减弱，加载条件和约束条件的影响增强。

3 结论

本研究围绕加载条件对炸药缝隙扩展过程影响问题，基于钝感炸药的三点弯曲试验，采用RHT 材料模型，结合多种模式组合的失效判据，开展了炸药起裂和裂缝演化过程的数值模拟研究，拟合标定了主要的计算参数，校验了计算模型及其适用性。

数值模拟分析了初始裂缝尺寸、加载速率和加载位置对炸药裂缝扩展演化规律的影响，研究结果表明：

（1）随着加载速率增大，起裂荷载增大，而初始裂缝尺寸和加载位置对炸药裂缝扩展演化的影响减小；

（2）加载位置偏离初始裂缝位置时，对于不同加载速率情况，样品中的裂缝扩展演化过程差异很大，随着加载速率的增加，样品的破坏存在4 种模式，从准静态裂缝拉伸开裂向动态断裂破碎模式转变，这反映了初始裂缝等内因主导模式向约束和载荷等外因主导模式演化的动力学响应特征。

另外，本研究针对工程应用的研究需求开展建模分析，获得不同加载速率下的裂缝扩展路径，主要反映了定性规律，而真实的裂缝情况更加复杂，也跟材料非均质的微结构相关。