适用于复杂拓扑结构混合直流电网的实用机电暂态建模仿真方法
吴国旸,戴汉扬,宋新立,李 慧,苏志达,李霞
适用于复杂拓扑结构混合直流电网的实用机电暂态建模仿真方法
吴国旸1,戴汉扬1,宋新立1,李 慧2,苏志达1,李霞1
(1.中国电力科学研究院有限公司,北京 100192;2.北京信息科技大学,北京 100192)
为提升混合直流输电系统模型的适应性和计算效率,提出一种基于电流源思想的混合直流输电系统机电暂态建模方法。由电网换流器(line commutated converter, LCC)、电压源换流器的准稳态模型推导其电流源模型,并通过差分化直流支路的微分方程,形成直流电网的通用化电流源模型。采用多速率混合积分算法分别求解交直流系统,并结合步长回退、积分方法切换等,解决LCC电流反向、开关闭合与开断等特殊情形下的数值问题。在国内通用的机电暂态仿真程序中实现了上述模型,并以白鹤滩-江苏混合直流输电工程为例,与电磁暂态仿真工具进行了对比测试。仿真结果验证了该方法的有效性和准确性。该方法较好地平衡了仿真精度和计算速度的矛盾,为提升大规模交直流混联电网的仿真能力提供了有力工具。
混合直流;机电暂态;建模;电网换相换流器;电压源换流器
0 引言
近年来,为了满足大容量远距离送电、大规模新能源并网和孤岛送电等需求,不同形式的直流输电技术在我国得到了快速发展,多电源供电、多落点馈入,涉及不同类型换流器的多端直流、混合直流已成为业界广泛关注的热点[1-2]。其中,基于电网换相换流器(line commutated converter, LCC)的传统直流输电技术经过多年的发展,具有成本低、技术成熟的优势[3];而基于电压源换流器(voltage source converter, VSC)和模块化多电平换流器(modular multilevel converter, MMC)的直流输电技术(为行文方便,以下统称VSC),具有控制调节性能优良、组网结构灵活的特点;混合直流则兼具两者优点,有效扩展了直流输电系统的适用范围,具有十分广阔的应用前景[4-5]。
混合直流输电技术作为一种新兴的直流输电技术,其相关研究主要集中在电磁暂态领域,侧重于研究直流保护[6-9]、故障穿越[10-11]及其他控制保护策略[12-15]。由于计算速度和仿真规模的限制,现阶段电磁暂态仿真尚不适合用于大规模交直流电力系统的稳定计算[16],机电暂态仿真软件仍然是电网调度运行、规划设计进行暂态稳定分析的主要手段。
目前,LCC-VSC型混合直流系统机电暂态建模方面的文献相对较少[17-19]。文献[17]提出了LCC-VSC混合直流系统的建模方法,在 PSASP程序中实现了自定义建模,并对模型在交流系统故障中的动态响应进行了分析。文献[18]在建立混合直流系统的机电暂态模型时,计及了MMC桥臂电感对直流侧电路的影响,并提出了相应的潮流计算方法。文献[19]建立了直流网络的等效电路模型,提出了多端直流系统各换流站控制系统之间的相互协调机制。但上述文献未涉及耗能电阻等新设备和直流系统内部故障,也未考虑混合直流求解过程中电流反向、换相失败等特殊情形的处理。
与传统两端直流相比,多端直流呈现出拓扑结构和运行特性复杂化的趋势。一方面,电网中相继出现了串联或并联形式的LCC多端直流和VSC多端直流,乃至同时接入LCC换流器和VSC换流器的混合直流输电系统;另一方面,随着直流断路器、避雷器和耗能电阻等新技术的相继应用,多端直流输电系统的动态特性也变得更加复杂。然而,现有机电暂态仿真工具缺少通用化的多端直流输电模型,难以满足电网建设运行和直流技术发展的需求。为了准确掌握电网中不同类型直流输电系统的动态特性,必须深入研究适于大规模交直流电网稳定计算的混合直流建模仿真方法,在兼顾效率和精度的基础上,建立准确的混合直流电网实用模型。
本文提出了一种基于电流源思想、适用于具有复杂拓扑的混合直流网络通用化建模仿真方法,即:将直流电网中的换流器、直流线路、平波电抗器和电容等设备和元件,均视为独立的电流源,分别进行建模,并基于现有成熟LCC和VSC详细控制系统模型[20],在国内主流机电暂态仿真程序PSD-BPA中实现了通用的混合直流网络模型,最后利用电磁暂态仿真程序验证了其正确性。
1 直流网络建模
为了提升直流输电系统模型的适应性和计算效率,克服现有机电暂态仿真程序只能面向固定拓扑直流建模,难以适应未来可能出现的复杂拓扑直流系统的缺陷,本文基于电流源思想,将任意形式直流电网中的换流器、直流线路、平波电抗器和电容等设备和元件,均视为独立的建模对象,分别建立各自的微分方程;通过差分化微分方程组,形成所有对象的等效电流源与并联导纳;以支路和节点为拓扑索引,形成直流网络节点导纳阵,最终计算得到直流电压和其他电气量。
1.1 换流器模型
实际直流输电系统中LCC换流器或VSC换流器的结构非常复杂,但对于电网机电暂态仿真而言,主要关注其外特性。为降低仿真系统的规模,提高仿真效率,本文采用准稳态模型和集总参数[21],并将换流器视为一个多端口网络,根据输入输出特性,将其等效为受控电流源或电压源。下面以LCC换流器为例,进行详细说明。类似地,也可以得到VSC换流器的电流源模型。


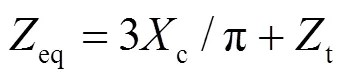

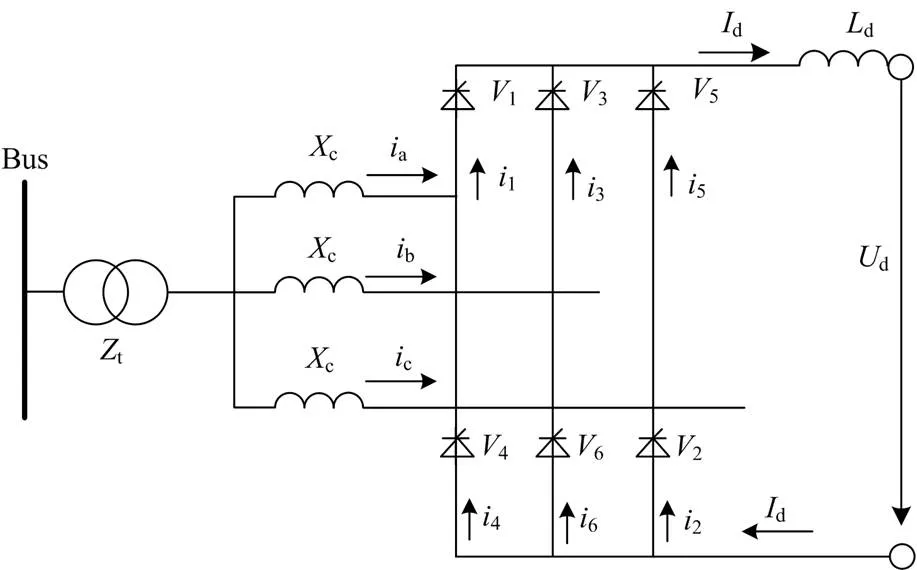
图1 LCC换流器电路示意
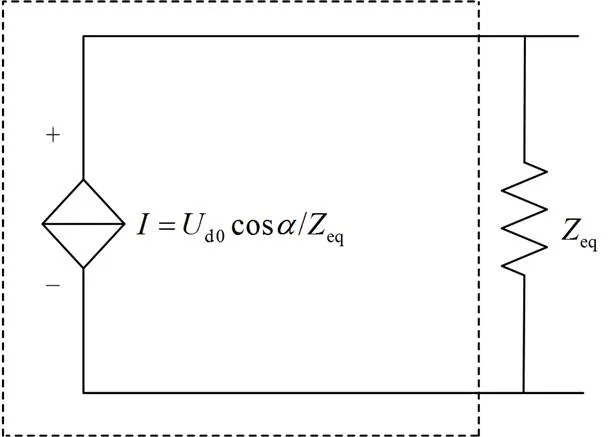
图2 LCC换流器等效电流源
1.2 支路模型
直流网络中的支路可分为两类:一类为包括线路、电容和电感等参数不变的普通定阻抗支路;另一类为涉及故障或操作的变阻抗支路。下面分别进行讨论。
1.2.1定阻抗支路

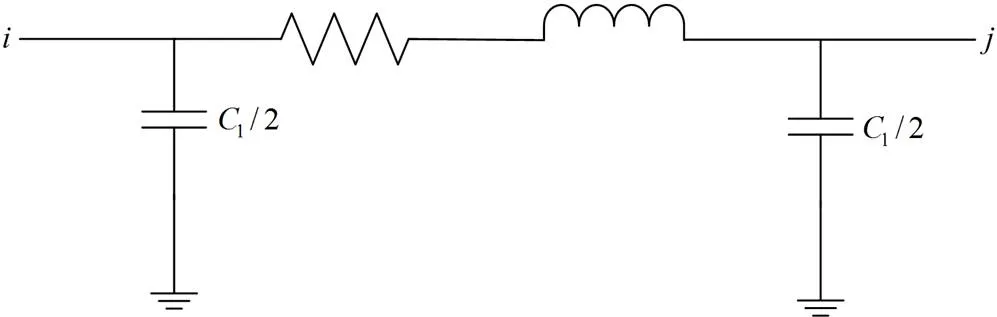
图3 直流输电线路模型

图4 直流线路电流源模型


1.2.2变阻抗支路
除了1.2.1节所述的定阻抗支路,直流网络中还存在一些特殊情形,需要采用变阻抗支路的形式进行处理,如直流线路短路、耗能装置动作以及电流反向等。
直流线路短路是直流仿真中一种常见的故障操作。短路支路与前述定阻抗支路具有相同的形式,但前者只存在于短路故障期间。当直流电网发生故障时,短路点将原支路分割成两部分,短路支路的另一侧为地或另一条支路上的某一点。据此推广,可在真双极、伪双极等各种形式的直流网络中,方便地模拟任意地点、任意重数的直流线路之间的短路或者直流线路对地短路等故障。图5给出了直流线路经RL支路短路的示意图。
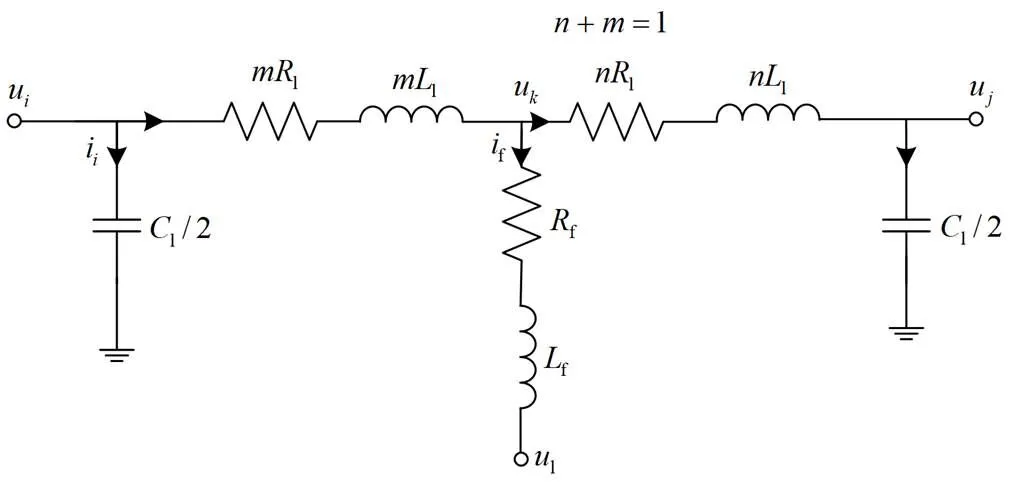
图5 直流线路经RL支路短路
混合直流电网往往还配置了直流耗能装置和避雷器等快速动作的设备。这些设备的控制策略较为复杂,但在原理上也将其视为可变阻抗支路。因此,仍然可以采用阻抗支路模型对其建模。由于这些设备的投退状态变化极快,仿真过程中可能需要反复、快速修改其阻值,相应的数值积分方法必须采用足够小的步长。
此外,还有一类可变阻抗支路是由换流器自身特点引起的,例如LCC换流器的电流反向、换相失败和换流器闭锁等问题。一般而言,仿真中出现上述问题时,可将相应支路的阻抗值设为无穷大或0,从而改变相应支路的开断与导通状态。由于混合直流的拓扑结构较为复杂,必须结合换流器所在位置和接入方式对支路的等值阻抗进行修改,以免造成计算结果异常。本文3.2节、3.3节将进一步讨论与此相关的积分算法问题。
2 直流输电控制系统建模
混合直流输电系统基于LCC和VSC控制系统实现对直流电流、直流电压的控制。目前,国内主流机电暂态仿真程序PSD-BPA、PSASP均已开发出较为成熟的LCC和VSC详细控制系统模型[17,20]。
在基于LCC的直流控制系统方面,有限幅型和选择型两种技术路线。其中,限幅型直流输电控制系统的机电暂态模型[15]已在国内得到广泛应用,而选择型直流输电控制系统尚缺乏相应的详细模型,本文主要针对后者进行建模。选择型直流输电控制系统包括电流指令计算、低压限流、关断角控制和闭环控制器等重要功能模块。
2.1 电流指令计算
图6为电流指令计算模型。在定功率模式下,可根据功率参考值和直流电压,计算得到相应的电流指令;而在定电流模式下,该指令则取所设定的电流参考值。

图6 电流指令计算模型
2.2 低压限流
低压限流环节根据预先设定的特性曲线,通过对故障时的电流指令值进行限幅,增加直流系统的抗扰动能力和故障恢复能力,控制逻辑如图7所示。

图7 低压限流模型
2.3 关断角控制
关断角控制对维持直流输电系统的安全稳定性至关重要。该模块根据换相理论预测逆变侧的关断角,并通过控制其大小来防止换相失败的发生,模型如图8所示。
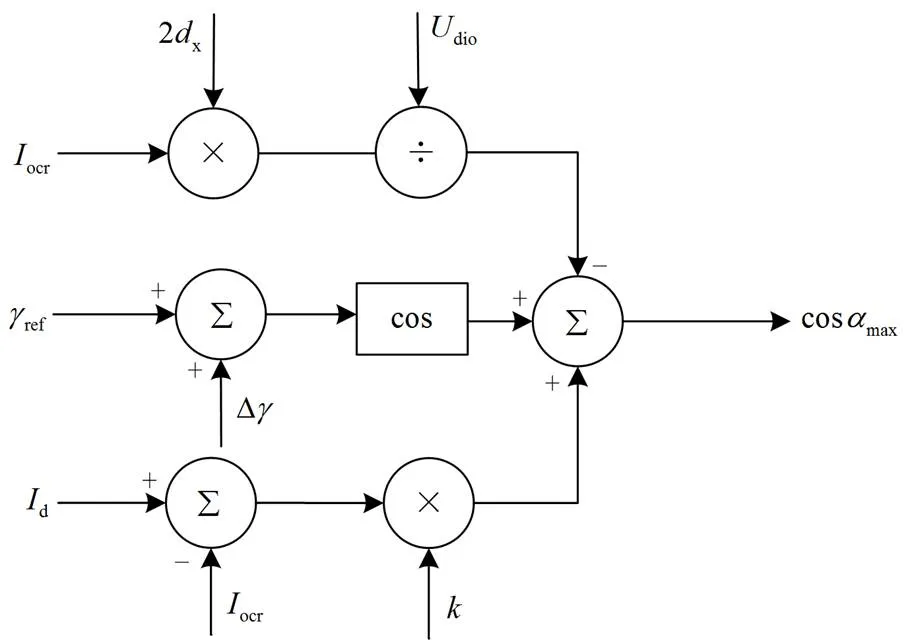
图8 关断角控制模型
2.4 闭环控制器
闭环控制功能由一个PI控制器实现。PI控制器对输入的直流电压和直流电流的误差进行比较,在整流侧选择误差小者作为输入,逆变侧则选择误差大者作为输入。该设计的优点是可以实现控制器之间的无扰动切换,避免了切换时的控制死区和对系统的扰动。图9给出了闭环控制器模型的控制逻辑图。其中,输出部分的下限值取自图8中关断角控制模型的输出。

图9 闭环控制器模型
3 直流网络数值积分算法
直流输电控制系统的机理较为复杂,响应速度很快。与常规机电暂态模型相比,直流输电模型阶数高、响应快、计算量大,对求解效率和精度要求高,其仿真步长将受到严格约束。因此,相应的数值积分方法除具有良好的数值稳定性和收敛性之外,还应具有较高的仿真效率。
3.1 多速率混合积分算法



本文将整个目标仿真系统划分为快速变化与慢速变化两类子系统。其中,快变系统(例如,直流输电系统、电力电子设备等)的时间常数小,动态过程速度快;而慢变系统(例如,常规机组的原动机和调速系统)具有相对较大的时间常数,动态过程速度较慢。
为了兼顾仿真精度和计算速度,两类系统宜分别采用不同的积分速率。其中,以慢变系统为主导的整个电力系统仍以正常机电暂态积分步长进行计算,而快变系统则以此步长为基础,平均划分为若干小步长进行积分,采用隐式梯形法进行迭代计算。
快变系统各时步所需外部输入变量由慢变系统经线性插值得到,并在慢变系统步长结束时,将计算结果回送至慢变系统。因一个慢变步长内交流电网的电压电流保持不变,快慢系统只有代数量耦合,积分的收敛性由隐式梯形法及给定的步长保证。快慢系统的交替迭代在每个仿真步需要多次迭代,以消除交接误差。
图10为包含混合直流模型的多速率混合数值积分方法示意图。由于直流输电控制保护系统功能复杂,间断环节多,本文算法在积分过程中考虑了相应的步长回退问题,以便在保护动作或者执行间断环节的不同分支时,放弃本步长,重新积分。需要说明的是,3.2节、3.3节所采用的方法均基于本节算法。

图10 多速率混合数值积分算法示意图
3.2 开关开断处理
直流输电系统目前主要依靠换流器移相、闭锁或者开断交流侧开关对故障进行隔离。随着直流电网的引入,直流开关的应用将成为趋势。本文直流电网求解采用机电暂态仿真中最常用的隐式梯形法。但当开关操作使电感两端压降或流过电容的电流产生突变时,可能会出现数值振荡现象[23]。
机电暂态算法的高效性很大程度上依赖于定步长仿真,然而,这些开关器件的开通和关断并不一定在这些固定间隔的时间点上。因此,固定的步长不能准确地描述这些开关过程。不失一般性,图11给出了定步长积分算法条件下,在非过零点开断电感支路时的电流电压变化曲线。
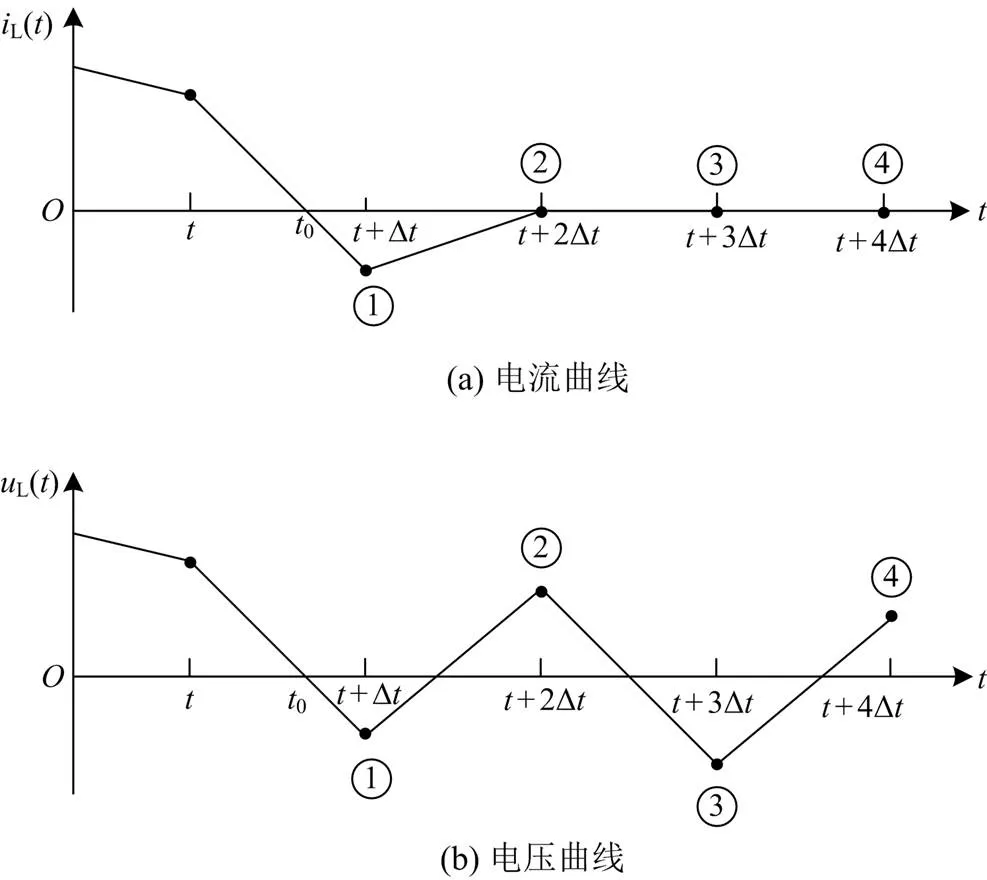
图11 开关断开电感支路电流和电压曲线

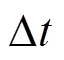
3.3 LCC换流器电流反向处理
机电暂态仿真中的换流器模型通常较为简单,主要关注其外部特性。一般而言,这是一种简单、有效的等效方式,但却不能体现LCC换流器单向导通的特性。例如,在换相失败、重启动等异常工况下,换流器及相应的阻抗支路模型可能出现实际设备并不存在的电流反向问题。为了避免仿真结果失真,以往点对点的直流模型中,当出现电流反向时,往往采取直接置零的方式解决。但混合直流的拓扑结构复杂,无法简单地套用这种处理方式,而需要通过插值的方法找到电流过零点,并注意避免数值问题。
在机电暂态仿真中,通常采用定步长的积分求解算法,但是LCC换流器的电流反向与恢复的过零点,却不一定正好落在积分点上。因此,需要通过插值的方法找到电流过零点。

图12 电流反向插值算法



4) 恢复正常步长,继续积分。
换流阀的恢复导通需要根据换流器类型进行判别。以图13所示混合直流等效电路为例进行说明。对于整流侧换流器LCC1来说,只有等效电势大于端电压时,换流阀才能恢复导通;而对于逆变侧换流器LCC2,则当端电压大于等效电势时,换流阀才能恢复导通。在拓扑复杂的混合直流电网中,只有当该换流器所在通路上的所有LCC换流器均满足导通条件时,才能认为换流阀恢复导通,否则可能会导致数值问题。具体步骤与电流反向类似,所不同的是,每一步积分前,要先判断换流器所在通路是否导通,然后再修改导纳阵,重新积分。
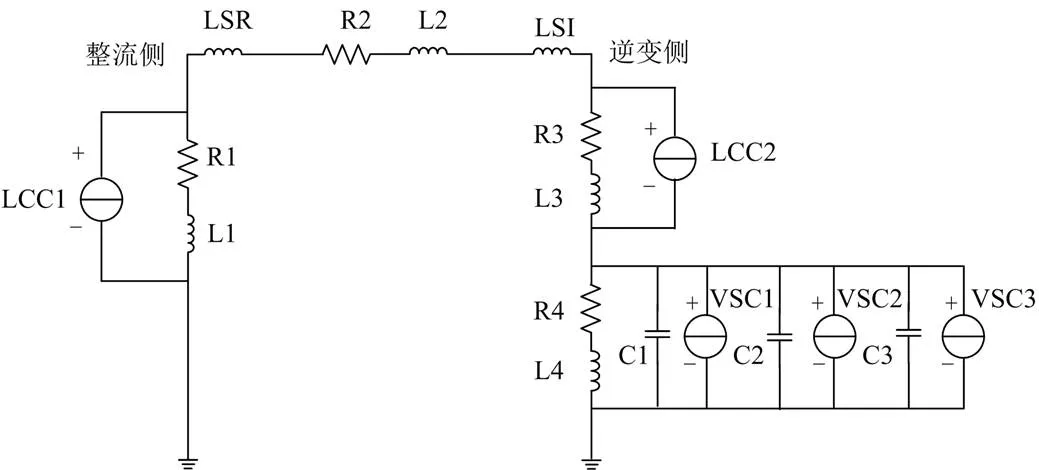
图13 混合直流等效电路示意
实际上,LCC模型的换相失败、耗能装置投切等也有类似问题,同样涉及较为复杂的过程。但由于直流电网的规模均不大,即便多次修改导纳阵,也不会造成计算量的显著增加。
4 仿真算例
为了验证本文模型和算法的正确性,采用国家电力调度通信中心电磁暂态日常计算工具PSD- PSModel的仿真结果作为参考,验证PSD-BPA机电暂态模型的计算结果。基于同一算例,在初始潮流以及控制器基本一致的情况下,对比测试典型故障情况下,机电暂态程序PSD-BPA以及电磁暂态程序PSD-PSModel的动态响应特性是否基本吻合。并在此基础上,进一步对比分析PSD-BPA原有积分算法,验证本文方法的有效性。
4.1 算例简介
算例电网建立了白鹤滩-江苏±800 kV LCC-VSC双极多端混合直流输电系统的机电暂态模型。为便于说明,图14给出了其中一极的等值系统结构,并用等值换流器对相应换流站进行等效。其中,G1—G5分别表示各交流等值系统,T1—T5分别为各换流变压器,LINE1—LINE4则表示相应直流线路,整流侧为LCC换流器,逆变侧采用分层接入结构,高端为LCC换流器,低端为3个并列的VSC换流器。

图14 白鹤滩-江苏混合直流等值系统结构图
算例中,各交流系统额定电压均为525 kV,整流侧换流器LCC1的直流额定电压为±800 kV,逆变侧换流器LCC2和VSC1—VSC3的直流额定电压均为±400 kV,换流器LCC1采用定功率控制,LCC2采用定电压/定熄弧角控制,低端3个VSC换流器中,VSC1为运行于定电压控制模式的平衡站,电压参考值为400 kV,VSC2和VSC3则采用定功率控制模式。显然,逆变侧所有换流器均处于受电状态,仿真时间为10.0 s。
本节通过对比PSD-BPA和PSD-PSModel的仿真结果,分析本文混合直流模型的动作特性。
由图14可以看出,本算例送端系统与常规特高压分层直流完全相同,混合直流的特点主要体现在受端系统,因此,算例着重分析受端相关情形。
4.2 逆变侧高端交流系统三相短路故障
稳态时,LCC1送出有功4000 MW,相应地,LCC2吸收有功1883 MW,VSC2、VSC3分别吸收功率667 MW,剩余功率由VSC1平衡。1.3 s时,逆变侧交流系统在换流变T2附近发生三相短路故障,1.4 s故障清除。图15—图17分别给出了整流侧和逆变侧高、低端换流器的直流电流、电压响应曲线。


图16 逆变侧高端仿真曲线

图17 逆变侧低端仿真曲线
对比所建立的机电模型和电磁模型仿真波形,两者的暂态过渡过程虽有一定差异,但总体而言,机电模型能够较好地反映电磁暂态仿真的动态响应趋势。出现上述差异的原因主要是在机电暂态仿真中,对换流阀、锁相环和一些快速响应的复杂控制环节做了简化处理,采取了等效建模手段[24];此外,机电暂态仿真也未能考虑负序、谐波等因素的影响。
4.3 逆变侧低端交流系统三相短路故障
在1.3 s时,逆变侧交流系统在换流变T4近区发生三相短路故障,1.4 s时故障清除。图18—图20分别给出了换流器LCC1、LCC2和VSC1的响应过程。

图18 整流侧仿真曲线
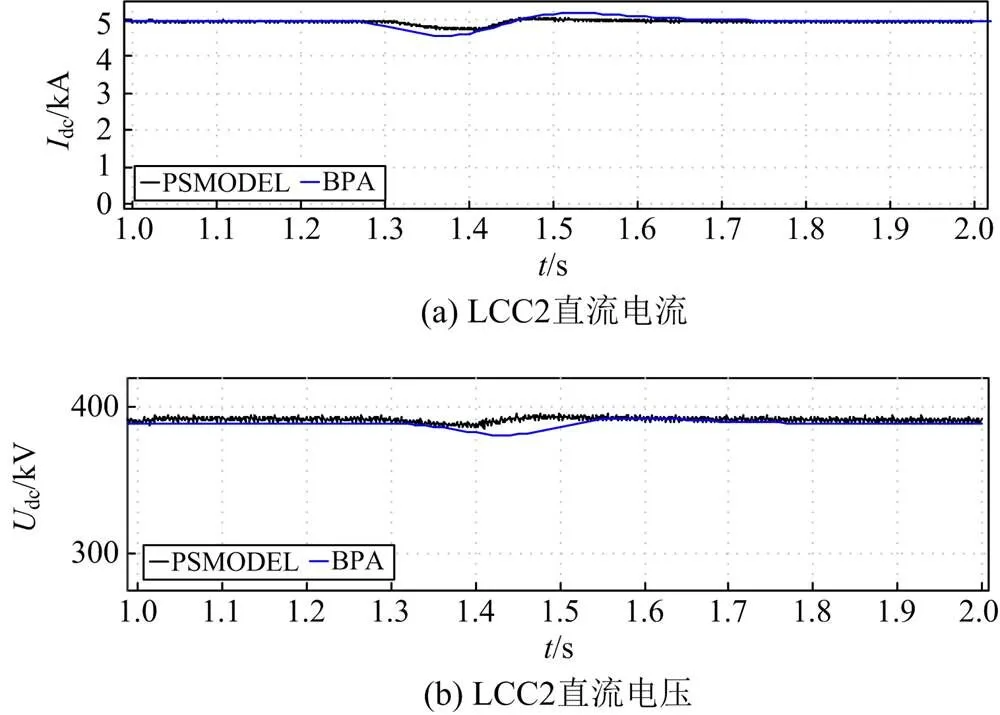
图19 逆变侧高端仿真曲线

图20 逆变侧低端仿真曲线
由仿真曲线可以看出,相比于4.2节的逆变侧高端交流系统故障,VSC换流器交流侧故障后,两者的响应曲线吻合得更好。
其主要原因是LCC和VSC的换流器直流电压建立方式不同。前者直流电压受交流电压的直接影响,因此变化较为显著;而VSC的直流电压则体现了能量的累积作用,特别是定电压站,本身具有一定的调节能力,降低了交流系统故障对直流系统的冲击。
4.4 直流系统重启动故障
在3.5 s时,直流线路近逆变侧发生短路故障,4.5 s时故障清除。直流系统发生3次重启动,并在第3次重启动成功。图21—图23为重启动故障时BPA模型和PSMODEL模型仿真波形对比。
可以看出,两种仿真工具计算结果的差异较4.2节、4.3节明显。这是由于直流系统内部发生故障,冲击更为显著。另一方面,电磁模型更为详细,并计及了负序和谐波等因素的影响,因此在恢复过程中,会出现剧烈的振荡和毛刺,同时恢复过程相对较慢;而机电模型由于前文所述原因,响应曲线较为光滑,状态量的恢复也更为迅速。但总体而言,BPA机电模型仍然能够较好地反映实际直流输电系统的动态响应趋势。

图21 整流侧仿真曲线
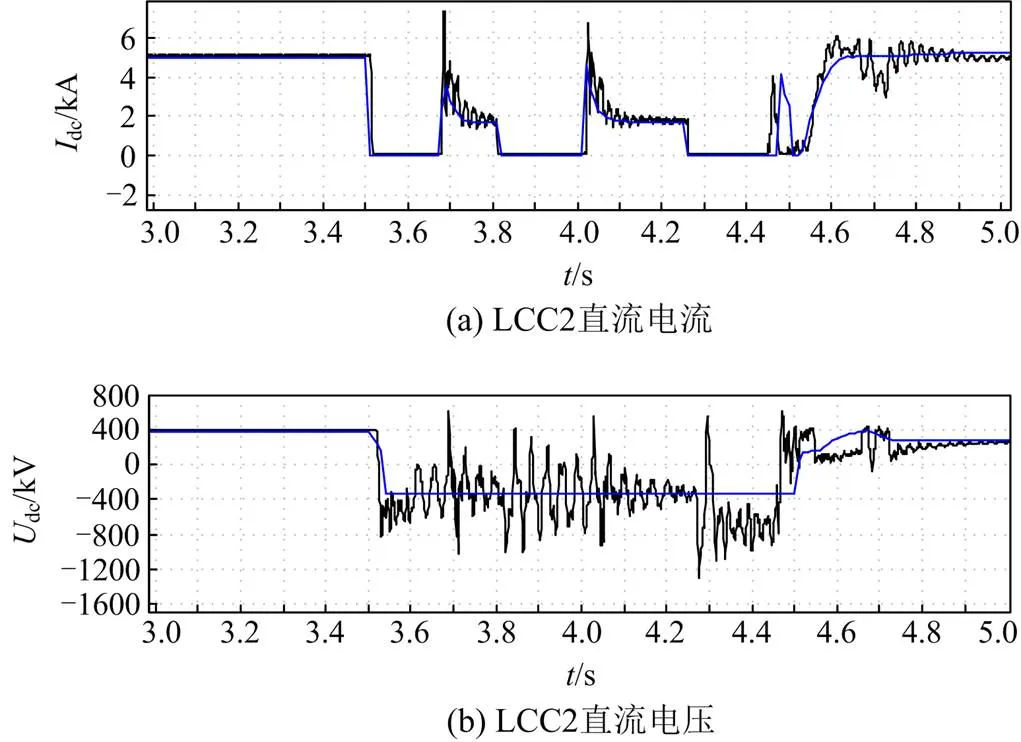
图22 逆变侧高端仿真曲线

图 23 逆变侧低端仿真曲线
4.5 多速率混合积分算法分析
为了验证多速率混合积分算法,本节仍以4.2节逆变侧交流三相短路故障为例,对不同算法组合的效果进行了对比分析。
为了减小稳态情形对误差结果的影响,误差分析仅针对故障开始瞬间至故障结束后200 ms内的状态变化,并以PS-MODEL仿真结果作为基准,采用平均值误差进行计算。表1给出了采用不同算法的计算耗时与误差分析。

表1 多速率混合积分算法效果分析
其中,算法1、算法2分别采用10 ms和50ms的交、直流系统统一步长;算法3—算法5则采用混合积分算法,相应的直流系统小步长分别为500ms、50ms和10ms,交流系统大步长则均为10 ms。表1中计算耗时为纯计算时间,不含程序输入输出及初始化耗时。
由表1可见,采用混合积分算法可显著提高计算效率,且仿真精度与采用50ms小步长时的隐式梯形法十分接近;直流系统小步长选取50ms与10ms时,精度差别不大,均可以满足稳定计算要求,但计算耗时差距较大。其他故障情形下虽然具体数值略有偏差,但总体效果类似,不再赘述。
一般而言,较小的步长通常迭代次数也较少,因而耗时较为接近。考虑到直流换流器0.5~1 ms的开关动作时间,实际计算中可选取50~250ms作为混合积分算法的小步长。
5 结论
本文系统阐述了在大规模电网稳定仿真中建立LCC换流器、VSC换流器和直流网络的机电暂态模型及积分求解的实用方法。通过与PSD- PSModel中搭建的电磁暂态模型进行算例对比,验证了模型和算法的有效性和准确性。仿真结果表明:
1) 对于交流系统故障而言,PSD-BPA机电暂态模型与PSD-PSModel电磁暂态程序计算结果一致,相关状态量主体特征基本吻合。
2) 对于直流系统故障而言,PSD-BPA机电暂态模型与PSD-PSModel电磁暂态程序在故障发生侧的响应差异稍大,但总体响应趋势基本一致。
3) PSD-BPA机电暂态模型与PSD-PSModel电磁暂态程序的仿真结果存在一定差异。这是因为在机电暂态仿真中采用基波正序向量模拟换流阀,不考虑其电磁过程,且对控制系统进行了聚合、替代和有效值等值等简化处理。
本文建立了包含LCC换流器、VSC换流器的直流电网实用模型,在国内通用的机电暂态仿真程序中实现了具有复杂拓扑的混合直流输电系统的通用化模拟,为提升大规模交直流混联电网的仿真能力提供了有力的工具。
[1] 王永平, 赵文强, 杨建明, 等. 混合直流输电技术及其发展分析[J]. 电力系统自动化, 2017, 41(7): 156-167.
WANG Yongping, ZHAO Wenqiang, YANG Jianming, et al. Hybrid high-voltage direct current transmission technology and its development analysis[J]. Automation of Electric Power Systems, 2017, 41(7): 156-167.
[2] 饶宏, 洪潮, 周保荣, 等. 乌东德特高压多端直流工程受端采用柔性直流对多直流集中馈入问题的改善作用研究[J]. 南方电网技术, 2017, 11(3): 1-5.
RAO Hong, HONG Chao, ZHOU Baorong, et al. Study on improvement of VSC-HVDC at inverter side of Wudongde multi-terminal UHVDC for the problem of centralized multi-infeed HVDC[J]. Southern Power System Technology, 2017, 11(3): 1-5.
[3] 庄良文, 李亚萍, 周鹏鹏, 等. 直流输电控制与保护系统的工程镜像仿真方法[J]. 电力系统保护与控制. 2021, 49(15): 109-115.
ZHUANG Liangwen, LI Yaping, ZHOU Pengpeng, et al. Engineering mirror simulation method of control and protection system in DC transmission[J]. Power System Protection and Control, 2021, 49(15): 109-115.
[4] GUO Chunyi, CUI Peng, ZHAO Chengyong. Optimization and configuration of control parameters to enhance small-signal stability of hybrid LCC-MMC HVDC system[J]. Journal of Modern Power Systems and Clean Energy, 2022, 10(1): 213-221.
[5] SEYED M A, REZA G. A novel control strategy based on a look-up table for optimal operation of MTDC systems in post-contingency conditions[J]. Protection and Control of Modern Power Systems, 2022, 7(1): 40-50.
[6] 张大海, 杨宇辰, 刘艳梅, 等. 基于EMD与Spearman 相关系数的混合直流线路纵联保护方法[J]. 电力系统保护与控制, 2021, 49(9): 1-11.
ZHANG Dahai, YANG Yuchen, LIU Yanmei, et al. Hybrid HVDC line pilot protection method based on EMD and Spearman correlation coefficient[J]. Power System Protection and Control, 2021, 49(9): 1-11.
[7] XING Chao, LI Shengnan, XI Xinze. Research on a fault location method for a pole-to-pole short-circuit fault in an LCC-MMC Hybrid DC transmission system[J]. IEEE Access, 2020, 8(9): 165683-165692.
[8] LIANG Yuansheng, JIANG Liantao, LI Haifeng, et al. Fault analysis and traveling wave protection based on phase characteristics for hybrid multiterminal HVDC systems[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2022, 10(1): 574-588.
[9] 贾科, 冯涛, 陈淼, 等. LCC-MMC 型混合直流配电系统线路保护方案[J]. 电工技术学报, 2021, 36(3): 656-665.
JIA Ke, FENG Tao, CHEN Miao, et al. Line protection scheme for hybrid LCC-MMC type DC distribution system[J]. Transactions of China Electrotechnical Society, 2021, 36(3): 656-665.
[10] HALEEM N M, RAJAPAKSE A D, GOLE A M, et al. Investigation of fault ride-through capability of hybrid VSC-LCC multi-terminal HVDC transmission systems[J]. IEEE Transactions on Power Delivery, 2019, 34(1): 241-250.
[11] LI Xiaodong, XU Zheng, ZHANG Zheren. Enhanced ride-through capability under rectifier-side AC fault for series LCC-MMC hybrid HVDC system[J]. IEEE Access, 2021, 9: 153030-153057.
[12] RAO Hong, ZHOU Yuebin, XU Shukai, et al. Key technologies of ultra-high voltage hybrid LCC-VSC MTDC systems[J]. CSEE Journal of Power and Energy Systems, 2019, 5(3): 365-373.
[13] ZHANG Zheren, XU Zheng, XUE Yinglin, et al. DC-side harmonic currents calculation and DC-loop resonance analysis for an LCC–MMC hybrid HVDC transmission system[J]. IEEE Transactions on Power Delivery, 2015, 30(2): 642-651.
[14] 彭忠, 孙攀磊, 韩伟, 等. LCC与VSC级联的特高压混合直流输电系统控制策略[J].电力系统保护与控制, 2021, 49(19): 162-172.
PENG Zhong, SUN Panlei, HAN Wei, et al. Control strategy of a hybrid UHVDC transmission system cascaded by LCC and VSC[J]. Power System Protection and Control, 2021, 49(19): 162-172.
[15] LEE G S, KWON D H, MOON S I. DC current and voltage droop control method of hybrid HVDC systems for an offshore wind farm connection to enhance AC voltage stability[J]. IEEE Transactions on Energy Conversion, 2021, 36(1): 468-479.
[16] SHU Dewu, WEI Yingdong, VENKATA D, et al. Cosimulation of shifted-frequency/dynamic phasor and electromagnetic transient models of hybrid LCC-MMC DC grids on integrated CPU–GPUs[J]. IEEE Transactions on Industrial Electronics, 2020, 67(8): 6517-6530.
[17]訾鹏, 赵铮, 陈兴雷, 等. LCC-VSC 混合多端直流输电系统机电暂态建模方法研究[J]. 中国电机工程学报, 2015, 35(24): 6265-6274.
ZI Peng, ZHAO Zheng, CHEN Xinglei, et al. Electromechanical transient modeling of hybrid DC grid based on LCC and VSC converter[J]. Proceedings of the CSEE, 2015, 35(24): 6265-6274.
[18] 肖亮, 王国腾, 徐雨哲, 等. LCC-MMC 混合多端直流输电系统的潮流计算和机电暂态建模方法[J]. 高电压技术, 2019, 45(8): 2578-2586.
XIAO Liang, WANG Guoteng, XU Yuzhe, et al. Methods for power flow calculation and electro-mechanical transient modeling of LCC-MMC hybrid multi-terminal HVDC system[J]. High Voltage Engineering, 2019, 45(8): 2578-2586.
[19] 赵利刚, 洪潮, 涂亮, 等. 多端直流输电系统机电暂态建模研究与实现[J]. 南方电网技术, 2017, 11(7): 26-31.
ZHAO Ligang, HONG Chao, TU Liang, et al. Research and realization of electromechanical transient modeling of multi-terminal DC transmission system[J]. Southern Power System Technology, 2017, 11(7): 26-31.
[20] 中国电力科学研究院. PSD-ST暂态稳定程序用户手册[Z]. (5.7)版. 2020.
[21] 周孝信, 李汉香, 吴中习. 电力系统分析[M]. 北京: 能源部电力科学研究院研究生院, 1989.
[22] 赵婉君. 高压直流输电工程技术[M]. 北京: 中国电力出版社, 2004.
[23] DOMMEL H W.电力系统电磁暂态计算理论[M]. 李永庄, 林集明, 曾昭华, 译. 北京: 水利电力出版社, 1991.
[24] 万磊, 汤涌, 吴文传, 等. 特高压直流控制系统机电暂态等效建模与参数实测方法[J]. 电网技术, 2017, 41(3): 708-714.
WAN Lei, TANG Yong, WU Wenchuan, et al. Equivalent modeling and real parameter measurement methods of control systems of UHVDC transmission systems[J]. Power System Technology, 2017, 41(3): 708-714.
A practical electromechanical transient simulation method for complicated topological hybrid HVDC grids
WU Guoyang1, DAI Hanyang1, SONG Xinli1, LI Hui2, SU Zhida1, LI Xia1
(1. China Electric Power Research Institute, Beijing 100192, China; 2. Beijing Information Science & Technology University, Beijing 100192, China)
To improve the adaptability and computational efficiency of hybrid DC transmission system models, an electromechanical transient modeling method for a hybrid DC transmission system is proposed based on the idea of current source. The current source models of a line commutated converter (LCC) and a voltage source converter (VSC) are derived from their quasi-steady state models, and the general current source model of a DC grid is formed based on the differential equations of DC branches. A multi-rate hybrid integration algorithm is used to solve the AC and DC power systems, and the numerical problems in special cases, e. g., LCC reverse current, breaker closing and opening, are solved by combining integration step rollback and integral method switching. The above model is developed in a domestic general electromechanical transient simulation program. Simulation analysis on the Baihetan-Jiangsu hybrid HVDC transmission system is compared with an electromagnetic transient simulation. It verifies the effectiveness and accuracy of the proposed method, which well balances simulation accuracy and calculation speed, and provides a powerful tool to improve the simulation ability for a large-scale hybrid AC/DC power grid.
hybrid HVDC; electromechanical transient; modeling; LCC; VSC
10.19783/j.cnki.pspc.226431
北京市自然科学基金项目资助(3172015);国家电网有限公司总部科技项目资助“提升直流输电控制系统机电暂态仿真能力的建模研究与开发”
This work is supported by the Beijing Natural Science Foundation (No. 3172015).
2021-12-29;
2022-05-01
吴国旸(1974—),男,通信作者,博士,教授级高工,研究方向为电力系统仿真与分析;E-mail: wugy@epri.sgcc. com.cn
戴汉扬(1989—),男,博士,高工,研究方向为电力系统仿真与分析;E-mail:daihanyang@epri.sgcc.com.cn
宋新立(1971—),男,博士,教授级高工,研究方向为电力系统仿真与分析。E-mail: songxl@epri.sgcc.com.cn
(编辑 许 威)

