面向本地差分隐私的K-Prototypes聚类方法

张国鹏，陈学斌*，王豪石，翟 冉，马 征

（1.华北理工大学 理学院，河北 唐山 063210；2.河北省数据科学与应用重点实验室（华北理工大学），河北 唐山 063210；3.唐山市数据科学重点实验室（华北理工大学），河北 唐山 063210）

0 引言

在网络数字空间中，数据信息的安全与隐私是一个至关重要的问题。数据作为可以进行分配的生产要素，在保证数据公开使用的前提下，用户本人的自身利益不存在损害和泄露成为当前关注热点之一。2020 年发布《数据安全法（草案）》，明确规定任何组织、个人收集数据过程中必须采取合法正当手段。大数据时代，信息技术使社会生活的产品和服务逐渐变为数据形态，数据资源的应用和使用正在逐渐渗透到各个行业领域，各方对隐私保护和数据安全使用问题更加重视。2006 年Dwork［1］提出的差分隐私（Differential Privacy，DP）是一种新型的隐私保护机制，严格定义了数据隐私保护的强度，对于一个数据集增加或删除任何一条记录都不会影响到最后的查询效果。相较于现有的隐私模型，例如K-anonymity、L-diversity、T-closeness 模型，需要特殊的攻击假设和背景知识的方法，差分隐私因自身隐私强度和独特优势受到当前学术界研究者的广泛关注。

聚类分析是数据挖掘的主要任务之一，在银行、医药等多个领域被广泛地应用。聚类对无标签的数据进行若干簇或类别的划分，根据获得数据的分布情况进行频率统计或均值求解。作为数据挖掘中一种聚类方法，K-Prototypes 算法［2］结合了K-means［3］和K-modes［4］聚类算法的核心，同样是将数据点到聚类中心的距离划分为K个聚类，使许多混合型数据得到了广泛的应用。这些数据为挖掘有用的信息提供了巨大的便利，但是也存在对隐私的威胁，因为这些数据通常包含个人的敏感信息，例如：攻击者可以从医疗处方中推断病人患的是哪种疾病，或者可以从用户的轨迹数据推断用户在哪里生活或工作。因此在获取高质量数据分析的同时，保护用户的隐私成为迫切需要。在聚类中引入差分隐私技术逐渐成为了研究热点。研究者针对信任模糊的第三方收集者，在中心化差分隐私的基础上细化了对个人隐私的保护，提出了本地化差分隐私（Local Differential Privacy，LDP）［5］。在不暴露任何用户隐私的前提下，在聚类分析中引入本地差分隐私，这样既保证了用户的隐私又保障了聚类的可用性。

1 相关工作

本地差分隐私将对数据集的隐私处理过程从第三方服务器转移至用户个人，使得用户个人对数据能够独立处理和保护自己的敏感信息。本地差分隐私的研究方向目前集中于扰动机制的研究以及统计数据之后发布操作［6］，且已经运用到实际任务中，例如谷歌浏览器使用RAPPOR（Randomized Aggregatable Privacy-Preserving Ordinal Response）方法［7］对分类型数据进行频率估计。RAPPOR 采用随机响应技术［8］和Bloom Filter 技术保证了数据收集者无法窥探到用户个人信息，对数据起到了隐私保护。Nguyên等［9］提出了对离散型数据的扰动方法Harmony，他们将Harmony 运用到随机梯度下降中，对每次迭代的梯度进行扰动，并证明了在本地差分隐私下的小批量梯度下降优于随机梯度下降。基于聚类分析进行隐私保护的研究中，Blum等［10］提出了一种差分隐私K-means 算法，可以有效防止隐私泄露；但由于增加了噪声，使聚类结果的可用性降低。Ren等［11］提出了一种新的基于差分隐私的DPLK-means（Differential Privacy Laplace K-means）算法，它通过对原始数据集划分的每个子集执行差分隐私K-means 算法来改进初始中心点的选择，相较于文献［10］算法提高了聚类结果的可用性。之后，越来越多的研究改进了支持差分隐私的Kmeans 聚类算法［12-13］。Xia 等［14］提出了分布式场景下的第一个本地差分隐私下K-means 聚类算法，与中心化差分隐私下的K-means 算法有相似的聚类性能。彭春春等［15］提出了一种支持本地化差分隐私技术的K-modes 算法，很大程度上降低了第三方窃取用户信息的可能性。Lv 等［16］提出基于中心化差分隐私的混合数据，目的是将K-means 和K-modes 算法结合处理混合型的数据集，进行聚类分析。由于目前的数据不再是单一型的数值型或分类型，在实际应用中，大量的数据集都是包含混合型的属性；因此受到可信的第三方数据收集者的假设限制，本文提出了一个支持本地化差分隐私技术的隐私保护聚类方案LDPK-Prototypes（Local Differential Privacy K-Prototypes）。LDPK-Prototypes 使用随机响应机制来扰动用户数据，使用户进行数据的隐私处理，服务端则负责收集和恢复数据集进行聚类，达到隐私保护目的的同时保证了聚类可用性。如图1 所示，与中心化差分隐私相比，本地化差分隐私技术能对用户的敏感信息实现更彻底的保护。

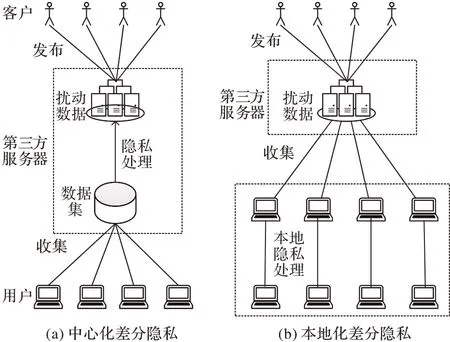
图1 数据隐私处理框架Fig.1 Data privacy processing framework

2 理论基础与定义

2.1 本地差分隐私

定义1LDP［5，17］。对于给定ε∈R+，给定n个用户，每个用户对应一条记录，随机扰动机制M，值域Range（M），当且仅当任意两条记录x、x'和输出结果y(y⊆Range(M)) 满足式（1），则M满足ε-本地化差分隐私。

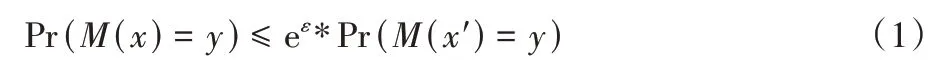
Range（M）表示经过随机扰动机制后产生的所有数据集合；ε（隐私预算）越小，对于数据隐私保护程度越强，同时数据的实用效果越弱。

差分隐私的组合性可以进行更优的隐私预算分配，达到更好的隐私保护效果；同样本地差分隐私也具有以下性质。

性质1 序列组合性［18］。假设给定数据集U，具有n个随机响应算法M，如Mi={M1，M2，…，Mn}，算法Mi满足εi-本地差分隐私，则n个Mi（U）算法构成的序列也满足本地差分隐私。

性质2 并行组合性［18］。假设给 定数据 集U={U1∪U2∪… ∪Un}，其中数据集Ui（1 ≤i≤n）和Uj（1 ≤j≤n，i≠j）是互不相交的子集，算法Mi满足εi-本地差分隐私，则n个Mi（Ui）算法构成的序列也满足max｛εi｝-本地差分隐私。

2.2 K-Prototypes聚类算法

设一个数据集U={X1，X2，…，Xn}，一共有n个数据记录，并且数据集中每个数据记录有d个特征，即Xi={xi1，xi2，…，xip，xi(p+1)，…，xid}（1 ≤i≤n），xi1～xip表示数值型特征共有p个，xi（p+1）～xid表示分类型特征共有q（q=d-p）个。首先设聚类的个数为K，最开始的簇中心集合为V={V1，V2，…，VK}，随着不断地重复迭代获得的中间过程簇中心集合为O={O1，O2，…，OK}，距离公式如定义2 所示。

定义2样本Xi到聚类中心样本Vi的距离为：

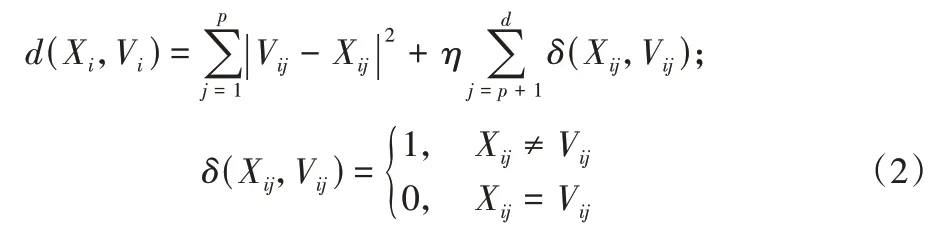
其中：η是分类特征的权重，用来调节两种不同类型数据对总体距离贡献度的比重，从而避免聚类结果值偏向分类型特征或者数值型特征。

定义3数据集U在聚类过程中划分类簇表示为集合O={O1，O2，…，OK}，其中K表示簇中心集的个数并且Oi∪Oj=∅（1≤i，j≤K），即集合O是数据集U的一个聚类划分，依此循环。

K-Prototypes 算法的目标函数如下所示：

其中：∂ij∈｛0，1｝，1 表示数据记录Xi被聚类划分至第j个类簇中心集；0 表示未划分，每个数据记录仅被划分到一个类簇中心集。

2.3 优化差分隐私聚类算法

Lv 等［16］提出了基于K-means 和K-modes 两种算法相结合的中心化差分隐私，称为ODPC（Optimizing and Differentially Private Clustering）算法，主要思想为：对于数值型的特征，采用拉普拉斯机制对中心加噪；对于分类型的特征，采用几何机制对属性的频率加噪。添加噪声的频率上选择质心对应的属性值。引入真实的质心和加噪后的质心之间的损失函数来计算分配每次迭代过程的最小隐私预算，并由总的隐私预算和最小的隐私预算来确定迭代次数。

算法1 ODPC 算法。

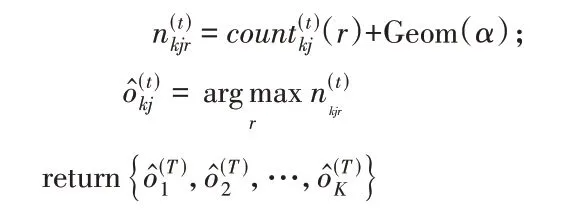
Lv 等［16］提出的ODPC 算法是建立在可信第三方服务器基础上进行数据的统计和共享，但可信的第三方服务器在实际应用中并不存在；由于初始聚类中心点是随机选取的，可能会导致算法陷入局部最优解，以及忽略了不同属性对聚类结果的影响程度，导致运行结果不稳定。针对上述问题，本文提出基于本地差分隐私的改进的K-prototypes 聚类算法，即LDPK-Prototypes。

3 LDPK-Prototypes聚类算法

3.1 聚类算法的改进

3.1.1 聚类中心的选取

基于K-Prototypes 聚类算法［19］的初始聚类中心是随机选择的，这种随机性会导致算法陷入局部最优，运行结果不稳定；因此结合文献［20］中给出的相异性度量方法对初始聚类中心的选取进行改进，扰动后的数据集U={X1，X2，…，Xn}，具体方法如下。

定义4用数据记录的欧氏距离表示它们之间的相异度：

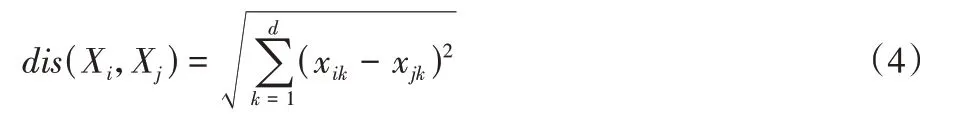
定义5构造相异矩阵，记为Qdis。

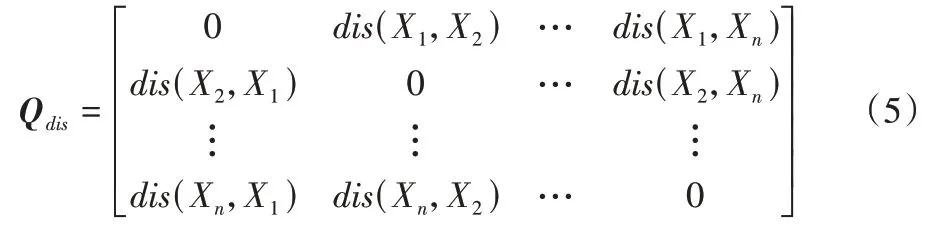
定义6均值相异性是数据点Xi与数据集中每个数据记录的距离平均值，记为Adis（Xi）。

其中：Adis（Xi）反映数据记录Xi在整个数据集的位置情况，其值越大，说明Xi周围数据分布越稀疏且与其他数据记录远离程度越高；反之越稠密。

定义7数据集的总体相异性定义如下：

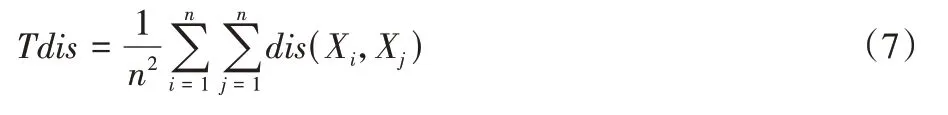
数据集的总体相异性与全体数据的分布有关，体现了数据集的稀疏程度。

算法2 聚类中心选取。

步骤1 对数据集的属性进行预处理，防止数值之间差异过大，影响距离计算。

步骤2 根据式（4）～（7），分别计算相异度dis、构造相异矩阵Qdis、均值相异度Adis（xi）和总体相异度Tdis。

步骤3 选取arg max［Adis（xi）］为第1 个初始聚类中心o1，接着从剩余的数据记录中选取arg max［Adis（xi）］，计算与之前的聚类中心的相异度：若dis(xi，oj|j=1，2，…，K-1) ＞Tdis，则聚类中心加1；否则选取第2 大的均值相异度进行计算，依次进行选取。

步骤4 若选取聚类中心个数满足要求，则聚类中心选取完毕，否则重复步骤3。

3.1.2 熵权法

K-prototypes 算法中数值型和分类型的权重η是人为地随机指定，这样对聚类的效果会造成影响；另外由于数值型特征和分类型特征的差异度计算存在缺陷，忽略了不同属性对于聚类结果的影响程度，没有全面地考虑两种类型数据的结构特点，造成分类型特征差异度权衡类内总体对象的差异度。基于上述问题，提出加入熵权法来衡量不同属性的权重，从而提高算法的准确率。具体步骤如下。

1）数据标准化且非负处理。

假设数据集共有k个属性，U={X1，X2，…，Xn}，其中Xi={xi1，xi2，…，xij}（1 ≤i≤n，1 ≤j≤k），因此对各数据集属性标准化后的值为yij，则：

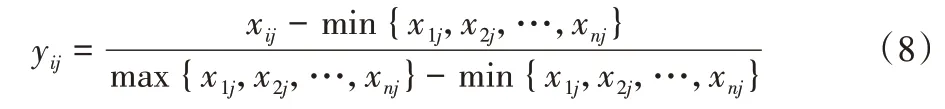
2）计算各个属性的信息熵：

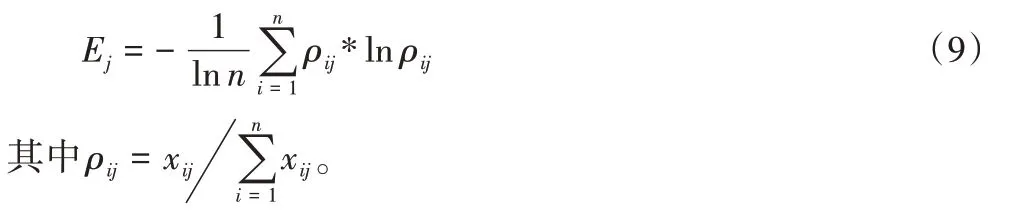
3）确定各属性的权重：

属性的差异性大小和聚类过程中属性的重要程度成正比，特征的熵值增大，则特征的差异性随之增大，导致特征赋予的权重比例越高；反之亦然。

3.1.3 改进的K-Prototypes算法

设一个数据集U={X1，X2，…，Xn}，共有n个数据记录，xi1～xip表示数值型特征共有p个，xi（p+1）～xid表示分类型特征共有q（q=d-p）个。

定义8样本Xi到聚类中心样本Vi的新距离为：

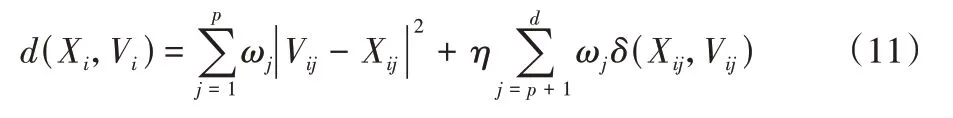
相较于其他的K-Prototypes 算法，本文算法的聚类中心不再随机选取，而是根据相异性度量的方法求解，避免了局部最优情况，提高了聚类算法的准确性和稳定性。考虑了不同属性之间的差异性，利用熵权法对各个属性进行权重赋值，有效避免了不同属性对聚类结果的影响。

算法3 改进的K-Prototypes 算法。

输入 类簇中心个数K，含有n个数据记录的混合型数据集U；

输出 划分结果K个簇C={C1，C2，…，CK}。

步骤1 根据算法2 计算得出K个类簇中心集V={V1，V2，…，VK}。

步骤2 由式（10）得出数据集的属性权重，将其代入新的距离公式（11）。

步骤3 然后根据式（11），计算剩余的n-K个数据记录与类簇中心之间的d（Xi，Vj），根据所得的结果向最近的类簇中心聚类划分。

步骤4 重新计算K个类簇集合的数值型和分类型簇中心。

步骤5 重复步骤3、4，直到K个簇类的簇中心不再变化，即损失函数E的结果值不再发生变化，将得到最终的聚类结果。

3.2 用户端-服务端概况

3.2.1 用户端操作

基于本地差分隐私的方法是对本地位置进行保护，用户需要执行编码和扰动两个步骤。假设数据集U={X1，X2，…，Xn}，一共有n个数据记录，xi1～xip表示数值型特征共有p个，xi（p+1）～xid表示分类型特征共有q个。

1）编码（Encode）。

①数值型特征。

对于Xi的p个数值型特征，需要将其转换成0/1 字符串。其中xip转换为Bip={b1，b2，…，bm}，m=|B|ip是字符串长度，具体如下：

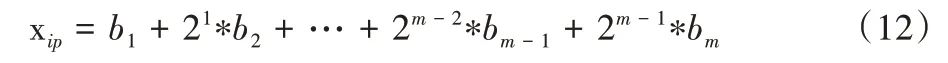
②分类型特征。

对于Xi的q个分类型特征，则首先利用LabelEncoder 标签编码进行转化，将特征值置为相应的序号xiq∈{1，2，…，k}，再按数值型特征方法进行转换。

2）扰动（Perturb）。

根据上述编码后的二进制字符串，利用随机响应机制［8］实现本地差分隐私的每位比特位的扰动，Bip扰动后表示为，具体扰动机制如下：

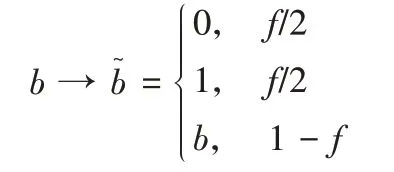
根据扰动机制可以看到每个比特位扰动为”1”或”0”的概率都是f/2，可以看出每位比特如何进行扰动，第三方收集者也无法知道确切真实值；因为用户告诉服务端的真实值可能性很小，即1 -f，显然f越大得到的隐私保护越强。经过这种扰动方式后每个比特位满足ε-本地差分隐私［7］，其隐私预算为ε=ln

算法4 特征扰动。

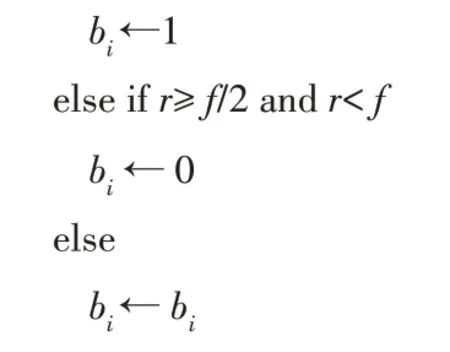
3.2.2 服务端操作

用户数据集U={X1，X2，…，Xn}，其中含有d维属性，表示数值型特征共有p个，分类型特征共有q(q=d-p)个。服务端目的在于根据用户上传数据信息后将用户划分为K个簇并返回最终的簇中心C={C1，C2，…，CK}及类簇集合；在用户将数据上传服务端时需提前进行扰动保护其自身隐私，服务端收集完之后要将扰动后的特征信息尽量恢复至原始的信息，具体做法指将扰动后的二进制数据转换为初始的整数，以便更好分析用户聚类效果。具体的操作流程如图2所示。

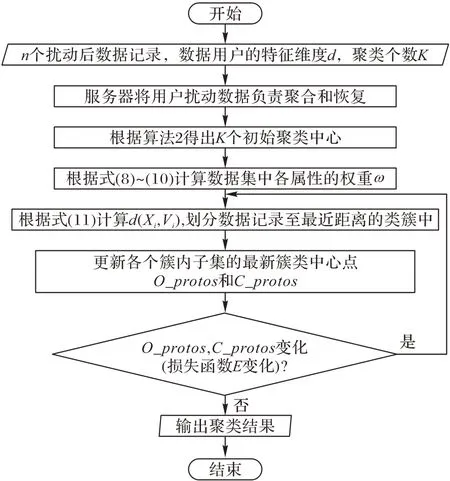
图2 LDPK-Prototypes流程Fig.2 Flow chart of LDPK-Prototypes

3.2.3 聚类方案

本文提出LDPK-prototypes 聚类方案如图3 所示。方案由用户端和不可信的第三方服务器组成。用户端负责用户数据的隐私处理，即扰动，相较于中心差分隐私，对于敏感数据的隐私处理在于用户，有效地保护了用户的个人隐私。服务器端则负责对扰动数据的收集和恢复及聚类。用户端采用3.2.1 节的方法将数值型和分类型的数据进行随机响应方式扰动处理，扰动结束后将数据上传至服务器端。不可信的服务器端则负责收集扰动数据进行数据的恢复和合成，最后在生成的数据集中选取适当的聚类中心，按3.2.2 节的算法流程执行K-prototypes 聚类算法，具体过程如算法2。

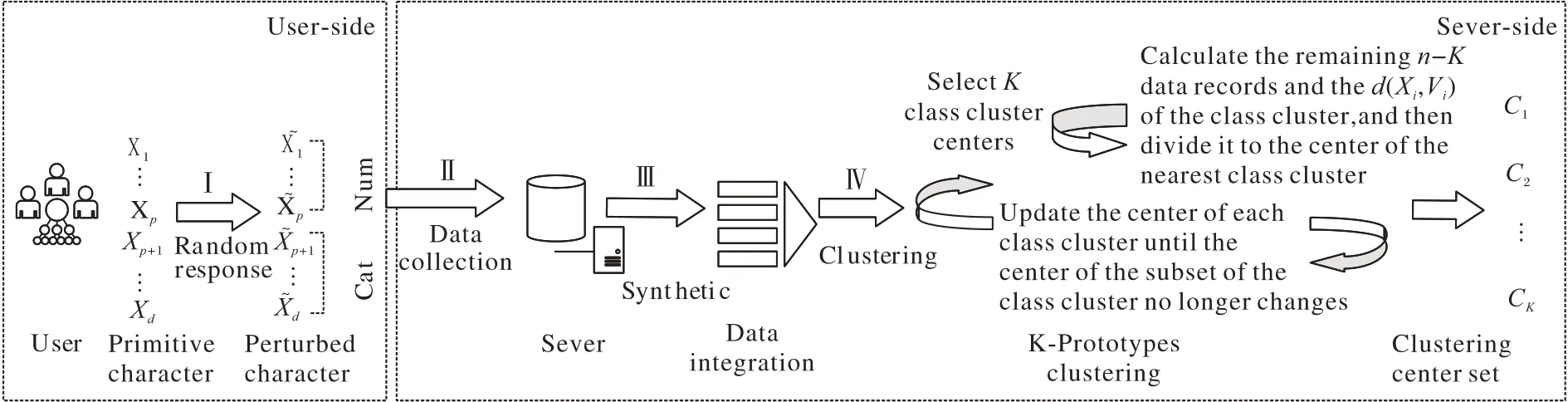
图3 LDPK-prototypes聚类方案Fig.3 LDPK-prototypes clustering scheme

3.3 隐私分析

本节将从本地差分隐私的定理以及部分性质对LDPKprototypes 算法的隐私进行分析证明。

定理1每位比特经过算法4 扰动后，每个比特位满足ε1-本地差分隐私，其中ε1=。

证明 根据用户端编码扰动过程：

定理2当每一位扰动后的比特位满足ε1-本地差分隐私，则每个用户扰动后的特征xid也满足mε1-本地差分隐私，同时每个用户记录Xi也满足本地差分隐私。

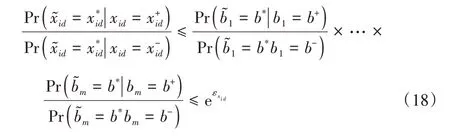
其中：

4 实验与结果分析

4.1 实验环境与数据集

本文实验的硬件环境为：Intel Core i5-7200U CPU 2.50 GHz 处理器，内存8 GB，操作系统为Windows 10 64 位，使用Python 语言进行仿真实验。实验的数据集采用UCI 数据集中的Adult 数据集和Heart 数据集，Adult 数据集有48 842个数据记录，是混合型数据集，考虑到空属性的影响，最终共有30 161 个数据记录，本文选择4 个数字属性和6 个分类属性构成数据记录；同样Heart 数据集共有918 个数据记录，选择4 个数值属性和4 个分类属性构成数据记录。不同数据集的特征如表1 所示。

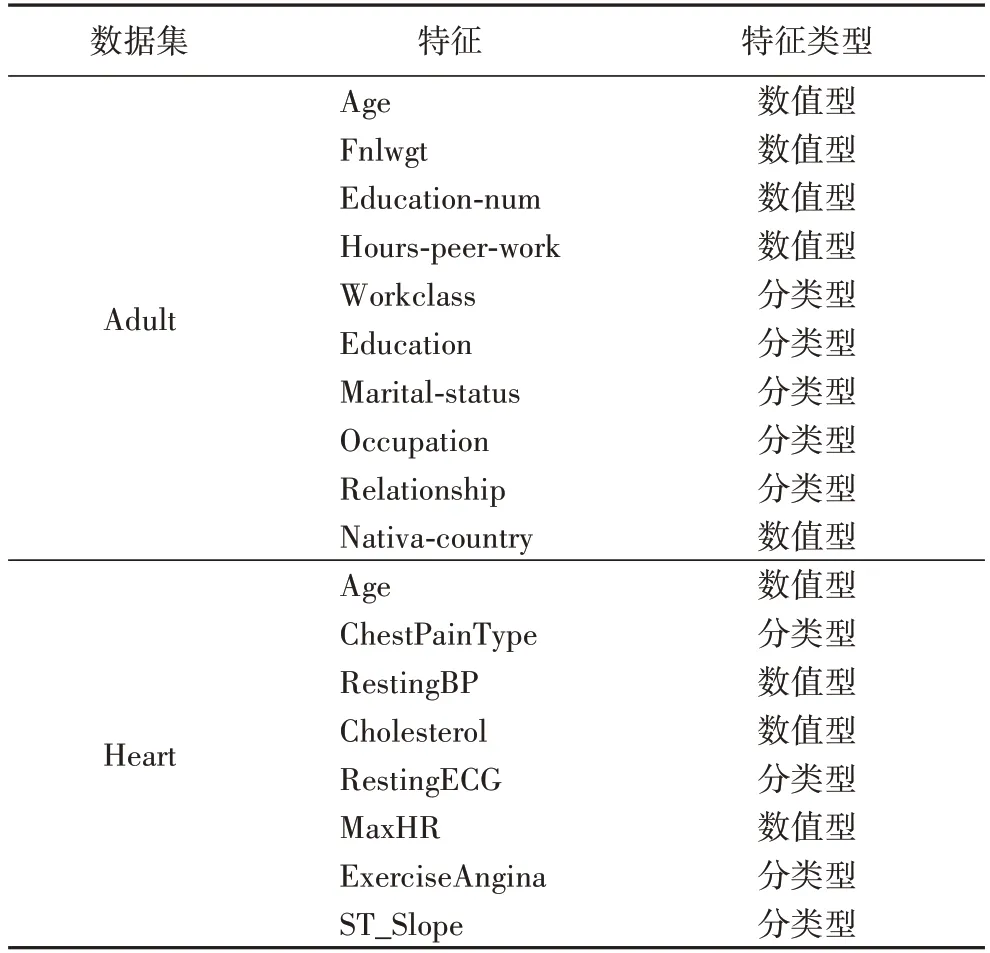
表1 不同数据集的特征Tab.1 Characteristics of different dataset

4.2 实验评价标准

由于噪声的引入，数据可用性的影响在隐私保护中尤为重要，通过采用F-measure 值（F）［21］可以很好地衡量加噪后的数据的可用性；与其他评价指标相比，F-measure 值得到的结果更有针对性。F-measure 值结合了数据挖掘与信息检索中准确率（ACcuracy，AC）和召回率（REcall，RE），定义如下：

为了使召回率和准确率获得同等的权重，设置α=1。F-measure 值的范围在［0，1］，如果得到F-measure 值越大则意味着聚类算法得到的结果可用性越高。

另外，采用规范化簇内方差（Normalized Intra-Cluster Variance，NICV）［22］可以很好地衡量聚类效果。计算公式如下：

其中：n为数据集的大小，Ci是第i个簇心，x为每个类簇的数据记录。NICV 值越大则聚类效果越差，反之说明聚类效果越好。

最后，采用兰德系数（Rand Index，RI），它是比较两个聚类结果差异性的指标，也可以比较一个聚类算法的结果和真实分类情况。本文用其衡量两个簇类的准确率，其公式为：

其中：是所有可能的样本对个数，a表示两个簇类中的同类别的元素对数，b表示两个簇类中的不同类别的元素对数。RI取值范围为［0，1］，值越大意味着两个簇的聚类结果越相似。

4.3 实验结果分析

实验分别在Adult 数据集和Heart 数据集上运行了未受任何隐私保护的聚类算法K-Prototypes 算法、EKPCA（Enhanced K-Prototypes mixed data Clustering Algorithm）［23］、ODPC 算法［16］以及本文提出的LDPK-Prototypes 算法。在数据集上运行50 次未进行隐私保护K-Prototypes 算法和EKPCA，取得聚类效果最好情况下的NICV 指标作为评估的参照物，设置隐私预算ε为｛0.01，0.1，0.2，0.5，1，1.5，2｝，在相同ε值下，在数据集上分别运行ODPC 算法和LDPKPrototypes 算法20 次后得到F-measure 和NICV 的平均值。

1）隐私预算ε对NICV 的影响。

如图4 所示，改进后的K-Prototypes 算法相较于EKPCA有着同等优势的聚类效果。由图4（b）可看出，改进的K-prototypes 算法相较于EKPCA 算法的聚类效果提高了28.61%。当隐私预算ε较小时，LDPK-Prototypes 算法比ODPC 算法有更好的聚类效果，随着隐私预算ε的增加，ODPC 算法的NICV 随着ε值的增大曲线变化较明显，而LDPK-Prototypes 算法则相对稳定降低；这是由于LDPKPrototypes 算法对聚类中心的优化选择及属性相异度增强了聚类的效果。

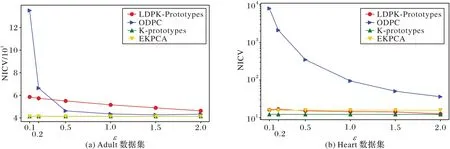
图4 不同数据集上不同ε下的NICV值比较Fig.4 Comparison of NICV value under different ε values on different datasets

2）隐私预算ε对F-measure 值的影响。

如图5 所示，当隐私预算ε较小时，ODPC 算法比LDPKPrototypes 算法的聚类可用性高；这是因为本文提出的算法是基于不可信的第三方数据处理，在隐私预算ε较小时，为了达到相似的隐私保护性需要加入更大的噪声保护初始数据。随着ε的增加，LDPK-Prototypes 算法的F也逐渐增加且高于ODPC 算法，因为隐私保护程度降低同时添加的噪声量也会降低，而本地差分隐私随着隐私预算的增加可以以更高的概率将原始数据的信息保留，较小的概率扰动为差别很大的数据信息，因此聚类可用性也得到提高。

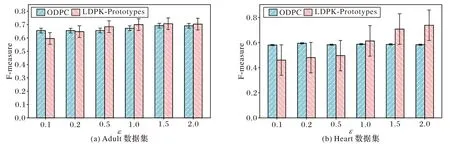
图5 不同数据集上不同ε值下F-measure值的比较Fig.5 Comparison of F-measure value under different ε values on different datasets

3）其他指标分析。

由图6 可以看出，随着ε值的增大LDPK-Prototypes 算法的RI 值均高于其他算法，这表明本地化差分隐私技术加噪后的聚类效果优于中心化差分隐私技术加噪后的聚类效果，主要原因是聚类中心点选取是根据数据记录的差异度来确定聚类个数，有效地避免了局部最优，提高了算法的稳定性。由表2 可见，在不同数据集上LDPK-Prototypes 算法比ODPC算法平均准确率分别提高了2.95%和12.41%。

表2 不同数据集上RI值的对比Tab.2 RI value comparison on different datasets

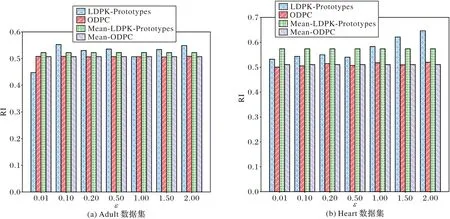
图6 不同数据集上RI值与均值对比Fig.6 RI value and mean value comparison on different datasets

最后，在整个聚类过程中，本文提出的 LDPK-Prototypes算法对于原始数据的处理只能通过用户自己，因此不需要担心第三方数据收集者是否可信；这样的隐私保护性较强，适用场景更广，实用程度更高。

5 结语

本文提出了一种基于改进的K-Prototypes 本地化差分隐私聚类方案。在聚类过程中，使用相异性度量方法确定初始聚类中心；利用熵权法重新定义距离计算公式，扩大了数据之间差异性，提高了算法的准确率和稳定性。在不需要可信第三方的前提下，本文算法与ODPC 算法有着相似的聚类性能表现。在未来研究中拟用混合不同的隐私方法处理数据集，用LDP 保护用户在其隐私要求级别内的数据隐私，用中心化差分隐私（Central Difference Privacy，CDP）保护用户隐私免受其他可能的对手的攻击。