基于格拉斯曼流形子空间融合的多视图聚类

管娇娇，钱雪忠，周世兵，姜凯彬，宋 威

（江南大学 人工智能与计算机学院，江苏 无锡 214122）

0 引言

在信息时代，数据呈指数级爆炸式增长，对模拟对象进行合理的分类，减小数据的混淆程度格外重要。目前，聚类被广泛应用于数据挖掘、计算机视觉、模式识别和人工智能领域。一些著名的单视图聚类算法如k-means算法、谱聚类算法发挥着越来越重要的作用；然而经过多年的发展，传统单视图聚类研究几乎达到了瓶颈，主要原因是从单个方面描述对象得到的数据不能准确掌握对象的全面信息，特别是观测不充分或数据严重受损的情况下。

多视图数据的大量出现意味着从不同的角度描述相同的对象，不同的视图可以提供互补信息。一个网页可以划分为两个视图，分别显示出现在给定页面上的单词和在超链接中的单词；同一个单词可以使用多种语言描述，图像可以使用形状、颜色、纹理等描述。多视图聚类假设所有视图共享相同的底层聚类结构，通过组合来自不同视图的信息，试图获得比简单特征串联更准确的聚类结果。现有的多视图聚类算法可以分为以下几种：基于协同训练的多视图聚类算法、基于多核学习的多视图聚类算法、基于子空间的多视图聚类算法。

基于协同训练的多视图聚类算法旨在通过交替训练来最大化不同视图之间的一致性，代表算法有：Co-reg（Coregularized multi-view spectral clustering）［1］假设每个样本在所有视图中共享同一个聚类结果，将不同视图之间的拉普拉斯算子的特征向量最小化；Co-train（Co-training approach for multi-view spectral clustering）［2］假设最优聚类会将同一个样本的所有视图划分到同一个聚类中，利用其他视图返回的聚类信息对图结构进行交替修改。

基于多核学习的多视图聚类算法把每个核看作一个视图，将这些核进行线性或非线性组合，以此提高聚类性能，代表算法有：SMSCK（Smoothness regularized Multiview Subspace Clustering with Kernel learning）［3］将多视图数据点映射到高维核空间中，并引入平滑正则化项来提高聚类性能；一步核多视图子空间聚类（One-step Kernel Multi-view Subspace Clustering，OKMSC）［4］将亲和矩阵的非负性和判别性融合到计算过程中。

多视图子空间聚类算法是由单视图子空间聚类算法发展而来的，单视图子空间聚类的代表性算法有：SSC（Sparse Subspace Clustering）［5］、LRR（Robust Recovery of subspace structures by Low-rank representation）［6］、LRSSC（Low-Rank Sparse Subspace Clustering）［7］等 。MVSC（Multi-View Subspace Clustering）［8］对每个视图的子空间表示同时进行聚类并保证了不同视图之间的一致性。MLRSSC（Multi-view Low-Rank Sparse Subspace Clustering）［9］利用低秩正则化和稀疏正则化，从每个视图的子空间表示学习一个共有表示矩阵，一步构造亲和矩阵。LMSC（Latent Multi-view Subspace Clustering）［10］通过挖掘多视图数据的潜在表示，获得了良好的聚类性能。DiMSC（Diversity-induced Multi-view Subspace Clustering）［11］利用希尔伯特施密特独立准则来探索多视图数据的底层聚类结构。ECMSC（Exclusivity-Consistency regularized Multi-view Subspace Clustering）［12］引入一个新的位置感知排他项，利用不同视图之间的互补信息实现聚类。DALIGA（Direct Affinity Learning via Integrative Grassmann Alignment）［13］保留了视图的几何结构，取得了较好的性能。LT-MSC（Low-rank Tensor constrained Multiview Subspace Clustering）［14］将不同视图的子空间表示矩阵视为一个张量，使用低秩张量约束来捕获多视图数据的高阶相关性。GLTA（Graph regularized Low-rank representation Tensor and Affinity matrix）［15］采用奇异值分解的张量核范数来探索高阶相关性。GNLTA（Generalized Nonconvex Low-rank Tensor Approximation for multi-view subspace clustering）［16］采用低秩张量近似来捕获多视图之间的高阶相关性，提出广义非凸低秩张量范数。WTSNM（Weighted Tensor Schatten p-Norm Mininization）［17］提出加权增强张量核范数。基于低秩矩阵分解的秩一致性诱导多视图子空间聚类RC-MSC（Rank Consistency induced Multiview Subspace Clustering via low-rank matrix factorization）［18］追求视图特定自表示系数矩阵之间的一致低秩结构。MSCBDR（cauchy loss induced Block Diagonal Representation for robust Multi-view Subspace Clustering）［19］对嵌入在多视图数据中的噪声和离群值提供优越的鲁棒性。

然而，现有的方法大多在以下方面还存在不足：1）现有方法旨在解决线性子空间的聚类问题，但大多数真实世界的数据集可能表现出非线性；2）在原始特征空间中相近的两个数据点在对应的表示空间中不一定相近，这破坏了表示矩阵的几何特性，影响聚类性能；3）来自不同视图的数据通常具有不同的结构，直接在欧氏空间中融合得到一致性亲和矩阵过于单调，无法对学习到的子空间进行对齐。因此，本文提出了基于格拉斯曼流形融合子空间的多视图聚类算法。该算法利用局部流形结构和内核技巧来学习每个视图对应的子空间表示，然后将每个视图的子空间表示矩阵在格拉斯曼流形上对齐，得到一致性亲和矩阵，并通过谱聚类得到最终的聚类结果。

本文的主要工作有：1）提出基于格拉斯曼流形融合子空间的多视图聚类算法；2）利用交替方向乘子法（Alternating Direction Method of Multipliers，ADMM）优化本文模型。该模型有3 个优点：一是将原始特征空间的数据点映射到高维核空间，并保留了局部流形结构；二是对每个视图学习到的子空间表示在格拉斯曼流形上对齐，得到一致性亲和矩阵，保证了几何一致性；三是对一致性亲和矩阵施加秩约束，使一致性亲和矩阵的连通分量等于聚类的个数。与核多视图低秩稀疏子空间聚类（KMLRSSC）算法相比，所提算法的聚类精度在MSRCV1、Prokaryotic、Not-Hill 数据集上分别提高了20.83 个百分点、9.47 个百分点和7.33 个百分点。

1 相关工作

1.1 符号与定义

在本文中，标量用小写字母表示，向量用粗体小写字母表示，矩阵用粗体大写字母表示。表1 中列出了常用符号及其定义，其中矩阵的Frobenius 范数的符号定义为：‖· ‖F，矩阵的迹定义为tr (·)，矩阵的秩定义为rank (·)。

表1 常用符号及其定义Tab.1 Common symbols and their definitions

1.2 核学习

根据自表示性质，每一个数据点都可以被表示为其他数据点的线性组合。这种线性组合表明了样本之间的相似性，自表示矩阵可以通过求解式（1）得到：

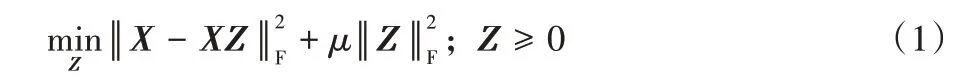
但实际生活中，数据点之间的非线性关系广泛存在，根据文献［3］，内核技巧可将原始数据空间中的非线性数据映射到高维核空间中，将输入空间的非线性问题转换成特征空间的线性分析问题。在式（1）的基础上使用内核技巧，得到：

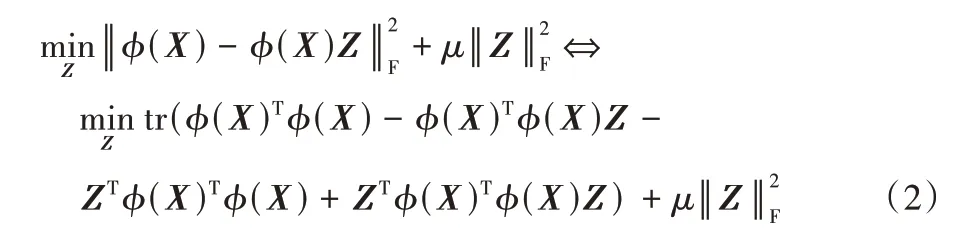
ϕ(X)是一个非线性特征映射，可以将数据映射到希尔伯特空间。假设核Gram 矩阵K=ϕ(X)Tϕ(X)，则式（2）可表示为：

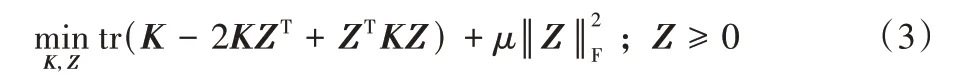
1.3 局部流形结构

假设xi和xj是特征空间的数据点，zi和zj是xi和xj对应的表示。根据文献［20］，在特征空间中相近的两个点在表示空间中也应有相近的表示，设S∈Rn×n为测量数据点之间的相似度，则有：

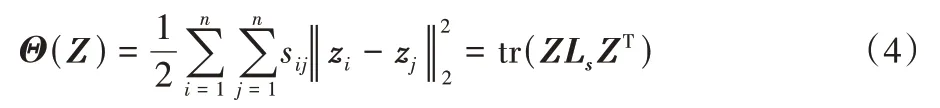
其中：Ls=D-S是拉普拉斯矩阵，D是度矩阵。当Θ(Z)最小化时，sij越小将会导致zi和zj的表示越近。由式（4）可知，学习到的表示矩阵符合原始特征空间的相似关系。

1.4 格拉斯曼流形融合子空间

格拉斯曼流形［13］被定义为n维欧氏空间的g维线性空间的集合。格拉斯曼流形结构的元素可以用一个标准正交矩阵U∈Rn×g来表示，其列可以张成对应的g维线性子空间span(U)。两个子空间的距离被定义为连接格拉斯曼流形的最短测地线的距离。两个g维线性子空间span(U1) 和span(U2)之间的投影距离为：

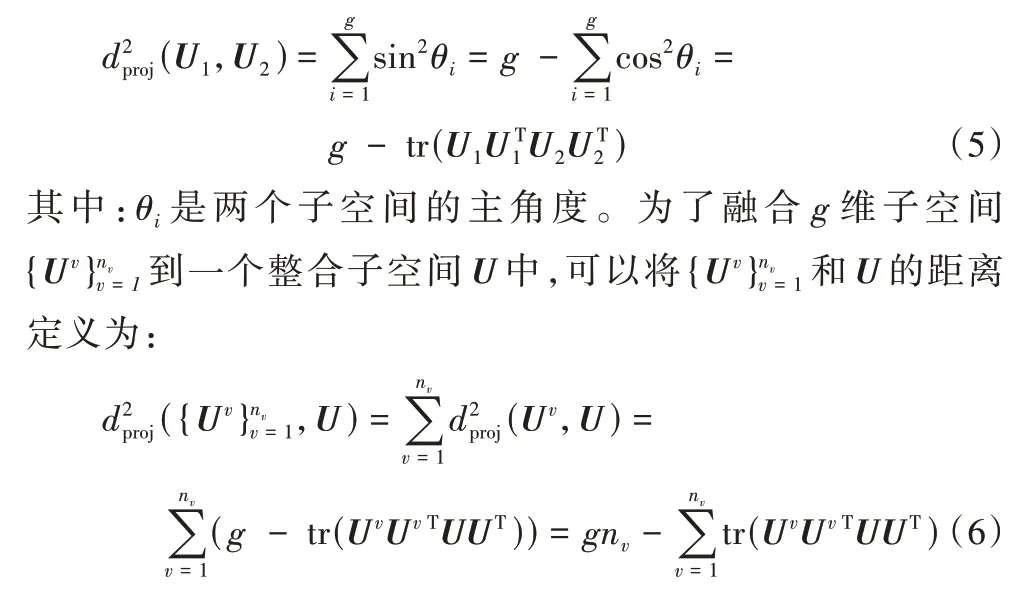
2 基于格拉斯曼流形融合子空间的多视图聚类

本章详细讲述基于格拉斯曼流形融合子空间的多视图聚类算法的模型，该模型首先将核学习和局部流形学习相结合，将原始特征空间的数据点映射到高维核空间，并保证原始特征空间相近的点在表示空间中也相近；然后基于格拉斯曼流形将学习到的子空间表示融合得到一致性亲和矩阵，并约束一致性亲和矩阵有k个连通分量，保证几何特性。

2.1 目标函数

对于单一视图Xv，通过核学习得到视图的子空间表示矩阵Zv(v=1，2，…，nv)，在式（3）的基础上加入局部流形结构的学习，推广到多视图子空间有：

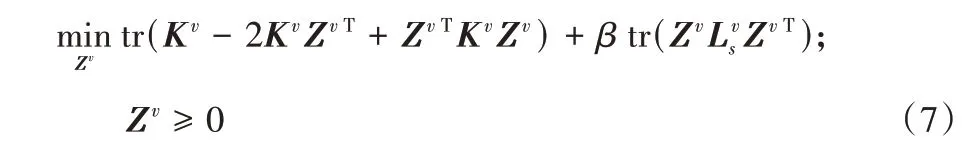
每个学习到的子空间表示Zv(v=1，2，…，nv)都是线性的，因此可以由一组基Uv张成。希望集成子空间到每一个子空间的测地线距离都最小化，即通过在格拉斯曼流形上将基向量对齐。集成子空间也是线性的，可以由一个基矩阵U张成。因此，在集成子空间中的样本亲和度由W=UUT给出。忽略常数项，可以得到：

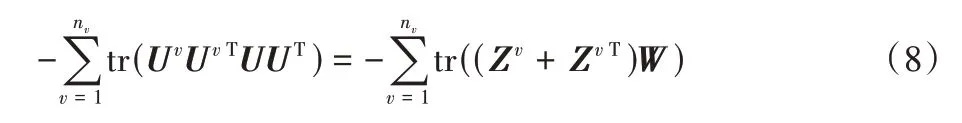
与欧氏距离中常用的相似性度量方法相比，格拉斯曼流形上的投影距离度量子空间之间的关系具有稳定性和鲁棒性。结合式（8），提出基于格拉斯曼流形融合子空间的多视图聚类算法，目标函数如下：

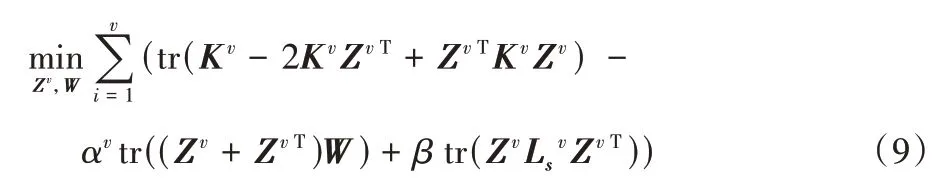
其中：αv是子空间表示学习和亲和矩阵学习之间的平衡参数，β是局部流形结构学习的平衡参数。此外，希望一致性亲和矩阵W应该有精确的k个连通分量，即数据点可以直接划分到k个聚类中，利用文献［21］中的定理实现。

定理1拉普拉斯矩阵L的零特征值的重数k等于相似图矩阵S的连通分量的个数。

由定理1 可知，如果满足约束rank (Lw)=n-k，则亲和矩阵W恰好有k个连通分量。则式（9）的模型可重新表示为：

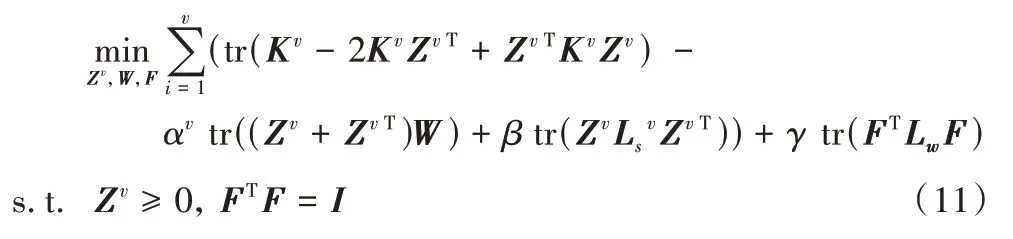
2.2 优化过程

2.2.1 固定W、F，求解Zv

式（11）去除无关项，则对于单一视图Zv有：

更新B1给定B2和Y2，将式（20）中的目标函数最小化得到B1的更新规则如下：

更新Y2给定B1和B2，则Y2的更新规则如下：

2.2.3 固定Zv、W，求解F

固定Zv、W时，认为式（11）的前三项为常数，则优化式（11）等价于优化：

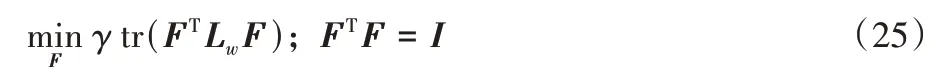
通过计算Lw的前k个最小特征值对应的特征向量，可以得到最优解F。

2.2.4 实现细节

在对Zv子问题和W子问题的进行交替方向最小化时，为了解决式（15）和（21）中的交互部分的问题，将式（15）中的更新修改为：

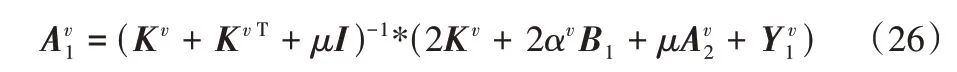
将式（21）中的更新修改为：

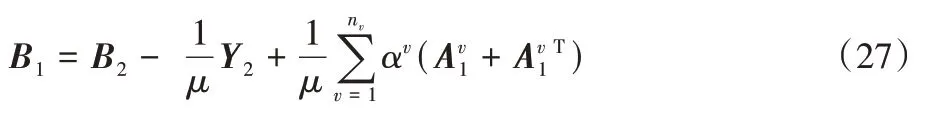
2.3 格拉斯曼流形融合子空间的多视图聚类

基于格拉斯曼流形融合子空间的多视图聚类算法如下。

算法1 基于格拉斯曼流形融合子空间的多视图聚类算法。

3 实验与结果分析

3.1 实验设置

3.1.1 对比算法

将本文算法与单视图聚类算法和多视图聚类算法进行比较，对比算法包括以下几种。

1）单视图算法：SC（Subspace Clustering）［23］对每个视图执行谱聚类算法，报告最优结果作为实验结果。

2）多视图算法：Co-reg［1］、Co-train［2］、MLRSSC［9］、KMLRSSC（Kernel Multi-view Low-Rank Spare Subspace Clustering）［9］、MLAN（Multi-view Learning with Adaptive Neighbors）［24］、LMSC［10］、DiMSC［11］、ECMSC［12］和DALIGA［13］。

3.1.2 数据集概述

本文在6 个公开数据集上进行了实验，分别是：MSRCV1数据集、Yale 数据集、Prokaryotic 数据集［9］、HW2sources 数据集、Not-Hill 数据集［25］和WebKB 数据集。#dv表示第v个视图的维数，具体情况如表2 所示。

表2 实验数据集Tab.2 Experimental datasets

1）MSRCV1 数据集。该数据集选取了树、建筑、飞机、牛、人脸、汽车和自行车的7 类图像共210 个样本，提取6 种图像特征组成视图，详见http：//research.microsoft.com/en-us/projects/objectclassrecognition。

2）Yale 数据集：该数据集包含165 张GIF 格式的15 个人的灰度图像。每个人有11 张图片，每张图片对应不同的面部表情或配置：中光、戴眼镜、开心、左光、不戴眼镜、正常、右光、悲伤、困倦、惊讶和眨眼，提取3 种图像特征作为视图，详见http：//cvc.yale.edu/projects/yalefaces/yalefaces.html。

3）Prokaryotic 数据集。该数据集中有3 个视图，每个视图包含551 种原核生物种类。此数据集和其他数据集的区别在于不同的聚类中物种的数量有很大不同，即33 个物种在一个大的簇中，35 个物种在一个小的簇中。

4）HW2sources 数据集。手写数字数据集（HW_2）包含2 000 个样本，实验中的两个视图来自于MNIST 手写数据集（0～9）和USPS 手写数据集（0～9），详见https：//cs.nyu.edu/～roweis/data.html。

5）Not-Hill 数据集。该数据集包含4 660 张面部图像，这里选择5 个类别的面部图像，每个类别抽取110 张人脸图像组成3 个视图用于实验。

6）WebKB 数据集。该数据集由4 个类别的203 个网页组成。每个网页都由页面的内容、超链接的锚文件和标题中的文本来组成3 个视图。

3.1.3 算法参数

对比算法的参数设置如表3 所示，其中SC、Co-train 和MLAN 算法没有参数。由于没有视图重要性的先验信息，因此假设α=αv。在核学习中，使用高斯核K(x，y)=，其中h在对｛0.5，1，5，10，50｝中搜索，其他参数保持不变。设置最大迭代次数为100，并报告最佳结果。

表3 对比算法参数设置Tab.3 Parameters setting of algorithms to be compared

3.1.4 评价指标

根据文献［26］，利用标准化交互信息（Normalized Mutual Information，NMI）、精度（Accuracy，ACC）、兰德调整系数（Adjusted Rand Index，ARI）、F-score、Precision 和Recall六个指标来评价聚类性能，每一个指标都度量聚类的特定属性，对于这些指标，值越高表示性能越好。

由于谱聚类算法都是基于k-means 算法的，不同初始化可能产生不同的结果，因此对实验运行20 次，并报告平均值和标准差。表4 给出了不同算法在6 个公开数据集上的聚类结果。在大多数情况下，本文算法都取得了较好的性能。

3.2 实验结果及分析

3.2.1 与经典算法进行比较

1）在大多数的情况下，本文算法优于对比算法或足以与对比算法相媲美，特别是在MSRCV1 数据集、HW2sources 数据集和Prokaryotic 数据集上的实验效果。在MSRCV1 数据集上，本文算法相较于次优算法分别提高了6.47（NMI）、7.62（ACC）、8.53（ARI）、7.25（F-score）、8.69（Recall）、5.62（Precision）个百分点。在HW2sources 数据集上，本文算法相较于次优算法分别提高了3.41（NMI）、7.86（ACC）、8.09（ARI）、7.24（F-score）、9.97（Recall）、4.14（Precision）个百分点。在Prokaryotic 数据集上，本文算法相较于次优算法分别提高了7.14（NMI）、9.13（ACC）、11.08（ARI）、7.90（F-score）、7.13（Precision）个百分点，仅在Recall 指标上低于MLAN 算法。

2）在Prokaryotic数据集上，基于单视图的谱聚类算法优于大多数多视图方法，这一结果可能是因为噪声或异常值引起视图多样性，多视图聚类受到较差视图的影响导致结果不佳。在其余5个数据集上，大多数多视图算法优于单视图算法。

3）对比多视图子空间算法，DiMSC 和ECMSC 在WebKB和Prokaryotic 数据集上效果不佳，可能是因为DiMSC 旨在从不同的视图中学习互补信息，如果视图之间存在较大的不一致，则DiMSC 可能得出不正确的结果；ECMSC 算法效果较差可能是因为两个数据集的多视图特征来自于多个来源，而不是像Yale 数据集中多视图特征是人工从同一对象中提取的。MLRSSC、KMLRSSC、DALIGA 算法采用低秩稀疏正则化，但均忽略了数据的局部流形结构，可能会获得较差的性能。

4）在表4 中，WebKB 数据集由大学计算机科学系收集的网页组成，包含203 个网页，分为4 个类别。每个网页由页面的内容、超链接的锚文本和标题中的文本组成。N/A 表示WebKB 数据集不适用于LMSC 和ECMSC 算法，得不到有效的聚类结果。

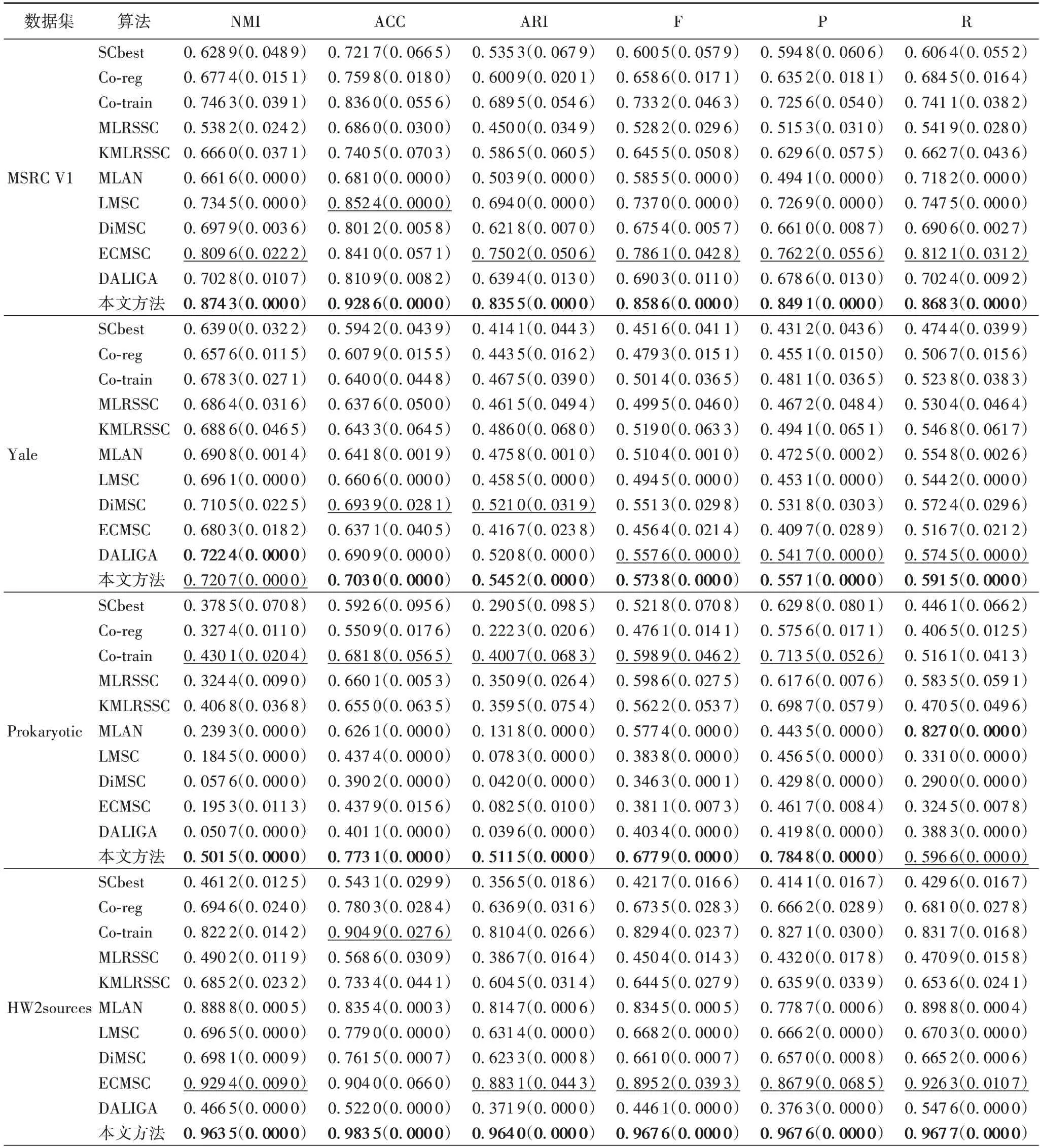
表4 MSRCV1、Yale、Prokaryotic、HW2sources、Not-Hill、WebKB数据集上不同算法的聚类表现Tab.4 Clustering performance on MSRCV1，Yale，Prokaryotic，HW2sources，Not-Hill，WebKB datasets among different algorithms

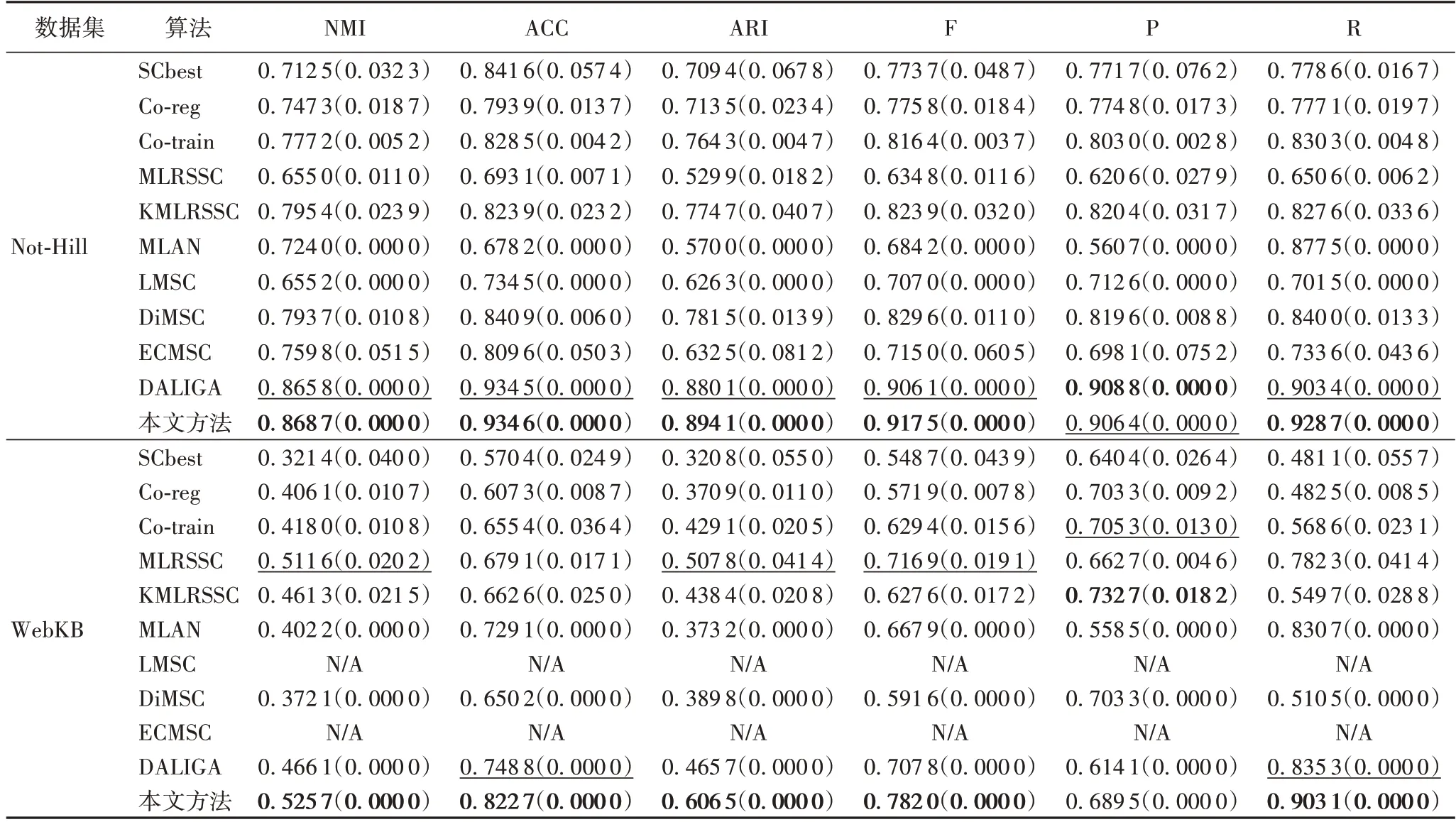
续表

3.2.2 收敛性和计算复杂度

根据文献［27］，交替方向乘子法的全局收敛性在理论上保证了式（11）中的线性约束凸优化问题。本文算法的时间复杂度为Ο(nvTn3)，其中：nv是视图个数，T是迭代次数，n是样本个数。

为了更直观显示本文算法的收敛性，式（11）中目标函数的值随着迭代次数的变化如图1 所示。在经过20 次迭代后，本文算法的目标函数值达到稳定状态。相较于对比算法，以MSRCV1 数据集为例，MLRSSC 算法在第76 次时达到收敛，LMSC 在129 次迭代时收敛，其余算法迭代次数均在10～30，很明显，本文算法收敛效率比较高，这也进一步表明了基于格拉斯曼流形融合子空间的多视图聚类的有效性。

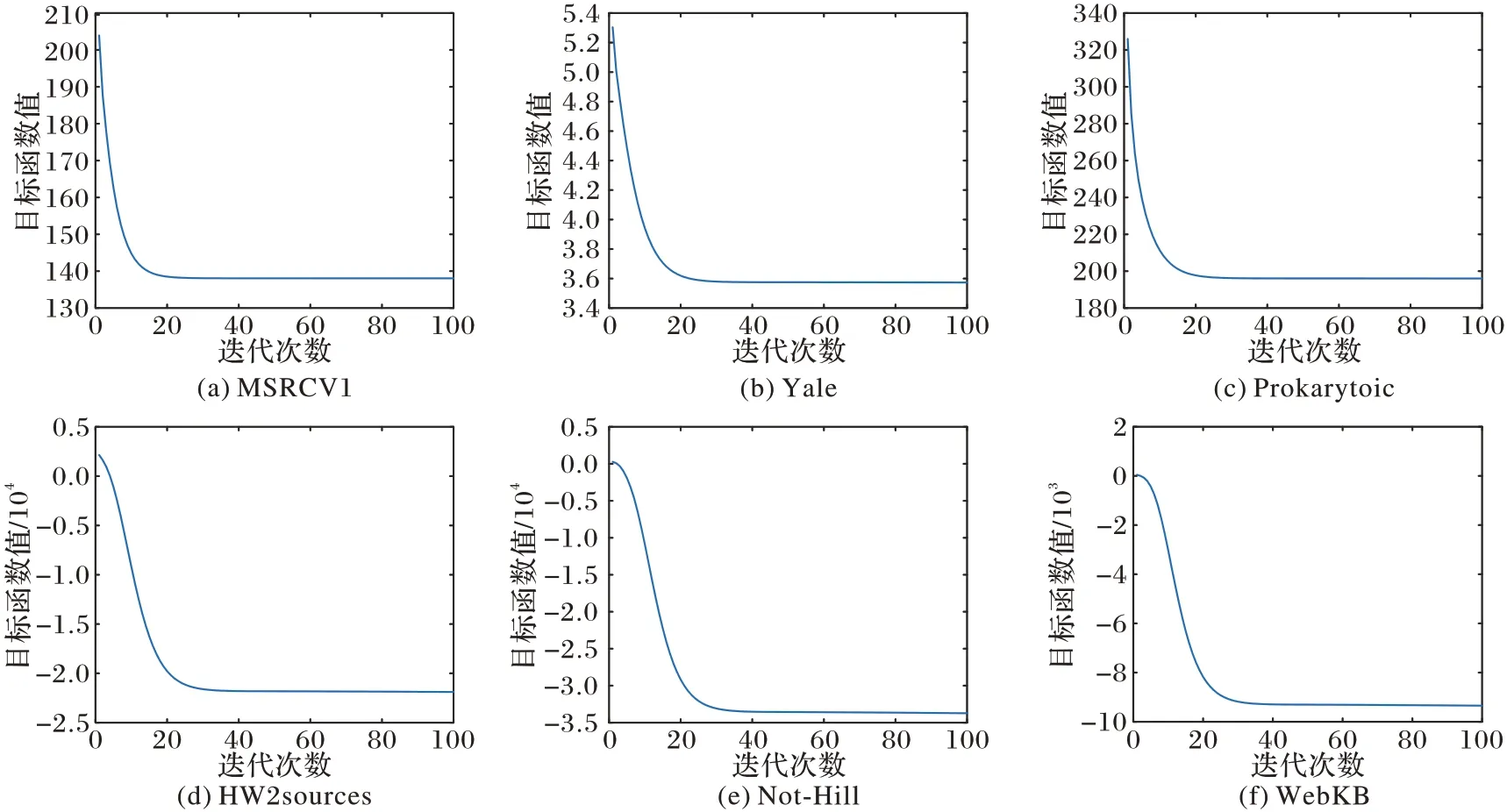
图1 本文算法在6个数据集上的收敛曲线Fig.1 Convergence curves on 6 datasets of the proposed algorithm

3.2.3 参数敏感性分析

图2为本文算法在MSRCV1、Yale、Prokaryotic数据集上的ACC值，因篇幅有限，未画出其余数据集的参数分析图。本文算法总共有α、β和γ这3个平衡参数需要调整。3个参数均从｛1E-7，1E-6，1E-5，…，1E-1，1｝中选取。根据文献［28］，首先，固定参数α和β，采用不同的γ值来观察γ对聚类指标ACC的影响。从图2第一行可知，当γ＞1E-3时，ACC显著下降。这是因为γ太大，一致性项可能会破坏每个视图的多样性；说明合适的γ取值可以让一致性项发挥更好的作用，促进一致性亲和矩阵的连通分量等于聚类个数。图2第二行显示了在固定γ（这里选取γ=0.001）时，不同的α和β的ACC值。结果表明，本文算法对α和β敏感，不同的数据集需要不同的参数组合才能达到最佳性能。合适的α和β可以使原始特征空间的相近的点在子空间中也相近，同时促进子空间表示在格拉斯曼流形上进行对齐。实际应用中，由于γ对聚类性能不敏感，所以可以先确定γ的取值，再通过交叉验证找到最优的α和β。

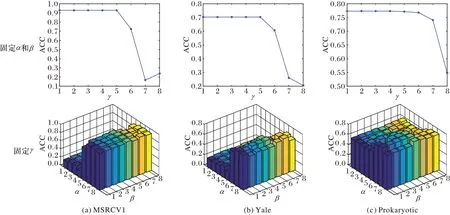
图2 本文算法在MSRCV1、Yale、Prokaryotic数据集上的参数敏感性Fig.2 Sensitivity of parameters on MSRCV1、Yale、Prokaryotic datasets of the proposed algorithm

在本文算法的实验中，MSRCV1 数据集最优参数的取值为｛0.01，0.001，0.001｝，Yale 数据集最优参数的取值为｛0.1，0.001，0.001｝，Prokaryotic 数据集最优参数的取值为｛0.1，0.001，0.001｝，WebKB 数据集最优参数的取值为｛1，0.01，0.1｝，HW2sources 数据集 最优参 数的取值为｛1，0.001，0.001｝，Not-Hill 数据集最优参数的取值为｛1，0.001，0.001｝。

3.2.4 t-SNE可视化

本节使 用 t-SNE（t-distributed Stochastic Neighbor Embedding）可视化直观比较本文算法得到的一致性亲和矩阵和LMSC 算法得到的一致性潜在表示。LMSC算法既不能捕获多视图数据点之间的非线性关系，在学习潜在表示时也不能保留原始特征空间的局部性，所以选择该算法做可视化的对比实验。使用t-SNE将LMSC算法获得的潜在表示和本文算法获得的一致性亲和矩阵映射到一个2D空间，并绘制成图。由于篇幅限制，仅给出MSRCV1、Prokaryotic 和HW2sources 数据集的t-SNE图。从图3可以看出，本文算法相较于LMSC算法更好地揭示了聚类的底层结构，即本文算法得到的聚类边界比LMSC算法得到的聚类边界清晰。可视化的结果进一步证明了捕获非线性关系和保留局部结构的重要性。

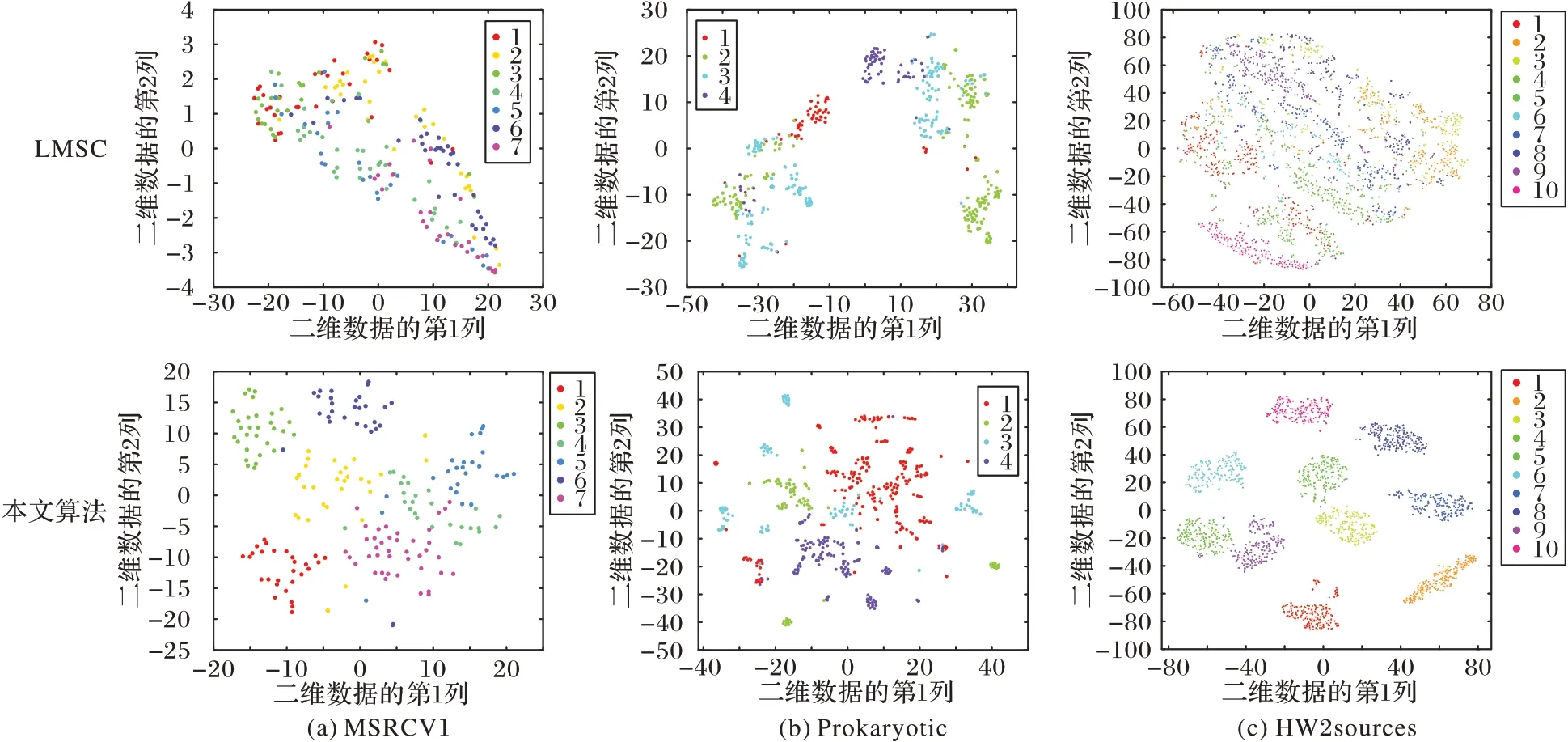
图3 本文算法与LMSC算法在MSRCV1、Prokaryotic、HW2sources数据集上的可视化Fig.3 Visualization on MSRCV1、Prokaryotic、HW2sources datasets of the proposed algorithm and LMSC algorithm

4 结语

本文提出了一种新的多视图子空间聚类算法，将核学习和局部流形学习相结合，得到每个视图的子空间表示矩阵，保证了原始特征空间中相近的数据点在子空间中也相近；然后将这些子空间表示矩阵在格拉斯曼流形上对齐，得到一致性亲和矩阵，并对一致性亲和矩阵施加秩约束，使一致性亲和矩阵的连通分量数等于聚类个数，从而提高聚类性能。本文提出的算法在6 个公开数据集上均取得了较好的效果，相较于其他9 种聚类算法，本文算法在6 个聚类指标上取得了更优的聚类结果。实验结果验证了基于格拉斯曼流形融合子空间的多视图聚类算法的有效性和良好性能。

本文算法虽然具有较好的聚类性能，但还有以下几个问题有待解决：

1）本文算法的时间复杂度很大程度上取决于样本的大小。在未来的研究中，可以利用基于锚图［29］的策略来提高本文算法的可扩展性。

2）根据文献［30］，在网页聚类和疾病诊断等实际应用中，不同视图的样本可能会缺失；如何将本文算法扩展到不完整多视图聚类将成为未来的一项重要工作。

3）基于低秩张量表示的多视图学习被广泛研究，例如文献［17］，如何在本文算法的基础上加入张量核范数来探索高阶相关性，从而进一步提高算法效率也值得深入探索。