基于时间序列的校园共享单车投放研究

许 可 胡日昊 李玮晔 黄素珍 刘桂兰

（盐城工学院，江苏盐城 224051）

共享经济[1]的不断发展，改变了人们的生活方式，共享单车的出现为人们的出行提供了极大的便利。大学校园里的共享单车的特点是单车的停放和使用都只能在校园内部，不可以将其骑行出校外并停放在校外。学生可以骑着共享单车穿梭在教室、宿舍、食堂和图书馆之间。但是不同地点所停放单车的数量，有时并不能够满足学生的需求。解决这一问题最直接的方法就是在学生常去和常在的地方大量投放单车，但过多投放会造成有些停车点单车闲置。科学预测每个停车点的单车投放量可以为制定合理的单车投放策略提供依据。

本文以盐城工学院希望大道校区为例，采集了不同时刻不同停车点的单车停放数据，基于时间序列分析方法，利用ARIMA算法和AR算法，对每个停车点的投放数目进行预测。以预测数目为依据，考虑损坏率，制定未来一周校园内各个停车点的投放策略。

1 数据调查

为了充分体现大学生日常出行的特点，本文借助手机软件“哈啰出行”获取盐城工学院希望大道校区八周内几个关键时刻，主要不同停车地点处的停放数目，如图1所示。

图1 “哈啰单车”单车停放数目界面

采集的数据包含四种属性：停车地点、停车数目、时间段、星期数。学生常去的地方主要有教室、宿舍、食堂、图书馆、操场等。因此，选取：一期宿舍群、二期宿舍群、博学楼、一期食堂、二期食堂、图书馆、操场、东大门、北大门以及两大二级学院楼群，共11个主要停放点。不同时间段学生使用单车量不同，一般上课前10 min和下课后10 min是单车使用的高峰期。因此选取：7：40、8：00、9：40、10：00、11：40、12：00、13：40、14：00、15：40、16：00、17：40、18：00、19：00、20：00共14个时刻。

设Xi(k)为停放数目，其中变量i表示停车地点的代号，共计11个，即i=1，2，…，11；变量k表示时刻标号，选取了共计14个典型的时刻，即k=1，2，…，14。其中地点名称对应的ID 如表1所示。

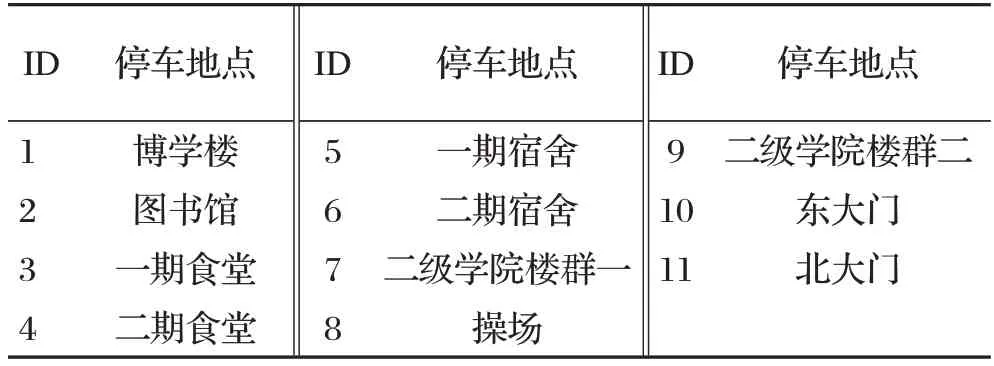
表1 停车地点名称及其ID

2 时间序列的判断与选择

由于大学生使用共享单车的频率既存在规律性，也存在着无规律性，所以搜集到的共享单车数据主要为白噪声序列与非平稳序列两种。例如周末为假期，老师和学生的活动并不确定，所以周末共享单车的使用就是一个白噪声序列，存在随机性，是无法使用时间序列来预测的；又如线下上课改为线上上课，也会大幅影响共享单车的使用。因此做如下假设：

（1）假设学生使用完共享单车后，都停放在常用停车点；（2）假设校园内共享单车不因损坏等因素而数目变少；（3）假设每天上课出行的学生人数不变；（4）假设周末学生不使用共享单车；（5）假设学生不将单车停放校门口外的“灰色地带”，始终将车停放在校园内部。

剔除不符合上述假设的数据，将符合上述假设的数据称为常规数据。在正常的情况下，共享单车的使用大部分为有规律的，与大部分学生的生活和作息相关，所以常规数据主要为非平稳序列。但由于个体的差异性，存在其他需求，所以常规数据中仍然会存在少量的白噪声序列。

3 非平稳序列的数据处理

数据的稳定性是时间序列预测的关键，一组数据的平稳性在于它在一段时间内围绕一个范围上下浮动，达到平稳要具备以下三个条件：

（1）数据的均值为常数：

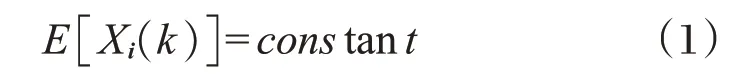
（2）方差为常数：

（3）任意相隔h个时刻的数据的协方差相同：

通过已知数据绘制折线图，可以看出大部分时间段，大部分地点，单车使用数据趋于平稳。对于已知数据中的非平稳的序列，采用差分进行预处理。

记∇为差分算子[2]，则一阶差分为：

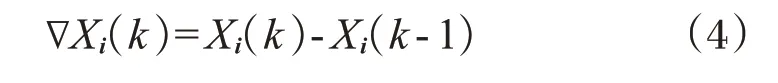
二阶差分为：

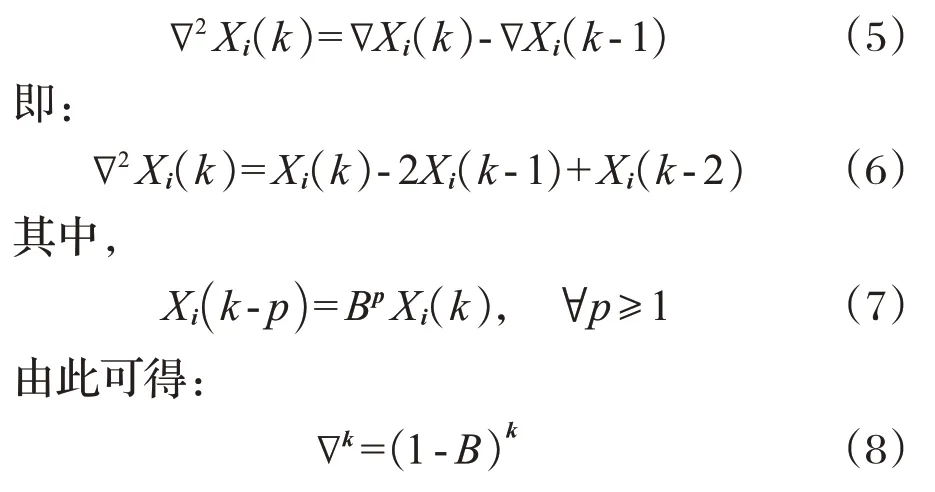
通常情况下进行一阶差分，如果一阶差分之后数据仍不平稳，可以再进行二阶差分。大多数情况下，数据在进行二阶差分下就平稳了。

4 基于时间序列预测的分析模型

时间序列预测是一种回归预测的方法，利用历史的数据，推测未来的数据发展趋势。有关时间序列预测的模型常见的有以下4种[3]：

（1）自回归（AR）模型：

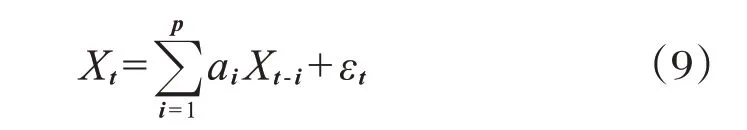
（2）滑动平均（MA）模型：

（3）自回归滑动平均（ARMA）模型：

（4）差分自回归滑动平均（ARIMA）模型：

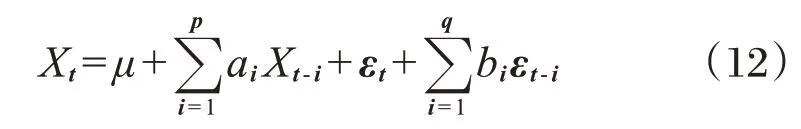
式中：Xt——时间序列值；εt——现在和过去的误差或冲击值；ai(i=1，2，…，p)——自回归系数；bi(i=1，2，…，q)——移动平均系数。

5 ACF/PACF的计算与ARIMA和AR算法模型选择

ACF是自相关系数序列函数，在时间序列内反映了Xt与Xt-k的相关程度，PACF是偏自相关函数，反映的是滞后值的相关性。通常情况下，平稳的序列自相关图有拖尾和截尾两种，拖尾有一个衰减的趋势，但不全为0，截尾指在某阶后，系数都为0。当自相关是拖尾、偏相关是截尾时，使用AR算法。当自相关是截尾、偏相关是拖尾时，使用MA算法，自相关和偏相关都是拖尾，则使用ARIMA算法。利用Matlab软件，分别画出11个地点的自相关图和偏自相关图，其中停车点1的自相关图如图2所示，停车点1的偏自相关图如图3所示。

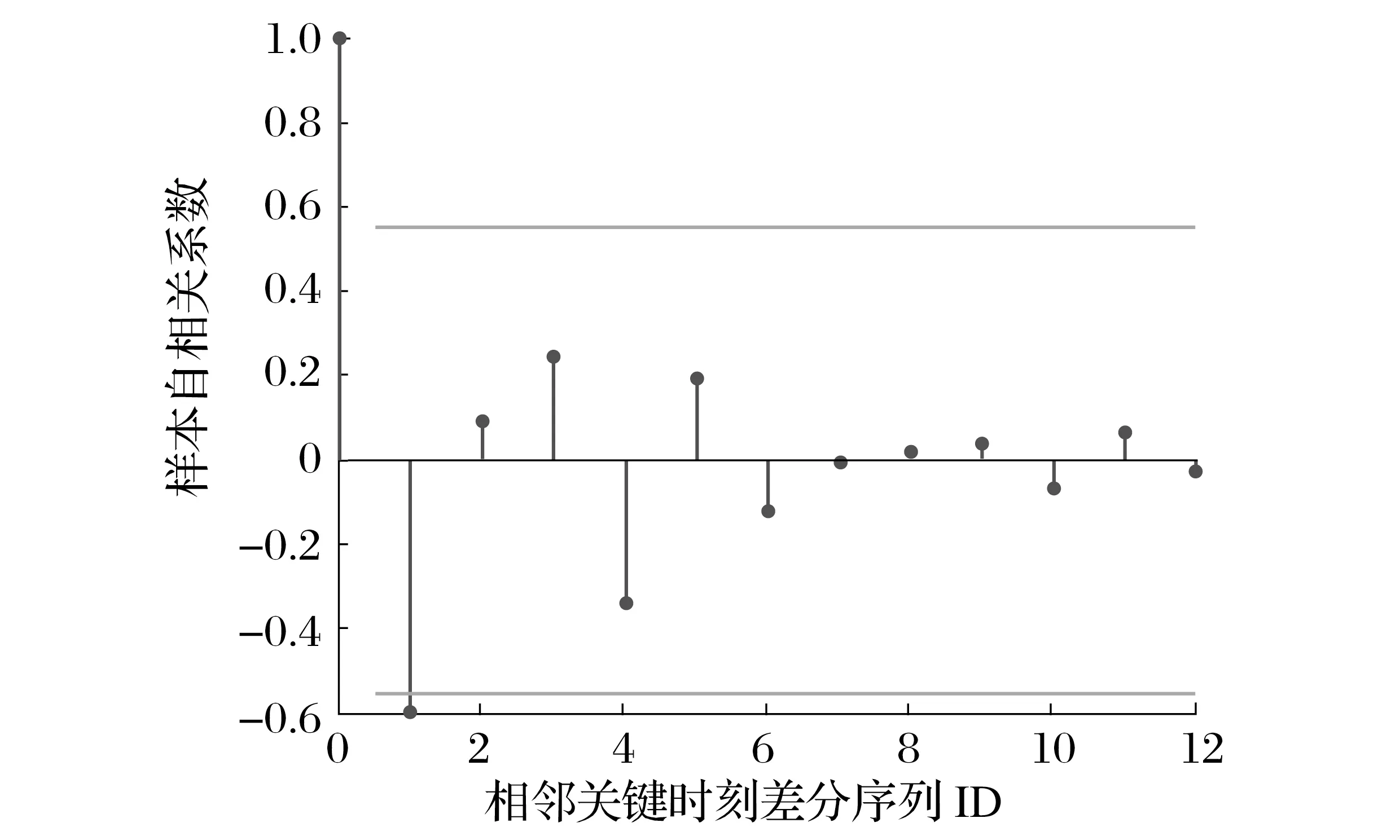
图2 停车点1自相关图

图3 停车点1偏自相关图

从各个停车点的自相关图和偏自相关图可见，11个停车点ACF均为拖尾，PACF为拖尾的有：1、3、4、5、6，PACF为截尾的地点有：2、7、8、9，其中10、11虽然为拖尾，但随着系数趋于0，可以近似为截尾。共享单车使用受时间相关性影响较大的还是教学楼、食堂、宿舍，而其余地点受时间相关影响相对较小，主要是受其他因素影响，具有随机性，也可以理解为白噪声扰动。

6 各停车点初始投放车数决策

根据ACF与PACF的结果，可以确定使用时间序列模型。对地点ID 为：1、3、4、5、6，使用ARIMA算法。对地点ID为：2、7、8、9、10、11，采用AR算法。各停车点各关键时刻的单车停放数目预测结果如图4所示。

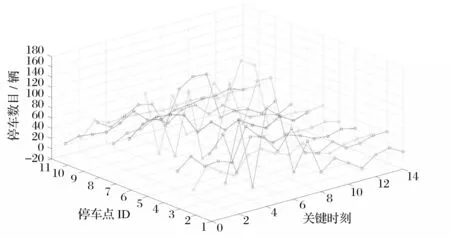
图4 未来一周各停车点各关键时刻共享单车数目预测

从图4可知，每个停车点不同关键时刻停车数目不同，在制定投放策略时，既要尽可能满足大学生骑行需求，也要考虑单车的损坏率。

根据经验，取s=0.20，计算得到未来一周各个停车点的单车投放数目，具体初始投放数目策略如表2所示。

表2 各停车点单车初始投放数目 单位：辆

从表2可知，博学楼投放量最大，达174辆，这是因为博学楼是全校的绝大部分课程的教学场所，其次是一期宿舍和二期宿舍，学生每天都要从宿舍出去，又要回到宿舍，投放量大是合理的。投放量最小的是两个校门，只有不到40辆，因校内生活配套齐全，无须频繁出校门。

7 结语

本文基于时间序列预测了校园共享单车停车数目，实际的校园共享单车使用情况较为复杂，很难满足上述全部假设，特别是停车点的不规律性以及单车损坏的随机性。因此，本文最终所给出的投放策略刻意加大了初始投放数目，尽可能满足学生的骑行需求。共享单车在大学校园的投放离不开学校的资金投入和相关政策的实施，共享单车的停车点选址有待进一步深入研究。