运载火箭动力系统故障下制导控制技术研究进展

李爽，刘旭，叶松，林子瑞

运载火箭动力系统故障下制导控制技术研究进展

李爽1，刘旭1，叶松2，林子瑞1

（1.南京航空航天大学 航天学院，江苏 南京 211106；2.北京航天自动控制研究所，北京 100854）

动力系统故障是导致运载火箭发射任务失败的最常见原因，从动力系统故障建模、自主制导和容错控制方面，系统地阐述了动力系统故障下运载火箭制导控制技术的研究进展，为发展新型制导控制算法提供了思路。建立了推力下降故障和执行机构故障的数学建模，并对比了国内外先进运载火箭的制导控制性能；总结了动力系统故障下自主制导所涉及的轨迹优化和制导算法；在被动、主动容错控制框架内，回顾了典型的故障诊断、控制重构、容错控制和震动抑制方法；同时，概述了人工智能技术在自主制导和容错控制方面的应用；结合“会学习”的运载火箭概念，讨论了人工智能技术在促进运载火箭自主化和智能化方面的发展趋势，对未来智慧火箭的制导控制技术进行了展望。

运载火箭；动力系统故障；故障诊断；制导控制；人工智能

0　引言

截至2022年初，全球运载火箭发射任务已经超过6 000次，但失败也超过500次，尤其是近年频繁发生运载火箭发射失利的情况［1］。以2021年发射情况为例，美国RocketLab公司的电子号火箭二级发动机点火异常导致关机；阿斯特拉公司的Astra Rocket 3.3火箭一级发动机起火爆炸［2］；而我国星际荣耀公司的双曲线一号火箭的一级和三级发动机异常关机导致2次发射失利；快舟一号甲运载火箭因为发动机故障而发射失败。

导致运载火箭发射失利的原因主要有3类［3］：分离系统故障、制导控制系统故障和动力系统故障。分离系统故障主要包括逃逸塔分离失败、整流罩分离失败、级间分离失败与星箭分离失败。制导控制系统故障包括执行机构卡死故障和控制系统开环故障。动力系统故障包括运载火箭发动机推力下降故障、异常关机、未成功点火、爆炸。上述故障按照故障的能量属性可大致划分为4类［4］：

1）非（微）能量故障包括制导控制系统部分信息错乱、丢失等；

2）小型能量故障包括某级推力小幅下降且超过预期阈值、部分助推器未按预期时间分离等；

3）中型能量故障包括某级推力非预期大幅下降、执行机构部分卡死等；

4）大型能量故障包括火箭爆炸、某级推力完全丧失、执行机构完全卡死、级间未分离等。

以上4类故障除大型能量故障为致命故障外，其余均为非致命故障。尽管非致命故障不会导致箭体爆炸或解体等严重事故，但不及时采取救援措施将导致发射任务失败。例如，2017年7月发射的长征五号火箭飞行至346.7 s后一台发动机出现故障，火箭仍旧按照原有制导和控制方案飞行，导致二级飞行未能飞出大气层，最终任务失败。如果能及时调整制导和控制方案，则仍有可能在出现非致命故障时提升运载火箭的发射成功率。1964年，美国土星一号运载火箭在飞行117 s后，一台发动机异常关机，通过调整运载火箭的飞行程序，利用剩下 7台发动机进入原定轨道，最终完成了预设任务目标。2012年，Falcon 9运载火箭执行发射任务，在发射79 s后，其中一台发动机发生故障关机，随后通过在线轨迹重构使得运载火箭的载荷成功进入原定轨道，完成飞行任务。Falcon 9搭载的9台发动机形成动力冗余架构，保证了飞行全程1台发动机故障、飞行90 s后2台发动机故障都不影响完成发射任务［4］。

尽管土星一号和Falcon 9火箭在发生推力下降故障情况下成功完成发射任务，但并不意味着它们具备制导律重构和容错控制能力，因为上述火箭在设计时就增加了1台发动机用来提供运载能力冗余，以确保动力系统故障后仍能将载荷送入原定轨道［4］。我国长征系列运载火箭由于发动机结构布局难以增加1台发动机，运载能力冗余较小。随着运载火箭载荷的不断增大，通过增加发动机的硬件冗余方式已经无法应对非致命故障下的安全需求。因此，发展具有自主制导和容错控制能力的方法以提高运载火箭的生存概率势在必行。

本文从动力系统故障建模、自主制导和容错控制3方面，系统地回顾了运载火箭动力系统故障下制导控制技术的进展，并结合人工智能技术进行了展望，总体框架如图1所示。

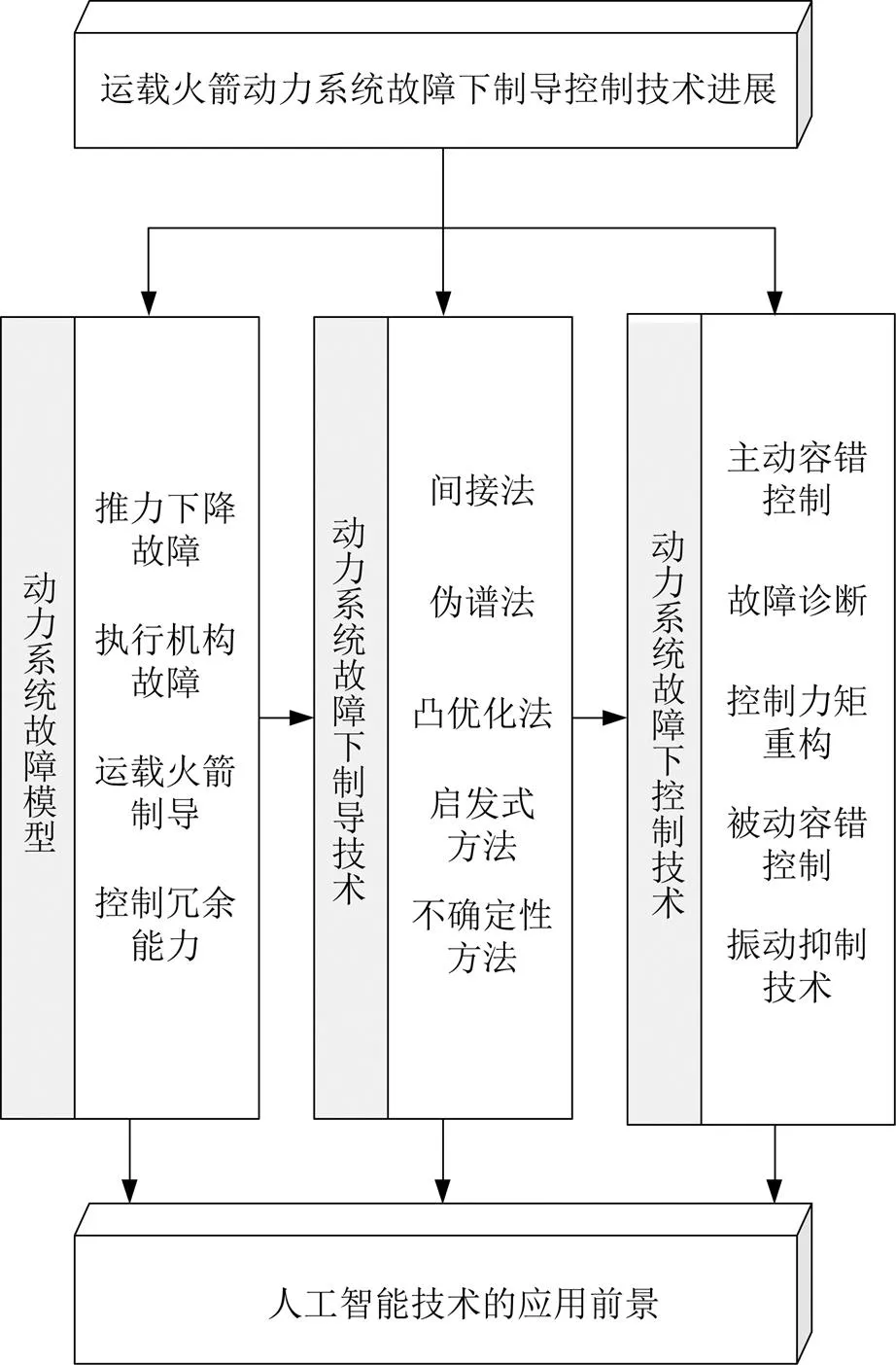
图1　运载火箭动力系统故障下制导控制技术进展概览

1　动力系统故障模型

运载火箭非致命故障以动力系统推力下降、发动机摆角执行机构故障最为常见，主要考虑以上 2类故障的建模问题。

1.1　推力下降故障

运载火箭推力下降故障主要考虑2类故障模式［3］，运载火箭发动机推力下降为发动机额定推力的比例值和运载火箭发动机推力持续线性下降至一定推力值。第1种故障模式也称为推力比例下降；第2种故障模式也称为推力线性下降。2类故障如图2所示。

图2　运载火箭推力下降故障

1）推力比例下降模型

运载火箭发动机推力比例下降故障的数学模型如下：

式中：为飞行时间；为运载火箭发动机实际推力；0为发动机额定推力；1为发动机发生推力比例下降故障后发动机实际推力；1为发动机故障发生的时间。

2）推力线性下降模型

运载火箭发动机推力线性下降故障的数学模型如下：

式中：2为发动机发生推力线性下降故障后发动机实际推力大小；2为发动机推力线性下降故障的发生时间；3为发动机推力线性下降故障的稳定时间。

1.2　执行机构故障

运载火箭发动机摆角执行机构故障会影响发动机输出摆角大小，进而影响运载火箭推力的大小和方向，导致轨迹和姿态控制失稳。摆角执行机构常见的故障主要包括卡死、松浮、损伤及饱和故障［5-6］，故障模型如图3所示。

图3　运载火箭执行机构故障［6］

1）卡死故障。卡死故障是指发动机摆角执行机构长期保持在某一非0位置，无法响应控制指令，但仍输出常值摆角。

2）松浮故障。松浮故障是指执行机构发生松动，一直保持在0位置，无法响应控制系统指令。

3）损伤故障。损伤故障是指执行机构的控制增益发生变化，导致响应控制指令后产生偏差，导致控制性能降低。

4）饱和故障。饱和故障是指执行机构长期响应到正向或负向最大位置。此类故障中执行机构无法满足控制指令需求。

运载火箭摆角执行机构故障模型如下：

式中：0为执行机构的0位置；max、min分别为执行机构的最大、最小值；c为正常情况下执行机构的输出量；c1、c2、c3和c4分别为卡死、松浮、损伤和饱和故障下执行机构的输出量；c1、c2、c3和c4分别为摆角执行机构发生卡死、松浮、损伤和饱和故障的时间。

1.3　运载火箭制导控制冗余能力

现役的运载火箭一般依赖动力系统硬件冗余和姿态控制系统的相位裕度来包容动力系统故障，但只适用于非能量故障和部分小型能量故障。以我国长征系列运载火箭为例，其制导控制系统主要由分系统级信息管理系统、控制系统冗余架构和制导控制算法构成，通过配置双通道或三冗余总线、箭机、惯组等实现故障诊断和控制重构，由于缺乏全箭级的系统管理能力，只能应对故障引起的小偏差问题［7-9］。国外新型运载火箭（如太空发射系统SLS和Falcon系列火箭）配置了全箭级信息管理系统和鲁棒性较强的制导控制算法，对于较大的推力下降故障和发动机摆角执行机构卡死、失效等故障，有一定的适应能力。国内外运载火箭制导控制系统性能对比见表1［8-10］。

表1　国内外运载火箭制导控制系统性能对比

由表1可知，国外运载火箭的优势在于成熟的信息管理系统和制导控制算法，在硬件冗余方面和国内“长征”系列运载火箭差距不大。通过增加硬件冗余提升制导控制系统品质的方式已经基本到达上限，继续增加硬件反而会使控制逻辑庞杂和运载能力下降，而发展更加自主、容错的制导控制算法将在不增加硬件的情况下有效提升运载火箭的自主任务规划和在线控制重构能力，是未来运载火箭发展的新方向。

2　动力系统故障下制导技术

运载火箭制导技术包括轨迹优化和制导算法。制导算法也称制导律，用于生成运载火箭从地面转移到目标轨道所需的制导指令，具有实时性和鲁棒性，但不一定最优。轨迹优化算法通常不考虑飞行系统内部模型或参数的误差以及外部扰动，经离线或在线计算得出满足运载火箭上升、入轨约束条件的最优轨迹，等价于开环制导算法。在实际任务中，轨迹优化是制导的基础环节，如为制导算法提供参考轨迹或直接作为制导律生成制导指令，因此本文对两者不加区分，统称为制导算法。

早期运载火箭以程序制导方案为主，通过姿态控制系统跟踪离线规划好的程序角实现飞行剖面控制。该方法属于开环制导，无法根据飞行状态实时更新程序角指令，自主性差。目前，运载火箭大多采用摄动制导和迭代制导的组合方案。在大气层内，摄动制导将实际轨迹在参考轨迹附近取一阶近似，然后根据制导精度和特定飞行状态的误差量设计反馈控制增益，使运载火箭尽可能飞行在参考轨迹附近［11］。在大气层外，迭代制导将入轨位置和速度矢量作为约束条件，基于最优控制理论推导闭环解析解，逐渐消除摄动制导的误差后实现精确入轨。摄动制导易于实现，对计算性能要求不高，但发生推力下降故障或外界干扰明显时，运载火箭的飞行剖面将大幅偏离参考轨迹，无法满足一阶线性假设，进而使导引系数的修正能力饱和，并最终使运载火箭偏离目标轨道，甚至引发箭体失衡［12］。因此，提高制导系统应对动力系统故障的能力是当前制导技术的研究热点之一。

2.1　间接法

间接法以最优控制理论为基础，将最优轨迹优化问题转变为两点或多点边值问题，然后求解。早在20世纪60年代，LAWDEN［13］基于最优控制理论得出了真空状态下常值推力火箭入轨的最优推力方向和速度协态变量位于同一方向的结论，该结论也被称为“主矢量”理论。CHANDLER等［14］基于平坦地球假设推导了解析的线性正切制导律，并进一步发展为迭代制导。目前，包括迭代制导、真空最优制导（Vacuum Optimal Guidance，OPGUID）和动力显式制导（Powered Explicit Guidance，PEG）等方法已经成为运载火箭大气层外制导的主流算法。随着箭载计算机技术的发展，采用打靶法、有限差分法等数值方法求解两点边值问题成为可能［15］。CALISE等［16-17］将真空最优制导的解析作为大气层内轨迹优化问题的同伦初值，采用配点法求解了对应的两点边值问题，能够在线生成满足过程约束的制导指令，同时也将该方法用于运载火箭发射逃逸轨迹的设计。DUKEMAN和GATH等［18-20］将这一方法扩展到包含滑翔过程的运载火箭上升制导中。PU等［21-22］和PAN等［23］则进一步结合有限差分和大气密度同伦技术对CALISE的工作［16-17］进行提高，实现大气层内助推-滑翔上升和大气层外入轨全过程的在线轨迹优化与闭环制导。HANSON等［24］从路径约束满足情况、计算量等方面定量评估了基于间接法的运载火箭制导律，结果表明，真空最优解可作为大气层内闭环制导的初始猜测值，缩短了发射准备时间，并满足过载、动压、入轨条件等约束，且具备应对动力系统非致命故障的潜力。但是间接法应用于在线轨迹或制导指令生成时的收敛性和稳定性有待提高。

为提高动力系统故障下运载火箭的安全性和成功率，近年来研究人员对间接法进行了改进。 湛康意等［25］针对推力下降故障，设计了以入轨点高度为自变量的特征量函数来评估运载火箭剩余入轨能力，并采用真空最优制导算法实现目标轨道和救援轨道的入轨，但仅固定了目标轨道倾角，没有考虑升交点赤经约束。李文清等［26］基于迭代制导算法，分析了不同推力下降故障发生时运载火箭的剩余入轨能力。韩雪颖等［27］则进一步采用迭代制导算法构建了运载火箭推力下降故障轨迹数据库，通过遥测数据判断是否修改迭代制导算法的发射诸元来进入救援轨道。WANG等［28］为了确定助推-滑翔-助推运载火箭进入预定目标轨道的故障状态集，提出了一种基于迭代制导和牛顿法的转移轨道快速重规划方法，将复杂的多段轨道规划问题转化为转移轨道搜索问题，可快速求解。

2.2　伪谱法

伪谱法是将状态量和控制量在全局正交节点上离散，从而把最优控制问题转化为参数优化问题，再采用非线性规划算法求解。该方法具有处理约束能力强、收敛精度高的特点，在2000年前后大规模应用于航空航天轨迹优化和制导领域。在运载火箭轨迹优化方面，RAO等［29］基于伪谱法开发了轨迹优化软件GPOPS，并求解了多级运载火箭大气层内发射的问题。MA等［30］采用自适应伪谱法研究了多级运载火箭不同故障程度下的在线轨迹重规划方案。LIU等［31］为提高Gauss伪谱法的计算效率，提出了初值-终值迭代方法，将不考虑性能指标的最优解作为燃耗最优问题的初始猜测值，该方法有效地提升了最优轨迹计算效率，但仍无法实现在线轨迹优化。马林［32］采用自适应Gauss伪谱法求解了运载火箭六自由度轨迹优化问题。王志祥［15］以故障时刻的飞行状态为初值，结合助推段飞行终端约束，采用Gauss伪谱法完成了最优轨迹重构。但该方法无法保证任何故障状态下运载火箭仍能进入目标轨道，且轨迹优化时间不符合在线轨迹重构要求。张志国等［33］采用C语言版SNOPT求解器，通过调整Gauss伪谱法的节点数目和制导周期，在满足入轨精度和终端约束的同时提高了计算效率，满足了在线轨迹规划需求，但节点数目和制导周期的确定依赖前期大量仿真，通用性和自主性较差。HE等［34］为解决推力下降故障下运载火箭无法入轨的问题，基于自适应配点法离线生成了故障下的最优救援轨道和上升轨迹，使用深度神经网络映射故障状态与最优救援轨道根数和终端控制变量的关系，确定不同故障状态下应进入的救援轨道，最终采用自适应配点法完成上升轨迹重构。

目前，伪谱法的发展已不再局限于直接配点法的思路。FARHOO等［35］和YAN等［36］提出了只需要进行简单矩阵运算便可以获得跟踪制导指令的间接伪谱法。随后TIAN等［37］和LIAO等［38］等分别将间接Legendre伪谱法和间接Radau伪谱法用于大气再入跟踪制导。同时，经典伪谱法也常常和滚动时域控制结合，用于设计运载器大气再入跟踪制导律。此外，YANG等［39］和RAHMAN等［40］等也开发了不依赖参考轨迹的伪谱模型预测制导算法，实现了大气层外运载火箭自适应制导，将有望应用于推力下降故障场景。MA等［41］采用投影牛顿型方法改进了并行牛顿型制导方法，并将其用于在线求解运载火箭动力下降故障下时间自由轨迹重规划问题。尽管间接伪谱法和基于经典伪谱法的模型预测控制算法在运载火箭轨迹优化方面应用较少，但大气再入和上升2类场景互为逆过程，因此该思路也可推广到运载火箭制导领域。

2.3　凸优化方法

凸优化方法通过凸松弛、无损凸化等手段，将非凸优化问题转化为凸问题求解，由于凸优化理论具有理论全局最优性和多项式计算复杂度的优势，在飞行器轨迹优化和制导领域得到了广泛关注。美国国家航空航天局（National Aeronautics and Space Administration，NASA）和太空探索技术公司为Falcon 9火箭垂直着陆开发的制导算法G-FOLD就采用了凸优化方法［42］。CHENG等［43］在研究火箭最优上升制导问题时采用Newton-Kantorovich迭代法对系统动力学进行线性化，再使用序列凸优化法进行求解，同时给出收敛性证明，算法计算耗时约 2～3 s。王嘉炜等［44］在CHENG研究成果的基础上向性能指标中加入邻近规则化项，采用Proximal-Newton-Kantorovich迭代法对动力学进行线性化，计算效率进一步提高到1 s。SUN等［45］在序列凸优化方法的基础上，引入了收缩信赖域策略，提高了算法求解效率，但只求解了运载火箭在弹道平面内的上升制导问题。ZHANG等［46］考虑了火箭上升过程中的阻力，采用序列凸优化方法求解了发射平面内的上升轨迹。BENEDIKTER等［47-48］结合序列凸优化和同伦策略，提出了用于解决运载火箭大气层内时间最优轨迹优化问题的凸优化算法。李敏等［49］将火箭制导控制一体化动力学模型反馈线性化，从而将非凸轨迹跟踪问题转化为凸优化问题，并在模型预测控制框架下实现鲁棒制导，但只研究了弹道平面内的跟踪制导问题。近期，伪谱凸优化凭借更高的计算精度和计算效率得到关注。在运载火箭轨迹优化方面，王洪波等［50］采用LGR伪谱凸优化方法，并将滑行时间增广为控制变量，解决了固体燃料运载火箭入轨制导的点火时间不确定问题。

此外，李师尧等［51］将二维简化模型下的优化结果作为推力故障下轨迹重构问题的初值，通过凸优化求解了燃耗最优的最高圆轨道或椭圆轨道。 宋征宇等［52］在故障时估计地心角和凸优化计算最高圆轨道，并将其作为自适应伪谱法的初值，进一步求解不含地心角约束的最高圆轨道用于决策是否调整轨道根数。LI等［53］结合无损凸优化和序列凸优化方法，求解了推力下降故障下运载火箭轨迹优化问题，使运载火箭进入最优或次优轨道。 LI等［54］进一步提出间接凸优化方法，但只适用于大气层外轨迹优化。MIAO等［55］引入虚拟控制量来弥补推力故障导致的火箭加速度损失，通过求解凸优化问题来判断推力故障下运载火箭是否能进入目标轨道。SONG等［56］为解决推力下降情况下运载火箭目标轨道与飞行轨迹的在线联合优化问题，提出了状态触发指标以提高求解效率，包括用于计算推力下降时轨道面内最高圆轨道、椭圆轨道的最优高度指标，以及寻找非共面最高椭圆轨道的最小轨道平面偏差指标，进而构造了近似子问题来初始化凸优化算法，使得最优轨迹收敛于最优或次优解，避免了推力下降导致轨迹重构问题无解。

2.4　启发式方法

启发式方法通过模拟物理或生物规律实现问题寻优，主要包括模拟退火算法、粒子群算法、遗传算法、哈里斯鹰算法、鲸优化算法等。由于发展较早，已有大量文献将启发式算法用于运载火箭轨迹优化。罗亚中等［57］为二级运载火箭提出了基于轨道分解优化和遗传算法（Genetic Algorithm，GA）的太阳同步轨道任务发射轨迹设计方法。胡凡等［58］将自适应遗传算法优化的结果作为序列二次规划的优化初值，以起飞质量为目标函数，研究了固体燃料运载火箭轨迹和参数一体优化的问题。杨希祥等［59］通过改进控制参数和引入函数拉伸策略，对粒子群算法进行了改良，并求解了固体燃料运载火箭上升段程序角优化问题，同时阐述了智能算法在飞行器轨迹优化中的应用。张柳等［60］改进了PSO-Powell算法的参数设置，并引入增广拉格朗日乘子处理运载火箭上升段的过程约束，取得了良好的效果。高哲等［61］将最大有效载荷作为优化目标函数，研究了罚函数法、粒子群算法和Powell法在多级固体燃料运载火箭轨迹优化问题中的性能。李晓苏［62］采用多目标启发式算法对运载火箭轨迹规划问题进行研究，从算法的计算时间、收敛性和收敛速度等方面进行分析评估。根据现有研究可知，启发式算法一般用于运载火箭发射前总体参数和参考轨迹的优化，在应对动力系统故障方面作用不大。

2.5　不确定性方法

有别于确定性优化问题，不确定性优化问题考虑了系统参数、初始条件等因素的误差，研究系统在误差条件下的演化。主要的不确定性优化方法包括鲁棒优化、协方差分析、系统灵敏度理论、不确定性量化等。ROSE等［63］将线性协方差技术应用于动力显式制导，开发了快速确定轨迹控制误差、推进剂偏差、入轨偏差、导航误差，以及传感器误差、执行器不确定性和随机干扰灵敏度的仿真工具，可用于多级运载火箭发射前任务分析。倪彧祺［64］在考虑运载火箭模型参数不确定性的情况下使用协方差矩阵方法设计了闭环制导律，有效抑制了模型参数误差对入轨精度的影响。SHEN等［65］基于系统灵敏度理论提出了脱敏最优控制，通过引入微分黎卡提方程实现了火箭在各类不确定性条件下的垂直闭环着陆，该算法可推广到运载火箭上升轨迹优化和制导问题中。ZHANG等［66］分析了模型参数、外界干扰等不确定性因素对运载器轨迹优化的影响，并采用基于灵敏度非线性规划求解器sIPOPT的Gauss伪谱法求解了运载器轨迹优化问题。但是非确定性优化方法很少考虑动力系统非致命故障。

2.6　制导技术小结

综上所述，现有制导方法的总结见表2。

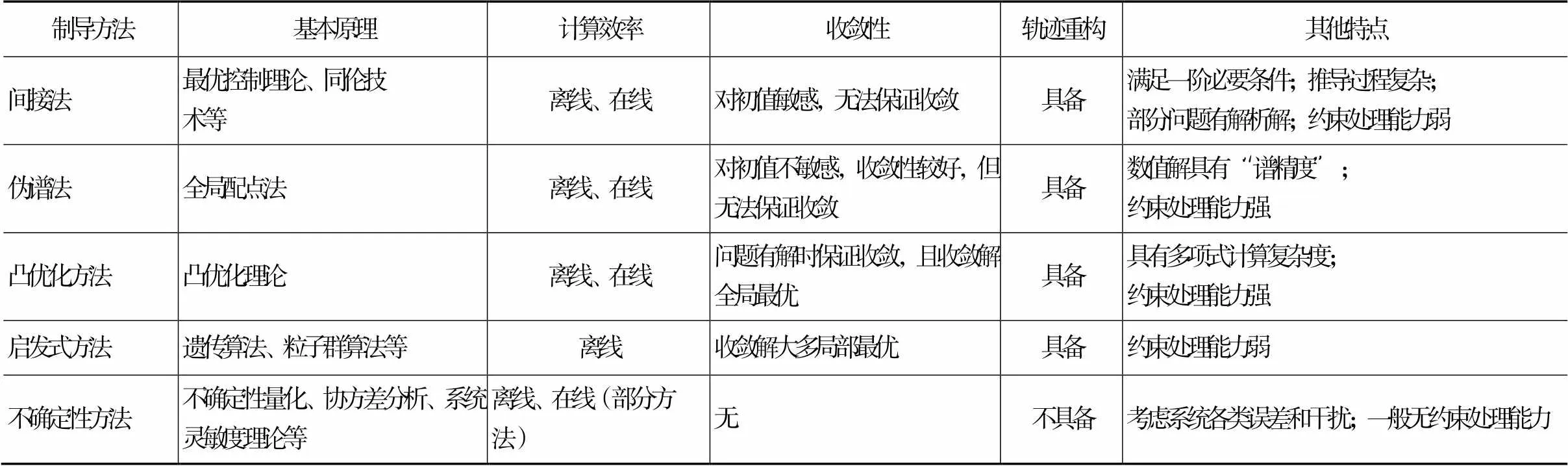
表2　制导方法性能对比

目前，自主制导是运载火箭动力系统故障下制导技术的研究热点，该方法根据飞行状态实时规划满足后续过程约束和终端条件的飞行轨迹，并生成当前制导指令。自主制导可以处理复杂、时变的非线性约束，具有很强的适应性和鲁棒性。通常，具有同一概念的方法也被称为计算制导、在线轨迹优化、自主任务规划、自适应最优制导、端对端规划、容错制导等［52］，但自主制导对于制导律的计算效率和可靠性有较高的要求，因此提高算法的计算效率和收敛性是后续发展运载火箭动力系统故障下制导技术的关键。

3　动力系统故障下控制技术

运载火箭发动机推力下降，或者摆角执行机构卡死、饱和、损伤等故障时容易导致运载火箭姿态控制系统的控制精度下降，而未建模或建模不充分的弹性震动和液体晃动可能覆盖控制指令，因此要求运载火箭姿态控制系统具备容错和抗干扰能力。为避免动力系统故障给运载火箭姿态控制系统造成严重影响，通常采用硬件冗余和解析冗余方案提高运载火箭姿态控制系统的性能。硬件冗余是指在设计姿态控制系统时额外增加若干个机构，当部分机构发生故障时剩余的机构仍能保证控制系统稳定［67］。解析冗余则通过设计恰当的控制器，最大限度地利用控制能力，提高姿态控制系统应对故障的能力。硬件冗余只需要在发生故障时启用备份硬件即可，对控制器的设计没有特殊要求。解析冗余又称主动冗余或容错控制，根据故障信息来改变控制器参数或结构，从而充分利用系统控制能力实现故障在线补偿。目前，运载火箭动力系统故障补偿成功案例基本上都是基于动力系统硬件冗余实现的，即关闭故障发动机后对其他并联发动机进行调节，以补偿发动机故障造成的推力减少和推力方向偏差。但运载火箭的发动机和执行机构等硬件冗余已经达到上限，难以通过继续增加冗余度来提高制导控制品质，因此，解析冗余是当前研究的重点。

解析冗余的实现方式较多，根据是否需要准确的故障信息，可将解析冗余方法分为2类：1）依赖在线故障诊断信息对系统控制力矩进行重构，使得系统在故障情况下仍能保持高精度稳定，该方法根据故障信息主动调整了控制律，也被称为主动容错控制；2）不依赖精确的故障信息，而是通过自适应或鲁棒策略，根据故障下状态量的变化情况进行控制律参数在线调节，从而保持控制系统稳定，也被称为被动容错控制［6］。因此，运载火箭控制技术的研究方向主要包括故障诊断技术、控制力矩重构技术，以及被动容错控制技术。此外，鉴于控制模型中未建模动态给姿态控制系统造成的干扰，控制系统对箭体震动的抑制技术也是研究的重点。

3.1　故障诊断技术

故障诊断技术是火箭发动机健康管理系统的核心，是基于数据、知识和模型的故障诊断算法，用于飞行、试车和试车后的发动机故障诊断与分析［68-69］。对于飞行过程中发生的动力系统故障，由于运载火箭难以测量全部信号且地面测控系统也无法及时处理回传信号，因此自主故障诊断技术非常重要。

自主故障诊断系统应具备自主故障检测、估计和定位能力，其中故障检测和估计反映了故障是否发生以及严重程度，故障定位则需要确定故障的位置并将其从控制系统中隔离［70-72］。常用的自主故障诊断方法是基于冗余信息的处理与自检测技术，主要依据交叉检查、一致性检查、表决机制等策略，已经得到实际应用。

基于知识和数据的方法受限于箭上计算能力而发展较慢。目前，自主故障诊断主要依赖基于模型的算法［69］。自主测试工程师（Knowledge-based Autonomous Test Engineer，KATE）方法是基于模型的算法之一，该方法建立发动机的标称模型和故障模型，通过数学仿真发现和定位故障。随着控制理论的发展，基于滤波器、系统辨识和最优化等方法的故障诊断方法逐渐发展起来。符文星等［73］基于简化的运载火箭6自由度模型，在扩展卡尔曼滤波中引入时变遗忘因子，实时调整状态预测误差协方差矩阵的大小，从而调整滤波器增益矩阵以提高滤波器对推力突变故障的适应能力。在此基础上，ZHANG等［74］则通过扩展卡尔曼滤波计算俯仰角速度的残差，采用灵敏度分析方法确定残差和推力下降比例之间的关系式，并根据箭体法向过载信息确定故障发动机位置。叶松等［70］在此基础上采用滚动二次规划方法代替最小二乘方法估计了推力下降的程度。CHEN等［75］则基于运载火箭模型，使用跟踪微分器估计故障情况下角加速度，通过对比故障下和非故障下的角加速度来判断是否发生故障，并引入带有遗忘因子的最小二乘算法和加速度信息实现推力下降故障程度和位置的估计。CHA等［76］建立液体燃料发动机的非线性模型，结合扩展卡尔曼滤波和无迹卡尔曼滤波设计了多模型滤波器用于检测发动机故障。LEE等［77］为进一步实现发动机稳定工作情况下的故障，将发动机模型线性化，基于卡尔曼滤波、阈值测试、白度测试、广义似然比测试和多模型方法设计了故障诊断算法，能够快速准确地定位发动机涡轮效率下降故障。孙成志等［78］基于神经网络和证据理论，采用径向基神经网络建立火箭视加速度、角速度和故障类型矩阵的映射关系来完成火箭发动机故障诊断，随后基于D-S证据理论融合故障诊断结果，并通过扩展卡尔曼滤波完成火箭飞行状态特征量估计，确定运载火箭推力下降比例或执行机构是否卡死。王硕等［79］联立角速度和视加速度的状态方程，构造了卡尔曼滤波的测量方程，采用带有遗忘因子的最小二乘算法估计了推力下降程度，算法具有一定鲁棒性。赵万里等［80］为解决某型液体燃料火箭发动机的实时故障诊断问题，基于现有发动机模型和传感器数量，设计了一种递归结构识别算法。该方法采用自适应学习网络建立了传感器输出信号和发动机响应量之间的最优预测模型，若预测响应和实际响应的误差超过阈值，则判断发动机发生故障，再根据平均绝对误差完成故障定位，算法在FPGA和DSP双系统平台上部署后可在 6 ms内诊断出发动机流量衰减故障。

3.2　控制力矩重构技术

控制重构技术是根据故障信息对控制器的参数或结构进行在线调整，可以充分利用系统的控制能力来减小甚至消除动力系统故障的不良影响。在航空航天领域，控制重构技术主要用于卫星姿态喷管故障重构、飞机或运载器气动舵面故障重构。控制重构技术主要有广义逆、线性规划、二次规划、凸优化、神经网络等方法［15，67，81］。尹彪等［82］针对运载火箭发动机摆角发生卡死故障，对摆角进行重新分配后实现了控制力矩重构，但没有考虑摆角速率和摆角幅值等约束。黄盘兴［67］以重构力矩误差为目标函数，构造了二次规划问题，采用不动点迭代法进行求解，相比经典伪逆法可以避免执行机构饱和。孟洲［81］将芯级和助推级进行联合分配，通过广义逆法实现控制力矩重构，避免了运载火箭执行机构卡死导致的姿态失稳。李铸［83］将重构力矩误差最小问题松弛为一个凸优化问题，采用凸优化方法求解，满足控制约束的同时保证误差最小，但计算效率有待提高。

进一步采用神经网络建立了故障程度和重构最优解之间的映射网络，实现在线重构。冯昊等［84］基于故障补偿思想，开展了执行机构卡死故障下的大推力运载火箭控制分配研究，但未考虑执行机构的幅值和速率饱和。程堂明等［85］采用线性规划控制方法进行运载火箭摆角分配，系统容错性能提高，但该方法计算耗时较长。余光学等［86］通过引入非负松弛变量，将等式和不等式约束统一为等式约束，将发动机摆角控制分配问题转化为线性规划问题求解。ZHANG等［87］针对推力下降故障下运载火箭姿态跟踪控制问题，提出了结合级联伪逆分配方法和神经元自适应增益调度方法的两级控制力矩重构方案，同时针对一些典型的故障场景，提出了基于控制状态可达性的故障系统重构方法，该控制重构策略能有效地处理推力损失故障，实用性较好。于海森等［88］将运载火箭控制力矩重构问题描述为约束二次规划问题，并采用基于Armijo搜索准则和BFGS算法相结合的控制分配算法进行求解，该方法在单台发动机故障下具有良好的姿态控制精度。WEI等［89］基于自适应非奇异快速终端滑模控制律，提出了一种基于加速Landwber迭代的控制分配算法，根据执行机构的有效增益以及执行机构当前位置到相应饱和极限的距离来确定控制比例分配，同时将过饱和指令在正常执行机构之间进行再分配，可用于执行机构发生故障时对控制器进行在线重构。综上所述，控制力矩重构多采用基于优化的策略，通过优化发动机摆角来实现重构力矩误差最小。该策略能够处理摆角幅值、摆角速率等约束条件，因而得到广泛关注，但计算效率有待提高。

3.3　被动容错控制技术

被动容错控制技术在运载火箭姿态控制技术领域发展较快，主要方法有自适应控制、鲁棒控制、滑模控制、模型预测控制等［6］，但现有研究大多考虑干扰、模型参数或结构不确定性对控制系统性能的影响，而很少研究执行机构故障问题。典型的运载火箭被动容错控制系统是NASA为太空发射系统（Space Launch System，SLS）开发的自适应增广控制（Adaptive Augmented Control，AAC）方法［90-92］，该方法根据MH-90等飞机的自适应驾驶系统开发，结合了PID控制和自适应技术。当运载火箭处于标称飞行状态且外部干扰较小时，由PID控制器单独控制，而当外部环境对火箭产生明显干扰，导致模型结构或参数发生较大改变时，自适应控制将通过系统辨识方法修改模型，并联合PID控制器调整控制指令，因对控制系统中未知或未建模动态、非线性和环境干扰具有很好的鲁棒性［6，93-94］。NASA从2012年开始系统测试自适应增广控制技术在运载火箭控制系统中的应用效果，先后开展了数值仿真、F-18飞行测试和全面安全性评估，测试结果表明，AAC方法对于闭环不稳定情况具有抑制作用，具有从低控制性能中恢复、防止或减少火箭控制系统失效的能力，有效地增强了系统的稳定性和鲁棒性［90-92］。目前，AAC方法已经用于SLS的无人飞行测试。TROTTA等［95］对AAC方法进行了改进，提出采用鲁棒优化方法替代AAC的参数整定工作，分别采用基于遗传算法和Min-max策略对这一鲁棒优化问题进行求解。仿真结果表明，运载火箭在故障和干扰情况下的姿态稳定概率达到94%。 崔乃刚等［97］为自适应增广控制增加了干扰补偿回路和主动减载回路，明显提高了运载火箭在内部参数、外界风干扰和弹性震动影响下的适应能力。

除AAC方法之外，LEFEVRE等［91］针对Ares-I火箭的弹性抑制问题，设计了基于误差四元数和神经网络的自适应PID控制器，当推力下降10%时取得比传统增益调度和PID控制律更好的跟踪效果。梁小辉等［98］采用自适应和滑模变结构控制，设计了容错控制律，保证了运载火箭发动机摆角执行机构发生故障时姿态跟踪误差有限时间收敛，同时结合了自适应动态规划方法对姿态跟踪误差进行补偿。ZHANG等［99］设计了固定时间扩张状态观测器（Fixed-Time Extended State Observer，FxTESO），用以估计运载火箭姿态跟踪误差的导数和外界干扰，结合具有自适应增益的非奇异快速终端滑模方法（Nonsingular Fast Terminal Sliding Mode Scheme，NFTSMS）提出了一种自适应容错控制方案，该方案对多种干扰和栅格翼的执行器故障都具有鲁棒性。马艳如等［100-101］考虑干扰和执行器故障，采用非奇异终端滑模方法解决了运载火箭姿态系统跟踪问题，获得了较好的抗干扰和故障容错能力，并使用自适应径向基神经网络逼近外界干扰和内部故障造成的力矩增减量，进而对控制力矩指令进行补偿，避免姿态跟踪误差因干扰和执行机构故障而发散。朱海洋等［72］针对运载火箭推力下降或执行机构卡死等故障，提出了构建基于RBF神经网络的在线辨识模型，并结合滑模变结构控制设计了基线控制器对故障模型和干扰进行辨识和补偿，实现建模偏差较大、单台执行机构卡死和芯级单台发动机推力下降多种故障工况下姿态控制系统的稳定。苏秀健［102］针对发动机执行机构卡死故障，采用二次规划方法进行摆角重构，结合自适应L1控制器提高了控制系统的稳定性。孙慧杰［103］针对运载火箭摆角输出受限或卡死的情况，采用L2增益干扰滑模控制器进行故障抑制，避免了控制饱和导致的箭体姿态不稳定。ZHAO等［104］考虑未知外部干扰、动力学建模误差、执行机构故障和执行机构约束的情况，通过输入输出反馈将运载火箭姿态动力学表述为二阶输入输出系统，使用广义比例积分（Generalized Proportional Integral，GPI）观测器对系统的状态和广义扰动进行估计，同时引入非线性积分滑模流形进行鲁棒容错滑模控制器设计，使该控制方案在面对执行机构故障和执行机构约束时具有良好的姿态跟踪性能。

3.4　震动抑制技术

由于测量得到的角度和角速度信号含有运载火箭的弹性震动和液体晃动信号，进而影响控制精度。如果运载火箭的弹性震动和液体晃动信号过大，将导致控制信号被覆盖，进而无法稳定箭体姿态，因此工程型号中通常采用陷波器抑制箭体弹性震动信号。如ORR等［90］通过线性滤波器实现太空发射系统横向弯曲和晃动的相位稳定。TROTTA等［95］为了增强对弹性模态参数变化的鲁棒性，为自适应增广控制集成了自适应陷波滤波器，以保证一阶弹性模态的相位稳定。LEFEVRE等［96］为避免箭体弹性震动信号影响姿态跟踪精度，在反馈控制回路中引入了滤波器，降低了弹性震动的影响。自适应滤波器的核心是震动频率辨识，主要有时域法和频域法［6］。时域法通过迭代或递归的方式来自适应更新陷波器参数，从而实现震动辨识，主要有阵列辨识法和模型辨识法等。但时域法运算量大、辨识参数精度不高。频域法通过傅里叶变换及插值方法将系统变换到频域内，然后采用极点配置自校正等方法进行陷波器设计。

1）时域法

范军朋［105］为辨识箭体弹性震动频率，基于递推最小二乘法设计了自适应陷波器。ZHAO等［104］为消除弹性模态的影响，采用自适应陷波器处理角度和角速度的量测信号。赵小平等［106］结合参数投影技术和μ综合法设计了自适应鲁棒∞控制器，以应对大型运载火箭飞行参数不确定性和弹性震动明显的情况。刘昆等［107］基于Steiglitz-McBride方法（SMM）设计了自适应滤波器抑制弹性震动信号。ZHANG等［99］基于SMM设计了自适应震动频率识别算法，并采用自适应IIR滤波器对火箭各阶震动频率进行识别，同时设计了相应的校正网络。张晋［108］设计了基于量子遗传算法的弹性震动抑制网络。

2）频域法

CHOI等［109］提出将陷波器极点保持在平面单位圆内并对参数进行自适应调整，可满足单参数滤波器始终稳定，保证滤波收敛，同时对弹性弯曲信号的抑制作用良好。KHOSHNOOD等［110］为解决箭体的震动滤波问题，基于模型参考自适应理论设计了陷波器，确保了姿态控制系统的闭环稳定。ELMELHI［111］采用径向基神经网络积分器替换了经典自适应陷波滤波器的频率跟踪积分器，从而扩大了经典自适应滤波器的跟踪范围，保证闭环系统在大频率弹性震动情况下仍能保持有效增益。CHOONG等［112］将运载火箭的平面运动简化为刚体俯仰运动与弹性震动耦合模型，通过自适应更新陷波器的参数，地面试验表明，该方法可以实现运载火箭的姿态稳定。张志健等［113］基于插值离散傅立叶变换设计了自适应陷波方法，以防止固定系数陷波器处理低频震动信号时导致的相位滞后问题。

3.5　控制技术小结

运载火箭动力系统故障主要是运载火箭推力下降和执行机构卡死，实现故障下的容错控制是运载火箭姿态控制的关键之一。随着运载火箭的大型化和复杂化，姿态控制系统的震动抑制能力也很重要。根据调研结果，自主故障诊断、控制力矩重构、陷波器3类技术的特征对比和总结分别如图4、表3和表4所示，而各类被动容错姿态控制方法在干扰、误差等不确定条件下的研究较为成熟，但对运载火箭动力系统故障的容错性能有待进一步研究。

图4　自主故障诊断方法性能对比

表3　控制力矩重构方法对比

表4　陷波器设计方法对比

4　人工智能技术的应用前景

航天事业的快速发展对运载火箭的安全性、可靠性和速度提出了新的要求，但传统的运载火箭制导控制技术需要大量的发射前准备工作，并且任务适应能力单一，难以适应未来复杂多变的发射任务和飞行工况。随着人工智能技术在控制领域的应用发展，采用人工智能技术解决传统制导控制技术难以克服的问题成为可能。目前，北京航天自动控制研究所提出了“会学习”的运载火箭概念，如图5所示，包括“边飞边学”和“终身学习”两大特征［114-115］。其中，“边飞边学”要求运载火箭充分利用箭上资源，在飞行过程中通过先进的控制理论和机器学习等技术实现飞行状态和环境参数在线辨识、运载和控制能力在线评估、目标在线变更、轨迹在线重新规划、控制力矩在线重构等功能，具备任务快响应、环境强适应、飞行自学习的特点。“终身学习”要求基于大数据等技术充分挖掘运载火箭全生命周期数据，完成智能建模、智能模型修正方案以及参数智能优化等工作，实现运载火箭制导控制系统的自我学习、优化更新和迁移推广。

图5　“会学习”的运载火箭概念

4.1　在自主制导方面的应用

人工智能方法在自主制导方面主要有2项应用：1）使用神经网络学习最优轨迹数据库，为任务目标轨道在线规划进行决策；2）采用基于强化学习等策略进行轨迹优化，但该方法的实时性有待提高。张荣升等［117］通过程序角优化构建了推力下降故障下运载火箭最优弹道数据库，并采用神经网络建立了推力下降故障与程序角之间的映射关系，使运载火箭在发生推力下降故障时能够在线估计剩余运载能力和重构程序角。HE等［34］采用由概率神经网络和基于故障救援知识训练的径向基函数神经网络组成的故障救援知识集成模型，来确定最优救援轨道。林子瑞等［3］针对运载火箭推力下降时无法正常入轨的问题，采用局部配点法建立推力下降故障下燃耗最优轨迹数据库，采用人工神经网络建立推力下降故障与入轨能力之间的映射关系，使运载火箭出现推力下降时实现入轨能力在线评估与决策，提高了发射任务的成功率。谭述君等［118］采用离线优化方法，建立各类故障下的“故障状态-救援轨道”样本集，采用径向基神经网络学习数据库得到入轨决策网络，并用于运载火箭在线轨迹重构。CELIS等［119］提出了基于神经网络的非线性混合算法，采用神经网络进行导航传感器数据融合以及动力学模型的学习。蒙特卡洛仿真表明，该方法在闭环制导中对发射任务、传感器性能、大气和推力偏差具有很高的鲁棒性。此外，国际制导控制专家IZZO等［120］阐述了人工智能方法在卫星控制、火箭垂直着陆、火箭制导等方面的应用和前景。CHENG等［121］和GAUDET等［122］分别采用深度神经网络和深度学习方法实现了小行星3自由度和6自由度着陆制导。陈书钊等［123］等提出了状态预测神经网络控制方法，完成了小型火箭垂直回收试验。

4.2　在故障诊断方面的应用

人工智能技术在运载火箭故障诊断领域应用较早，常用于地面测控系统对动力系统故障的监测、诊断和分析工作。例如，美国成熟的火箭发动机健康管理系统（Health Management System for Rocket Engine，HMSRE）中应用结构辨识神经网络，以及时间序列分析和长短时记忆神经网络［68］。在国内，李辉等［124-126］基于故障树和人工神经网络开发了运载火箭故障诊断软件，可实现发动机故障诊断和故障数据库更新。黄强等［127］开发了基于过程神经元网络、自适应神经模糊推理系统等技术的发动机地面试车故障检测和诊断系统。深度学习［128-129］、迁移学习［130-131］等网络也被用于发动机启动和稳态运行情况下的故障诊断和监管。但人工智能技术用于在线故障诊断的案例较少。YU等［132］为实现液体燃料火箭发动机的实时故障检测，提出了一种利用自适应遗传算法优化BP神经网络的实时故障诊断方法，将神经网络的预测值与实际收集的数据进行比较，并使用阈值判断机制确定发动机是否有故障，该算法具有较高的故障灵敏度和系统鲁棒性。XU等［133］采用量子遗传算法对BP神经网络参数进行优化，实现了液体燃料火箭发动机故障检测，在液体燃料火箭发动机典型故障检测仿真中，比传统BP神经网络和单一遗传算法的故障检测精度提高。

4.3　在容错控制方面的应用

容错控制方面，主要依赖各类新型神经网络开发具有干扰补偿和故障辨识能力的观测器，或者使用机器学习算法对现有容错控制律进行学习，设计具有故障自适应能力的容错控制器。CHEN等［134］针对运载火箭执行机构故障，研究了基于记忆增强神经网络（Memory-Augmented Neural Networks，MANN）的智能自适应容错控制，设计了二阶扰动观测器实现对时变扰动的精确估计和补偿，并引入MANN作为在线逼近器来抑制未知非线性的不利影响。同时，提出了自适应律来实现对执行机构故障的快速响应和MANN权值的更新。LI等［135］采用深度神经网络学习了推力下降故障下的伪逆分配数据，仿真表明，实际控制力矩能够很好地跟踪所需的控制力矩。SCLAFANI等［136］考虑建模不确定性、弹性动力学、燃油晃动和不稳定空气动力学等内外因素，结合忆递归神经网络和PID控制器提出了一种自适应控制策略，用于改善运载火箭的姿态控制品质。相比采用前馈神经网络和循环神经网络的PID控制器，该方法对控制系统不确定性和故障的容错能力更强。DUAN等［137］根据运载火箭姿态控制数据，采用无模型自适应控制（Model-Free Adaptive Control，MFAC）设计了运载火箭姿态控制律，对运载火箭载荷扰动有较好鲁棒性。黄旭等［138］建立了火箭频域分析和参数设计模型，采用双深度Q学习（Double Deep Q-Network，DDQN）算法，通过记忆回放和时间差分选代的方式，调整马尔可夫链模型来学习参数，最终得到的参数成功用于运载火箭姿控系统。

5　结束语

现役运载火箭的制导控制系统在建模时很少考虑动力系统非致命故障，并且算法对动力系统非致命故障的容错能力也有限，导致运载火箭难以适应推力下降和执行机构失效等动力系统故障。随着先进的控制理论的发展和人工智能技术的成熟，运载火箭应以软件为发展方导，研发具有自主决策和重构能力的智慧制导控制系统：

1）在制导方面，依托高性能箭机设备、最优化理论、人工智能等技术发展具备运载能力评估、任务目标规划和在线轨迹规划能力的自主制导算法，以弥补运载火箭飞行过程中地面指挥系统无法及时响应的缺点，增强运载火箭的自主能力。

2）基于先进的控制理论，提高现有主动、被动容错控制方法和震抑制方法的控制品质，并结合机器学习理论发展具有工程可行性的智能控制策略，保证故障下箭体姿态稳定。

3）利用数据挖掘技术，充分发掘现有大量地面测试和飞行数据的价值，通过自学习的方式从现有数据中提取新的故障诊断和制导控制策略，实现箭体软件系统升级换代。

［1］ 曲晶，张绿云.国外火箭发射及故障情况统计分析［J］.中国航天，2016（2）：13-18.

［2］ 刘秉.美国阿斯特拉太空公司AstraRocket3.3火箭发射故障分析［J］.中国航天，2021（9）：32-37.

［3］ 林子瑞，叶松，刘旭，等.运载火箭推力下降时入轨能力评估与轨迹重构方法［J］.吉林大学学报（工学版），2022（3）：1-12.

［4］ 常武权，张志国.运载火箭故障模式及制导自适应技术应用分析［J］.宇航学报，2019（3）：302-309.

［5］ ZHANG L， WEI C， LIANG J， et al. Heavy lift launch vehicle technology of adaptive augmented fault tolerant control［C］// 2016 IEEE Chinese Guidance， Navigation and Control Conference （CGNCC）. Washington D.C.， USA： IEEE Press， 2016： 1587-1593.

［6］ 张亮.重型运载火箭自适应控制方法研究［D］.哈尔滨：哈尔滨工业大学，2019.

［7］ 李学锋.运载火箭智慧控制系统技术研究［J］.宇航总体技术，2018，2（2）：43-48.

［8］ 宋征宇，吴义田，徐珊姝，等.长征八号：长征火箭系列商业化与智慧化的先行者［J］.深空探测学报（中英文），2021，8（1）：3-16.

［9］ 杨岫婷，苏磊，权赫，等.新一代大型运载火箭控制系统全数字动态重构技术［J］.导弹与航天运载技术，2021，7（5）：71-77.

［10］ 李平岐，李东，杨虎军，等.长征五号系列运载火箭研制应用分析及未来展望［J］.导弹与航天运载技术，2021，7（2）：5-8.

［11］ 宋征宇，潘豪，王聪，等.长征运载火箭飞行控制技术的发展［J］.宇航学报，2020，41（7）：868-879.

［12］ 宋征宇，巩庆海，王聪，等.长征运载火箭上升段的自主制导方法及其研究进展［J］.中国科学：信息科学，2021，51（10）：1587-1608.

［13］ LAWDEN D F. Optimal trajectories for space navigation［M］. Singapore： Butterworth & Co.Ltd.， 1963.

［14］ CHANDLER D C， SMITH I E. Development of the iterative guidance mode with its application to various vehicles and missions［J］. Journal of Spacecraft and Rockets， 1967， 4（7）： 898-903.

［15］ 王志祥.推力下降故障下运载火箭轨迹在线生成与姿控系统重构［D］.长沙：国防科学技术大学，2016.

［16］ CALISE A J， MELAMED N， LEE S. Design and evaluation of a three-dimensional optimal ascent guidance algorithm［J］. Journal of Guidance， Control， and Dynamics， 1998， 21（6）：867-875.

［17］ CALISE A J， BRANDT N. Generation of launch vehicle abort trajectories using a hybrid optimization method［J］. Journal of Guidance， Control， and Dynamics， 2004， 27（6）： 929-929.

［18］ GATH P F， CALISE A J. Optimization of launch vehicle ascent trajectories with path constraints and coast arcs［J］. Journal of Guidance， Control， and Dynamics， 2001， 24（2）：296-304.

［19］ DUKEMAN G A， CALISE A J. Enhancements to an atmospheric ascent guidance algorithm［C］// AIAA Guidance， Navigation， and Control Conference and Exhibit. Reston， USA： AIAA Press ， 2003： 1-11.

［20］ DUKEMAN G， HILL A. Rapid trajectory optimization for the Ares I launch vehicle［C］// AIAA Guidance， Navigation and Control Conference and Exhibit. Reston， USA： AIAA Press， 2008： 6288.

［21］ LU P， SUN H， TSAI B. Closed-loop endoatmospheric ascent guidance［J］. Journal of Guidance， Control， and Dynamics， 2003， 26（2）：283-294.

［22］ LU P， GRIFFIN B J， DUKEMAN G A， et al. Rapid optimal multiburn ascent planning and guidance［J］. Journal of Guidance， Control and Dynamic， 2008， 31（6）： 1656-1664

［23］ LU P， PAN B. Highly constrained optimal launch ascent guidance［J］. Journal of Guidance， Control， and Dynamics， 2010， 33（2）： 404-414.

［24］ HANSON J， SHRADER M W， CRUZEN C. Ascent guidance comparisons［C］// Guidance， Navigation， and Control Conference. Reston， USA： AIAA Press， 1995： 230-240.

［25］ 湛康意，陈海朋，贺从园，等.基于间接法在线能力评估和自主规划技术研究［J］.中国空间科学技术，2021，41（3）：31-38.

［26］ 李文清，王俊峰，张志国，等.火箭适应发动机推力下降故障的弹道制导策略优化分析［J］.导弹与航天运载技术，2020，6（4）：73-78.

［27］ 韩雪颖，马英，程兴，等.运载火箭推力故障下的弹道重构策略研究［J］.导弹与航天运载技术，2019，5（2）：7-11.

［28］ WANG C， SONG Z. Powered-coast-powered guidance reconfiguration method of launch vehicle with thrust drop fault［J］. Guidance， Navigation and Control， 2022， 2（1）： 2250003.

［29］ PATTERSON M A， RAO A V. GPOPS-Ⅱ： a Matlab software for solving multiple-phase optimal control problems using hp-adaptive Gaussian quadrature collocation methods and sparse nonlinear programming［J］. ACM Transactions on Mathematical Software （TOMS）， 2014， 41（1）： 1-37.

［30］ MA H，LI X，HUANG H. A trajectory re-planning method for multi-stage rockets based on decision classification［C］// Proceedings of the 38th Chinese Control Conference. Washington D.C.， USA： IEEE Press， 2019： 4119-4123.

［31］ LIU F， CHAO T， WANG S， et al. Trajectory optimization for launch vehicle boost phase based on gauss pseudospectral method［C］// 2016 35th Chinese Control Conference （CCC）. Washington D.C.， USA： IEEE Press， 2016： 10910-10914.

［32］ 马林.垂直起降运载火箭动力软着陆轨迹优化方法研究［D］.杭州：浙江大学，2019.

［33］ 张志国，余梦伦，耿光有，等.应用伪谱法的运载火箭在线制导方法研究［J］.宇航学报，2017，38（3）：262-269.

［34］ HE X， TAN S， WU Z， et al. Mission reconstruction for launch vehicles under thrust drop faults based on deep neural networks with asymmetric loss functions［J］. Aerospace Science and Technology， 2022， 121： 107375.

［35］ FAHROO F， ROSS I M. Pseudospectral methods for infinite-horizon nonlinear optimal control problems［J］. Journal of Guidance， Control， and Dynamics， 2008， 31（4）： 927-936.

［36］ YAN H， FAHROO F， ROSS I M. Optimal feedback control laws by Legendre pseudospectral approximations［C］// Proceedings of the 2001 American Control Conference. Washington D.C.， USA： IEEE Press， 2001： 2388-2393.

［37］ TIAN B， ZONG Q. Optimal guidance for reentry vehicles based on indirect Legendre pseudospectral method［J］. Acta Astronautica， 2011， 68： 1176-1184.

［38］ LIAO Y， LI H， BAO W. Indirect radau pseudospectral method for the receding horizon control problem［J］. Chinese Journal of Aeronautics， 2016， 29（1）： 215-227.

［39］ YANG L， ZHOU H， CHEN W. Application of linear gauss pseudospectral method in model predictive control［J］. Acta Astronautica， 2014， 96： 175-187.

［40］ RAHMAN T， ZHOU H， YANG L， et al. Pseudospectral model predictive control for exo-atmospheric guidance［J］. International Journal of Aeronautical and Space Sciences， 2015， 16（1）： 64-76.

［41］ MA Y， PAN B， TANG S. Improved parallel-structured Newton-type guidance for launch vehicles under thrust drop fault［J］. Journal of Spacecraft and Rockets， 2021，59（2）： 1-15.

［42］ ACIKMESE B， CASOLIVA J， CARSON J M， et al. G-fold： a real-time implementable fuel optimal large divert guidance algorithm for planetary pinpoint landing［J］. Concepts and Approaches for Mars Exploration， 2012， 1679： 4193.

［43］ CHENG X， LI H， ZHANG R. Efficient ascent trajectory optimization using convex models based on the Newton-kantorovich/pseudospectral approach［J］. Aerospace Science and Technology， 2017， 66： 140-151.

［44］ 王嘉炜，张冉，郝泽明，等.基于Proximal-Newton-Kantorovich凸规划的空天飞行器实时轨迹优化［J］.航空学报，2020，41（11）：116-125.

［45］ SUN Z， TAO C， WANG Y， et al. Convex method for ascent trajectory optimization using iterative narrowing trust region［C］// 2018 IEEE CSAA Guidance，Navigation and Control Conference （CGNCC）. Washington D.C.， USA： IEEE Press， 2018： 1-6.

［46］ ZHANG K， YANG S， XIONG F. Rapid ascent trajectory optimization for guided rockets via sequential convex programming［J］. Proceedings of the Institution of Mechanical Engineers， Part G： Journal of Aerospace Engineering， 2019， 233（13）： 4800-4809.

［47］ BENEDIKTER B， ZAVOLI A， COLASURDO G. A convex approach to rocket ascent trajectory optimization［C］// 8th European Conference for Aeronautics and Space Sciences . 2019：EUCASS2019-430.

［48］ BENEDIKTER B， ZAVOLI A， COLASURDO G， et al. Convex approach to three-dimensional launch vehicle ascent trajectory optimization［J］. Journal of Guidance， Control， and Dynamics， 2021， 44（2）：1-16.

［49］ 李敏，李惠峰，聂文明.火箭上升段滚动时域制导控制一体化设计［J］.宇航学报，2019（1）：41-50.

［50］ 王洪波，张若男，梁卓，等.基于改进序列凸优化的固体火箭入轨制导方法［J］.中国惯性技术学报，2021，29（1）：119-125.

［51］ 李师尧，常武权，闫宇申，等.运载火箭动力故障下的自主救援轨道规划［J］.飞行力学，2021，39（2）：83-89.

［52］ 宋征宇，王聪，巩庆海.运载火箭上升段推力下降故障的自主轨迹规划方法［J］.中国科学：信息科学，2019，49（11）：1472-1487.

［53］ LI Y， GUAN Y， WEI C， et al. Optimal control of ascent trajectory for launch vehicles： a convex approach［J］. IEEE Access， 2019（7）： 186491-186498.

［54］ LI Y， PANG B， WEI C， et al. Online trajectory optimization for power system fault of launch vehicles via convex programming［J］. Aerospace Science and Technology， 2020， 98： 105682.

［55］ MIAO X， SONG Y， ZHANG Z， et al. Successive convexification for ascent trajectory replanning of a multi-stage launch vehicle experiencing non-fatal dynamic faults［J］. IEEE Transactions on Aerospace and Electronic Systems， 2022，58（3）： 2039-2052.

［56］ SONG Z， WANG C， GONG Q. Joint dynamic optimization of the target orbit and flight trajectory of a launch vehicle based on state-triggered indices［J］. Acta Astronautica， 2020， 174： 82-93.

［57］ 罗亚中，唐国金，梁彦刚.基于分解策略的SSO发射轨道遗传全局优化设计［J］.航空学报，2004，25（5）：443-446.

［58］ 胡凡，杨希祥，江振宇，等.固体运载火箭轨迹/总体参数一体化优化设计研究［J］.固体火箭技术，2010，33（6）：599-602.

［59］ 杨希祥，李晓斌，肖飞，等.智能优化算法及其在飞行器优化设计领域的应用综述［J］.宇航学报，2009，30（6）：2051-2061.

［60］ 张柳，张雪梅，唐琼，等.基于组合粒子群算法的运载火箭弹道优化设计［J］.导弹与航天运载技术，2016（6）：1-5.

［61］ 高哲，王志刚.多约束条件下多级运载火箭弹道优化设计［J］.飞行力学，2018，36（6）：62-66.

［62］ 李晓苏.基于多目标智能算法的运载火箭上升段弹道优化设计［D］.哈尔滨：哈尔滨工业大学，2019.

［63］ ROSE M B， GELLER D. Linear covariance techniques for powered ascent［C］// AIAA Guidance， Navigation， and Control Conference. Reston， USA： AIAA Press， 2010： 8175.

［64］ 倪彧祺.考虑参数不确定性的运载火箭上升段参考轨迹优化［D］.哈尔滨：哈尔滨工业大学，2020.

［65］ SHEN H， SEYWALD H， POWELL R W. Desensitizing the minimum-fuel powered descent for Mars pinpoint landing［J］. Journal of Guidance， Control， and Dynamics， 2010， 33（1）： 108-115.

［66］ ZHANG D， LIU L， WANG Y. On-line ascent phase trajectory optimal guidance algorithm based on pseudo-spectral method and sensitivity updates［J］. The Journal of Navigation， 2015， 68（6）： 1056-1074.

［67］ 黄盘兴.重型运载火箭可重构控制系统设计研究［D］.哈尔滨：哈尔滨工业大学，2012.

［68］ 张振臻，陈晖，高玉闪，等.液体火箭发动机故障诊断技术综述［J］推进技术，2022，30（5）：40-45.

［69］ 宋征宇.运载火箭远程故障诊断技术综述［J］.宇航学报，2016，37（2）：135-144.

［70］ 叶松，陈曦，熊寸平.基于线性二次滚动时域法的运载火箭发动机推力故障诊断［J］.宇航总体技术，2020，4（6）：29-37.

［71］ 朱海洋，吴燕生，陈宇，等.适应运载火箭推力下降故障的神经网络容错控制方法［J］.航天控制，2019，37（4）：3-9.

［72］ 朱海洋，吴燕生，容易，等.适应有限故障的运载火箭神经网络自适应容错控制［J］.西北工业大学学报，2020，38（3）：668-676.

［73］ 符文星，朱苏朋，阎杰，等.参数估计法在运载火箭动力系统故障诊断中的应用［J］.弹箭与制导学报，2007，27（1）：181-183.

［74］ ZHANG T， ZHAO X， HU R， et al. A method for fault diagnosis of power system of carrier rocket engine based on linear-quadratic receding time-domain algorithm［J］. Proceedings of the Institution of Mechanical Engineers， Part G： Journal of Aerospace Engineering， 2021： 09544100211021805.

［75］ CHEN H， YAN J， ZHANG T， et al. On-line fault diagnosis of launch vehicle thrust loss based on parameter estimation method［C］// 2021 IEEE Asia-Pacific Conference on Image Processing， Electronics and Computers （IPEC）. Washington D.C.， USA： IEEE Press，2021： 871-876.

［76］ CHA J， KO S， PARK S Y， et al. Fault detection and diagnosis algorithms for transient state of an open-cycle liquid rocket engine using nonlinear Kalman filter methods［J］. Acta Astronautica， 2019， 163：147-156.

［77］ LEE K， CHA J， KO S， et al. Fault detection and diagnosis algorithms for an open-cycle liquid propellant rocket engine using the Kalman filter and fault factor methods［J］. Acta Astronautica， 2018， 150： 15-27.

［78］ 闫晓东，孙成志.基于神经网络和证据理论的火箭发动机故障诊断方法［J］.宇航总体技术，2020，4（4）：20-30.

［79］ 王硕，潘豪，白文艳，等.基于惯组信息的运载火箭主发动机推力故障在线辨识［J］.航天控制，2019，37（6）：8-12.

［80］ 赵万里，郭迎清，杨菁，等.液体火箭发动机故障诊断器设计及其HIL验证［J］.北京航空航天大学学报，2019，45（10）：1995-2002.

［81］ 孟洲.发动机执行机构故障下大型捆绑火箭容错控制［D］.长沙：国防科学技术大学，2013.

［82］ 尹彪，刘磊，王永骥.火箭姿态控制与故障重构的研究［C］//中国自动化学会中南六省区自动化学会学术年会.2010：245-249.

［83］ 李铸.运载火箭推力下降故障下姿态容错控制［D］.武汉：华中科技大学，2020.

［84］ 冯昊，李新明，潘豪.大推力运载火箭控制系统控制力重构技术研究［J］.载人航天，2012，18（6）：75-79.

［85］ 程堂明，李家文，唐国金.执行机构故障下基于线性规划的运载火箭姿控系统重构控制［J］.国防科技大学学报，2017，39（1）：51-57.

［86］ 余光学，宋敬群，杨华.运载器姿态控制重构研究［J］.导弹与航天运载技术，2021，7（1）：61-67.

［87］ ZHANG Y， LI Z， CHENG Z， et al. Attitude tracking control reconfiguration for space launch vehicle with thrust loss fault［J］. IEEE Access， 2019（7）： 184353-184364.

［88］ 于海森，谭述君，吴志刚.基于Armijo准则和BFGS算法的运载火箭控制重分配［J］.航空动力学报，2022，37（1）：204-213.

［89］ WEI C， WANG M， LU B， et al. Accelerated Landweber iteration based control allocation for fault tolerant control of reusable launch vehicle［J］. Chinese Journal of Aeronautics， 2022， 35（2）： 175-184.

［90］ ORR J， VAN Z T. Robust， practical adaptive control for launch vehicles［C］// AIAA Guidance， Navigation， and Control Conference. Reston， USA： AIAA Press， 2012： 2012-4549.

［91］ LEFEVRE B， JHA R. Launch vehicle ascent flight control augmentation via a hybrid adaptive controller［C］// AIAA Guidance， Navigation and Control Conference and Exhibit. Reston， USA： AIAA Press 2008： 7130.

［92］ HANSON C E， MILLER C J， VANZWIETEN T S， et al. Launch vehicle manual steering with adaptive augmenting control： in-flight evaluations of adverse interactions using a piloted aircraft ［C］// AIAA Guidance， Navigation， and Control Conference. Reston， USA： AIAA Press， 2015： 1776.

［93］ 吴蕾.考虑发动机推力损失的运载火箭容错控制［D］.大连：大连理工大学，2019.

［94］ 何飞毅.重型运载火箭模型参考自适应增广控制研究［D］.哈尔滨：哈尔滨工业大学，2018.

［95］ TROTTA D， ZAVOLI A， DE MATTEIS G， et al. Optimal tuning of adaptive augmenting controller for launch vehicles in atmospheric flight［J］. Journal of Guidance， Control， and Dynamics， 2020， 43（11）： 2133-2140.

［96］ LEFEVRE B D， JHA R. Hybrid adaptive ascent flight control for a flexible launch vehicle［J］. Proceedings of the Institution of Mechanical Engineers， Part G： Journal of Aerospace Engineering， 2011， 225（8）： 851-862.

［97］ 崔乃刚，陈诚，潘哲，等.运载火箭自适应增广抗扰减载控制［J］.导弹与航天运载技术，2017，3（6）：1-7.

［98］ 梁小辉，胡昌华，周志杰，等.基于自适应动态规划的运载火箭智能姿态容错控制［J］.航空学报，2021，42（4）：511-524.

［99］ HANG L， WEI C， WU R， et al. Fixed-time extended state observer based non-singular fast terminal sliding mode control for a VTVL reusable launch vehicle［J］. Aerospace Science and Technology， 2018， 82： 70-79.

［100］马艳如，王青，胡昌华，等.执行器故障下的运载火箭非奇异终端滑模容错控制［J］.宇航学报，2020，41（12）：1553-1560.

［101］马艳如，石晓荣，刘华华，等.运载火箭姿态系统自适应神经网络容错控制［J］.宇航学报，2021，42（10）：1237-1245.

［102］苏秀健.基于L1自适应方法的火箭姿态控制［D］.大连：连理工大学，2020.

［103］孙慧杰.火箭起飞段姿态系统的滑模变结构控制［D］.哈尔滨：哈尔滨工业大学，2013.

［104］ZHAO D J， WANG Y J， LIU L， et al. Robust fault‐tolerant control of launch vehicle via GPI observer and integral sliding mode control［J］. Asian Journal of Control， 2013， 15（2）： 614-623.

［105］范军朋.考虑不确定性的火箭姿态自适应控制系统设计［D］.大连：大连理工大学，2013.

［106］赵小平.基于自适应H∞的重型运载火箭u姿态控制方法研究［D］.哈尔滨：哈尔滨工业大学，2012.

［107］刘昆，孙平.固体运载器姿态控制系统自适应滤波器设计［J］.国防科技大学学报，2010，32（5）：44-48.

［108］张晋.固体运载器自适应增广抗扰姿态控制方法研究［D］.哈尔滨：哈尔滨工业大学，2020.

［109］CHOI H D， BANG H. An adaptive control approach to the attitude control of a flexible rocket［J］. Control Engineering Practice， 2008（8）： 1003-1010.

［110］KHOSHNOOD A M， ROSHANIAN J. Model reference adaptive control for a flexible launch vehicle［J］. Proceedings of the Institution of Mechanical Engineers Part Ⅰ Journal of Systems and Control Engineering， 2008， 222（1）： 49-55.

［111］ELMELHI A. Modified adaptive notch filter based on neural network for flexible dynamic control［J］. International Journal of Computer and Electrical Engineering， 2014， 6（2）： 185-190.

［112］CHOONG S， BANG H， PARK C S. Attitude control of a flexible launch vehicle using an adaptive notch filter： ground experiment［J］. Control Engineering Practice， 2008， 16（1）： 30-42.

［113］张志健，王小虎.固体火箭多约束耗尽关机的动态逆能量管理方法［J］.固体火箭技术，2014，37（4）：435-441.

［114］马卫华，禹春梅，路坤锋，等.“会学习”运载火箭的制导控制技术［J］.航天控制，2020，38（2）：3-8.

［115］包为民.航天智能控制技术让运载火箭“会学习”［J］.航空学报，2021，42（11）：8-17.

［116］张惠平，路坤锋，曹玉腾.人工智能技术在“会学习”运载火箭的应用现状和发展展望［J］.中国航天，2021（2）：9-13.

［117］张荣升，吴燕生，秦旭东，等.运载火箭推力下降故障下的在线弹道重构方法［J］.南京航空航天大学学报，2021，53（1）：25-37.

［118］谭述君，何骁，张立勇，等.运载火箭推力故障下基于智能决策的在线轨迹重规划方法［J］.宇航学报，2021，42（10）：1228-1236.

［119］CELIS D R， LOPEZ P S， CADARSO L. Sensor hybridization using neural networks for rocket terminal guidance［J］. Aerospace Science and Technology， 2021， 111： 106527.

［120］IZZO D， MARTENS M， PAN B. A survey on artificial intelligence trends in spacecraft guidance dynamics and control［J］. Astrodynamics， 2019， 3（4）： 287-299.

［121］CHENG L， WANG Z， SONG Y， et al. Real-time optimal control for irregular asteroid landings using deep neural networks［J］. Acta Astronautica， 2020， 170： 66-79.

［122］GAUDET B， LINARES R， FURFARO R. Deep reinforcement learning for six degree-of-freedom planetary landing［J］. Advances in Space Research， 2020， 65（7）： 1723-1741.

［123］陈书钊，楚龙飞，杨秀梅，等.状态预测神经网络控制应用于小型可回收火箭［J］.航空学报，2019，40（3）：154-168.

［124］刘小明，李辉，蒋吉兵.基于故障树和神经网络的火箭故障诊断方法［J］.计算机仿真，2010，27（7）：38-42.

［125］郭博.基于神经网络和故障树的运载火箭故障诊断系统的研究［D］.成都：电子科技大学，2010.

［126］尹茂君.运载火箭故障诊断系统研究与实现［D］.成都：电子科技大学，2011.

［127］黄强，吴建军.基于云-神经网络的液体火箭发动机故障检测方法［J］.国防科技大学学报，2010，32（1）：11-15.

［128］PARK S Y， AHN J. Deep neural network approach for fault detection and diagnosis during startup transient of liquid-propellant rocket engine［J］. Acta Astronautica， 2020， 177： 714-730.

［129］LI H， DENG Z， ZHANG J， et al. A deep learning based fault detection method for rocket launcher electrical system［C］// International Conference on Machine Learning， Optimization， and Data Science. Berlin， Germany： Springer， 2020： 316-325.

［130］张晨曦，唐曙，唐珂.迁移学习下的火箭发动机参数异常检测策略［J］.计算机应用，2020，40（9）：2774-2780.

［131］LV H， CHEN J， WANG J， et al. A supervised framework for recognition of liquid rocket engine health state under steady-state process without fault samples［J］. IEEE Transactions on Instrumentation and Measurement， 2021， 70： 1-10.

［132］YU H， WANG T. A method for real-time fault detection of liquid rocket engine based on adaptive genetic algorithm optimizing back propagation neural network［J］. Sensors， 2021， 21（15）： 5026.

［133］XU L，ZHAO S， LI N， et al. Application of QGA-BP for fault detection of liquid rocket engines［J］. IEEE Transactions on Aerospace and Electronic Systems， 2019， 55（5）： 2464-2472.

［134］CHEN H， CHEN K， FU W. Memory augmented neural network-based intelligent adaptive fault tolerant control for a class of launch vehicles using second-order disturbance observer［J］. Mathematical Problems in Engineering， 2021： 9961278.

［135］LI Z， ZHANG Y， LIANG Z， et al. Control allocation reconstruction of launch vehicle based on neural network［C］// Proceedings of the 11th International Conference on Modelling， Identification and Control （ICMIC2019）. Berlin， Germany： Springer， 2020： 1025-1033.

［136］SCLAFANI R， SHANKAR P. Variable memory recurrent neural networks for launch vehicle attitude control［C］// AIAA Guidance， Navigation， and Control Conference. Reston， USA： AIAA Press， 2015： 1774.

［137］DUAN L， HOU Z， YU X， et al. Data-driven model-free adaptive attitude control approach for launch vehicle with virtual reference feedback parameters tuning method［J］. IEEE Access， 2019（7）： 54106-54116.

［138］黄旭，柳嘉润，骆无意.基于DDQN的运载火箭姿态控制器参数设计［J］.航天控制，2020，38（4）：3-8.

Overview of Guidance and Control Technologies for Launch Vehicles under Propulsion System Faults

LIShuang1， LIUXu1， YESong2， LINZirui1

（1.College of Astronautics， Nanjing University of Aeronautics and Astronautics， Nanjing 211106， Jiangsu， China； 2.Beijing Aerospace Automatic Control Institute， Beijing 100854， China）

Propulsion system faults are the most common causes for launch vehicle failure. In this paper， the guidance and control technologies for launch vehicles under propulsion system faults are overviewed from the aspects of fault modeling， autonomous guidance， and fault-tolerant control， which may enlighten the development of new guidance and control algorithms. First， the mathematical modeling of thrust drop and actuator faults is established， and the guidance and control performance of advanced launch vehicles at home and abroad is compared. Second， the trajectory optimization and guidance algorithms involved in autonomous guidance under faults are summarized. Third， the typical fault diagnosis， control reconstruction， fault-tolerant control， and vibration suppression methods within the framework of passive and active fault-tolerant control are reviewed. Meanwhile， the application of artificial intelligence technologies to fault diagnosis and guidance control is summarized. Finally， with the introduction of the “learning” launch vehicle concept， the development trend of artificial intelligence technologies in improving the autonomy and intelligence of launch vehicles is discussed， and the guidance and control technologies for future intelligent launch vehicles are envisaged.

launch vehicle； propulsion system fault； fault diagnosis； guidance and control； artificial intelligence

2022‑03‑25；

2022‑06‑06

国家自然科学基金项目（61273051，11672126）；航天一院高校联合创新基金（CALT201703）

李爽（1978—），男，博士，教授，主要研究方向为航天器动力学与控制、深空探测技术、空间态势感知与博弈。

V 448.1

A

10.19328/j.cnki.2096⁃8655.2022.04.008