一种基于固定正确率的GNSS模糊度差值检验阈值确定方法
薛红琳 王家福 于先文
0 引言
全球导航卫星系统(Global Navigation Satellite System,GNSS)因其全天候、高精度的优点,被广泛应用于自然保护地监管、地质矿产、国土空间规划等领域[1-3].载波相位定位技术是GNSS精密定位最常用的方法.然而在载波相位测量过程中,始终存在着一个整周未知数,该整周未知数常被称作整周模糊度.准确快速地确定整周模糊度是实现GNSS载波精密定位的必要条件和关键问题.
当前,整周模糊度的解算普遍按照4个步骤进行[4]:第1步,根据平差模型解算出模糊度及其他参数的实数解;第2步,对模糊度的实数解进行整数估计,得到模糊度的候选整数解;第3步,对模糊度的候选整数解进行确认;第4步,一旦候选整数解通过确认,便将其作为模糊度真值进行回代从而修正定位解.然而,由于载波相位观测过程中存在着各种误差,所求得的模糊度候选解不一定是正确的,因此在得到模糊度的候选整数解之后,对其进行检验确认的步骤就显得尤为重要.
早期的模糊度检验方法主要是通过判断最优候选解与次优候选解之间是否存在显著差异来判断最优候选解能否通过检验的.这类区别性检验方法主要包括F-ratio Test[5]、R-ratio Test[6]、W-ratio Test[7]和差值检验(Difference Test)[8]等.差值检验是上述模糊度检验方法中最常用的方法之一,它利用最优候选解与次优候选解对应的残差二次型进行求差,用这个差值表示最优解与次优解之间的差异程度,并与给定的阈值相比较,以此来判断最优解是否能通过检验.在差值检验的过程中,一个关键的步骤是给定阈值.通常,差值检验的阈值主要是根据经验给定固定值[6,9],这种方法简单但可靠性难保障.整数孔径估计理论提出后,Teunissen[10-11]提出一种基于固定失败率的阈值确定方法.这种方法将阈值与失败率联系起来,给出了一种建立表格的方法,根据用户需要的失败率水平来确定对应的阈值[12-13].随后,吴泽民等[14-15]提出了后验概率检验,从贝叶斯理论入手深入研究了相应的模糊度固定方法.对于应用颇为广泛的固定失败率方法来说,虽然该方法能通过控制孔径大小来控制失败率水平,但是缺陷与经验法类似,所得阈值不能直观地反映定位解的正确程度.
本文首先对整数孔径估计理论和固定正确率进行分析,在此基础上提出一种基于固定正确率的差值检验阈值确定方法,并根据半仿真计算给出了相应的阈值取值建议.
1 整数孔径估计
1.1 基本理论
任何GNSS载波定位模型都可以用下式表示:
V=Aa+Bb-L,
(1)
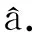
Ua∩Ub=∅,∀a,b∈Zn,a≠b,
Uz=U0+z,∀z∈Zn,
(2)
式中,Uz表示整数孔径估计的归整域,U表示整数孔径估计的全体归整域集合,U0表示原始归整域,z表示整数平移向量.
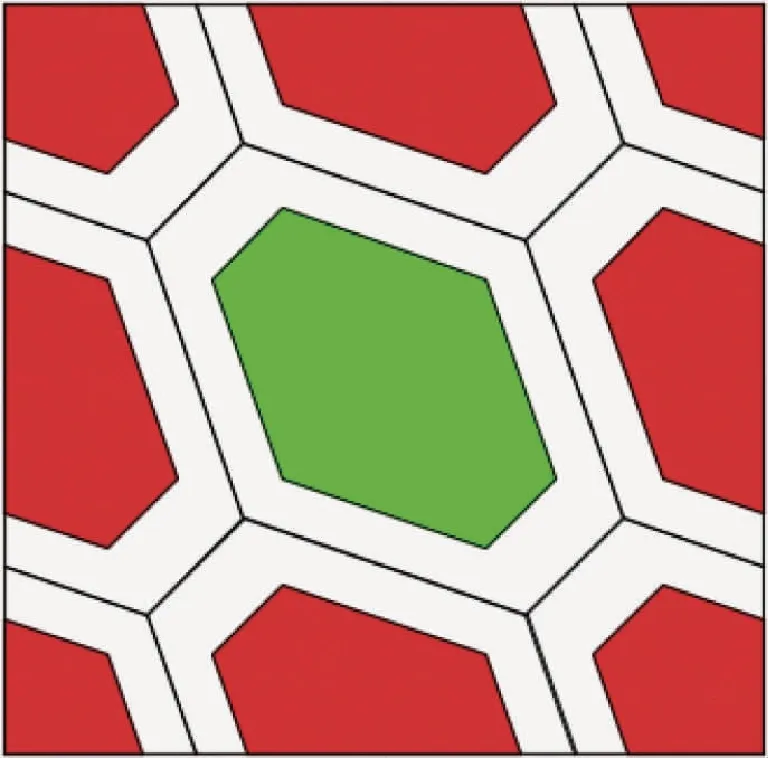
图1 二维情况整数孔径估计的归整域(绿色:固定正确;红色:固定错误;白色:无法固定)Fig.1 Pull-in regions of integer aperture estimation for 2-dimensional case(green:fixed correctly;red:fixed incorrectly;white:could not be fixed)
图1表示二维情况下整数孔径估计的归整域.由整数孔径估计的定义可知模糊度估计对应着3种结果,即成功、失败以及无法固定.
1)模糊度实数解落入正确的归整域Ωs,如图1中绿色区域,此时模糊度固定成功;
2)模糊度实数解落入错误的归整域Ωf,如图1中红色区域,此时模糊度固定失败;
3)模糊度实数解并未落入任一归整域而是落入了不确定域,如图1中白色区域,此时模糊度无法固定为整数,只能采用实数解.
相应地,模糊度估计的3种不同结果分别对应着成功率Ps、失败率Pf以及不确定率Pu:
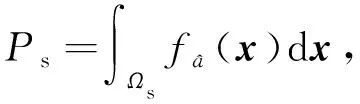
(3)
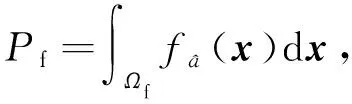
(4)

(5)
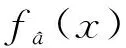
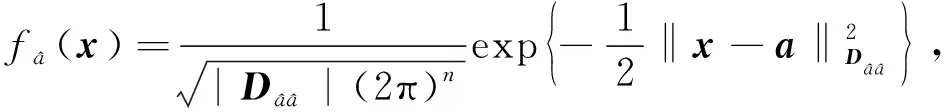
(6)
1.2 固定正确率
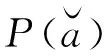
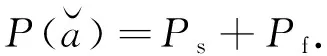
(7)
在此基础上,最优整数解是模糊度真值的概率表示为
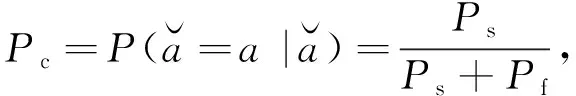
(8)
式中的Pc即为固定正确率.
2 基于固定正确率的阈值确定方法
针对经验法缺乏理论基础和固定失败率方法不能反映模糊度估值正确程度的问题,本文提出了一种基于固定正确率来确定差值检验阈值的方法.
2.1 差值检验的概念
差值检验对最优整数解与次优整数解的残差二次型之间的差异程度进行判断.差值检验定义为
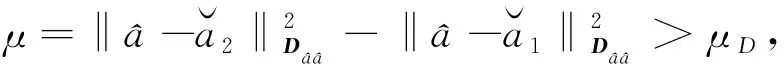
(9)
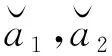
2.2 阈值确定策略
基于固定正确率阈值确定方法的具体步骤如下:
1)对于一个特定GNSS模型,解算得到所有历元的实数解及其方差矩阵.
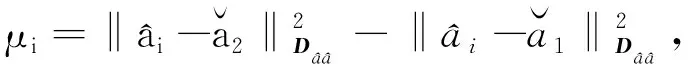
4)将最小值umin作为阈值,统计模糊度固定正确的组数Ns和模糊度固定错误的组数Nf,计算阈值umin对应的固定正确率Pc(umin)=Ns/(Ns+Nf).如果此时固定正确率低于85%,则认为此历元精度太低而不适合固定,转从下一历元开始进行;如果高于85%,则继续进行以下步骤.
5)在[umin,umax]区间内改变阈值的取值,计算不同阈值对应的固定正确率,得到众多以阈值为横坐标、以正确率为纵坐标的点对数据(ui,PC,i)(i=1,2,…).
6)通过改变测站、改变卫星数目,或者说改变模糊度的维数来产生不同观测环境下的定位模型,然后重复以上的步骤,便能得到不同定位模型下的点对数据(ui,PC,i)(i=1,2,…).
7)拟合散点数据,得到相应函数图形.根据需要的固定正确率水平和模糊度维数,即可通过拟合得到的函数图形来确定满足用户要求的阈值.
2.3 半仿真计算
按照2.2节的具体步骤,本文设计了一个半仿真实验来确定差值检验的阈值.为了避免系统误差的影响,本节采用多组短基线数据进行计算,所用数据来自澳大利亚科廷大学的CORS基站和南京市东南大学校内GNSS基站.
利用软件进行解算,得到测试数据所有历元的实数解及其方差矩阵.然后按照2.2节中的相应步骤,得到了模糊度维数(n)从3维到9维的情况下,差值检验阈值与固定正确率之间的拟合函数图形.由于篇幅有限,本文给出了部分拟合结果如图2和图3所示.

图2 6维模糊度拟合情况Fig.2 Fitting of 6-dimensional ambiguity
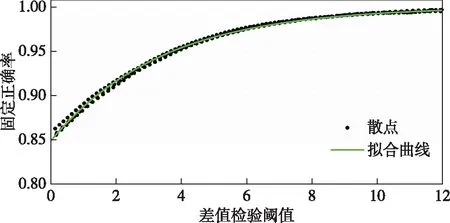
图3 9维模糊度拟合情况Fig.3 Fitting of 9-dimensional ambiguity
拟合函数选用指数函数,图2和图3对应的拟合精度如表1所示.
表1中:RMSE代表拟合标准差,单位同正确率保持一致,描述的是拟合的正确率与原正确率之间的离散程度;R-square代表拟合优度,取值为[0,1],越接近于1代表该模型对原数据拟合得越好.由表1可见,图2和图3中的拟合曲线能较好地拟合原散点数据.

表1 6维和9维模糊度拟合精度
2.4 阈值取值建议
2.3节得到了3维~9维模糊度的情况下差值检验阈值与固定正确率之间的拟合图形,由此便建立差值检验阈值与固定正确率之间对应的关系,进一步可以根据固定正确率来确定阈值.
下面给出95%和99%两种正确率水平下差值检验的阈值表,如表2所示.
由表2可见:当保持固定正确率一定时,模糊度维数越高,相应的阈值应该选择得越小;当模糊度维数一定时,选择更大的阈值就能保证更大的固定正确率,从而获得更可靠的定位结果.在实际定位中,使用者可以根据工程所需要的定位解可靠性水平以及当前卫星的数量,选择对应的差值检验阈值.

表2 95%和99%的固定正确率水平下模糊度维数与阈值对应表
3 结论与展望
针对经验法缺乏理论基础和固定失败率方法不能直观反映模糊度估值正确程度的问题,本文在对整数孔径估计理论和固定正确率进行分析的基础上,提出了一种基于固定正确率的GNSS模糊度差值检验阈值确定方法,并利用半物理仿真实验给出了相应的阈值取值建议.该方法既能保证模糊度固定之后的正确水平,同时又能根据不同的模糊度维数来确定对应的阈值.
在以后的研究中,可以结合工程项目对该方法的实际表现进一步进行深入分析.

