基于STEAM理念的高等数学课堂教学模式探究——以牛顿—莱布尼茨公式为例

王湘萍

（贵州师范大学数学科学学院，贵州贵阳 550001）

1 STEAM教育及特点

STEAM教育源自20世纪80年代美国人提出的STEM教育，是当今国际社会探索21世纪人才培养的一种教育理念与参照。STEAM教育重视数学、科学、技术、工程、艺术等学科的相互融合，突出培养学生的动手能力和跨学科思维能力，建构了文、理、术等多学科融合的完整知识体系。

STEAM教育的主要特点是通过项目问题情境、创新成果导向等核心教学活动，培养学生设计与解决问题能力、沟通和表达能力以及创新应用能力 ，促进学生跨学科思维能力的发展，培养学生的数学核心素养。

2 现行高等数学课堂教学模式存在的问题

目前，大部分高等数学课堂采用的是传统的教学模式——黑板+PPT课件，利用教育新技术、新教学手段和方法的较少。现行高等数学课堂教学模式主要存在以下几个问题：

（1）近年来，由于高等教育的不断改革，招生规模不断扩大，高考时的录取分数为总体分数，这使得同一专业的学生数学基础参差不齐，再加上高等数学是公共必修基础课，相对于高中数学来说，高等数学概念多、抽象，部分学生在学习过程中积极性不高。

（2）课堂教学模式单一，学生听课状态不佳，学习参与度不高。

（3）教材内容相对陈旧，教学体系单一，学生的学习兴趣不高 。再加上教学计划和大纲过于陈旧，无法有效帮助学生掌握数学思想、数学方法和学习新知识。

（4）大班教学影响教学效果。大部分班级人数过多，少则七八十人，多则上百人。教师在上课时不能兼顾所有学生，项目化教学、案例教学、翻转课堂等教学模式开展不起来。

（5）教学手段单一，缺乏现代教育技术的有效整合。其一，所用教室虽装有多媒体，但只可以使用教学课件，不可上网，没能真正实现网络化、信息化；其二，部分教师使用现代教育技术的能力有所欠缺，即使使用现代教育技术进行教学，也仅是把它代替黑板，没有让现代教育技术在高等数学教学中真正发挥作用。

3 基于STEAM理念的高等数学课堂教学路径设计

课堂教学是教师传授知识的主要阵地，是培养学生能力的重要方式。高等数学课堂教学要注重调动学生学习兴趣，培养学生创新能力，全面提高高等数学的教学质量。为此，基于对STEAM教育理念的初步探讨，结合当前高校高等数学课堂教学的现状，以牛顿—莱布尼茨公式为例，设计出高等数学课堂教学新路径。

3.1 创设有效情境，提出问题，激发学生学习兴趣

在教授牛顿—莱布尼茨公式时，可这样创设有效情境：由定积分定义求时要经过分割、近似、求和、取极限四个步骤，计算过程冗长而繁杂。可先提出问题：能不能找到一种有效、直接的工具来计算定积分？牛顿—莱布尼茨公式就是这样一种工具。学生在高中已经初步接触过这个公式，但只是会用，而不知道是怎样得出来的，为什么要以两个数学家的名字来命名，通过设问将定积分计算与历史上著名的科学家等联系起来，激发学生的求知欲。

3.2 重点讲授，唤起记忆，增加知识的关联

通过对主要知识点的讲解来唤醒学生记忆中已有的知识，并与所学知识联系起来，形成跨学科思维。在讲解牛顿—莱布尼茨公式时，重点讲授公式的证明过程，让学生理解积分上限函数的性质和原函数存在定理，把求一个连续函数在区间上的定积分的值与找这个连续函数的一个原函数联系起来，并了解微积分基本定理是联系积分学与微分学之间的桥梁。

3.3 基于项目驱动、案例分析，提高主动性

通过对具体案例进行分析，引导学生进行交流探讨，鼓励学生在探索中应用过程性技能，如观察、提问和讨论等，建立起学科之间的联系，去思考解决实际问题。例如，对牛顿—莱布尼茨公式的证明探讨完后，可以安排三个例题。例题的安排遵循由简到难、从单一到综合的规律，鼓励学生根据题目本身特点动手画出平面图形，在解题上以问答和分组讨论的形式进行。例1较为简单，利用定积分的性质即可。

例2、例3都是求分段函数的定积分，这是一个难点。由于牛顿—莱布尼茨公式的前提是被积函数是连续函数，如果不是连续函数或有有限个间断点，该怎样求得？引导学生分析，发现在各个积分区间，被积函数都是连续函数，可以利用定积分对积分区间具有可加性的性质求得。将原式中积分区间[0,2]分成两个积分区间[0，1]，[1，2],求出定积分的值，再相加即可。于是，对分段函数求定积分，可以分段积分，再相加。

解：∵函数在[0，2]上不连续，但是分段连续

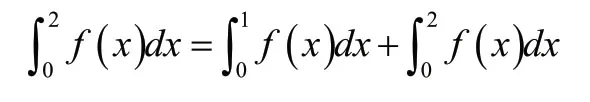
在[1,2]上规定当x=1时，f(x)=5，

解：由图形可知

则，原式=

3.4 教学反思，提炼升华

课堂教学最后由教师和学生对整个教学过程和教学结果讲行评价反思，推进课程教学近一步提升。在对牛顿—莱布尼茨公式证明结束时进行升华反思[7]，引导学生思考证明中用到了什么定理？哪些知识点？找到微分与积分之间的关系，总结出微积分基本定理不仅是沟通微分学和积分学之间的桥梁，而且还充分体现了数学之美——对称美（见图1）。

图1 数学之美——对称美

4 基于STEAM理念的高等数学课堂教学路径实施策略

（1）深挖课程思政。将数学历史、数学概念、数学故事以及数学知识点在现实中的应用作为切入点 ，深挖课程思政，促使STEAM理念在高等数学课堂落地生根。在讲授教学牛顿—莱布尼茨公式之前，由历史故事：17世纪数学史上著名公案“牛顿与莱布尼茨微积分创始人之争”引入新课，介绍牛顿、莱布尼茨两位数学家对微积分创始的贡献，引导学生不仅领略数学文化遗产的魅力，扩展知识领域，又提升人文素养。

（2）注重多学科的交叉融合。STEAM教育最突出的特点就是跨学科性。教师教学设计应注意课程横向和纵向的融合 ，建立起多学科之间的联系，培养学生的跨学科、跨区域思维能力。

讲授牛顿—莱布尼茨公式的应用时，强调它不仅可以求多个函数的和与差在区间[a,b]上的定积分的值，如例1，还可以用来求曲线弧的长度、曲线围成的平面图形的面积和立体的体积等横向问题，同时在变力做功、水压力、引力等纵向问题的应用也较为广泛。

例4 一物体按规律x=ct3做直线运动，介质的阻力与速度的平方成正比。计算物体由x=0移到x=a时，克服介质阻力所做的功[10]。

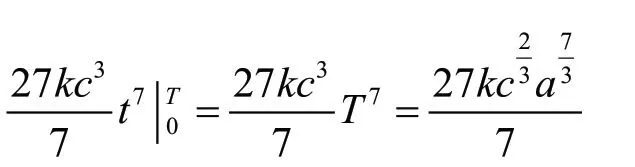
（3）使用多样化的教学手段。随着“互联网+”“大数据”时代的到来，高等数学课堂教学的方法、手段也要随之改变。

在新课引入时，可以应用动画制作技术，将牛顿、莱布尼茨的画像展示给学生；在知识回顾和讲解公式的应用时，可以把传统教学手段与现代化教学手段相结合，即板书与多媒体课件相结合，激发学生学习的兴趣，创新课堂教学模式，提升课堂教学效果。

（4）采用案例、项目驱动教学。以问题为驱动的教学模式是STEAM教育最常用的教学模式。课堂上采用案例分析或项目驱动的方式，围绕一个具体问题进行分析，找到解决问题的方法，践行“以学生为中心”的理念。

例如，探究牛顿—莱布尼茨公式的证明过程。

定理：如果函数F(x)是连续函数f(x)在区间[a，b]上的一个原函数，那么dx=F(b)-F(a)[12]。

首先对公式进行分析，在精确掌握公式内涵的基础上，找出已知条件，即F(x)是f(x)的一个原函数，这显然是不够的，怎么办？能否从学过的定理和性质中找到第二个条件？引导学生记忆积分上限的函数和原函数的存在定理，即，连续函数在定义区间内必有原函数存在，而且原函数的形式以积分上限函数Φ(x)=的形式给出，这样就找到了连续函数f(x)的两个原函数：F(x)、Φ(x)=，由原函数的定义知道，这两个原函数之间相差一个常数C，即F(x)-Φ(x)=C(a≤x≤b)，就找到了证明的突破口。

（5）转变教育观念，提高教学水平。随着大数据、“互联网+”的飞速发展，迫切需要提高教师教学水平。高校教师不但在教学方法、手段上不断创新，而且在教学模式、教学理念上要进行创新和转变，打造“金课”，淘汰“水课” ，提升教学质量。在高等数学课堂上引入STEAM教育理念，教师要根据数学学科与信息、工程、技术、艺术等科目各自的特点，寻求它们之间可以融合的突破口，同时关注本学科的前沿知识，及时更新自己的相关知识，进一步提高课堂教学质量，培养学生的数学核心素养[13]。

5 结语

STEAM教育作为一种新兴的教育理念，要想在高等数学课堂教学中落地生根，需社会、学校、教师和学生相互配合、共同努力。既要以学生为中心，注重学生的全面发展，又要转变观念，改革教学方法和手段，提高教学质量[14]。