分块矩阵Drazin逆的简单结果

杨晓英，王亚强，刘 新

(1.四川信息职业技术学院 人文学院，四川 广元 628017；2.宝鸡文理学院 数学与信息科学学院，陕西 宝鸡 721013)

设Cm×n表示m×n阶复矩阵的集合，A∈Cn×n，若X∈Cn×n满足下列方程[1]：

(i)Ak+1X=Ak, (ii)XAX=X, (iii)AX=XA,

则称X为A的Drazin逆，记作X=AD，称k为A的指数，记作ind(A)=k，记Aπ=I-AAD。矩阵的Drazin逆是矩阵广义逆的一种类型，如果矩阵的Drazin逆存在，则Drazin逆必唯一。

若存在正整数s， 使得As=0成立，则称矩阵A是s-幂零的，满足条件的最小正整数s称为矩阵A的指数。

分块矩阵的Drazin逆表示目前已有大量成果涌现[1-12]，但没有条件限制的Drazin逆表示现在仍然是一个开放性问题，本文直接从分块矩阵着手，通过把分块矩阵逐个拆分，然后结合Drazin逆的性质和利用已有引理，给出分块矩阵分别在简单条件AB=0，CB=0和AADC=0，AADD=0，AB=0，CB=0下Drazin逆的新表示。

为便于给出分块矩阵Drazin逆的表示，下面首先给出几个重要的引理。

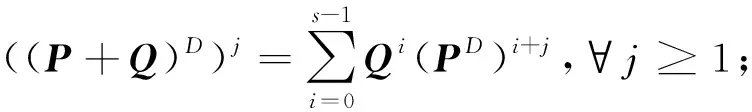
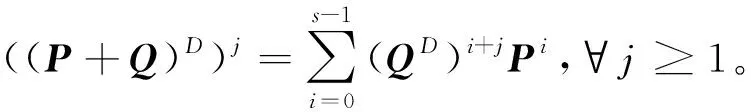
其中，t=max{ind(P),ind(Q)}。

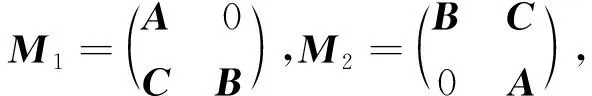
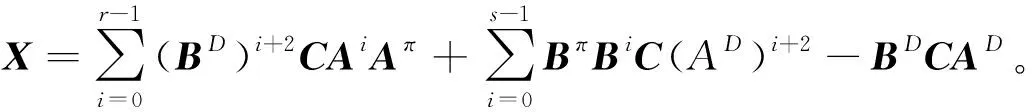
1 主要结果

下面应用引理1—3给出在AB=0，CB=0条件下分块矩阵Driazin逆的表示，以及在AADC=0，AADD=0，AB=0,CB=0条件下分块矩阵的Brazin逆表示的结果。

首先，给出分块矩阵在AB=0，CB=0条件下Drazin逆的表示。

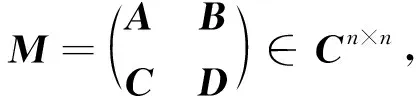
(1)

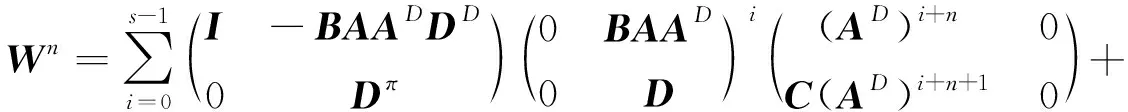
MD=ND+L(ND)2。

(2)

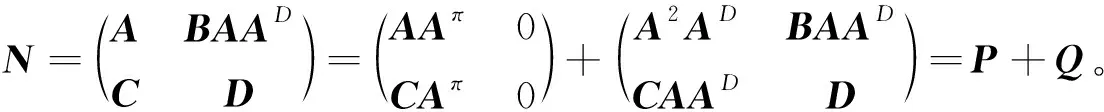
(3)

再拆分Q：

由条件AB=0，可得UV=0，由引理2，

(4)

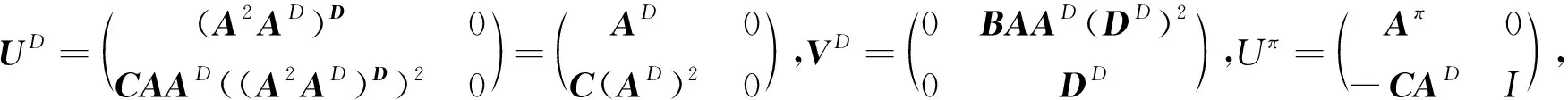
接下来给出在AADC=0，AADD=0，AB=0，CB=0条件下分块矩阵Drazin逆的表示，这个定理实则为定理1的特例。

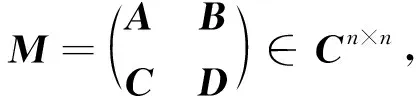
(5)

(6)

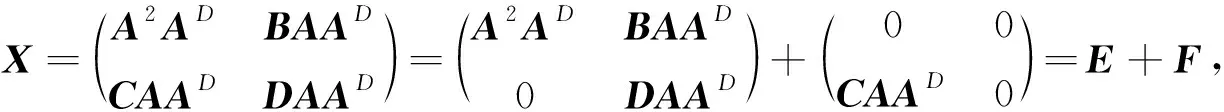
XD=ED+F(ED)2,

(7)

显然，(A2AD)2=AD，由AADD=0，得(DAAD)D=0，再由AB=0，ADB=0，再结合引理3，可得

(8)

将(8)式代入(7)式，可得

(9)

进而，

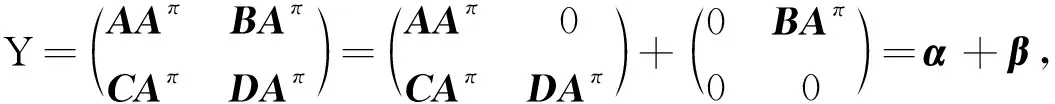
YD=αD+β(αD)2=0。

(10)

接下来把α分成

由ind(A)=l，通过计算α1l+1=0，可得：α1为l+1阶幂零矩阵，显然α1α2=0。

由引理1，可得

(11)

将(11)代入(10)，可得

(12)

将(9)式与(12)式代入(6)式，得(5)式成立。

2 数值算例

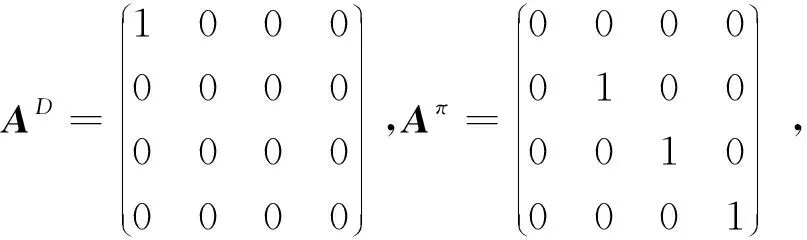
下面给出一个数值例子来验证定理2的正确性。

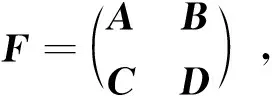
3 结 论

本文直接借助分块矩阵其中一个块的Drazin逆，利用已有的2个矩阵之和Drazin逆的表示，进而给出在简单的条件下分块矩阵Drazin 逆的新表达式，结果更具有一般性。