基于前景理论的高速铁路客流分配方法研究

唐琼华，丁 奇，佟 璐

（北京交通大学 交通运输学院，北京 100044)

0 引言

截至2021年12月31日，我国高速铁路运营里程已突破4万km。2021年全国铁路动车组旅客发送19.2亿人，同比增长23.1%。客流分配是在给定的预测客运需求的前提下，通过刻画旅客的出行行为，研究需求在服务网络上的选择分布问题。该问题的解决对于改善运输资源使用效率、提高旅客运输服务品质、提升高速铁路运输系统经济效益具有重大意义。

高速铁路客流分配的研究主要包括旅客出行行为、路径求解算法和客流分配模型及算法。Fishburn[1]提出旅客出行效用大多考虑安全性、快捷性、经济性、舒适度、方便性5大服务特征因素。1979年，Kahneman和Tversky对Simon的有限理性进行了改进，结合经济学和心理学理论建立了前景理论。吴磊等[2]通过仿真实验对比，得出基于前景理论的路径选择模型更符合实际。Manley等[3]认为路径选择是复杂的有限理性认知过程，考虑人的认知、记忆力、偏好等不确定因素。吴鹏等[4]以Dijkstra算法为研究基础，通过综合深度优先进行算法的改进，提高搜索效率。史峰等[5]利用时空网络无圈特性，基于时刻表完成对大规模网络下高速铁路客流分配模型的求解。李文卿等[6]提出了一种无需遍历图而仅搜索开行方案的两阶段K短路算法。

前景理论认为，人类由于受自身局限性的影响，在不确定条件下进行的选择决策是有限理性的。现阶段对基于前景理论下高速铁路客流分配的研究较少，而当列车开行方案、旅客出行费用等条件发生变化后，前景理论中的有限理性特征对旅客的路径选择行为存在不容忽视的影响。因此，运用前景理论完善客流分配方法对进一步匹配高速铁路运输能力与客流需求有重要实际意义。

1 模型构建

1.1 阻抗函数

旅客在选择高速铁路出行时，由于个体出行需求与列车服务水平存在差异，故对不同列车表现出不同的选择行为，选择路径为旅客确定起讫点OD后选择的乘车方案。经综合考虑后，将影响选择行为的主要因素归结为出行时间、舒适度、票价和便利性，得到旅客出行阻抗函数表达式为

式中：Ca为路径a的阻抗值；Ta，Sa，Pa，Ka分别为路径a的出行时间阻抗以及舒适度、票价和便利性的时间阻抗换算值，min；θ，∂，ω，l为对应因素的权重，且θ+∂+ω+l= 1。

出行时间阻抗为列车运行时间、停站时间、旅客换乘时间之和，可表示为

式中：tv(1)，tv(2)，tv(3)分别为列车运行时间、停站时间、旅客换乘时间，min。

舒适度的时间阻抗换算值与列车运行时间和停站次数有关，采用对数函数表示为

式中：u为列车停站次数，个。

票价与列车运行距离和单位距离基础票价成正比，可通过旅客时间价值转换为票价时间阻抗换算值，故票价时间阻抗换算值表示为

式中：μ为高速铁路旅客时间价值，元/min；Lv为列车运行距离，km；pv为单位距离基础票价，元/km。

便利性的时间阻抗换算值与换乘次数有关，旅客的换乘心理感知随换乘次数呈指数增加，故便利性时间阻抗换算值表示为

式中：α为高速铁路旅客感知旅途平均速度，km/min；m为换乘次数，个；δ为换乘影响因子，为平滑Lvm的影响，待标定。

1.2 基于前景理论的旅客抢票时序调整

对旅客抢票行为机理的深入研究，能够进一步匹配高速铁路运输能力与客流需求。旅客在选择出行路径时，不仅考虑时间、费用、便利、舒适等可获得信息的阻抗，通常还会结合历史出行经验调整抢票时间，衡量心理期望路径与可供选择路径的满意程度，得出实际出行路径。将旅客出行计划生成至出行当日的时间段划分为Z个阶段，当旅客形成出行期望后，对第n+ 1次抢票时序的调整规则表示为

式中：zn为旅客第n次出行的抢票阶段；Cn为旅客第n次选择路径的阻抗值；为旅客第n次出行OD对应最优出行路径的阻抗值；λ为旅客调整抢票时序的评判指标，可分析调查得到的统计数据确定。

1.3 基于前景理论的阻抗值修正

根据前景理论，旅客在多次出行时表现出适应性学习行为。即使获得所有可出行路径的阻抗值，若期望阻抗值与当前最优路径的阻抗值偏差在一定范围内时，旅客通常表现出风险偏好，选择历史出行路径 ，否则表现出风险规避，选择当前最优路径。在高速铁路列车不容许超员的限制条件下，旅客受到历史出行经历的影响区别于道路、普速铁路以及城市轨道交通。旅客期望阻抗值的更新标准和出行路径的选择条件可表示为

若当前最优出行路径为a，则旅客第 次出行的期望阻抗值为第n- 1次出行后对该OD的期望阻抗的更新值，可表示为

若当前最优出行路径不为a，则若第n- 1次出行后旅客对该OD的期望阻抗的更新值与当前最优路径的阻抗值偏差在设定范围内时，旅客第n次出行的期望阻抗值不再进行更新。若偏差超出设定范围，则再次进行更新，可表示为

若h(n)= 1，则说明偏差超出设定范围，旅客第n次出行的期望阻抗再次进行更新，可表示为

式中：C(n,i)，C(n,I)分别为旅客第n次出行对路径a和所有可出行路径的期望阻抗值；φ1，φ2为旅客对历史出行路径的2种依赖程度，与旅客自身属性有关，值越大，依赖程度越高；∫为旅客改变路径的评判指标；h(n)为0-1变量，若为1，旅客选择当前最优出行路径；若为0，则旅客选择历史出行路径a。

1.4 动态客流分配模型

基于阻抗函数的修正完善，可构建遍历高速铁路列车开行方案的动态客流分配模型。模型以区间平均席位能力利用率最大为目标函数，可表示为

模型的约束条件具体如下。

（1）换乘次数不超过自定义的最多换乘次数，可表示为

式中：m为换乘次数；mx为自定义的最多换乘次数。

（2）流量守恒约束，即节点流入客流量与节点自生客流量之和为节点流出客流量，可表示为

式中：Bq0为从站点q出行的客流量，人；分别为站点q两侧与其相连的所有服务路网弧段上的客流量，人；G1，G2分别为两侧服务路网弧段个数。

（3）通过该弧段的所有OD出行路径分配客流量总和为服务路网弧段客流总量，可表示为

式中：Bq1,q2为站点q1和站点q2之间弧段上的客流总量，人，且q1与q2在服务路网中相邻；为列车r开行方案构成的各个弧段的客流量，人；Gr为列车r弧段总数，个；为0-1变量；为列车总数，列。

证明 只需证明算子F的两个分量F1和F2连续即可。首先证明F2的连续性。任取Φi=(Si,IiΓ, i=1,2,则

（4）能力约束，即列车各运行弧段中的最大客流量不得超过列车定员，可表示为

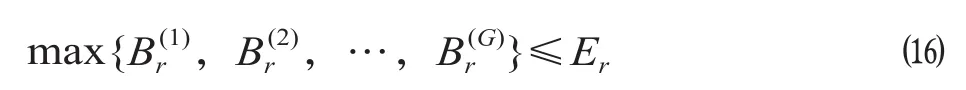
式中：Er为列车r的定员，人。

2 算法设计

对任意起讫点OD，根据4种列车停站序列子集可以确定 取其范围内任意值的备选出行路径，子集的生成规则参考李文卿等[6]既有研究。基于列车开行方案采用容量限制-增量分配法进行客流分配。

出行路径集合搜索完毕后，计算遍历所有路径阻抗可快速搜索出最短路，然后在满足列车容纳量约束的条件下将客流分配至旅客认为最优的出行路径中。分配规则可表示为

式中：Er(g)为弧段g的席位剩余供给客流量，人；B0为预分配客流量，人；BO,D为OD剩余出行客流量，人；B0'为最终分配客流量，人。

每进行一个OD对的客流分配后，更新剩余出行席位供给客流量，若出现服务路网弧段g满足= 0，在g处设置搜索阻碍，算法再次遍历时可自动识别，筛选后生成新的子集。

以此类推，在进行多次迭代后，若对于所有起讫点，都出现公式 ⒅ 至公式 ⒇ 其中一种情况，则代表客流分配完毕。

算法流程如图1所示，其中图1左侧是以动态客流分配模型为主体，图1右侧是基于前景理论的旅客抢票时序调整和阻抗值修正模型实际应用的算法运行流程。

图1 算法流程Fig.1 Algorithm flow

3 案例分析

3.1 旅客自适应学习行为下的客流分配

选取深武高速铁路(深圳北—武汉)为研究对象，对2015年日均客流需求进行分配。旅客在首次购票出行时并未意识到购票时序对购票结果的影响，没有明显的购票时序规律，故在执行算法时，随机赋予第一次出行的每支OD各个阶段抢票人数，抢票人数为在各个阶段表现出准备购票行为的人数之和，即为日均客流需求。同时假设多次出行的需求及供给均不发生变化，旅客在首次出行后形成出行期望，出行期望取旅客出行OD对应最优路径的阻抗值。

令Z取10，所有OD均完成10个阶段的旅客分配表示完成1次出行分配。在分配过程中，考虑到深武高速铁路线路客流的特点，令mx取1，且θ，∂，ω，ℓ按高、中、低月收入3类旅客取值[7-8]，根据长沙、广州、武汉、深圳4市统计局发布的GDP以及人口数据，采用生产法估算得到深武高速铁路2017—2021年间旅客时间价值为72.12元/h。由于研究对象为高速铁路旅客，故根据旅客构成[9-10]时间价值乘系数1.192 7，得到深武高速铁路旅客时间价值为86.20元/h，最终得到μ取值1.43元/min。根据国外的研究，旅客对等待时间的感知是其他时间的3.41倍[11]，高速铁路旅客的平均换乘时间为30 min[12]，平均候车时间取60 min，结合案例深武高速铁路开行方案，最终得到α取值1.82 km/min。暂定δ取0.47。通过初步计算，故分别对评判指标λ取值0.1，0.3，0.5，0.7进行15次出行分配，将取值对应的旅客类型划分为高度敏感型、次高度敏感型、中度敏感型和低度敏感型4类，得到多次出行不同类型旅客同阶段抢票人数变化占比图如图2所示，多次出行不同阶段不同类型旅客抢票人数占比对比图如图3所示。其中出行次数用n表示，人数变化百分比为第n次出行z阶段抢票人数与第n- 1次出行z阶段抢票人数之差除以客流需求；为了更好体现出人数变化的趋势，从第4次出行开始绘制。

图2 多次出行不同类型旅客同阶段抢票人数变化占比图Fig.2 Proportion change in the number of ticket grabbers among different types of passengers in the same stage of multiple trips

图3 多次出行不同阶段不同类型旅客抢票人数占比对比图Fig.3 Proportion comparison of ticket grabbers among different types of passengers in different stages of multiple trips

当实际出行体验与期望存在较大落差时，旅客产生竞争意识，为了获得期望出行路径，抢票积极性不断增强，在图中表现为随着出行次数的增加，在计划生成初期抢票人数变化百分比普遍高于0，且保持动态变化。综合15次出行，高度敏感型旅客的抢票时序调整行为最为显著，稳定趋势较弱。

高度敏感型旅客在计划生成初期抢票的人数普遍高于其他3类，由于列车供给能力有限且远小于需求，故在各个阶段的抢票情况最为激烈。案例将同种类型旅客普遍生成出行计划的时间作为第一阶段来进行研究。以此为基础，能够分析客票预售期内，受到出行目的、出行时间、旅客属性等因素影响下的旅客抢票时序，从而获得需求强度随时间的变化关系，如张宇等[13]所总结归纳的旅客出行需求曲线。

3.2 供给改变条件下的客流分配

基于前景理论，研究当供给条件发生变化后旅客的应对机理，能够得到更为准确的分配结果。选取深武高速铁路为研究对象，基于2015年2月10日的列车开行方案和预测的次年日均客流需求进行客流分配。案例共有上行本线列车17列，车站按顺序编号为1 ～ 18，各列车定员按运行图中列车的实际定员取值，mx，μ，α，δ取值同上。以提高各列车各区间席位利用率为调整方向，对4趟列车的停站进行调整，得到调整后的列车开行方案如图4所示。其中大站表示特等或一等站，小站表示二等或更低等级的高速铁路车站。

图4 调整后的列车开行方案Fig.4 Adjusted train operation plan

令μ1取0.4，μ2取0.3，分别对评判指标∫取值0.1 ～ 0.9进行客流分配，统计区间席位能力利用率和列车载客人数，得到评价指标∫不同取值各区间平均席位能力利用率如图5所示，基于完全理性和有限理性的各区间席位能力利用率如图6所示。由于受到C，φ，∫等多方面因素的影响，当∫取值0.7，0.8和0.9时，多次出行的各区间席位能力利用情况完全相同，故图5、图6不再绘制∫取值0.8和0.9的折线。

图5 评价指标∫不同取值各区间平均席位能力利用率Fig.5 Average seat capacity utilization rate of each interval with different values of evaluation index ∫

图6 基于完全理性和有限理性的各区间席位能力利用率Fig.6 Capacity utilization rate of seats in each interval based on complete rationality and bounded rationality

当∫取9个不同值时，各区间平均席位能力利用在50次分配前均达到了稳定状态，且取值越大，利用率在完成越少出行次数分配后达到稳定值的可能性越大，原因为：当调整列车开行方案后，旅客表现出风险规避和风险偏好2种行为，随着出行次数增加，旅客的理解阻抗值不断更新，最终会固定于某一条或多条出行路径。理性程度越低的旅客群体，改变出行路径的人数比例越低，列车席位利用变化幅度越小，故取值不同不会影响调整列车开行方案后旅客出行分布趋向于动态的稳定状态，同时各区间平均席位能力利用的动态变化反映了旅客的自适应过程，先变化后稳定的现象证明了基于前景理论客流分配的合理性和必要性。

基于完全理性和有限理性的载客人数统计对比图如图7所示。由图6、图7可知，方案调整后前12个区间基于完全理性的列车席位利用率普遍高于有限理性，基于有限理性的总载客人数均高于完全理性，原因为：考虑前景理论后，当某一OD旅客的最优出行路径不同于前一次，且未超出评判指标时，旅客表现出风险规避，不更换出行路径，该资源则被其他OD旅客优先占用。相较于完全理性，在基于有限理性的客流分配中更多短途客流占用了列车席位资源，不仅导致增加的短途客流人数多于减少的长途客流人数，总载客人数增加，而且导致区间席位能力利用率普遍低于完全理性。

图7 基于完全理性和有限理性的载客人数统计对比图Fig.7 Statistical comparison of the number of passengers based on complete rationality and bounded rationality

4 结束语

将前景理论运用于高速铁路客流分配，可一定程度克服阻抗函数中旅客完全理性等与实际决策过程不完全一致的问题，将旅客的出行选择行为拓展至过去、现在及未来的多时空维度进行研究，能够更加动态地刻画旅客心理，提高客流分配结果的精度，验证列车开行方案的调整是否达到优化目标。研究成果对高速铁路的规划、设计与运营具有参考价值，同时也为浮动票价的制定提供了理论依据和思路。由于研究仅选取一条高速铁路线路为对象，存在一定的局限性，因此下一步将围绕前景理论在多条高速铁路线路客流分配中的应用展开研究。