89 GHz多入射角亮温差反演海冰密集度的可行性分析

吴若男，刘浩，吴季

1.中国科学院微波遥感技术重点实验室,中国科学院国家空间科学中心,北京 100190;

2.中国科学院大学,北京 100049

1 引 言

近年来北极海冰面积和厚度均在发生深刻变化（Comiso，2012）。近几年来，尽管海冰几乎只存在于两极地区，它却能在很大程度上影响到全球的生态系统（Cheung 等，2018）。尤其是北极海冰的急剧减少已严重影响到全球生态系统和极地生态系统（Budikova，2009；Stroeve 等，2012），并且已经成为全球变暖的关键例证。北极海冰的减少将会通过大量的反馈机制与气候系统产生相互作用，对北极区域和全球气候产生显著影响，反之亦然（Holland 和Bitz，2003；Vihma，2014；田立军等，2021）。由于海冰是气候的重要组成部分，对海冰的形成、演化和衰减的观测对于理解和预测气候变化是至关重要的，对于研究全球热量平衡也有重要的意义（Holland 和Bitz，2003；Cohen 等，2014）；另外，研究海冰的变化趋势，不仅可以描绘海冰与海水的边界，对于人类开发北极航线，也有重要的实际应用价值（Thomas 和Dieckmann，2010）。其中海冰密集度SIC （Sea Ice Concentration）是研究北极海冰的一个重要参量，定义为给定海洋位置上的海冰面积占总面积的比例，通常用于确定其他重要的气候变量，如冰的范围和冰的体积（Ulaby 等，1986）。因此通过星载探测器观测北洋海冰密集度的分布状况，可为北极海冰的研究提供可靠的基础数据和科学依据（黄季夏等，2020）。

目前，全球海冰产品最主流的数据来源是被动无源微波传感器，其利用开放水域和海冰之间的微波发射率差异使得两种表面类型得以区分。

1972 年安装在美国国家海洋及大气管理局的NOAA 的卫星Nimbus−5 上的电子扫面微波辐射计ESMR （Electrically Scanning Microwave Radiometer）提供最先的海冰遥感图像（Parkinson 等，1987）；1978 年，美国国家航空航天局NASA 的多通道微波扫描辐射计SMMR （Scanning Multichannel Microwave Radiometer）增加了多个频率通道的探测，提供了更为详细和可靠的海冰数据；后来随着传感器的更新，陆续获得了特种微波成像仪SSM/I（Special Sensor Microwave Imager）系列的观测资料，获取多频段以及双极化的亮温数据，利用海冰发射率在不同频段及不同极化下的不同特征来进行SIC的反演（Cavalieri 等，1984；Comiso，1986 和1995），但这些仪器的一个限制是数据的空间分辨率过低。2002 年，安装在Aqua 卫星高级微波扫描辐射计AMSR−E（Advanced Microwave Scanning Radiometer for Earth Observing System），主要基于主频率89 GHz亮温数据反演海冰密集度，利用低频数据为辅进行大气影响修正（Spreen 等，2008），与SSM/I 相比，AMSR−E 的主要优点是利用高频段数据可以实现高空间分辨率，但是其主波段89 GHz 通道的一个缺点是水汽、云液水和降水对亮度温度的显著影响。2012 年5 月，JAXA GCOM−W1 卫 星 上 搭 载 的AMSR−2 传 感 器 替 代AMSR−E 可以提供新的高分辨率数据（赵杰臣等，2017）。中国的FY−3及HY−2系列卫星上均搭载有类似体制的圆锥扫描多频微波辐射计，其观测数据同样可用于海冰密集度反演（张翔等，2012；武胜利和刘健，2018；王晓雨等，2018）。

目前，广泛利用微波遥感数据进行海冰密集度的反演算法主要有3 种：NASA TEAM 算法、Bootstrap算法和ASI （ARTIST Sea Ice algorithm）算法。NASA TEAM算法（Steffen和Schweiger，1991）主要利用SSM/I 的19.4 GHz 的双极化数据（V/H）以及37 GHz 的垂直极化亮温数据；后期改进的NASA−TEAM2 算 法（Markus 和Cavalieri，2000）在NASA−TEAM 算法的前提下，引入85 GHz 的双极化亮温来改善空间分辨率。Bootstrap 算法（Comiso 等，1997）利用海冰发射率随频率的变化以及海冰不同物理特征来计算海冰密集度；但是该算法的不足之处在于对于一年冰和多年冰需要采用不同的频段进行反演。ASI 算法（Svendsen等，1987）利用AMSR−E 和AMSR−2 的89 GHz 亮温数据可以获得目前最高的空间分辨率，并且不需要额外的数据输入；但是在89 GHz 波段下，大气衰减严重会降低海水极化差，使其与海冰的极化差在同一个量级进而在区分海水与海冰时引入误差，并且该算法因为极化差对新冰不敏感导致薄冰区海冰密集度被严重低估（Kaleschke 等，2001），所以该算法额外引入大气滤波器（Weather Filter），利用18.7 GHz和36.5 GHz的梯度率数据做大气影响修正。

综上所述，目前国内外进行海冰探测的微波辐射计多为圆锥扫描方式，双极化（V/H），多频段（6 GHz、19 GHz、37 GHz 和89 GHz），观测入射角通常固定在50°—60°左右。目前的被动微波SIC产品仍存在一些问题：19.4 GHz和37 GHz等波段对海冰密集度的敏感性均高于89 GHz 通道，但分辨率过低，约为12—25 km；89 GHz通道可以实现中空间分辨率6.25 km，但是在大气效应显著的情况下，对海冰密集度的敏感性降低，但对大气状态更加敏感，需要引入大气滤波器进行大气修正。针对上述问题，欧洲提出了哥白尼成像微波辐射计CIMR （Copernicus Imaging Microwave Radiometry）计划并进行预研（Kilic 等，2018），其科学目标主要为高纬度海冰密集度与全球海温测量，目标实现5 km 空间分辨率、5%不确定度的SIC 探测，但是代价是7 m 口径大天线，覆盖L—Ka波段，即频率在4—40 GHz之间。

2009 年发射的欧洲SMOS （Soil Moisture and Ocean Salinity）卫星为海冰观测提供了一种新的技术手段。SMOS 搭载了国际首台星载二维综合孔径辐射计，工作于L波段，其主要科学目标为土壤湿度和海水盐度探测，但在发射在轨之后，由于其低频穿透性及多角度观测的特点，在冰冻圈探测中也获得了重要应用（Kaleschke 等，2010 和2012）。SMOS 独特的二维综合孔径体制可实现对二维视场的瞬时成像，随着卫星平台的运动，地面上的每个像元均可在连续的瞬时二维成像观测中获得多次不同入射角的重复测量，从而获取地面像元的多角度亮温信息（Kaleschke 等，2012）。Mills 和Heygster（2011）利用SMOS 的多角度亮温观测能力提出了一种简单的海冰密集度反演算法，并与AMSR−E 的ASI 算法的反演结果进行了比较，发现在L波段利用多入射角下带来的额外信息可以轻松的辨别海冰与海水。Gabarro 等（2017）利用最大似然估计方法结合SMOS获得的海冰亮温，提出了一种海冰密集度反演算法，并尝试结合极化亮温差与角度亮温差进行SIC反演，发现它们最大限度地扩大了开放水域和海冰之间的差异，SMOS的海冰产品的主要缺陷在于空间分辨率仅有35 km，并且在L波段无法区分一年冰和多年冰，这限制了它的使用。

综合目前现有观测及产品的优缺点，本文提出利用89 GHz 综合孔径辐射计单频多角度观测反演SIC 的设想。多角度观测亮温可通过类似SMOS的二维综合孔径体制实现，毫米波二维综合孔径系统目前在技术上已经较为成熟（Guo 等，2018），其缺点在于所需单元天线数多、复杂度高，工程实现代价大。为简化系统、降低成本，多角度观测亮温同样可以通过一维综合孔径体制配合机械扫描实现。如图1所示，一维综合孔径微波辐射计的扇形波束在顺轨方向可以对目标场景进行多入射角观测，对于同一个像元其入射角通常在−55°—55°范围内变化，在交轨方向进行扫描可实现刈幅覆盖。其潜在优势有：利用89 GHz 波段一维综合孔径辐射计顺轨扫描配合机械扫描可以实现对单个像元点的多入射角观测，充分利用多入射角下的亮温信息可以扩大观测过程中海冰与海水亮温信息的分区，提高SIC 的反演精度，并且实现高空间分辨率。其中的主要问题在于大气路径在89 GHz的波段下对辐射计各通道亮温的影响情况。Schulte等（2020） 在2019 年 初 利 用TEMPEST−D 卫 星（Temporal Experiment for Storms and Tropical Systems Technology）在顺轨方向进行旋转扫描的实验，对卫星地面轨道上的给定的任意大气特征进行数十次独立观测，验证了对同一个像元在不同入射角的观测下亮温可以区分大气状态的实际变化；验证了正演模型的亮温偏差和协方差与入射角之间的依赖关系，并且视角相关偏差大大降低。

图1 一维辐射计顺轨方向多入射角扫描示意图Fig.1 Schematic diagram of multi−incident angle scanning of one−dimensional radiometer along the direction of orbital

本文主要开展利用多角度89 GHz 亮温信息观测北极海冰密集度的可行性研究。首先基于多层海冰辐射传输模型、海水发射传输模型FASTEM−5（FAST Emissivity Model， Verion 5）及大气辐射传输模型MPM （Millimeter−wave Propagation Model）共同构建了星载观测海冰辐射亮温仿真系统，开展了海冰密集度的89 GHz 亮温角度敏感性分析；继而，利用风云三号C 星（FY−3C）搭载的微波湿 度 计MWHS （Microwave Humidity Sounder） 的89 GHz 通道实测亮温数据对仿真结果进行了对比分析及验证；最后，推导建立了基于89 GHz 角度亮温差的SIC 反演算法，结合ECMWF （European Center for Mediumrange Weather Forecasts）的SIC 产品及亮温仿真系统完成了初步反演验证。

2 微波辐射传输模型

海冰和大气辐射传输模型是海冰密集度测量的基础，描述了测量亮温TB（Brightness Temperature）与反演参数之间的关系；同时可以帮助理解在使用星载辐射计进行SIC反演时，盐度、厚度等参量和SIC之间的联系（Ulaby 等，1986）。

由于卫星接收到的辐射一般都包含大气和地表两方面的贡献，因此需要地表辐射模型来反演地表和大气参数。被动辐射计对海冰的天线观测亮温的表达式如式（1）、（2）所示：

式中，TBU为大气上行亮温，TBD为大气下行亮温，宇宙背景对整体亮度温度的贡献被设定为2.7 K，τ为大气的透射率，R为菲涅尔反射系数，TBiceH为海冰的水平（H）极化亮温，TBiceV海冰的垂直（V）极化亮温，TBH为天线观测的H 极化亮温，TBV为天线观测的V极化亮温。

虽然目前已发展成熟的大气、海洋和部分陆地的物理微波模型且覆盖了大范围的微波频率和极化，但这些模型通常不适用于冰雪覆盖的极地地区。目前计算微波海冰发射率模型一共有3 种：经验模型、半经验模型（Tonboe 等，2016）和复杂物理模型。本文利用复杂物理模型计算海冰的发射率。

2.1 数据

本文使用的数据包括FY−3C MWHS 的L1 级亮温数据，ECMWF再分析数据。

FY−3C MWHS 的L1 级亮温数据来源于中国卫星气象中心网站（http：//www.nsmc.org.cn［2020−04−13］）。FY−3C 卫星搭载的微波湿度计MWHS，其频段范围为89—183 GHz，通道数为15，扫描范围为±53.5°，地面分辨率（He 和Chen，2019）为15 km。本文选择MWHS 的第一通道89 GHz 波段下的V 极化亮温数据进行模型的结果验证，时间为2015年1月16日。

ECMWF 利用其预测模型和再分析数据同化系统存档的观测数据，创建描述大气、地表和海洋近期的全球数据集。ERA5 再分析数据由ECMWF再分析数据（https：//www.ecmwf.int/［2020−04−13］）提供，其大气廓线温度、湿度以及云量廓线从地面1000 hPa到高空1 hPa分为37层，选择空间分辨率为0.25°×0.25°。本文选择ERA5地表数据的海冰温度作为海冰模型的输入，选择海水表面温度和10 m 风速作为海水模型的输入参数，选择大气廓线数据作为大气模型仿真的输入，选择云量廓线进行MWHS 观测区域上空的晴空匹配，选择SIC产品数据进行一年冰区域与多年冰区域的筛选，且在后续算法研究中作为量化不确定性的标定。

2.2 多层海冰辐射传输模型

海冰是由海水冰冻而成，其成分主要包括纯冰、液态盐水和空气。由于盐水的相对介电常数较海冰大很多，且随着盐水的不断排出会在海冰内形成空气泡，因此海冰的介电常数在很大程度上取决于盐水和空气的体积（Shokr，1998）。造成海冰散射的重要因素是盐水、气泡的大小和数量及密度（Winebrenner 等，1992），因此不同类型海冰的特性与纯冰之间存在巨大差异。

为计算海冰的复介电常数，首先需要计算盐水的复介电常数、及盐水的体积占比（Ulaby 等，1986）和空气泡的体积占比（Cox和Weeks，1983）。张翔（2012）利用随机介质的强起伏理论计算出海冰的复介电常数，证明它的影响因素主要有杂质的形状和方向、空气泡体积和盐水的介电常数及其体积。

海冰是一种分层介质，简单的模型由于没有考虑层间的重要反射而无法准确模拟观测结果。在此，本文采用多层海冰辐射传输模型（Mätzler，2006），来简短的概述不同的物理参数在多入射角下对海冰的定量影响，其中包括多层介质、表面及层间体散射、层间多次反射等。冰的形成环境、冰的分布、雪的覆盖、冰的表面粗糙度、冰的密度、冰的盐度和冰内杂质的含量等是海冰微波发射率的重要特性（Mätzler，2006）。发射模型描述了这些物理特性和微波测量亮温之间的联系，其中，海冰的散射和介电特性假设在同一层中各向同性。海冰散射系数利用改进的玻恩近似（Mätzler，1998）计算，散射体主要是多年冰中的气泡和空洞，以及第一年冰中的盐水。散射系数是主要由纯冰的介电常数、盐水或空气的介电常数、海冰混合物的介电常数、盐水或空气的体积、微波频率和散射体的相关长度共同决定，其中相关长度（pec）与散射体大小和分布相关（Mätzler，2002）。

在多层海冰辐射传输模型（Wiesmann 和Mätzler，1999）中，海冰被假设成n层（j=1，2，…，n），包含空气—冰、冰—冰之间的层分界（给定频率f、极化p和入射角θ=θn），如图2 所示。在图2 中，冰的亮温为Tice，最底层的反射率假设为s0，最底层亮温假设为T0，层间的反射率为sj，层内的反射率假设为rj，层内亮温Tj，发射率ej，传导率tj，由能量守恒可知rj+ej+tj=1，下行大气辐射亮温为Tsky，层厚为dj，层数为n。

图2 多层海冰辐射传输模型示意图Fig.2 Schematic diagram of multi−layer sea ice radiation transmission model

多层海冰辐射传输模型属于复杂物理模型，完全基于物理关系建立，其优点是可以在不进行大量北极海冰实地观测工作的情况下建立海冰发射率模型，为SIC反演提供依据。且多层海冰辐射传输模型适用频率范围1—100 GHz，模型结果计算准确。因此，本文利用多层海冰辐射传输模型对北极海冰的前向仿真亮温进行建模，作为后续研究SIC反演算法的基础。

2.3 海水及大气辐射传输模型

本文选择FASTEM−5 海水发射传输模型。该模型的早期版本计算介电常数使用双Debye 模型，缺点是没有包含对海水盐度的敏感性（Ellison 等，2003）。在后续的FASTEM−4 和FASTEM−5 版本中，利用测量数据开发了新的复介电常数模型（Liu 等，2011），其适用频率为1.4—200 GHz，海水物理温度为−2—30 ℃，盐度范围为0—40 psu。

本文采用微波大气辐射传输模型MPM。MPM模型（Liebe，1989）将复杂的大气物理变化利用微波理论进行描述，为仿真大气系统提供了一种简单有效的方法；MPM 模型内部具有多套程序，每个程序都提供了针对特定传播障碍的最实用的仿真方法，并通过理论和准确的测量进行了校正及验证。为简化模型复杂度，通常会假设大气是水平均匀的；其中，在89 GHz 频段，对于无降雨的情况，大气对亮温的影响主要表现为氧气、水汽和云液水的贡献。

3 模型结果及验证

3.1 模型输入数据

仿真模型首先利用ECMWF 再分析数据ERA5为海水建模提供海面温度（K）、风速（m/s）等，为大气建模提供大气廓线及地表输入数据，包括时间（十进制）、大气压强（hPa）、大气温度（K）、水汽密度与液态水密度（g/m3）；其次，从获取的地表表面数据对海冰每一层有如下预测参数：海冰温度、密度、厚度、冰的盐度和冰内液态水含量。

表1所示的海冰剖面是按从下到上的顺序排列的，每一层的参数如下：层数（j），厚度（d），密度（ρ），相关长度（pec），盐度（S），物理温度（T），液水含量（W），海冰介电常数（ε）。其中，海冰层温数据选自EC 地表数据，其余参数参考文献（Mätzler，2006；Ulaby 等，1986）。对于海冰来说，一年冰及新冰盐度通常在5—10 psu，而多年冰的盐度由于盐水不断的在夏季析出通常为0—1 psu；海水盐度假设为35 psu。夏季的融化过程是复杂的，该模型对其描述不够充分。因此，本研究不包括夏季融雪。

表1 多年冰和一年冰剖面的模型输入参数Table 1 Model input parameters of multi-year and first-year ice profiles

3.2 模型仿真结果

图3（a）和3（b）分别显示了仿真的表面亮温及天线观测亮温下海水、一年冰与多年冰分别在水平极化和垂直极化下亮度温度与频率的关系，其中入射角假设为55°。不难看出，随着频率的升高，海水的亮温不断升高，但是海冰的亮温不断下降。因为在89 GHz，穿透深度很浅，因此只有海冰表面亮温贡献（Ulaby 等，1986）。而多年冰明显比一年冰下降的更快，因为多年冰表面凹凸不平，且内部空气泡的增多导致散射在高频时更明显。

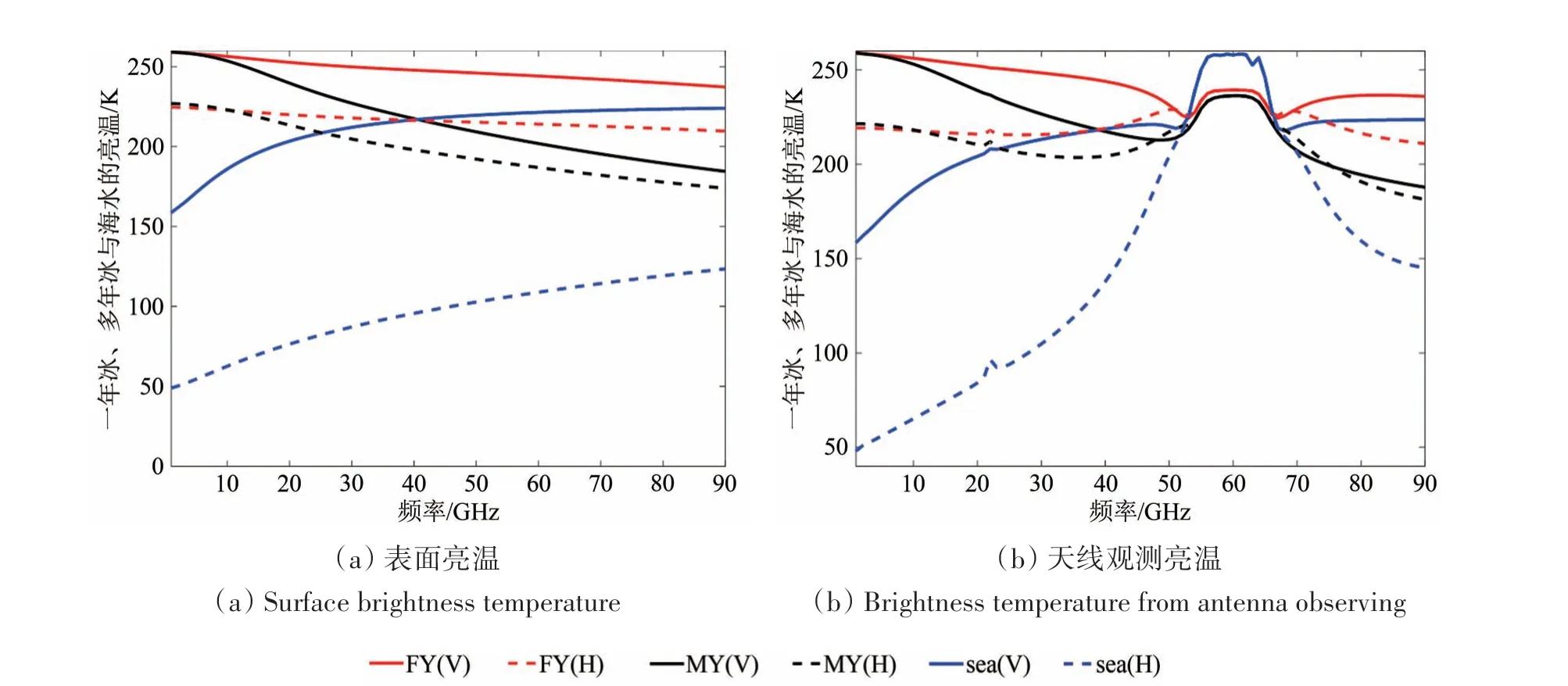
图3 一年冰（红）、多年冰（黑）与海水（蓝）亮温在频率0—90 GHz的变化，入射角为55°Fig.3 Brightness temperature of first−year ice（red），multi−year ice（black）and seawater（blue）vary in the frequency range of 0—90 GHz respectively，with an incidence angle of 55°

3 种表面类型的89 GHz 亮温变化随入射角的关系，如图4（a）所示，结果显示，海水的极化亮温随入射角的增加变化更加明显，而海冰的极化亮温对入射角并不敏感，并且3 种表面类型的H极化亮温变化均大于V 极化亮温变化；其中需要注意的是，北极海冰在全年非表面融化状态下，均通常伴有一定的积雪，深度通常在几厘米至几十厘米间，并与冰类型有关。对于89 GHz 的微波浅层穿透（深度约为积雪的上方几厘米），积雪对表面探测亮温会产生非常重要的影响，即89 GHz的发射率对具有一定深度积雪覆盖的海冰的类型基本上是不敏感的，意味着不同类型的海冰与积雪有相似的辐射特征。积雪覆盖下的海冰亮温变化如图4（b）所示，其中积雪的输入参数及仿真方法参考文献（Mätzler，2006）。图4（b）结果显示，对于积雪覆盖的海冰，积雪的存在会增加海冰表面亮温，降低对于海冰类型的分辨；但是，冰雪表面的垂直极化亮温随着入射角的增加，增长趋势更为缓慢，增大了海冰与海水的角度亮温差异。由于积雪输入参数的可变性较大，会增大模型的不确定性，因此后续研究均选择无积雪的海冰模型。

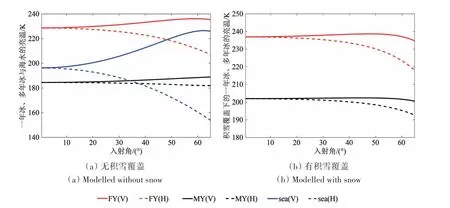
图4 一年冰（红）、多年冰（黑）与海水（蓝）亮温分别在频率为89 GHz时随入射角在0—65°内的变化趋势Fig.4 Variation trend of the brightness temperature for first−year ice（red），multi−year ice（black）and seawater（blue）with the incidence angle within 0—65°when the frequency is 89 GHz，respectively

为研究图4 中海冰与海水亮温对入射角的响应， 本文定义两个指标： 极化亮温差PD（Polarization brightness temperature Difference）定义为参量的垂直极化亮温与水平极化亮温的差值，如式（3）所示；角度亮温差AD （Angle brightness temperature Difference）定义为在V/H 极化下，随Δθ变化的角度亮温差值，如式（4）所示，以V极化为例。

图5 表示当入射角为55°、频率为89 GHz 时，垂直极化与水平极化亮温的差值；图6（a）表示Δθ在0—65°之间变化的亮温TB（Δθ）与θ=0°时的亮温TB（0°）的差值；图6（b）表示当Δθ=30°时，θ在0—35°之间变化时，TB（θ+30°）与TB（θ）之间的亮温差值。从图5 和图6 的结果可以看出，海冰与海水的PD 以及AD 相差很大，因此二者皆可以作为判别海冰与海水的标志。

图5 一年冰、多年冰与海水的极化亮温差（PD）分别在频率为89 GHz时随入射角0—65°内的变化趋势Fig.5 Polarization brightness temperature difference（PD）for first−year ice，multi−year ice and seawater changes with the incidence angle within 0—65°when the frequency is 89 GHz，respectively

图6 一年冰（红）、多年冰（黑）与海水（蓝）分别在频率为89 GHz时的角度亮温差（AD）的变化趋势Fig.6 Variation trend of the angle brightness temperature difference（AD）for first−year ice（red），multi−year ice（black）and sea water（blue）when the frequency is 89 GHz，respectively

上述仿真中，海水为基于ECMWF 再分析个例数据（2015 年1 月6 日），海冰为基于表1 作为亮温模型输入参数的典型结果；实际上，由温度、盐度、风速和厚度等物理参数变化而引起的海水/海冰表面辐射率变化必须予以考虑。表2 参考Gabarro等（2017）列出了根据理论模型利用I指标（I=TB，PD和AD）对冰和海水的地球物理变量进行的敏感性分析。定义敏感系数为∂I/∂P，P代表海冰与海水的物理温度T、盐度S和10 m 风速W。三者的变化范围为：海水物理温度变化区间273—288 K，盐度变化区间30—38 psu，风速变化区间为5—15 m/s；海冰物理温度变化区间250—270 K，海冰盐度变化区间0—14 psu。由于89 GHz 探测频率对海冰厚度和冰上风速并不敏感在此不做考虑。由表2 结果可知，对于海冰而言，AD指标对物理温度、盐度的敏感性显著低于PD和TB指标；对于海水而言，AD对温度与风速的响应较大，但也低于PD。

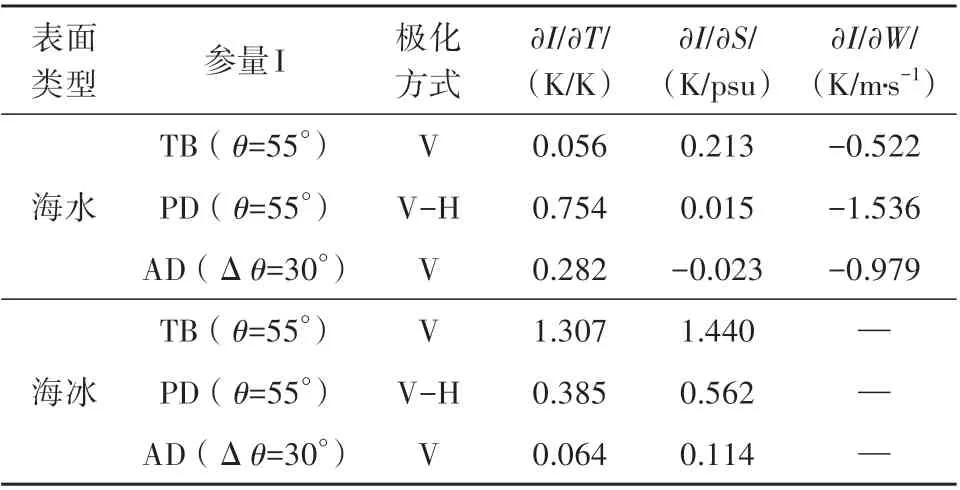
表2 海水和海冰的TB、PD与AD对物理温度（T）、盐度（S）、风速（W）的敏感性分析Table 2 Sensitivity of simulated TB，PD and AD to temperature（T），salinity（S）and windspeed（W）

本文后续均利用垂直极化亮温的角度亮温差进行海水与海冰的区别验证，一是因为图6显示海冰的垂直极化亮温对角度敏感性低于水平极化亮温，可以保证海冰与海水的垂直极化角度亮温差在不同入射角下更有区分度；二是因为后续采用的验证载荷MWHS 的89 GHz 通道只有垂直极化观测亮温，方便进行模型与实测数据的对比。

3.3 MWHS数据验证

MWHS 的扫描角范围为−53.3°—53.5°，以1.1°为间隔共扫描98 个点。按照式（5），可知其地面入射角θEIA的范围为−65°—65°。

式中，θ表示载荷扫描角，h表示载荷与地面的高度，r表示地球半径。

图7 所示为ECMWF 提供的北极海冰密集度日分布，时间为2015 年1 月16 日；其中，对于纯冰区域与纯水区域，本文参考文献（Tonboe，2010）选取固定的区域亮温值，蓝色框内所示区域代表多年冰，纬度取北极81°—85°N，经度为130°—150°W；黑色框内区域代表一年冰及新冰，纬度取北极81°—85°N，经度为140°—160°E；红色框内区域代表海水，北极纬度50°—55°N，经度10°—22°W。

图7 2015年1月16日北极海冰密集度分布Fig.7 Arctic sea ice concentration distribution，the date is January 16，2015

图8 展示了所选一年冰区域与多年冰区域从2012年1月—2016年1月的SIC日数据变化，从图8中可以看出所选区域在夏季时，一年冰区基本融化，而多年冰区只有少部分融化。

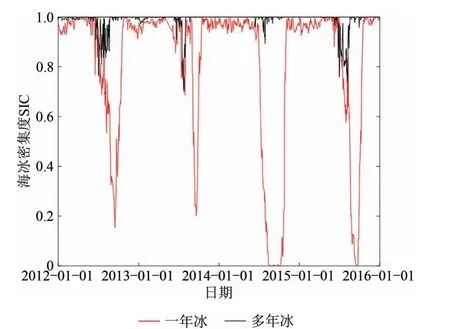
图8 一年冰（黑）区与多年冰（红）区的SIC变化Fig.8 SIC change for first−year ice region（black）and multi−year ice region（red），respectively

分别对多年冰、一年冰及海水3 个区域利用MWHS 的亮温数据研究V 极化亮温与入射角的关系。为避免恶劣大气带来的亮温误差，利用EC 数据进行晴空匹配。其中晴空的判断条件根据EC 的云量廓线，海冰上空云量廓线小于0.1 时判断大气路径为晴空；而海水上空因为含云量多，为避免筛选后数据不足，选择其廓线小于0.2，经纬度匹配范围在0.25°，时间匹配范围在2 h以内。

多年冰、一年冰、海水的亮温随入射角的变化如图9所示。由观测结果可知，多年冰的亮温变化在180—190 K 浮动，而一年冰亮温变化在220—230 K 内浮动，二者的亮温皆随入射角的变化并不明显。海水的亮温变化范围较大，在200—250 K浮动，并且海水的亮温随入射角的增大而增大，在小入射角时，变化并不明显，当入射角越大时，增长速度越快。对MWHS 的亮温数据做晴空筛选后的亮温与入射角的关系并无明显变化。图10 为晴空筛选前后的亮温中值变化，3 种表面类型的亮温中值与入射角的线性关系基本趋于一致。

图9 MWHS的3种类型天线观测亮温在多入射角（0°—65°）下的亮温分布Fig.9 Observed brightness temperature distribution of the three types of MWHS at multiple incident angles（0°—65°）.

图10 MWHS经过晴空校准前（红）与后（黑）的3种类型的天线观测亮温在多入射角（0°—65°）下的亮温中值关系对比Fig.10 Comparison of median distribution of the observed brightness temperature between clear sky（Red）and normal atmospheric（Black）of the three types of MWHS at multiple incident angles（0°—65°）

3.4 MWHS验证结果分析

利用EC 地表及大气廓线数据，与本文建立的辐射传输模型分别对图7中多年冰、一年冰及海水这3个区域的海表类型进行亮温仿真，并与相匹配的MWHS 实测亮温进行统计分析，具体误差结果见表3。

表3 中，参量TB 表示在入射角θ=0°时，多年冰、一年冰与海水的仿真亮温与实测亮温的中值与标准差σ。AD 表示三者角度亮温差的对比，其中选择两组角度差，分别为AD（55°—20°）与AD（35°—0°）。RMSE 表示仿真亮温与实测亮温之间的均方根误差，其中参量TB（θ=（0°—65°））表示入射角为0°—65°时的均方根误差，AD（θ=（0°—30°），Δθ=（0°—30°））表示初始角度θ在0—30°、Δθ=30°内变化的角度亮温差。

从表3中仿真模型与实测结果的展示中均可以看出：海水与海冰的角度亮温差（AD）存在明显区别，因此可以通过统计方式得到区分海水与海冰的边界点，并为利用AD 进行海冰密集度的反演算法研究提供了理论及数据验证；在89 GHz 时一年冰亮温比多年冰高，因此在高频波段，海冰年限与亮温成反比关系成立，后续可以利用在固定入射角下的亮温的大小判断海冰年限。

仿真数据与实测数据存在一定的误差，主要原因如下：

（1）MWHS 实测的海水区域的亮温与仿真亮温相比，亮温量级区间基本相同，但是海水区域的MWHS的AD数据均比仿真的低，主要原因是表3中的MWHS 数据采用图10 的中值数据，而图10 展示海水在35°—45°之间的亮温中值有降低现象。主要原因在于：首先，在大入射角下，水平大气的不均匀性会对亮温有一定的衰减，尤其MWHS的交轨扫描方式导致两个入射角下的大气路径不同且长度相差巨大，也会加重海冰与海水的角度亮温差的区别度降低；其次，海水亮温是由海水温度、风场、大气情况共同决定的。模型输入的海面温度为0点时的物理温度，夜间水温较白天的低会降低海水的发射率。模型输入的风速与风向的时间为固定的2015 年1 月16 号0 点值，但是MWHS 测量值下的风速为实时风速，海上风向与风速变化快，因此模型输入的风向与实时风速相差较大，风速的偏差会对粗糙海面发射率造成影响；同时，海水上空云量较多，水汽和液水等大气效应导致的探测误差相对海冰区域更加严重。因此，MWHS 的海水亮温趋势因为一天内物理参数的不确定性太多，只能初步证明海水的垂直极化亮温与多入射角的关系，不能进一步的利用。

（2）一年冰的数据与仿真相比，对角度的敏感性更地，并且亮温量级低10 K 左右。原因是一年冰区分布更复杂，新冰及薄冰占比大，有些小区域存在较多较小的碎冰块，夏季一年冰区会反复融化又结冰，造成海冰表面物理参数变化区间大，模型无法准确的进行描述。同时也造成在同一角度下，MWHS 对不同像元的观测亮温数据会产生较大跨度。

（3）从MWHS 的3 种表面类型的亮温散点图来看，单入射角下的亮温变化区间大，分布并不均匀，线性度较差，主要原因是MHWS 采用交轨多入射角扫描，在其宽刈幅内并不是对同一个像元而是分别对其98个观测点进行的多入射角观测，上述分析结果受到单次扫描刈幅内地表亮温均匀性的影响，与理论分析存在一定误差。

（4）理论模型具有一定的不确定性，如表2所示。在表3 的区域仿真中，使用ERA5 的表面温度作为辐射传输模型的输入，以及积雪、一年冰与多年冰的输入物理参数（盐度，密度等）在理论范围内均为随机性输入，均会对模型仿真亮温造成系统性偏差。

表3 一年冰、多年冰与海水的仿真与实测的亮温与角度亮温差及二者均方根误差Table 3 Brightness temperature，angle brightness temperature difference and their root-mean-square error between simulated and measured for first-year ice，multi-year ice and seawater

4 海冰密集度的反演算法与验证

4.1 基于多入射角亮温差的海冰密集度反演算法

混合像元的亮度温度，即部分被海冰覆盖的海洋像元可以表示为海冰与海水的亮度温度的线性组合，并以每种表面类型的百分比进行加权组合（Comiso 等，1997）。

式中，TE表示观测点亮温，Tice表示海冰亮温，Twater表示海水亮温，CT是指该像元中冰的比例，即海冰的密集度，当CT=1时表示该像元拥有100%的冰，相反，当CT=0时表示该像元均是海水。

ARTIST 海冰算法（ASI） 最初是为了利用SSM/I传感器的85 GHz通道的高空间分辨率来对边缘海冰的极地大气边界层进行中尺度数值建模而开发的，该算法是利用极化差反演SIC，利用低频数据进行大气误差的校准（Kaleschke 等，2001）。本文将角度亮温差AD取代极化差PD，修改ARTIST算法，验证海冰密集度的反演与角度差之间的依赖关系。

对于89 GHz 频段，天线接收亮温必须包括大气的贡献（Svendsen 等，1987），下行辐射的反射和上行大气辐射的发射和吸收都包括在内，其中观测点表面辐射亮温TE=εTS，由于3 mm 电磁波在海冰中的穿透深度非常小，TS表示平均物理表面温度，对于水平均匀的大气，观测点的亮温如式（7）：

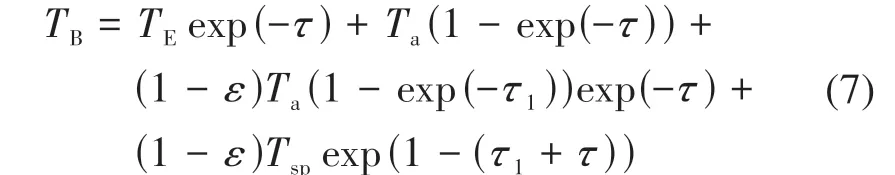
式中，TB表示天线观测亮温，Ta表示大气的有效物理温度（为简单起见，假设高度不变），Tsp表示宇宙背景温度，假设为2.7 K，τ表示上行大气辐射的光学厚度，τ1表示下行大气辐射的光学厚度，在表面接近镜面反射的水平均匀分层大气中；假设τ=τ1=τ0secθ，其中τ0表示垂直入射光学深度，θ表示入射角。

根据Svendsen 等（1983）提出的近似，本文在此假设Ta≈1.11TS，Tsp/TS≈0.01。综上，在入射角分别为θ1和θ2时，则式（7）可以表示为：

根据式（6），不同入射角（θi）下的表面亮温可以表示为：

将式（9）代入式（8），角度亮温差AD 如下所示：

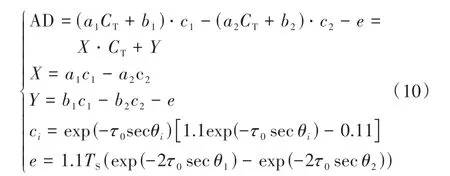
卫星在扫描轨道内的足迹总能测到一些纯冰（CT=1）以及冰边缘的纯水（CT=0），并且二者的大气透射率近似相等。当在开放水域即CT=0 时，角度差AD0如式（11）所示，同理，当CT=1 时即在完全冰覆盖区域AD1如式（12）所示：

式（10）在趋近于CT=0 和CT=1 时如果假设对于完全被冰覆盖或开放水域，大气影响近似相等并且变化很小，海冰的密集度可以表示为

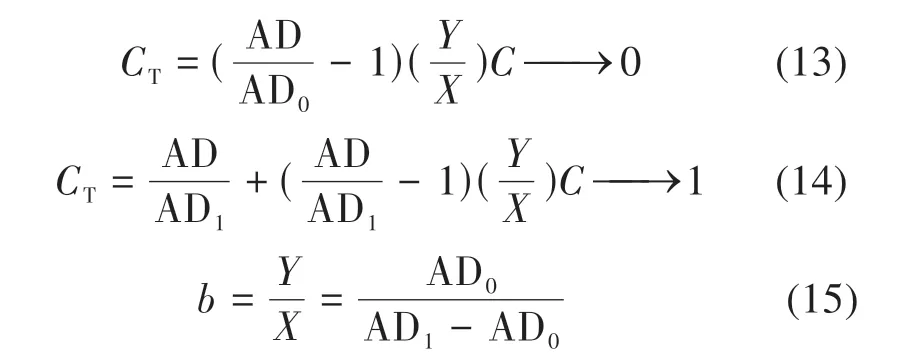
为了能够获取0%到100%之间的所有海冰密集度值，需要在式（13）和（14）的解之间进行插值。选择开放水域和全覆盖冰盖之间的海冰密集度的三阶多项式表示方式：

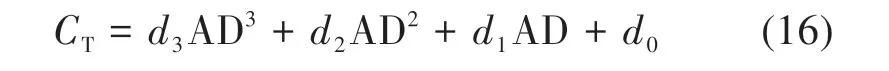
利用式（13）—（16）及其一阶导数，可以通过求解线性方程组来确定式（16）中的未知数di：

根据式（17）可以得到方程组的系数d0—d3的值，利用式（16）来计算海冰密集度，此时需要知道已知开放水域以及100%的海冰覆盖率的AD0和AD1的系点值。利用系点值结合式（16），海冰密集度公式可以表示为：

因为系点值还包括平均大气影响，正确选择系点值对海冰密集度的反演具有重要意义。在原有的利用极化差进行反演的ASI算法中，判断纯冰与纯水可以选择固定系点值或动态系点值，并形成了针对不同大气条件下的自调整过程（Svendsen等，1987；Spreen 等，2008）。

4.2 单入射角反演算法验证结果及分析

为验证海冰密集度与多入射角亮温差之间的关系，本文共选择两个冰水混合区域建立亮温仿真模型，位置如图11 所示，其中，绿色框区域表示区域1，选择75°N—79°N，35°E—45°E；黑色框区域表示区域2，选择75°N—79°N，0°W—10°W。

图11 冰水混合区域海冰密集度分布图Fig.11 Distribution of sea ice concentration in ice−water mixing regions

本文利用式（6）模拟混合区域的亮温分布：第一步，利用第2 节中的海冰、海水与大气模型，仿真−55°—55°入射角下的纯一年冰、纯水区域亮温分布，其中一年冰的物理参数在可选的范围内随机输入来模拟海冰类型不均匀性，海水的物理参数来自ECMWF 再分析数据；第二步利用来自ECMWF 中混合区域内的海冰密集度产品CE，作为式（6）的输入参数，模拟冰水混合区域的天线端亮温TE，三者采用相同大气数据。

在本节的仿真系统中，对区域亮温分别加入高斯白噪声模拟系统灵敏度误差及大气误差。仿真的系点值分别选择第3.2 节仿真的纯海水区域以及一年冰区域，分别利用两个区域内所有像元点的角度亮温差的平均值作为辨别海水与海冰的边界点。

简单的选择3组角度的亮温差对两个冰水混合区域进行海冰密集度反演，分别为：

在仿真系统中分别加入高斯白噪声0—3 K，为简化仿真，加入噪声未考虑综合孔径辐射计灵敏度随视场角的变化。以0.2 K 为步长统计模型输入CE与反演得到的CT之间的均方根误差（RMSE），如图12所示。

图12 3个区域利用单组角度亮温差：A1（黑）、A2（红）、A3（蓝）得到反演SIC与仿真输入SIC在对应输入的高斯白噪声下的均方根误差（RMSE）Fig.12 Root mean square error（RMSE）of SIC on retrieval using A1（black）and A2（red）and A3（blue）respectively，and simulation input SIC in two regions under the Gaussian white noise of corresponding input

从图12 中可以看出，A1的误差明显比A2和A3更大，这是因为在小入射角时海冰与海水的亮温差对比不明显，而在大入射角时，海水的亮温增幅比海冰增长更快，所以利用大入射角，如30°至60°区间内的角度亮温差反演可以得到更准确的结果；A3的反演误差比A2的低，可见，采用角度差区间越大越有利于分辨海冰与海水；同时发现在输入的高斯白噪声为0 K 时，误差约为0.007 左右，这是在各种假设下所具体采用的系点所导致的误差，真实情况的系点确定及相应误差需另行考虑。

实际上，基于图1 中所展示的在轨观测几何，一维系统对于单个观测点可以获得连续的观测角度，比如−55°—55°。利用多组角度差组合（A1，A2，…，Aj，j=1，2，…，N）反演得到的SIC 进行后处理加权平均可进一步降低反演误差。

4.3 连续入射角反演算法验证结果及分析

利用4.2 节的单入射角反演算法，选取连续入射角间隔为N，可以连续反演得到SIC1(θA−θB)，SIC2[(θA−1)−(θB−1)]，…，SICN[(θA−N) −(θB−N)]，因为卫星运行中对单个像元点可以获得正负两组角度，事实上可以获得2N 组角度差。对上述2N组SIC结果根据各自的RMSE进行最小均方根误差加权平均处理，求得最终的SIC。

为验证利用多组角度差进行最小均方根加权平均后处理可以降低反演误差，本文针对4.2 节中的两个区域，分别选取三组连续角度差，如表4所示，通过加权平均方法进行SIC 反演，高斯白噪声区间为0—3 K，统计输入CE与最终反演得到的CT之间的均方根误差，如图13所示。

图13 两个区域利用连续角度差S1（黑）、S2（红）、S3（蓝）得到反演SIC与仿真输入SIC在对应输入的高斯白噪声下的均方根误差（RMSE）Fig.13 Root mean square error（RMSE）of SIC on retrieval using S1（black）and S2（red）and S3（blue）respectively，and simulation input SIC in two regions under the Gaussian white noise of corresponding input

表4 连续入射角组合Table 4 Continuous incidence angle combination

从图12 和图13 的对比中可以看出，二者皆是利用大入射角的亮温差反演效果更好。同时，当误差标准为5%时，利用连续入射角亮温差最高容许的噪声为2 K 以上，而单入射角亮温差对应最高噪声仅为1 K。二者具体反演精度如表5 所示。以区域1为例，分别展示单入射角度A3与连续入射角组合S3在固定噪声下的RMSE。从表5 的对比可以看出：连续入射角组合可以充分利用多入射角亮温信息进一步的降低反演误差，利用RMSE加权平均的方法可以在充分利用小入射角的亮温同时最小程度的降低小入射角带来的反演误差。

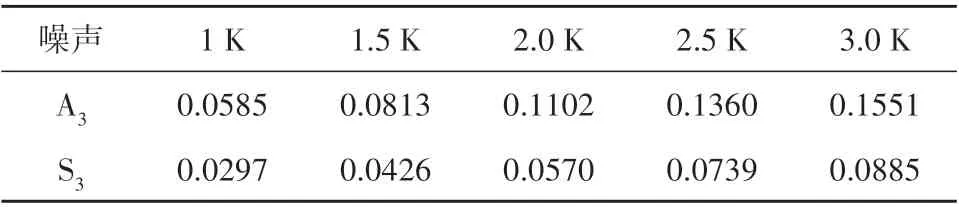
表5 区域1下的单入射角与连续角度组合的RMSETable 5 RMSE for single incident angle and continuous angle combination under region 1

参考CIMR 预研的5%的SIC 误差标准，采用误差较小的连续入射角S3组合，模型输入高斯白噪声系数为2 K，将仿真反演得到的SIC 与仿真模型输入的ECMWF 的SIC 数据进行线性拟合。图14展示两个区域仿真得到的拟合结果。总体来看，反演得到的海冰密集度整体偏低，但是在纯海水区域均会有不同程度的高估。两个区域反演得到的SIC总体偏低，这是因为本次模型选取的新冰区域，处于反复融化又结冰的复杂过程，海冰表面状况复杂，模型对此种类型冰的输入数据无法做到完全正确；与输入SIC 相比，在纯水区域会有虚假浮冰，这是因为加入的噪声会降低海水角度差，使其低于海水系点值，导致在纯水区域反演得到的SIC增大。因此后期利用更多的亮温信息进行低密集度区域的校正尤为重要。

图14 两个区域的仿真输入SIC与反演SIC的线性关系；其中，高斯白噪声为2 K，连续角度差组合选择S3Fig.14 Linear relationship between SIC on retrieval and simulation input SIC in three regions where Gaussian white noise is 2 K and S3 was selected as angle difference

需要注意的是，本文仅是选择MWHS 交轨扫描点，无法获取单个像元的多入射角响应亮温，因此只能借助模型证明海冰与海水的亮温随入射角的变化趋势，以及利用角度亮温差进行SIC反演的可行性分析。利用仿真亮温系统进行反演算法的验证具有一定的局限性：首先，实际过程中，海冰与海水的系点值的选取会影响到SIC的反演精度，本文利用加入噪声后有限仿真亮温下的平均值作为系点值，理想化的建模是会在一定程度上降低真实系点值的误差，因此真实情况下的系点值误差需要后期另行考虑；其次，对于模型而言，冰上的雪层，大气中的水汽、液态水以及海面的物理温度和风场的实时变化均会造成实际探测亮温的波动，会对SIC 的反演带来一定的影响，仿真中并未考虑在内。

本文提出的利用多入射角亮温差进行SIC 反演的方案，对于冰水边缘区以及夏季冰区的SIC 研究还有一些改进与后续工作如下：

（1）本文研究显示，在89 GHz波段下，SIC对单个角度亮温差（AD）的敏感度略低于极化亮温差（PD），并且新冰及一年冰对AD 敏感性略低于多年冰区。因此本文第4节选择冰水边缘区进行反演，发现利用单组角度亮温差对海冰边缘区域、薄冰及新冰区域有些许低估，对于亮温稳定的多年冰区反演效果最精准。但基于本文提出利用多角度加权平均算法可以充分利用不同角度下的亮温信息，显著减少对于边缘区的低估误差，优于利用单组PD 的反演效果。因此对于海冰边缘区，后续可通过优化角度差组合、系点值及算法来进一步扩大多入射角联合反演的优势。

（2）对于冰区而言，亮温在非夏季时间段趋于稳定，在夏季时由于冰雪融化会降低海冰的发射率。但是，如表2 所示，海冰AD 相比于亮温和PD，其对物理参数的变化响应最低。因此夏季时，物理温度升高和盐度的变化虽然会最大程度上影响海冰的亮温量级，但是相对于PD，季节的变化对于AD 的影响最小。因此对于夏季海冰的SIC 反演，使用AD 相对于PD 理论上会降低反演误差。同时，在冬季和夏季分别利用不同的系点值更有助于提升SIC 反演精度。Gabarro 等（2017）利用SMOS 探测数据证明单组角度亮温差相对于PD 对薄冰区及夏季海冰SIC 反演效果更好。因此，利用多组角度亮温差有潜力进一步提升被动微波对SIC的探测能力，改进目前在海冰边缘区、夏季等存在的问题，后期对该理论在海冰边缘区和夏季冰区的探讨还具有很大的发展空间。

5 结 论

本文主要介绍了一种利用89 GHz 角度亮温差进行海冰密集度反演的初步验证。目前国际上针对海冰密集度开发了多种算法，大部分均利用海水与海冰在双极化亮温差上的差异，以及利用多频段亮温信息进行大气校正等。本文提出了利用89 GHz 角度亮温差进行海冰密集度反演的设想。并搭建仿真系统，仿真地表亮温，加入高斯白噪声模拟探测误差，在此基础上，进行多入射角反演算法的验证。

本文研究结果表明：

（1）模型仿真结果显示：随着频率的升高，海水亮温上升，海冰亮温不断下降；随着入射角的增大，海水的垂直极化亮温增长明显，海冰对入射角并不敏感。MWHS 实测数据结果验证模型对入射角的敏感性分析正确，与模型仿真结果趋势一致。

（2）利用连续角度亮温差进行SIC 的反演具有可行性。研究发现：1）利用入射角在0°—35°内亮温差会引进更大的误差。这是因为海水亮温在小入射角内变化不明显，与海冰差异小，导致小入射角内的微小亮温误差均会对反演结果产生影响；2）连续入射角反演比单入射角可以利用更多的亮温信息。对2N 组SIC 结果根据各自的RMSE进行加权平均的方法可以在充分利用小角度亮温信息的同时，减轻小角度反演带来的误差，进而降低总体的反演误差；3）利用连续入射角组合S3的反演误差最低，在噪声为2 K 时，反演的海冰密集度的精度可以达到5%，但是在纯水区域会导致虚假海冰的浮现，需要后期优化算法对纯水区域进行校正。

本文初步证明利用连续入射角度差进行SIC 的反演的可行性。目前研究结果对于未来在89 GHz波段下，利用一维综合孔径微波辐射计扇形波束扫描成像或二维综合孔径辐射计的连续凝视成像，获取单个像元随多入射角的亮温分布并利用连续角度亮温差进行海冰密集度反演算法的研究和载荷设计具有一定的理论指导意义。

志 谢本文模型的输入数据由ECMWF 再分析数据（https：//www.ecmwf.int/）提供，模型验证数据由中国卫星气象中心网站（http：//www.nsmc.org.cn）提供，在此表示衷心的感谢！