地铁暗挖通道施工地层位移计算分析
程利民
(南昌轨道交通集团有限公司地铁项目管理分公司,江西 南昌 330000)
0 引言
近年来,在国家对基础设施建设的大力支持下,城市地铁建设蓬勃发展。在地下通道等工程施工过程中地层变形备受重视,并被严格监测,以防其对既有地下结构产生不利影响。为此,国内外许多学者对隧道开挖地层变形预测及控制开展了大量研究,并在地表沉降预测、控制技术等方面取得长足发展[1]。目前针对类矩形等异形截面隧道施工效应的室内模型试验研究还非常少见。张治国等[2]基于类矩形截面隧道开挖收敛位移模式,建立类矩形隧道开挖引起土体自由场位移的模型试验系统,通过模拟类矩形隧道开挖掘进过程,实时记录地表和地层内部的沉降变形,分析类矩形隧道开挖引起土体自由场位移分布与发展规律。安建永等[3]通过理论推导不同地层最大沉降位移与沉降槽宽度系数的函数关系和模型试验得到黏土地表以下不同深度地层沉降槽宽度系数的计算公式,从而为预测圆形隧道施工地表以下不同深度地层竖向位移提供了一种可靠的计算方法。以上研究已经对隧道开挖引起地层的沉降进行深入分析,但是未考虑因施工地层沿隧道纵向的水平位移,低估了地层沿隧道纵向剖面的变形程度。本文基于某地区地铁车站出入口暗挖通道工程,结合数值模拟及现场监测数据,考虑隧道施工引起的地层水平位移,在已有研究基础上进一步对地层水平位移计算公式进行了简单推导。
1 工程背景
本工程地下通道全长23.60m,在施工期间,坚持每日对地表沉降进行监测。开挖前在地下通道拱顶及两侧2m范围内采用WSS工法深孔注浆,防止拱顶下沉,并沿拱顶轮廓线打设超前小导管注浆加固。
1.1 工程地层地质
出入口暗挖通道工程范围内地层具有二元结构,主要以沉积物粗细变化显著的河流冲积层为主。地层岩性均表现出由上部黏性土逐渐过渡到下部非黏性土(砂土)的变化特点,岩土层自上而下逐渐变得密实,施工全范围内未见软弱层。
经现场勘探,按岩性及其工程特性,场地地层自上而下依次划分为填土层(杂填土、素填土),粉质黏土层,砂土层(中砂、粗砂、砾砂),风化泥质砂岩层(强风化泥质粉砂岩、中风化泥质粉砂岩)。根据地质时代、成因类型、分布范围及岩性特征自上而下分述如下:
(1)填土层:包括杂填土及素填土。杂填土土质较松散,全场地分布,灰色、灰褐色,干,主要由碎石、砂砾等组成。局部顶部0.3m为混凝土石块,稳定性和均匀性差。素填土土质较松散,全场地分布,棕褐、灰褐色,稍湿,主要由粉黏粒、砂砾及少量碎石组成。实测标贯平均锤击数为6击,稳定性和均匀性差。
(2)粉质黏土:全场地分布,褐黄、棕黄色,可~硬塑,成分以粉黏粒为主,刀切面较光滑,韧性中等,干,强度中等,中等压缩性,无摇震反应,实测标贯平均锤击数为11击。稳定性和均匀性较好。
(3)砂土层:包括中砂、粗砂及砾砂。中砂土质松散~稍密,全场地分布,棕黄、褐黄色,干~稍湿,松散-稍密,成分以石英、云母、长石及硅质岩等为主,粒径>0.25mm的含量约占60%。实测标贯平均锤击数为11击。稳定性和均匀性较差。粗砂土质稍密,全场地分布,棕黄、褐黄色,稍湿~饱和,稍密,成分以石英、云母、长石及硅质岩等为主,粒径>0.5mm的含量约占65%。实测标贯平均锤击数为15击。稳定性和均匀性较差。砾砂土质中密,全场地分布,褐黄、灰黄色,饱和,中密,成分以石英、云母、长石及硅质岩为主,粒径>2mm的含量约占40%。含个别卵石,磨圆度较好,呈圆状为主。修正后圆锥动力触探试验平均击数为10击,稳定性较好,均匀性较差。
(4)风化泥质砂岩层:包括强风化泥质粉砂岩及中风化泥质粉砂岩。强风化泥质粉砂岩全场地分布,紫红色,泥质结构,岩石风化强烈,节理裂隙发育,岩体破碎,岩芯呈碎块状及短柱状,碎块用手可掰断,正常钻进速度较快,岩芯采取率较低。属极软岩,岩石基本质量等级为Ⅴ级,修正后圆锥动力触探试验平均击数为11击,稳定性较差。中风化泥质粉砂岩全场地分布,紫红色,泥质结构,岩石风化中等,岩体较完整,局部见少许垂直裂隙,少数铁、锰质渲染,锤击声哑、无回弹、有凹痕、易击碎,岩芯多呈柱状或短柱状,属软岩岩石,基本质量等级为Ⅳ级。局部夹青灰色钙质泥岩,稳定性较好。
1.2 水文地质
根据区域水文地质条件及勘察查明,拟建场地地下水类型可分为上层滞水、松散岩类孔隙水、红色碎屑岩类裂隙溶隙水三种类型。暗挖通道结构施工过程中,开挖深度范围内不涉及到红色碎屑岩类裂隙溶隙水,且开挖几乎不受地下水影响,故不考虑地下水问题。
2 建立数值模型
如图1所示,运用有限元分析软件对某地区地铁车站出入口通道施工进行模拟。数值模型采用三维八节点六面体网格,为实现地下通道施工中地层深孔注浆、超前小导管注浆,在模型中对拱顶加固区域施加应力场,并在计算时通过改变场变量以达到加固的效果。数值模型计算涉及主要物理力学参数如表1所示。
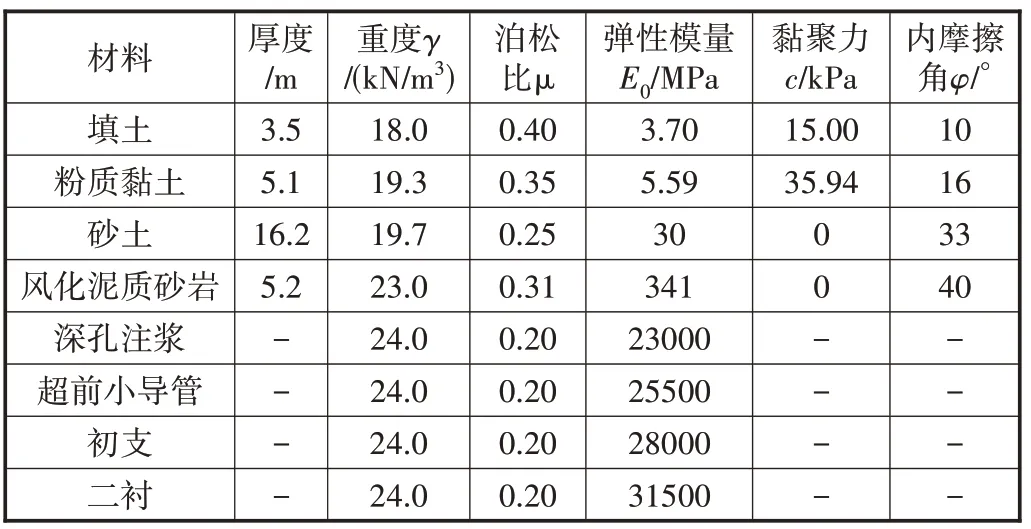
表1 数值模型主要物理参数

图1 数值模型
3 地层位移计算
自Peck[4]提出隧道开挖引起的地表横向沉降槽近似服从高斯分布以来,许多学者对地层变形特性进行了大量研究。其中,韩煊等[5]通过对国内多组隧道开挖地层沉降实测数据的分析,提出了地下沉降槽宽度计算修正公式,得到任意地层深度Z处沉降计算如下:
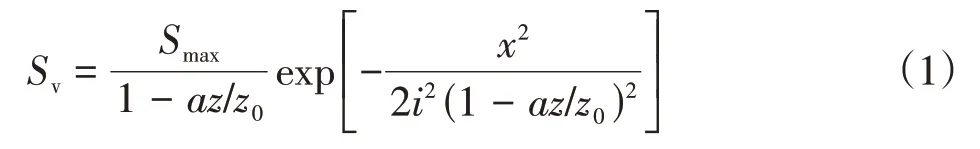
式中:
Smax——地面沉降的最大值;
z0——隧道深度;
a——不同地层类型的参数(对于黏性土,取0.65;对砂类土,取0.50);
x——沉降曲线中心到计算点的距离;
i——沉降曲线中心到曲线拐点的距离,称为“沉降槽宽度”。
公式(1)仅考虑到了地层任一点处的沉降特征,在实际工程中,变形不仅为地层沉降,还包括沿地下通道开挖方向的位移(下文称“水平位移”),地层的总变形量由沉降以及水平位移共同控制。如图2所示,现场监测值拟合曲线特征与数值模拟值变化特征基本一致,表明该数值模型可以反映实际工程情况,具有一定的代表性。

图2 地表沉降对比分析
为了分析地下通道开挖引起地层水平位移与沉降的关系,在(1)式的基础上引入比值系数k对距隧道轴线不同距离x处地层水平位移与对应沉降的关系进行拟合,二者关系如下:

根据数值模拟结果,因为地层变形以地下通道拱顶为界对称分布,地下通道拱顶剖面(x=0m)不同深度的沉降与水平位移的关系如图3所示,右侧地层各剖面(x=0~30m)沉降与水平位移的关系如表2所示。当x=(0~4)m时,随着距离增大,水平位移与沉降逐渐减小,比值系数k逐渐增大。

表2 水平位移与沉降比值表

图3 x=0m剖面沉降与水平位移关系曲线
地下通道开挖施工时引起的地层变形影响范围与其跨度密切相关,为了分析系数k与至轴线距离的变化规律,由表2绘制K值变化曲线,如图4所示。从图4中可以发现,k值随相对距离ξ(ξ=x/d,d为地下通道宽度)的增大而增大,其分布特征大致符合对数函数形式,在3ξ左右k值就已经无限趋近于1,但不会大于1(在距离无限远处,地层水平位移与沉降均为0,k=1)。利用Logistc函数对k值随相对距离ξ的变化特征进行拟合,得到k值拟合公式(式3):

图4 k值变化曲线示意图
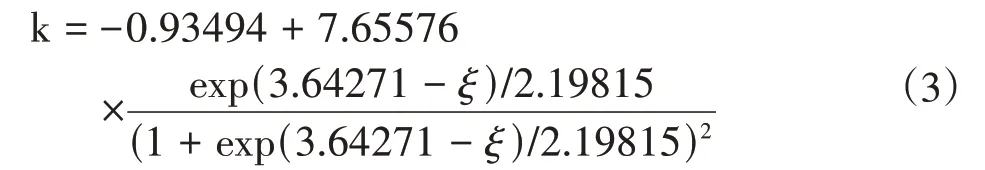
地层各点沿隧道纵向的总变形量计算公式为:

式(4)在地层沉降计算的基础上加入了地层水平位移,使计算结果更加贴近实际工程。根据上式特征,地下通道开挖引起地层位移变化曲线符合高斯分布特性,随着远离地下通道轴线,地层变形逐渐减小并趋近于零。
4 结束语
本文基于某地区地铁车站出入口暗挖工程,通过建立数值模型,结合现场监测数据对模型可信度进行验证,在韩煊等已有研究成果的基础上,对地层变形进行深入分析,提出包含地层水平与垂直位移的计算公式。通过此公式,能够更加准确地对地层位移进行分析,以便在实际工程中对地层变形进行严格把控,保证施工安全。
——以加拿大麦凯河油砂储集层为例

