路基同心筒发射导弹热环境与载荷特性对比研究
杨风波,周宏平,茹 煜,陈 青,成锋娜
(1.南京林业大学 林业资源高效加工利用协同创新中心, 南京 210037;2.南京林业大学 机械电子工程学院, 南京 210037)
1 引言
导弹主流发射方式有冷发射、热发射[1-2]2种,冷发射包括:燃气蒸汽式、燃气式[3-4];燃气式存在燃气烧蚀引起的热防护问题[5];燃气-蒸汽式设备庞大,常用于可提供较大空间的潜载发射平台。热发射包括:井式发射系统、同心筒[6-8]发射系统。虽然有冷发射系统采用低温药[9],但总体看,冷、热发射系统均会遇到显著的发射热安全问题。
鉴于此,发射领域的国内外学者致力于提升高温高速燃气流影响下的导弹热安全。其中,采用特殊结构和结构拓扑优化成为2种主流方向。姜毅等[10]进行了数值模拟工作和实验研究,提出了“引射同心筒”概念;马艳丽等[11]对“湿式同心筒”的降温效果进行了研究, 探索了用在筒底加水的方式来降低出口燃气温度;于勇等[12]利用拉瓦尔喷管加速的原理,提出一种外筒“变截面同心筒”;杨风波[8]分析了一种“中段导流同心筒”的发射热环境。
鉴于此,本文基于“中段导流”概念,针对“内圆外圆”、“内圆外方”2种路基同心筒;依托压力基的耦合格式对2种方案动态发射过程进行对比研究。在统一计算方法的基础上,从流场结构、参数分布的角度分别对压力基耦合格式进行了数值验证,最终对2种方案的导弹热环境、载荷特性进行了详细对比研究。
2 流场模型与数值计算方法
在理论计算中,对燃气和空气的性质及组分掺混做如下假设:1)燃气、空气为理想气体;2)燃气、空气参数取平均参数;3)多组分气体满足理想气体混合法则。多组分混合流满足质量守恒、动量守恒、能量守恒,对应的控制方程参考文献[7]。
使用有限体积法,对N-S方程组进行离散化,并使用压力基求解器进行计算,为保证计算的稳定性和收敛性,选用耦合格式进行迭代。在火箭发动机外场,高温高速燃气和空气发生掺混,气流速度存在高速区域和低速区域,故湍流模型采用既适用于高雷诺数,也适用于低雷诺数的RNGk-ε[13]模型。采用域动分层动网格技术对导弹运动引起的网格消失、生成进行处理,如图1、图2所示。

图1 网格消失示意图

图2 网格生成示意图
本小节首先验证耦合格式计算火箭发动机燃气射流纯气相流场的准确性。图3是火箭自由喷流任边界设置和参考文献[15]一致。oa段为燃烧室出口,设定为总压总温边界,abcde为燃设定为绝热粘性壁面,gh和hi为外流入口,采用远场边界条件,ij为压力出口边界,oj为轴对称边界。

图3 计算区域示意图
意子午面截得的一半区域,计算区域、网格设置、从图4中的(a)、(b)两图可以看出,文献[14]中三波点出现在离喷管轴线3.70 m处,本文中三波点出现在离喷管3.80 m处,相对误差为2.63%;文献[14]中,反射后,筒形激波和来流相交于轴线5.90 m左右,本文计算中,反射筒形激波和来流相交于轴线5.80 m左右,相对误差1.72%左右,表明耦合格式计算精度很高,和文献[15]采用的数值方法具有相当的计算精度,适用于燃气射流数值模拟。
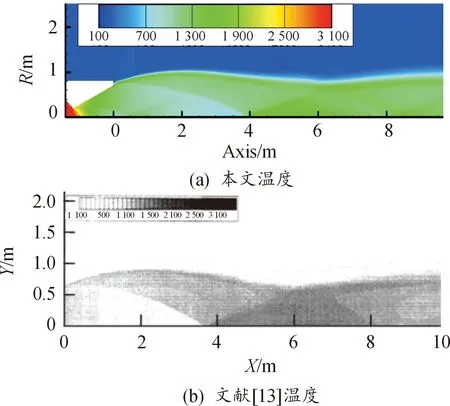
图4 本文结果与文献结果图
3 火箭注水气液两相流数值计算
3.1 2种方案的模型介绍
本文涉及到的中段导流同心筒结构2种:1、内圆外圆同心筒;2、内圆外方同心筒,如图5、6所示。同时,图5显示了内圆外圆同心筒方案的计算边界;图6为内圆外方同心筒方案法兰横截面结构示意图,从该图可以清晰的显示该方案的结构特点,圆内筒和方外筒通过若干筋板分割成若干腔室,且每个腔室横截面积不一致,其中对角线所在的四个腔室横截面积最大。

图5 计算边界示意图

图6 内圆外方同心筒在中段导流处的横截面示意图
图7(a)显示了待发射状态路基方案1;图7(b)给出了三维计算中域动分层动网格实现方案,采用分区的办法对各结构分别划分网格,并通过分层的方法(Interface1、Interface2、Interface3)实现区域的无缝整合,以实现动态计算;其中,在导弹底部区域伴随着网格的生成,在导弹顶部区域伴随着网格的消失,初始结构化网格数是265万。

图7 内圆外圆同心筒方案与网格示意图
图8(a)显示了路基方案2:底部有筒底挡流板结构和导流锥结构;发射装置内筒底部和外筒通过12条筋板连接,筋板一方面起连接作用,另一方面将燃气流规制到特定的区域,防止气流的窜动;中段导流以上的外筒和内筒直接组成一体结构,在中段导流板以上,已经没有名义上的内筒和外筒结构。观测面的高度和方案1一致,图8(b)给出了路基方案2的网格示意图,初始结构化网格数是285万。

图8 内圆外方同心筒结构方案与网格模型示意图
3.2 内圆外圆方案的动态数值计算
1) 流场结构:
为了确保三维网格模型的合理性,将方案一和二维轴对称计算进行了对比。图9显示了0.769 s时刻马赫数。从0.769 s时刻二维和三维计算马赫数的对比图可以看出,三维计算中yoz平面和xoz平面马赫盘位置几乎完全一致,说明该三维方案的流场特征呈现完全轴对称特性;对比二维计算和三维计算可以看出,2种计算吻合度良好,二维计算的马赫盘位置比三维计算稍微靠前,这可能是网格不一致,由于数值耗散引起的,误差几乎可以忽略不计;另外,中段导流板出口处z=3.9 m处的马赫数分布规律,可以看出,马赫数径向分布呈现良好对称性,计算效果较好。

图9 在0.769 s时刻二维三维计算马赫云图
2) 温度与载荷特性对比:
图10为观测面1的温度变化曲线(三维为相同高度均布0°、45°、90°的均值)。

图10 二维三维计算观测面1温度曲线
从图10中可以看出,二维和三维计算有一定的误差,二维计算温度幅值高出100 K左右,相对误差8.33%,可能是数值耗散引起的;另外三维计算的温度上升时间提前,温度下降时间延迟;0.2 s以内,三维和二维计算的观测面1温度对时间的积分值分别为:127.61 ( K·s),126.19 (K·s),吻合很好。图11为导弹载荷曲线,二维和三维模型中,导弹底部径向网格数为72和40,二维计算和三维计算得到的导弹过载吻合度非常好,二维计算值略高于三维计算值,相对误差不大于2%,二维径向网格更密,捕捉的合力脉动更为明显,但是两者的差异较小,说明三维计算对网格的敏感性要低于二维计算。总体上看,本文采用的三维计算的网格模型基本可靠。

图11 二维三维计算导弹载荷曲线
3.3 内圆外方方案的动态数值计算
按照方案1中三维结构化网格的尺度对模型2 进行建模,并进行动态计算。方案2横截面为长方形,且在内部布置12根筋板,导致发射装置每个腔室的几何很不规则,斜对角腔室、2个正交腔室截面积均不一样,斜对角最大,xoz面次之,yoz面最小,筒内的流场参数较为复杂。图12给出了在0.736 s时刻z=3 m的xoy平面发射筒内温度、压力和密度分布。

图12 在0.736 s时刻z=3 m的xoy切面物理量分布云图
从图12可以看出,温度分布差异不大;在对角线的4个腔室由于容积最大,对气流有引射与聚集作用,流进的燃气最多,密度要大于相邻腔室。图13给出了不同时刻不同高度xoy平面内压力分布规律,从图13可以看出,在0.736 s之后,燃气流流场结构基本稳定,对于图13(a)~13(c)中,斜对角腔室的压力值均大于相邻腔室的压力值,这是由于斜对角腔室容积最大,在同一时刻有更多的燃气流流进该腔室,使得其腔室密度更大、而温度比较接近(如图12)。另外,在同一时刻,随着离筒底高度的增加,对角线腔室压力呈现出“先增大,后减小”的规律。这是由于在对角线排气腔,导流锥折转的气流进入最多,在该腔室内部燃气排导不完全,所以在发射外筒中部出现了燃气聚集,压力稍微“增大”,在靠近中段导流板的部位,泄压较快,使得压力“减小”。此外,在同一时刻,随着离筒底高度的增加,yoz、xoz纵截面对应的腔室压力呈现“逐渐减小”的规律,总体来看,yoz、xoz纵截面对应腔室能实现燃气的较好排导。
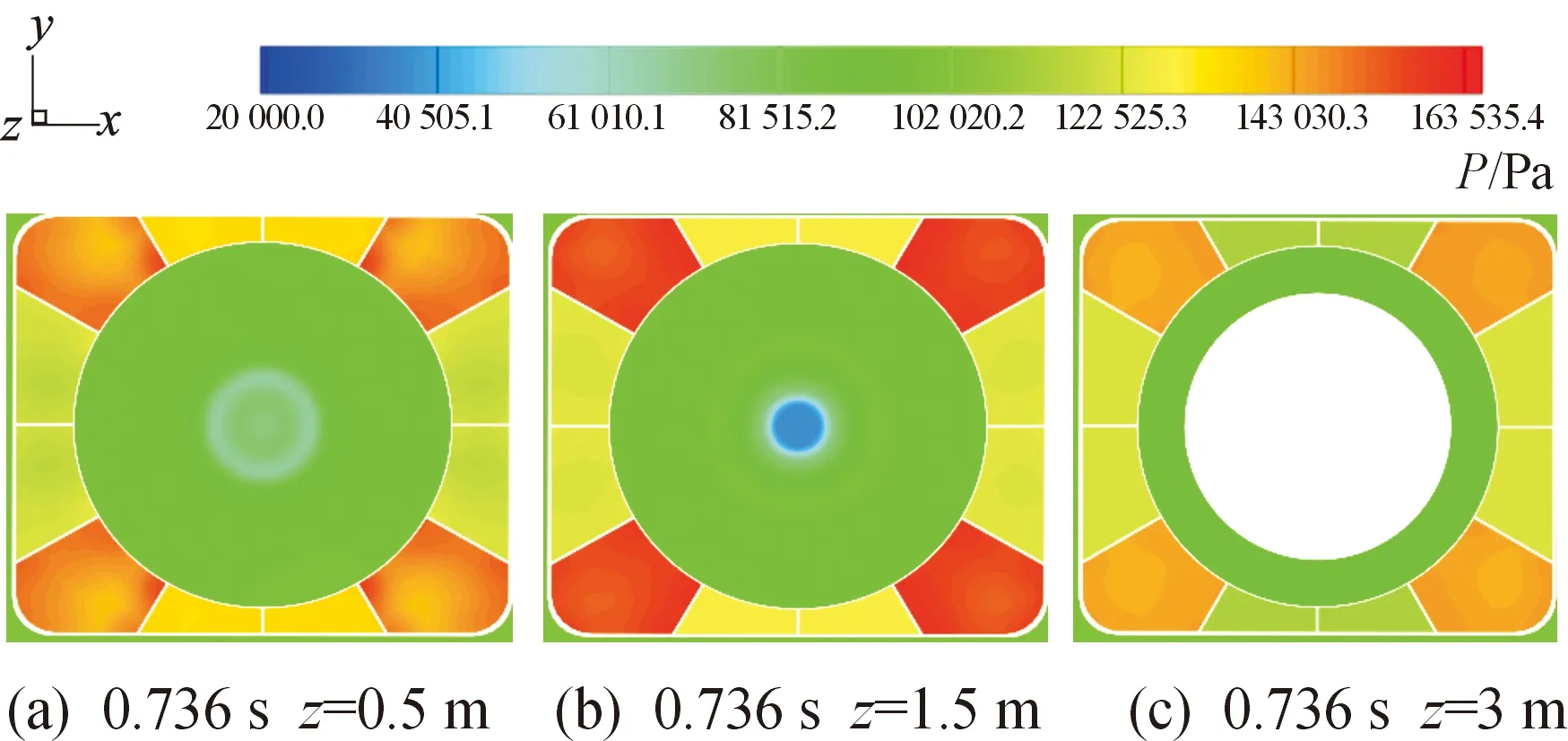
图13 典型时刻不同横截面静压力分布云图
图14给出了典型时刻不同截面马赫数分布规律,从图中可以看出,马赫数波节结构清晰,符合燃气射流马赫盘结构分布规律,表明本文的动态计算结果是可靠的。由于发射筒结构特殊,使得其流场结构呈现出特殊的现象,从图14中可以看出,在同一时刻,yoz面、xoz面和发射筒对角面对应不同的腔室呈现的马赫数的分布规律具有明显差异,yoz面和发射筒对角面“中段导流板”排导的气流马赫数几乎呈现水平射角,而xoz面排出的气流和“中段导流板”有一定的夹角,且随着导弹的运动,这个夹角有增大趋势。相对于yoz平面和对角线平面来讲,较小宽度的法兰对xoz平面的腔室排出的燃气规制导向作用有限,燃气排出后还要充分发展,所以该腔室排出的燃气和法兰呈现一定角度。
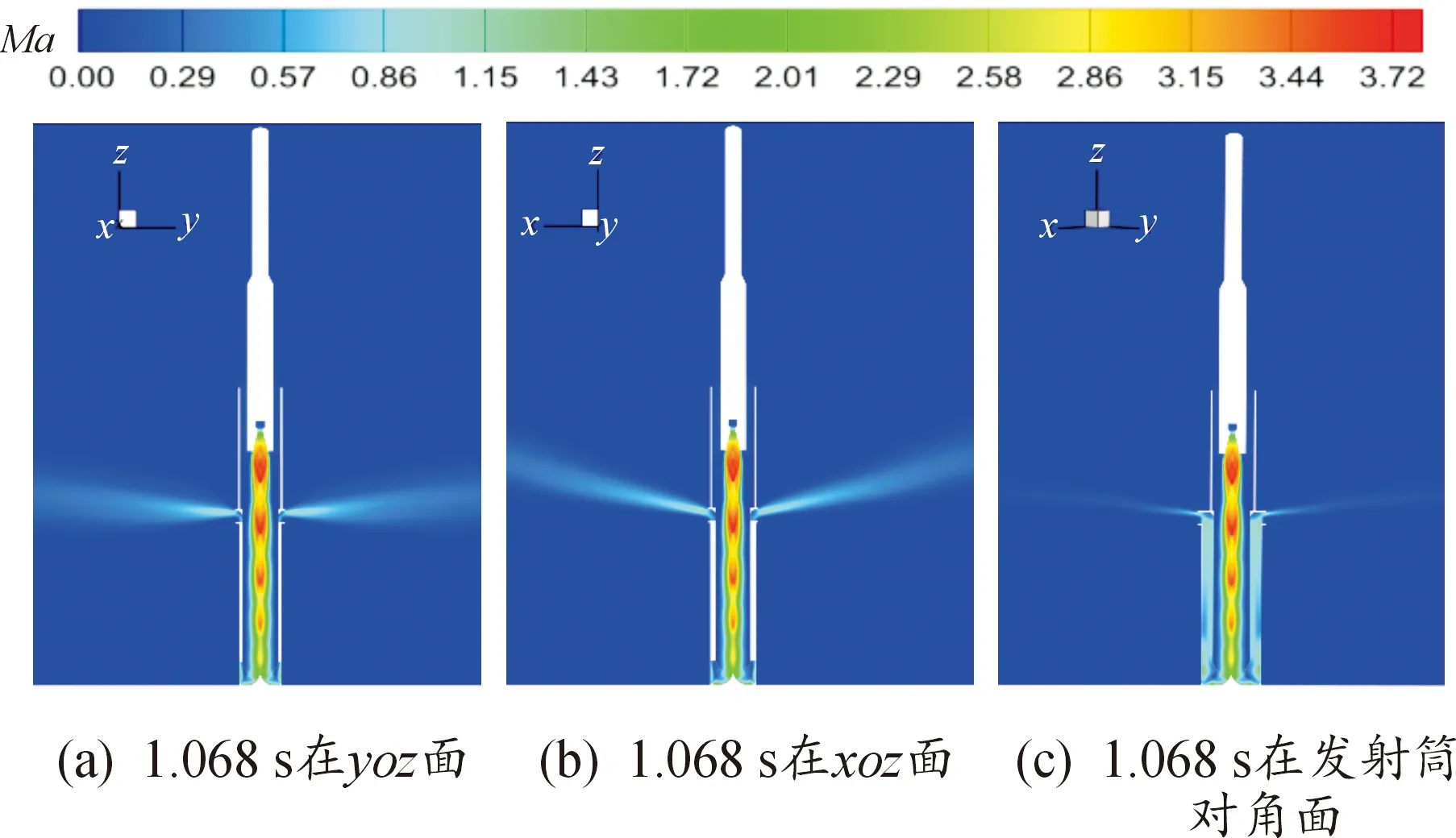
图14 典型时刻不同纵截面马赫数分布云图
图15为观测面1所在高度的导弹壁面 0°、45°、90°三个观测面的温度时间变化曲线。从图中可以看出,导弹观测面温度均呈现出“先上升、后下降,最后稳定在环境温度”的良好热环境特征,0.2 s以后导弹壁面温度降至环境温度,且没有温度的反弹;这和传统同心筒发射过程中,导弹被内外筒高温气流共同包束所导致其热环境恶劣的特征明显不同。但是,导弹底部仍然受到短时的高温燃气烧蚀作用,在xoy平面内,导弹0°、90°方向观测面温度基本趋于一致,最高温度达到2 930 K,45°方向导弹最高温度要低400~500 K左右,这是由于在45°方向对应截面积最大的腔室,呈对称分布,在燃气流迅速排导初期,45°方向腔室的空间最大,使得更多燃气流引射到该腔室,对内筒及导弹的影响就弱,弹道壁面温度就低。图16为导弹的过载曲线,总体来看,由于方案2同属于“中段导流同心筒”,受“引射效应”和“倒吸效应”的影响很小,导弹达到启动压力后,导弹的过载基本处于一个脉动稳定的过程。

图15 观测面1温度时程曲线

图16 导弹载荷时程曲线
3.4 2种方案热环境与载荷特性对比
总体来看,本文提出的2种发射装置都是“中段导流同心筒”的类别,但是不同的外筒结构使得发射过程中的热环境、导弹载荷特性不尽相同。总体来看,内外同心圆同心筒内导弹的热环境更优良,这可能是由于内外同心圆同心筒内部结构对称,流行性好,排导通畅,泄压及时所至;且由于内圆外方同心筒内部气流排导性能稍差,使得导弹底部的附加推力更大,进而导弹过载更大。具体如表1所示。

表1 2种方案温度与载荷
4 结论
1) 试验结果表明,将压力基耦合格式应用于计算火箭发动机超音速燃气射流可靠。
2) 内圆外圆、内圆外方2种同心筒发射三维动态计算表明:2种方案都具有“中段导流同心筒”的特点,受“引射效应”和“倒吸效应”的影响很小,导弹只在发射初期受高温燃气流扰动;内圆外方同心筒的特殊结构使得筒底排导性能稍弱,导弹热环境、载荷特性稍显恶劣;内圆外方同心筒虽方便路基运输,但结构还需进行多学科优化,使得技战术指标达到内圆外圆方案的同等水平。

