暗挖地铁隧道下穿既有道路的加固效果评估*

王英浩，王鹏超

（内蒙古科技大学 土木工程学院，内蒙古 包头 014010）

当新建地铁暗挖隧道下穿既有道路施工时，如果施工控制措施不到位，可能会导致地层产生变形，造成上覆道路的沉降开裂，特别是在软弱地层条件下进行施工时，为了有效预防和控制暗挖隧道下穿施工对既有道路产生的影响，一般都会采取相应加固手段对地层进行加固处理，以此减小施工风险.杨庆刚等[1]以南京4号线地铁隧道下穿江南水泥厂工程为背景，针对土体注浆加固前后、有无路基荷载、是否考虑路基荷载作用间歇性等情况下隧道施工引起的地表沉降及路基变形进行研究，采用数值模拟方法对现行施工方法进行了稳定与可靠性验证.黄合理[2]结合北京地铁7号线某区间隧道施工工程，利用经验法、分析法和数值模拟法预测了新建隧道穿越既有地铁车站引起的地表沉降，并提出以深孔注浆、小导管注浆等方式进行土体加固的建议，优化了施工方法与支护参数.张顶立等[3]结合厦门机场路隧道下穿地表复杂建筑群的工程实践，采用现场实测统计、数值模拟和理论分析方法，揭示了隧道施工影响下地表建筑物的变形规律、变形破坏模式.

贵阳市多山地、红黏土地质条件，大多地铁修建要进行山地条件下的隧道开挖，其不可避免地会下穿其他建筑物，施工存在较大风险.且目前贵阳地铁仅1号线开通运营，其他线路仍在规划或修建中，后续地铁工程建设量庞大.结合贵阳地铁2号线二期工程森龙暗挖隧道下穿龙水路区间段典型软弱地层施工实例进行分析，对地层进行地表注浆后的加固效果进行了评估，对本工程中相应地质条件下现行施工方法的可靠性进行了验证，本工程预测结果也可为贵阳地区后续类似工程的修建提供相应经验参考.

1 工程概况

1.1 工程简介

贵阳地铁2号线二期工程森龙暗挖隧道区间采用上下台阶法施工，部分区间段下穿既有市政道路龙水路，主要研究区间里程为DK43+025-DK43+075的高风险施工区段.本区间段下穿龙水路高填方地段，下层为抛填石块，上层为路基层，隧道洞身处于回填层之中，围岩稳定性极差，易出现坍塌和地表下沉风险，暗挖法施工开挖支护难度较大.经前期地质勘查发现道路路基下层为抛填石块与红黏土层，道路为在建状态.此段隧道埋深为7.45 m，隧底回填层最深7 m，两洞中线间距14.835 m，洞身主要位于抛填石块、红黏土层中，下覆基岩为中风化灰岩.此段隧道与道路位置关系如图1所示.

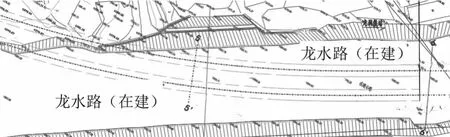
图1 隧道与道路位置关系图

1.2 工程地质条件

该段地表至隧道底部以下的地层依次为：①路基填石：杂色，石质成分以白云岩、灰岩为主，结构呈松散-稍密状态，层厚3～15 m，平均厚度10.16 m.②红黏土：褐黄色、褐红色等，可塑状，具有高孔隙比、高液限、高含水量、高饱和性、遇水软化、失水强烈收缩，裂隙发育、易剥落的工程性质，局部具弱膨胀性，层厚0.35～0.90 m.③中风化灰岩：灰白色、灰色，薄-中厚层状，隐晶结构，局部相变为泥质灰岩，岩体节理较发育，节理面多呈闭合型.钻孔岩芯呈短柱状、柱状及碎块状，节长5～20 m.此段工程受地下水影响甚微，地质剖里面图如图2所示.

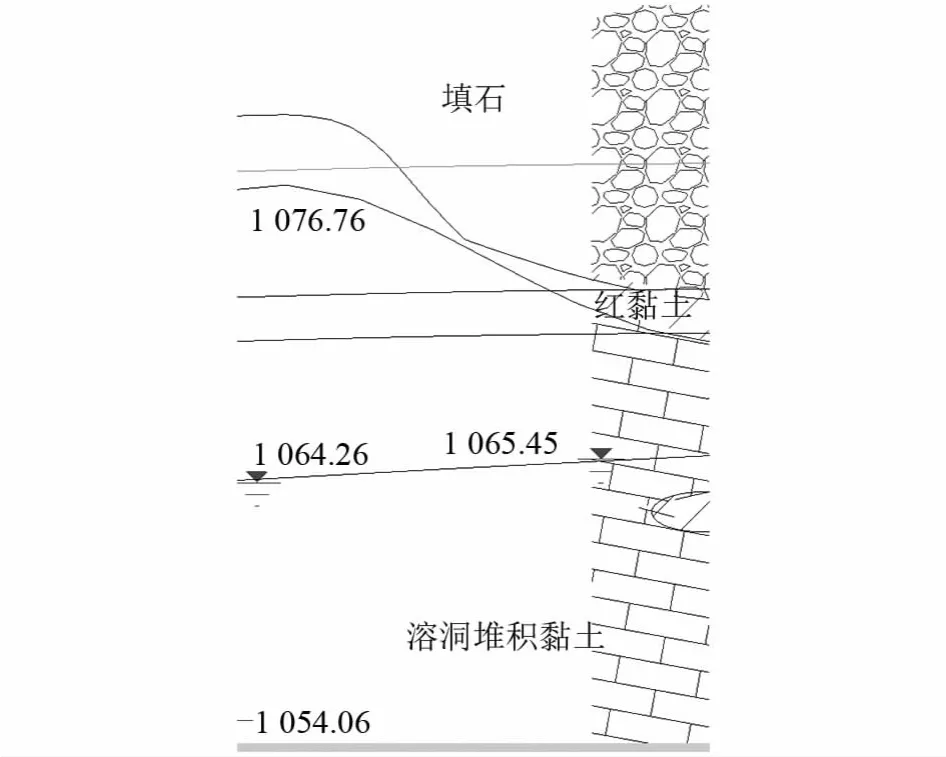
图2 工程地质剖面图（单位：m）

1.3 超前支护与施工工法

根据前期地质勘察结果，可知该场地地质条件较差，围岩等级为V级，极其不稳定，开挖时拱顶常伴有坍落现象，局部还有产生较大变形的可能.因此，该区间隧道施工以机械开挖为主，以减小扰动，仅对于部分坚硬部位辅以爆破破碎，同时加强支护.

由于台阶施工法能够有效控制开挖面稳定性和结构变形，抑制地层产生位移，且适用范围较广，施工空间较大和施工进度较快，能较早的闭合支护结构，结合本场地地质条件，本工程设计方案采用上下台阶法进行施工开挖，并严格控制超挖欠挖.隧道开挖后立即施作以锚杆、钢筋网喷射混凝土和钢拱架为主的初期支护，以缩短掌子面暴露时间，减小沉降，随后施作二次衬砌.并在隧道开挖前采用地表注浆方式对岩土体进行加固处理，在施工过程中实时进行沉降监测，利用现场监测数据反馈指导施工.隧道断面尺寸如图3所示，相关支护参数如表1所示.

表1 隧道支护参数

图3 隧道横断面

2 地表注浆加固效果分析

对于隧道开挖引起的地层变形，主要以地表沉降表现为主，为减小施工风险，需要对隧道即将开挖引起的地层沉降变形进行准确预测.文中将采用理论计算、数值模拟、实测数据分析相结合的方法对地表注浆前后的地层沉降变形进行预测研究，并对注浆加固效果进行评估，此结果也可为后续相关工程建设提供相应经验参考.

2.1 注浆前地表沉降变形理论预测

基于前期地质勘察结果，本工程开挖是在地表注浆加固后进行的，地表沉降变形实测数据也为地表注浆后施工监测所得，为详细评估地表注浆加固效果，现利用理论预测法对未进行地表注浆时地层的沉降变形值进行预测.

韩煊等[4]通过对我国多个地区实际监测的30多组实测数据进行统计分析发现，所得结果都能够较好地采用高斯分布进行拟合，并得出相应结论不论是黏性土还是砂砾石中的隧道开挖，盾构或浅埋暗挖开挖方法，亦或全断面法、台阶开挖法，其地表沉降曲线都基本符合高斯分布规律，这一结论明确了经典Peck公式在我国仍然基本适用.因此，可以充分利用国外数十年来在这方面积累的相关经验和数据，并尝试应用到我国的地铁建设当中.基于上述结论，对于本工程算例，采用Peck公式进行隧道开挖过程中地表沉降的预测[5]，公式如（1），（2）所示.

Peck公式：

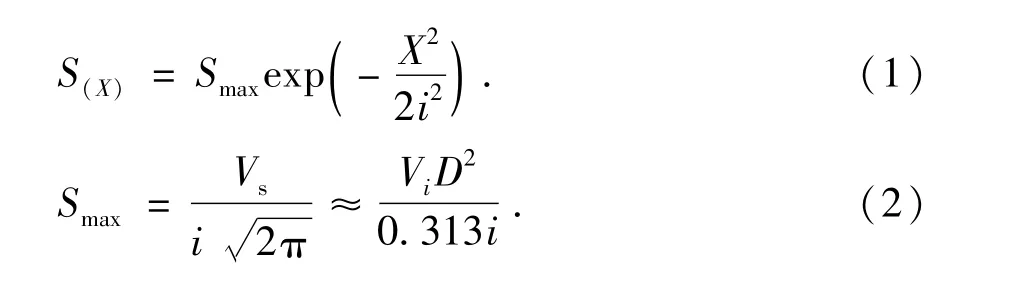
对于沉降槽宽度系数i的取值，根据Attewell等[6]人的研究，可以得到如下公式：

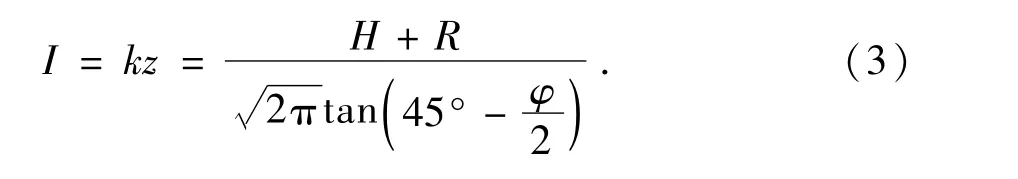
式中：K为沉降槽宽度参数，主要取决于地质条件；Z为隧道轴线到地面的垂直距离，m；H为隧道覆土厚度，m，取7.45 m；R为隧道等效半径，m，取3.435 m；φ为上覆土体平均内摩擦角，取15°

对于土体损失率Vi的取值，我国学者韩煊等搜集了广州、深圳、上海、北京、柳州、西北、香港、台湾等8个地区的30多组实测地表横向沉降槽的数据进行分析，给出了我国部分地区沉降槽宽度系数的初步建议值，根据其研究结果，并结合本工程前期地质勘察资料及邻近地区的经验参考，取Vi＝1.31%.

在确定好公式中各参数相应取值后，根据式（1），可以计算得到各断面沉降点的沉降值，具体计算结果如表2所示.

2.2 注浆前的地表沉降变形数值模拟

运用Midas／GTS有限元软件建立相应数值模型进行分析，先建立基础模型，后对基础模型中的相应条件参数进行调整以实现不同工况的模拟.基础模型隧道断面均为横向最大宽度6.62 m，隧道拱顶拱底间高度6.46 m的马蹄形断面.在水平方向上（X轴），模型的水平宽度取6.62×5×2+14.835＝81.035 m[7]（隧道中线左右两侧的水平宽度各取开挖隧道断面横向最大宽度的5倍，两隧道中线间距为14.835 m）；在竖直方向上（Z轴），模型底部距离隧道拱底距离取为洞高的3倍即6.46×3＝19.38 m[8]，同时隧道拱顶埋深为7.45 m；在隧道纵方向上（Y轴），模型的长度取为50 m.在模型正面、侧面、底面施加位移约束，在地表施加10.5 kN／m2的均布荷载模拟施加路面车辆荷载[9]，模型采用摩尔 库伦本构模型，3D混合网格进行网格划分，共包含49386个节点与86263个单元，模型示意图如图4所示.

图4 数值模拟模型示意图

2.2.1 计算参数选取

因为摩尔 库伦本构模型能较好的反映土体抗压强度不同的S-D效应，且简单实用，土体参数c，φ值可以通过各种不同的常规试验测定，较其他本构模型具有较好的可比性.结合本工程实际地质条件，文中岩土体数值模拟采用摩尔 库伦本构模型，隧道中其他衬砌及支护结构采用弹性本构模型，施工场地无地下水影响，各地层土体物理力学参数如表2所示.

表2 各岩土层的物理力学参数

2.2.2 数值模拟结果

现对注浆前隧道开挖地表沉降工况进行模拟，模拟施工方法为上下台阶法，上下台阶间距2 m，每次开挖进尺控制为1榀0.5 m，在每榀开挖完成后即进行初期支护.此段右线隧道开挖时左线隧道已开挖支护完成，左右线掌子面间距60 m，符合设计方案的左右线掌子面要错开5倍洞径距离要求.模拟地表沉降值如表3所示，数值模拟注浆前隧道开挖地表沉降位移云图如图5所示.

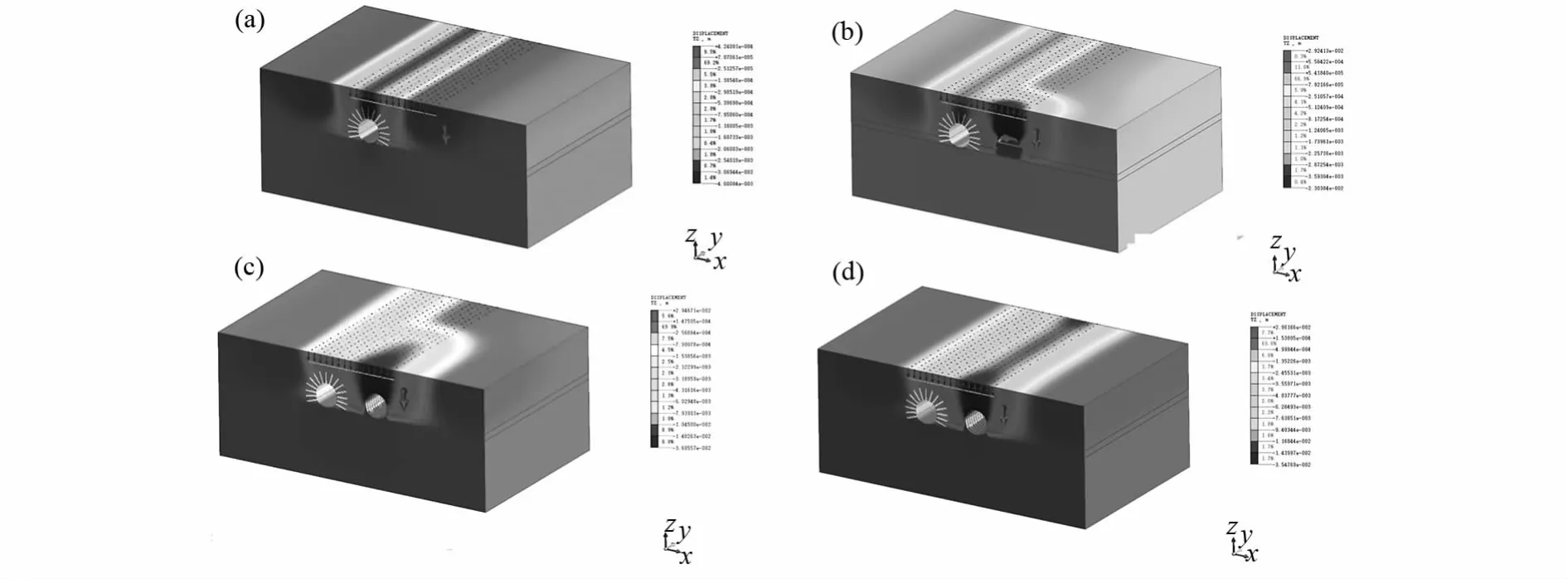
图5 注浆前隧道开挖地表沉降位移云图（a）注浆前右线隧道未开挖地表沉降位移，（b）注浆前右线隧道开挖一榀地表沉降位移（c）注浆前右线隧道开挖地表最大沉降位移，（d）注浆前隧道全部开挖完成地表沉降位移

在上述隧道支护条件下，理论预测法与数值模拟法的地表沉降值如表3所示.

表3 地表沉降理论计算与数值模拟结果对比

根据上文计算结果，可以看出在数值模拟左线隧道开挖支护完成后，左线地表最大沉降值只有4 mm，符合《城市轨道交通工程监测技术规范》[10]规范要求.当右线隧道开挖后，右线隧道地表开始产生沉降，待开挖至第49榀时，地表沉降量达到最大的35.476 mm.同时理论预测的地表最大沉降值也已经超过规范的30 mm要求，故应进行加固处理.理论预测与数值模拟结果对比如图6所示，可以看出理论预测与数值模拟地表沉降结果基本相近，沉降最大值相差5 mm左右，符合沉降预期.

图6 未注浆条件下数值模拟结果与理论预测结果对比

《城市轨道交通工程监测技术规范》中对于暗挖隧道区间施工最大允许沉降控制值为30 mm.以上两种预测方法得到的最大沉降量均超过30 mm，为了保证既有道路的安全，应加强对隧道的支护加固.

2.3 地表注浆加固模拟研究

基于上文计算结果，发现本工程在原始地层开挖条件下产生的地表沉降量过大，需对其进行加固，拟采用地表注浆方式对地层进行加固处理.注浆宽度范围为双线隧道结构最外侧左右各4 m，深度为基岩面以上至隧道拱顶以上3 m范围内.利用Midas／GTS软件对地层的注浆加固效果进行模拟研究，通过增大岩土体弹性模量的30%来模拟地表注浆加固状态[11]，数值模拟结果如表4所示.可以看出在进行地表注浆加固后，隧道上方地表最大沉降值为12.976 mm，较注浆前减小了22.5 mm，注浆前后各断面的沉降值对比如图7所示.

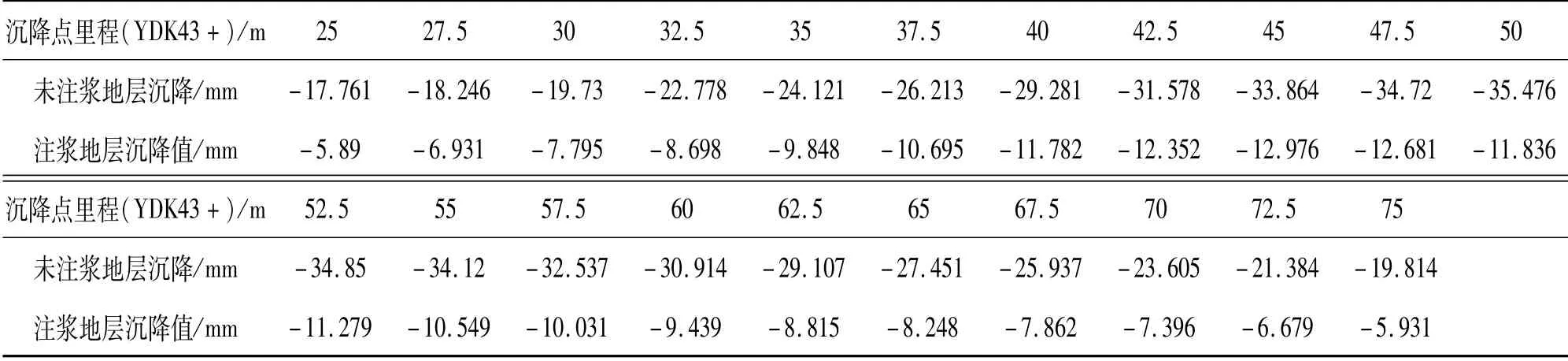
表4 地表注浆前后模拟沉降结果对比

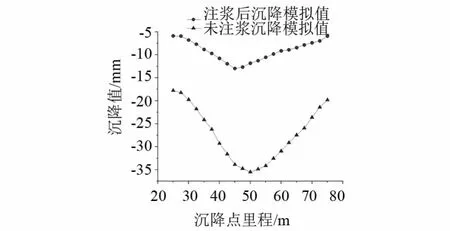
图7 地表注浆后与未注浆前沉降模拟值对比

根据模拟结果可得，注浆后的地表沉降值和模拟注浆前地表沉降值相比得到了明显减小，表明注浆加固对减小因隧道开挖引起的地表沉降变形效果明显，降低了破坏发生的可能性.数值模拟地表注浆加固后地表沉降位移云图如图8所示.

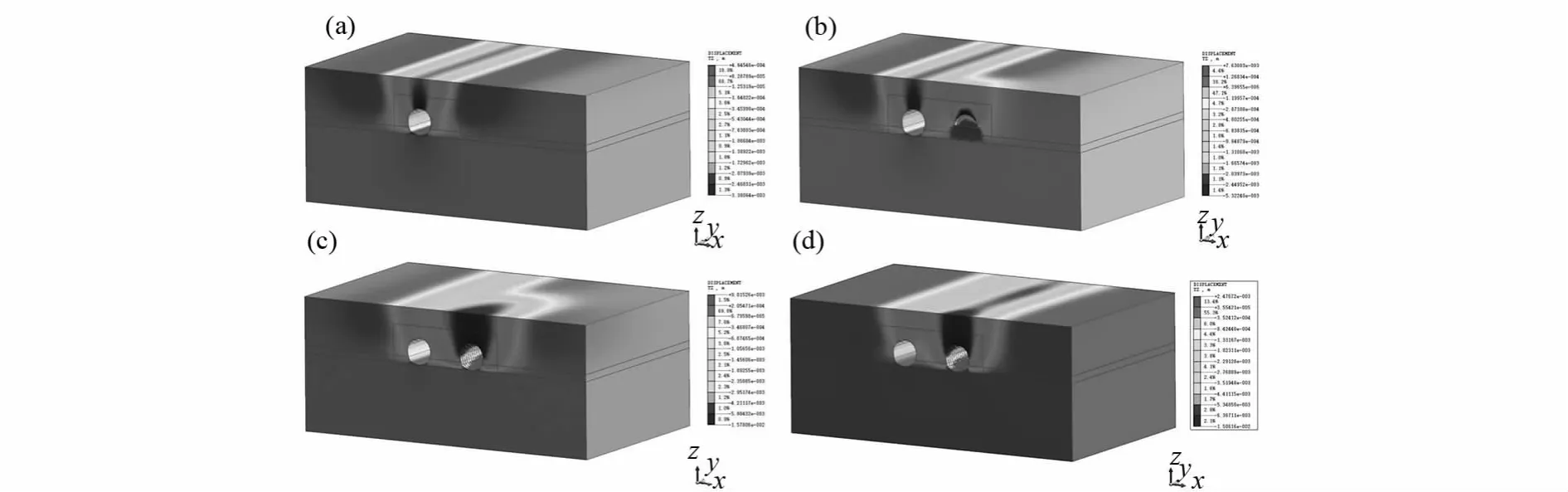
图8 注浆加固后地表演同降位移云图（a）注浆后右线隧道未开挖地表沉降位移；（b）注浆后右线隧道开挖一榀地表沉降位移（c）注浆后右线隧道开挖地表最大沉降位移；（d）注浆后隧道全部开挖完成地表沉降位移

2.4 实测数据分析整合与结果对比

在隧道进行地表注浆后的开挖过程中，实时对地表的沉降位移进行监测.地表沉降使用水准仪及配套铟瓦尺进行监测，参照标准水准点埋设方法，埋设2个临时水准基点，地表沉降观察断面设置为每个单洞口浅埋段各1个断面，测点按间距3 m布置.

将现场监测取得的各断面测点地表沉降最大值数据进行整合，绘制出沉降曲线如图9所示，可得最大地表沉降值出现在右线隧道上方的DK43+050断面测点处，最大地表沉降值为11.826 mm，符合《城市轨道交通工程监测技术规范》的相应沉降要求.由于现场施工条件和监测者技术水平的影响，会造成一定的监测结果误差，故需对数据进行拟合处理.利用Origin软件进行拟合，拟合收敛，沉降槽形状符合正态分布，判定系数R2＝0.78.

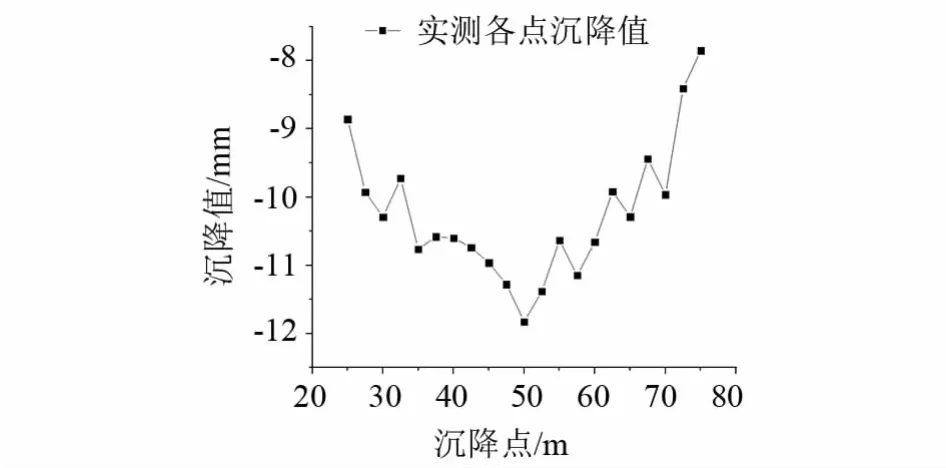
图9 隧道各点沉降实际监测值

通过现场监测结果与数值模拟结果的对比分析发现，数值模拟最大沉降点出现在右线隧道拱顶上方的DK43+045点处，沉降值为12.976 mm，数值模拟地表沉降曲线如图10所示.进行曲线拟合发现较实测数据拟合度有所提升，判定系数R2＝0.89.

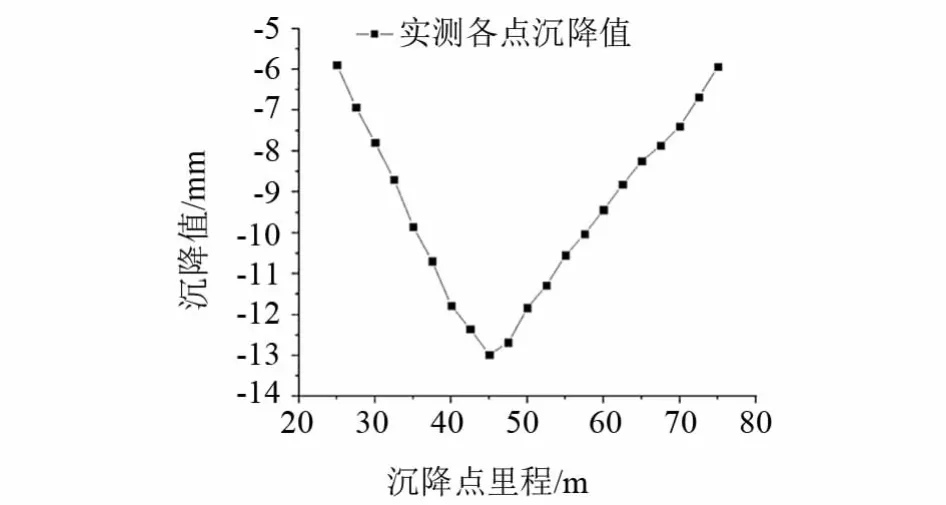
图10 隧道围岩注浆加固模拟沉降值

将整合后的实测数据与数值模拟结果进行对比，如图11所示.可以看出，数值模拟地表沉降值曲线与实测地表沉降值曲线形状略有差异，最大沉降差值为3.81 mm，最大沉降值断面测点间距5 m，沉降差均值为2.713 mm.因数值模拟采用最大风险条件进行工况模拟，故其沉降值偏大，现场实测值略小于数值模拟值.表明在现行施工条件下地表沉降得到了有效控制，验证了现行施工方法的可靠性.

图11 地表注浆沉降实测值与地表注浆模拟值对比

3 结论

1）本工程在未进行地表注浆条件下，用理论预测法和数值模拟法计算得到的隧道开挖引起的地表沉降量基本吻合，均表明隧道在不采取加固措施条件下进行开挖施工，引起的地表沉降位移和变形将会超过规范和设计要求的的最大允许值.

2）在进行地表注浆加固后，数值模拟的地表最大沉降量为12.976 mm，较注浆前减小了22.5 mm，减小比率达63%，注浆加固效果明显.通过与实测数据进行对比分析，发现两沉降值较为接近，说明数值模拟与实际较为贴合，数值模拟方法可为现场施工提供相应指导参考，为改进施工参数提供合理依据，所得结果也为后续相关工程建设提供了相应经验参考.

3）因隧道趋于最终稳定的时间较长，故对于隧道沉降、应力值变化等数据的监测周期也较长，此过程中应注意保持各个监测阶段的持续性，保证监测数据的完整性.加强对关键部位的监控量测，尽量减小人为监测误差，及时对数据进行误差分析，对异常数据予以纠正.