基于RBD的水下控制系统控制功能可靠性分析

尹 丰 文雨欣 陈 迪 牟雨言 岳元龙

（1.中海油研究总院有限责任公司，北京 100028；2.中国石油大学（北京），北京 102249）

0 引言

深水油气田环境复杂，操作风险高，开发难度极大。在生产过程中，一旦发生事故，将造成巨大损失。因此，在深水开发中，水下生产系统的长期可靠运行逐渐成为人们关注的焦点[1]，如何保证水下生产设施的安全性、可靠性显得尤为突出。而水下生产控制系统是水下生产系统的关键组成部分，承担控制各类水下设备操作的关键任务，一旦发生故障，将严重影响油气开采进度，造成重大经济损失。国内目前对水下生产控制系统的可靠性研究主要集中在单个设备上，对其完整的控制功能的可靠性尚未有深入研究。因此，研究水下生产控制系统控制功能的可靠性具有现实意义。可靠性框图（Reliability Block Diagram，RBD）是一种研究系统可靠性的重要方法，该方法用框图的形式表示大型复杂系统中各个组成部分的可靠性逻辑关系，常见的可靠性逻辑有串联连接、并联连接、混合连接以及复杂的网络系统等。该文以某实际油气田为研究对象，创新性地以开启PMV和CIV为例对其水下生产控制系统的控制功能进行链路划分，根据链路划分形成的可靠性框图进行可靠性分析。

1 水下控制功能链路

为了对水下控制模块、水下仪表以及液压动力单元等单体设备的集成功能进行可靠性分析，验证控制系统能否安全执行控制功能，该文提出“功能链路”概念，对控制信号经过的设备进行划分，形成功能链路。并以功能链路为基础，对由各条链路所组成的控制系统整体的可靠性进行分析。

复合电液控制是目前水下控制系统的主流控制方式，该系统执行控制功能时需要的设备包括主控站（MCS）、电力单元（EPU）、液压动力单元（HPU）、水上脐带缆终端（TUTA）、静态脐带缆、水下脐带缆终端（SUTA）、水下分配单元（SDU）和水下控制模块（SCM）[2]。控制功能实现的原理如下：由MCS将控制信号发给EPU，在EPU内的调制解调器里将控制信号叠加在电力波上，控制信号以电力载波的形式进行信号传输。将电力载波信号和HPU发出的液压信号线路共同送至TUTA，从TUTA出发，通过1根脐带缆输送至SDU。SDU将控制信号、电力信号、液压信号以及化学药剂信号分别输送至水下采油树上的SCM里，最终实现控制水下设备的功能。

其中，SCM作为水下生产控制系统的核心设备，根据水上主控站的控制指令控制水下生产设备上各种执行器的开启和关闭。因此，当划分控制功能链路时，要单独将SCM链路细化到板卡级别。

绘制水下控制系统控制功能链路，如图1所示。其中，PMV控制功能链路只由控制信号链路和液压供油链路组成，共同控制PMV阀门开启或关闭；CIV控制功能链路由控制信号链路、液压供油链路和化学药剂链路组成，共同控制CIV阀门开启或关闭。

2 功能链路可靠性计算方法

可靠性框图可以通过框图将系统内元件功能层面的逻辑关系表现出来[3]，说明组件的可靠性如何影响复杂系统的成功和失效，一般用于大型复杂系统，是一种效果非常好的可靠性分析工具。该文介绍的链路存在串、并联特点，采用可靠性框图法根据水下生产控制系统开启PMV和CIV的逻辑关系建立可靠性模型。水下生产控制系统设备的可靠度计算方法如公式（1）所示。

式中：Ri（t）为某设备的可靠度；λi为设备的失效率；t为工作时间。

通过可靠性框图的方法建立控制PMV和CIV开启链路上各部件的相互关系，即串联或并联，从而计算系统的可靠度。

当部件串联时，系统中任一单元出现故障都会影响系统的正常运行，串联系统的可靠度如公式（2）所示。

当部件并联且系统所有单元都故障时，才会影响系统的正常运行，并联系统的可靠度如公式（3）所示。

当部件交叉连接时，难以分割为串联或并联形式，可以采用下面的方法进行可靠性建模分析，交叉连接形式如图2所示。

当对复杂系统进行可靠性计算时，采用最小路集法。最小路集是指当系统能正常工作时，从输入端到输出端连接的所有弧的集合，如果删去其中任何一个弧就不是路集。可以通过输入端到输出端的最小路集综合运算得到复杂系统的可靠性，如公式（4）所示。

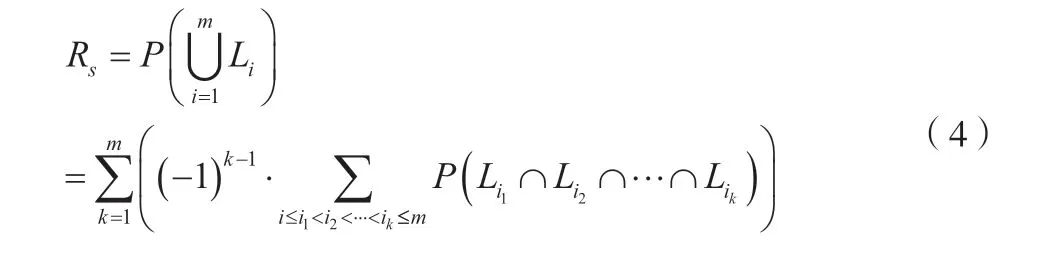
式中：m为路集个数；P（Li）为路集的可靠性参数。

在系统模型（图2）中，最小路集共4个：L4为AB，L2为AD，L3为CB，L4为CD。由公式（4）可以求得系统的可靠性。

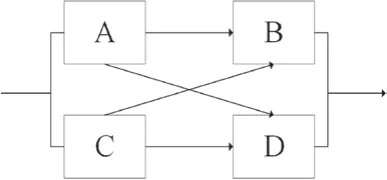
图2 交叉系统模型

3 水下控制功能链路的可靠性建模

3.1 PMV控制功能链路可靠性建模

根据功能链路划分结果可知，当水下控制系统控制PMV时，需要控制信号和液压油的共用作用，只有这2条链路同时可靠，才能开启阀门。因此，当用可靠性框图进行建模时，这2条链路之间是串联的逻辑关系，需要分开计算后再求得整个PMV控制功能链路的可靠度。

3.1.1 控制信号链路可靠性框图建模

控制信号链路可靠性框图如图3所示。首先，根据公式（4）计算图3中SCM内交叉冗余部分的可靠度。其次，根据串并联逻辑算法计算控制信号链路的可靠度。采用MATLAB绘制可靠度曲线，时间t=10 a 。

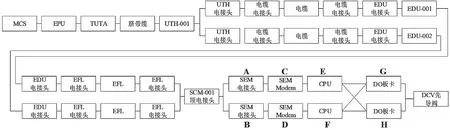
图3 控制信号链路可靠性框图

在MATLAB中绘制交叉冗余部分可靠度随时间变化，如图4（a）所示。由曲线可知，交叉冗余结构的可靠度很高，系统运行10 a后的可靠度还能保持在99.97%。在交叉冗余部分可靠度已知的情况下，根据可靠性框图串并联算法计算控制信号链路的可靠度。可靠度曲线如图4（b）所示，系统运行10 a后控制信号链路的可靠度大约降至98%。

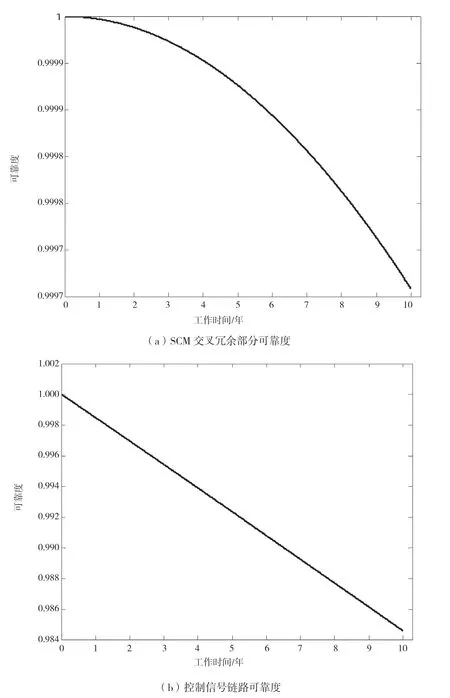
图4 可靠度曲线

3.1.2 液压供油链路可靠性框图建模

液压链路可靠性框图为串联逻辑关系，根据功能链路里液压供油传递路径建立可靠性框图模型如图5所示。

根据图5用串联算法计算液压链路可靠度后，串联液压链路与控制信号链路求得控制PMV控制功能链路的可靠度，绘制控制PMV的整条功能链路可靠度曲线，如图6所示。

图5 液压链路可靠性框图

由图6可知，采用划分功能链路的方法可以对水下控制系统功能进行可靠性分析。随着时间的增长，水下控制系统对PMV的控制功能可靠度随之降低，实际工程应用中要求水下控制系统的可靠度大于或等于98%，建模结果显示系统运行10 a后，控制功能可靠度大约降至97%，因此可以在可靠度降低至98%时进行检修和维护工作，以维持可靠性。

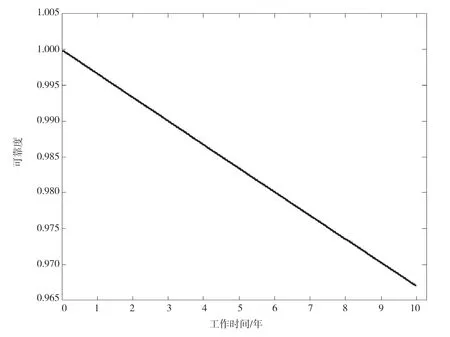
图6 PMV控制功能链路可靠度

3.2 CIV控制功能链路可靠性建模

根据功能链路划分结果可知，当控制CIV时，需要控制信号、液压油和化学药剂的共同作用，只有这3条链路同时可靠，才能开启阀门。因此，当用可靠性框图建模时，这3条链路之间是串联的逻辑关系，需要分开计算后再求得整个控制功能链路的可靠度。

其中，控制信号链路和液压供油链路已在3.1中计算过，只需要对化学药剂链路进行建模，再与上述2条链路串联即可得到CIV控制功能链路可靠度曲线，化学药剂链路可靠性框图如图7所示。

图7 化学药剂链路可靠性框图

绘制CIV控制功能功能链路可靠度曲线，如图8所示。由图8可知，采用划分功能链路的方法可以对水下控制系统功能进行可靠性分析。随着时间的增长，水下控制系统针对CIV的控制功能的可靠度随之降低，实际工程应用中要求水下控制系统可靠度大于或等于98%，CIV控制功能链路在系统运行5 a后的可靠性就大约降至98%，因此，应在此时进行检修和维护，以维护可靠度保持在要求的范围内。

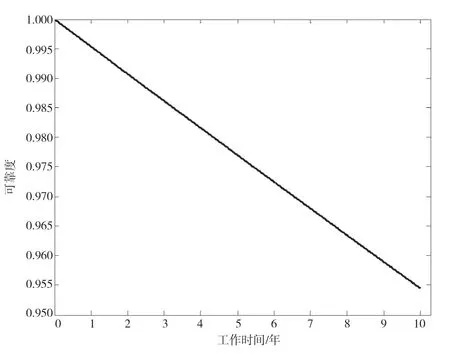
图8 CIV控制功能链路可靠度

4 结语

针对2种不同类型的水下控制系统控制功能，以功能链路为基础，利用可靠性框图建立相应的可靠性模型，根据链路中设备及部件的串联、并联或交叉连接结构对水下控制系统的控制功能进行可靠性分析，得到以下3条结论与建议：1） 根据对交叉冗余结构、控制信号链路、液压供油链路和化学药剂链路可靠性建模分析结果可知，交叉冗余结构和并联冗余结构可以提高系统的可靠度，而串联结构越多，系统可靠性会越低。在运行期间需要缩短系统检修和维护周期，以达到系统的可靠度要求。2） 采用绘制功能链路图的方法可以更清晰、有效地对水下控制系统某控制功能进行可靠性计算和分析，以衡量该功能的可靠度。3） 采用可靠性框图法对功能链路进行建模，可以高效地计算链路的可靠度，还可以通过改变PMV和CIV控制功能链路的配置、增加交叉冗余结构对链路进行修改，用可靠性较高的组件替换可靠性较低的组件，实现优化功能链路的目标。重新计算链路可靠度，对比优化前后的计算结果，为水下控制系统设计决策提供参考。