微小卫星太阳翼铰链展开过程同轴问题研究
韩玮杰 尉瑞江 盆洪民 冯利明 孟庆昕
(天津航天机电设备研究所,天津 300457)
0 引言
微小卫星具有功能密度高、技术发展快、研制周期短、开发成本低以及部署应用灵活等特点[1],受到世界主要航天大国的重视,同时也被许多中、小发达国家和新兴的发展中国家作为发展小卫星技术的切入口[2]。
由于受运载空间的限制,因此太阳电池翼在发射前全部是以折叠形式存放在整流罩中的。为了保证太阳翼顺利展开,国内外对太阳翼铰链设计、铰链装配技术等方面进行了大量研究。
国外对太阳翼铰链机构的研究起步相对较早,自20世纪60年代,国外的许多机构和公司都对太阳电池翼铰链机构进行了大量系统的研究,并研制出多种类型的一次或多次机械式铰链机构[3],且已具有相当成熟的技术。国内主要参照国外的成功案例进行研究设计,对铰链展开过程的同轴度的研究较少。
通过模拟分析2018年、2019年某型号微小卫星入轨后延迟问题发现,太阳翼铰链的同轴度会严重影响太阳翼的顺利展开。因此,该文对保证太阳翼顺利展开的铰链同轴度进行研究。
1 太阳翼展开机构铰链自由转动同轴度理论分析
1.1 同轴度分析
为了方便说明同一侧铰链同轴度对转动的影响,将上侧铰链暂定为A铰链,下侧铰链暂定为B铰链,如图1所示。
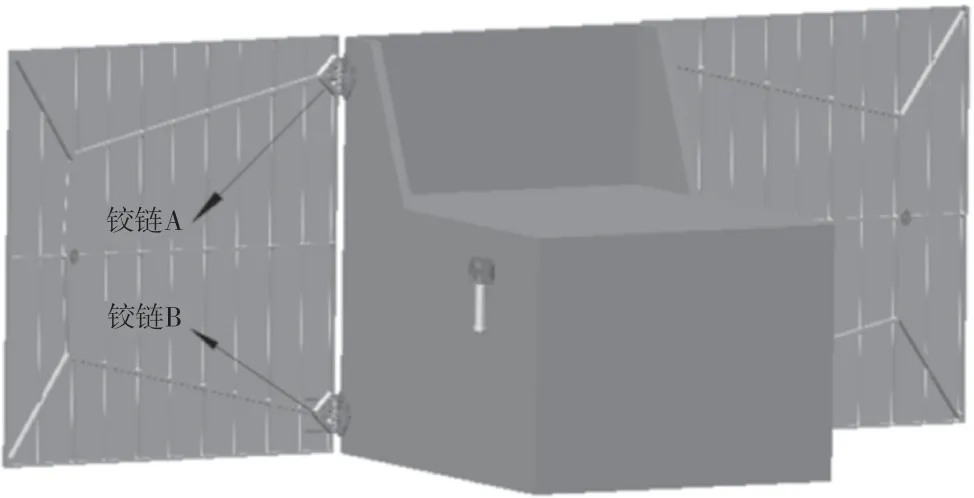
图1 微小卫星太阳翼铰链
转动轴在固定铰和转动铰中是间隙配合的,转动轴会在固定铰中沿垂直太阳翼固定铰安装面的方向平行移动或相对固定铰转轴安装孔轴线转动。同时,转动铰也会相对转动轴平行移动或相对固定铰转轴安装孔轴线转动。当平行移动时,对同轴度的要求最高,因此分析平行移动时A铰链和B铰链的同轴度。以A铰链为例,根据铰链组件零件配合尺寸图(图2)(固定铰孔径ø7 mm(0,+0.022),转动铰孔径ø7 mm(+0.05,+0.025),转动轴轴径ø7 mm(-0.005,-0.02))的配合关系可知,当转动轴与固定铰装配时,转动轴与固定铰轴孔单边最小间隙为0.002 5 mm;当转动轴与转动铰装配时,转动轴与转动铰轴孔单边最小间隙为0.015 0 mm。
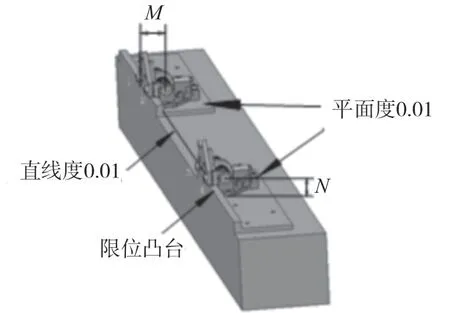
图2 铰链组件装配
由于转动轴与固定铰配合孔之间的间隙为微米级,因此假定转动轴与固定铰无相对运动,则转动铰配合孔相对转动轴的轴向单边最小间隙为0.015 mm,即A铰链在转动轴与转动铰同轴度为ø0.03 mm的范围内可以灵活转动;同理,B铰链在转动轴与转动铰同轴度为ø0.03 mm的范围内也可以灵活转动。
以A铰链为装配基准,为了保证B铰链装配完成后2套铰链能灵活转动,就必须保证装配完成后2套铰链的同轴度满足各自的转动区域且转动区域有重合,如果没有重合,就会出现2套铰链卡死的情况,太阳翼基板无法顺利展开,只有当2套铰链各自转动轴与转动铰之间的单边间隙小于或等于0.03 mm时,才可以实现A铰链、B铰链的同时转动,即2套(A铰链、B铰链)铰链自由转动时同轴度须小于或等于ø0.06 mm。
为了保证太阳翼基板顺利展开,就需要保证太阳翼机构2套铰链的同轴度满足精度要求。在实际铰链装配过程中,为了使铰链同轴度量化,采用控制2套铰链同轴度在上述ø0.06 mm圆的内接四边形范围内变化的方法,即通过2套铰链水平方向偏差ΔM和竖直方向偏差ΔN来保证2套铰链的同轴度。
1.2 展开最大同步距离
对2套铰链同轴度的影响分为A、B铰链固定铰尺寸的偏差和装配过程的偏差。最恶劣情况为ΔM=ΔN且满足同轴度小于或等于ø0.06 mm,即2套转轴在水平方向偏差和竖直方向偏差不超过0.02 mm。要保证恶劣情况下的同轴度,就需要通过工艺措施来控制2套铰链中的固定铰的转轴孔距底面和侧边的距离精度,从而控制2套铰链轴孔对同一基准的距离偏差,使其满足同轴度小于或等于ø0.06 mm的需求。
该文把保证太阳翼正常展开的2套铰链转轴的最大同轴度值称为展开最大同步距离。
2 太阳翼铰链装配
为了保证太阳翼铰链通过一次装配就满足同轴度的要求,设计了保证同轴度的工艺装备,并在完成太阳翼铰链的装配工作后,对太阳翼的展开力矩进行测试,验证太阳翼的展开性能是否良好,确保在轨顺利展开。
2.1 太阳翼展开机构铰链展开最大同步距离验证
为保证A、B铰链的同轴度满足要求,在装配过程中,要求工艺装备固定铰安装面的2个凸台面的平面度优于0.01 mm,凸台左侧的靠面直线度优于0.01 mm,最外侧的工艺装备边缘相对凸台靠面的平行度优于0.01 mm。分别实测2组铰链轴线到工装边缘水平距离M和竖直高度N,竖直水平距离各取4点,计算得到最大偏差ΔM、ΔN,验证是否满足公式(1)。

分别测量N1、N2、N3、N4、M1、M2、M3和M4,取△Nmax与△Mmax带入公式(1),如果满足,那么2套铰链的同轴度满足展开最大同步距离的要求,2套铰链在转动过程无卡制。
该文分别对地面试验装配、力学试验前整星装配、力学试验后整星装配以及发射场整星装配4个过程中太阳翼同轴度进行研究。
每次装配前,先将铰链A和铰链B安装在同轴度测试工艺装备上,实测N1、N2、N3、N4、M1、M2、M3和M4,M值理论尺寸为8.5 mm,N值理论尺寸为14.5 mm,实测结果见表1~表4。

表1 M值与N值实测值(地面试验装配)(单位:mm)

表2 M值与N值实测值(力学试验前整星装配)(单位:mm)

表3 M值与N值实测值(力学试验后整星装配)(单位:mm)

表4 M值与N值实测值(发射场整星装配)(单位:mm)
2.1.1 地面试验装配
△Mmax=0.01,△Nmax=0。将数值
带入公式(1),得到0.02<0.06,2套铰链同轴度满足展开最大同步距离的要求。
2.1.2 力学试验前整星装配
△Mmax=0,△Nmax=0.01。将数值带入公式(1),得到0.02<0.06,2套铰链同轴度满足展开最大同步距离的要求。
2.1.3 力学试验后整星装配
△Mmax=0.01,△Nmax=0。将数值带入公式(1),得到0.02<0.06,2套铰链同轴度满足展开最大同步距离的要求。
2.1.4 发射场整星装配
△Mmax=0.01,△Nmax=0。将数值带入公式(1),得到0.02<0.06。
从上述计算结果可以看出,4次太阳翼装配后的2套铰链同轴度均满足展开最大同步距离的要求。
2.2 铰链装配后转动功能验证
每次调试好2套铰链的同轴度后,将太阳翼与铰链A、铰链B安装好,拆除同轴度调节工装,将带有铰链的太阳翼安装在太阳翼展开力矩测试的工艺装备上,验证铰链A与铰链B的装配满足转动要求,测试太阳翼展开和收拢过程中的力矩,如果转动过程无卡滞,展开力矩无明显波动并在理论值范围内,就证明太阳翼可以在轨顺利展开。
在展开力矩测试过程中,需要保证拉力方向垂直于太阳翼基板,通过移动平台匀速拉动拉力计,拉动方向与太阳翼展开或收拢方向一致,并记录拉力计的最大读数。
分别在3个位置(30 °、60 °和90 °)测试太阳翼的力矩。在每个位置对太阳翼施加外力矩M1和M2,使太阳翼分别在展开方向和收拢方向达到静力平衡状态,即可通过M1和M2计算得到展开力矩和摩擦阻力矩。太阳翼通过展收试验得到的展开力矩和摩擦阻矩如图3所示。
在图3中,还分别展示了太阳翼在4个不同阶段装配后实测的进程刚度曲线和回程刚度曲线。在4张图片中,太阳翼的进程刚度与回程刚度的一致性很好。通过进程刚度与回程刚度的关系计算得到摩擦阻矩,摩擦阻矩随太阳翼展开有变小的趋势,与摩擦阻矩设计值变化趋势一致,说明太阳翼装配可靠,精度满足要求,展开过程顺利无卡制。
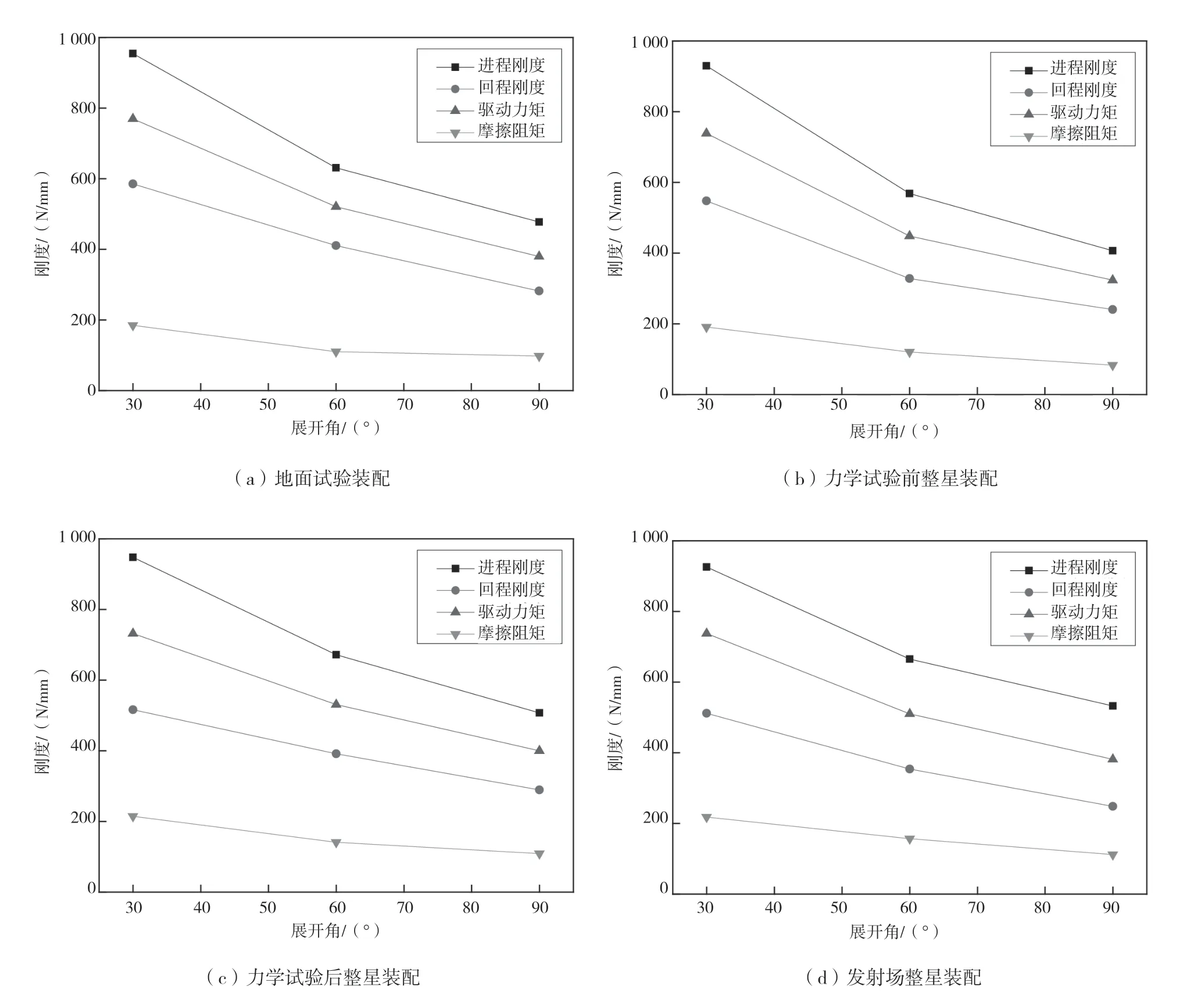
图3 展开力矩与摩擦阻矩变化曲线
3 结语
针对微小卫星太阳翼在轨无法顺利展开的问题,该文以典型的微小卫星太阳翼铰链为例,对保证太阳翼铰链同轴度的条件进行研究,给出了保证太阳翼顺利展开的同轴度公差范围的计算方法,提出了展开最大同步距离的概念,通过理论推导得出了该距离的计算公式。同时,在该理论的基础上,设计了保证同轴度的工艺装备,并在该基础上对微小卫星太阳翼装配技术进行研究,通过展开试验验证了该理论和装配方法的可行性和有效性,提出双轴甚至多轴太阳翼的装配方法,为后续提高太阳翼装配工艺技术提供了理论依据。并且,该装配工艺方法已成功应用到2颗卫星太阳翼铰链的装配中,太阳翼在轨顺利展开。该太阳翼装配技术使太阳翼的装配一次完成,减少了反复调整太阳翼、铰链与卫星之间的装配关系的次数,节省了装配时间,提高了太阳翼装配工艺技术,满足了后续微小卫星太阳翼批量化生产的需求,适应了航天产业快速发展的需要。根据该理论和方法还可以为多轴铰链太阳翼机械部分结构提出改进建议。

