一种基于数据融合的目标跟踪方法

顾保国，陈 阳

(1.中国人民解放军63726部队，银川 750004；2.华东电子工程研究所，合肥 230088)

航天测控技术发展日新月异，目标跟踪作为航天测控核心功能之一，也相应地越来越复杂。在目标跟踪应用中，单个传感器(单套设备)跟踪目标有一定的局限性[1]，为了获取更好的跟踪效果，常常会利用多个传感器(多套设备)输出的测量数据[2]，以实现目标跟踪精度和收敛性的进一步优化[3]。在测控任务中，利用雷达、光学设备等多种外部设备的测量数据来引导相控阵波束进行目标跟踪，以期达到更好的跟踪效果，相关文献研究表明，组网雷达系统的检测与跟踪性能比单部雷达显著提升[4-6]。

通常，测控设备接收到的引导数据受到网络或环境影响，经常出现数据跳大数或时延抖动，同时在过顶跟踪时受到引导信息动态滞后等因素影响，因此有必要将多设备源发送的引导数据结合自跟踪获得的测量信息，进行数据融合处理。数据融合可以利用多个或多种体制的传感器所提供的冗余信息和互补信息[7]，从而提高融合后目标信息的质量[8]，减少测量信息的模糊性和不确定性，避免因自身自跟踪或外部引导数据出现的各种异常造成对目标预测影响，提高目标的跟踪能力[9]。但传统的数据融合方式是根据经验对各种测量数据赋予固定的权值，不能准确反映外部引导数据质量的变化，虽然在一定程度上提高了目标跟踪能力，但仍然存在比较大的跟踪误差。为了提高相控阵雷达波束的跟踪性能，笔者提出一种基于多源数据融合的目标跟踪方法，将各数据源输入的引导数据通过外推时延修正、检择处理、野值剔除、坐标变换、平滑滤波后，实时根据测量方差进行权值的自适应动态分配，预测目标下一周期的俯仰角和方位角，并引导跟踪波束进行波束切换，从而完成相控阵波束的目标跟踪，仿真实验结果表明，所提算法相对于传统的跟踪算法，显著提高了波束的跟踪预测性能，增强了系统的可观测性和可靠性。

1 数据预处理

1.1 处理流程

图1描述了多源数据融合的数据处理流程图。整个处理流程采取“分布式预测+集中式融合”架构，计算系统通过网络或串口接收各数据源的数据，然后开启多个线程对各数据源的引导数据进行外推时延修正、数据检择、坐标变换(将各自坐标系转换到地心地固坐标系)、平滑滤波。将滤波后的估计结果加上自身设备的自跟踪预测值传送到数据融合模块，完成数据融合，并输出最终的融合结果来引导波束进行跟踪。

图1 多源数据融合处理流程图Fig. 1 Flow chart of multi-source data fusion processing

1.2 外推时延修正

由于各数据源的测量值是在各自的时间基准下进行的，再加上网络或者串口的传输时延，汇聚到计算平台的各数据源的测量数据和计算平台本地时间必然存在一定的时间差，并且由于UDP传输过程偶尔会造成网络丢包，造成测量数据丢失或中断，因此各种引导数据的测量时序是异步的。为了使得各数据源数据在融合之前具备统一的时间基准，需要对各数据源所测量的异步数据同步到同一处理时间节点上。数据外推时延修正是进行数据融合处理的前提，其处理精度关系到后续目标的捕获跟踪连续性[10]。由于不同的外部所发送引导数据频率不统一，有的设备频率较高，有的设备频率较低，通常情况下，通过线性插值(或线性外推)将一方配准到另一方的观测时刻，时间配准原则是将数据率较低的一方配准到数据率较高的一方。令Tr为待处理的时间节点，Ar为待处理时间节点观测异步数据的数据项。Ti，Ti+1为待处理时间节点最邻近的2个时间节点，Ai，Ai+1为待处理时间节点最邻近的2个时间节点所对应的数据项，按式(1)对其进行内插或外推时间配准处理，保证待融合的数据时间间隔相等。

(1)

1.3 数据检择

各数据源的引导数据会存在一定的野值数据，需要对引导数据的相关测量数据进行数据检择处理，保证后续处理精度。利用最小二乘法对测量数据进行预报，通过与相应的测量值进行对比，将测量数据残差与预先确定的野值检测门限做对比并进行检测。大于所设置检测门限的测量值判定为野值。

数据检择模型采用四阶差分检验法进行检验[11]，步骤如下

1)用四阶差分检验法式(2)对初始的五帧数据进行初始检验，找出一组合理点

Δ4yj=yj-4-4yj-3+6yj-2-4yj-1+yj(j≥5)，

(2)

取门限值M1(经验值为17σ，σ为测量数据的精度)，判断|Δ4yj|≤M1是否成立，若是，则认为这5帧数据无异常点；否则，令j=j+1继续进行四阶差分检验。

(3)

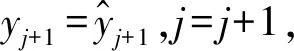
图2以外部引导数据的俯仰角度为例，展现了数据检择的效果。可以看出数据检择能将测量过程中的几个跳点很好地剔除，和原始数据相比也保证了检择处理后数据基本在真实数据附近，避免了异常值引入带来的风险。

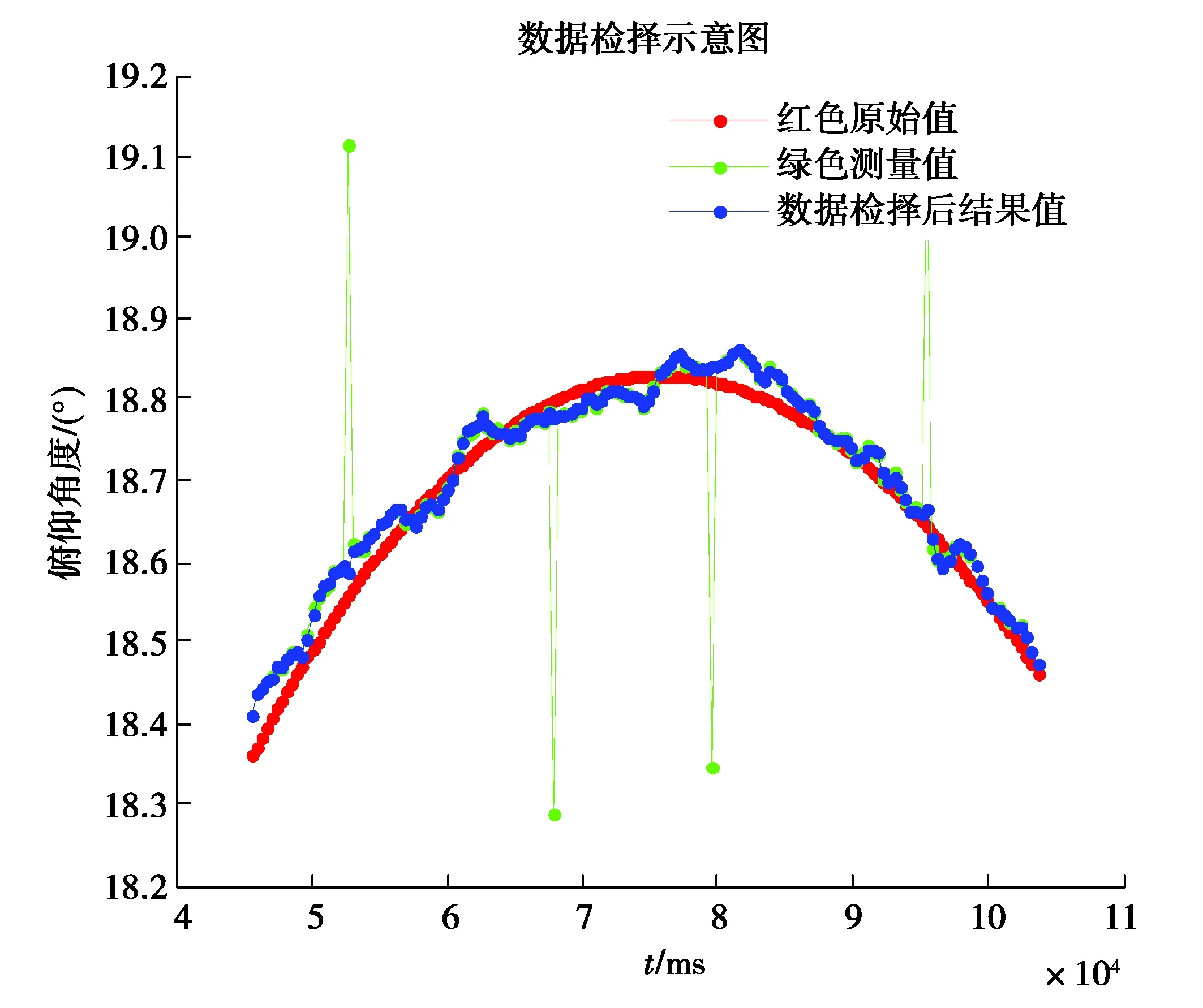
图2 数据检择效果图Fig. 2 Effect chart of data selection

1.4 坐标变换

由于外测设备传送的数据是在地心坐标系下的位置或者是经度、纬度和高程，比较特殊额的是同站设备，它的引导数据是测站系下的位置，而自跟踪数据是阵面坐标系下的测量值。同一波束指向通常是相对于阵面坐标系的，为了描述同一个目标的位置属性，保证融合坐标系的统一，需将目标观测数据转换到同一坐标系、同一量测单位[12]，即阵面坐标系。坐标转换如图3所示。如果是运动平台，则要将平台的位置姿态信息(经度、纬度和高程)先转换地心地固坐标系，再转化到东北天坐标系获得姿态角。地心地固坐标系下的目标位置结合姿态角转换到平台坐标系下的位置，再转化到阵面坐标系下的位置和极坐标下的角度。如果引导数据是经度、纬度和高程信息，则要先转化地心地固坐标系。

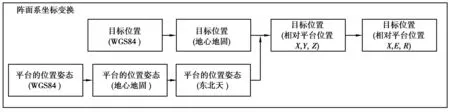
图3 坐标转化图Fig. 3 Coordinate transformation diagram

1.5 平滑滤波

经过上述坐标转化后获得目标在阵面坐标系下的方位角和俯仰角测量值的离散点序列yi。为了保证测量值的平滑性，采用七点3次平滑法[13]的 式(4)对采集到的测量数据进行离散值平滑。

(4)

如果数据源事先知道其轨迹位置，则可以根据式(4)平滑7个时刻点的方位角和俯仰角，然后将其送入数据融合模块和自跟踪数据进行融合处理；如果数据源为实时发送的数据，则刚开始的7点利用原始值进行融合，后面的数据则利用式(5)根据平滑后的值进行外推。

(5)

其中η1+η2+η3+η4+η5+η6=1。通常离最新引导数据最近的点对于预测贡献值较大，所以取η1>η2>η3>η4>η5>η6。

2 数据融合

通过数据融合，有效利用不同数据中的信息，可提高目标跟踪精度[14]。由于目标的真实运动轨迹未知，将各数据源的引导数据、自跟踪数据的测量信息的中心点看作目标真实运动轨迹的参考点，各测量信息与参考点的偏差看作是目标运动轨迹的偏差。利用统计理论计算出各测量信息与参考点偏差的标准差,这里之所以不用平均偏差而用标准差，是因为平均偏差给出的平均值比实际平均偏差大[15]。以标准差作为数据融合精度近似,并以该近似值分别计算出数据融合加权平均合成时各测量信息的权值。

假设在数据融合时刻Ti，经数据预处理得到的引导数据或自跟踪数据中的方位角/俯仰角信息为Ai,m，m为数据源的数量。则数据融合时刻Ti的测量方程为[16]

Ai,m=Xi,m+Vi,m，

(6)

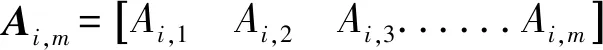
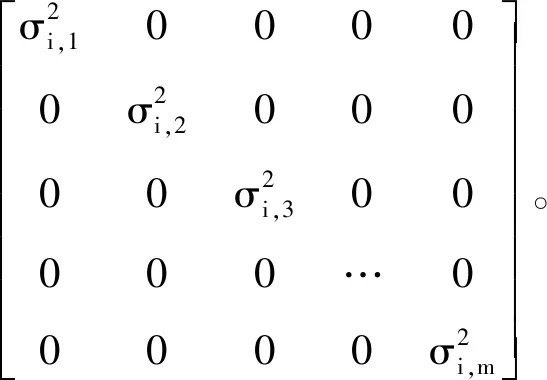
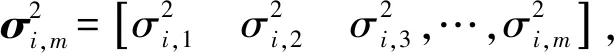
建立加权估计误差方差表达式[17]

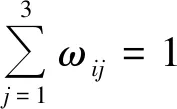
依次对加权因子求取偏导，联立求解可得

在Ti时刻，确认是对同一目标的测量数据，可利用加权最小二乘估计进行合成[18]。输出Ti数据联合处理后的目标测量数据。

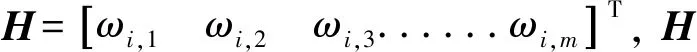
3 仿真分析与实验

3.1 精度对比

利用仿真实验验证了目标跟踪方法的正确性。以3种数据源作为输入，包括引导数据1(测站坐标系下测量数据)、引导数据2(地心大地坐标系下测量数据)和自跟预测值，数据采样周期1次/s。经过融合后的目标俯仰角跟踪结果如图4所示。从结果可以看出，融合后的俯仰角和真实的角度几乎重合，而自跟预测值和真实值之间误差大于融合后的误差，融合跟踪与真实值的偏差较自跟预测值与真实值的偏差降低了80%以上。这说明单一利用引导数据源1或数据源2，或自跟踪预测值，对目标的跟踪精度显著低于融合后的跟踪精度。图5为提出的方法与文献[10]所提出方法的比较也验证了所提出的融合方法的有效性。

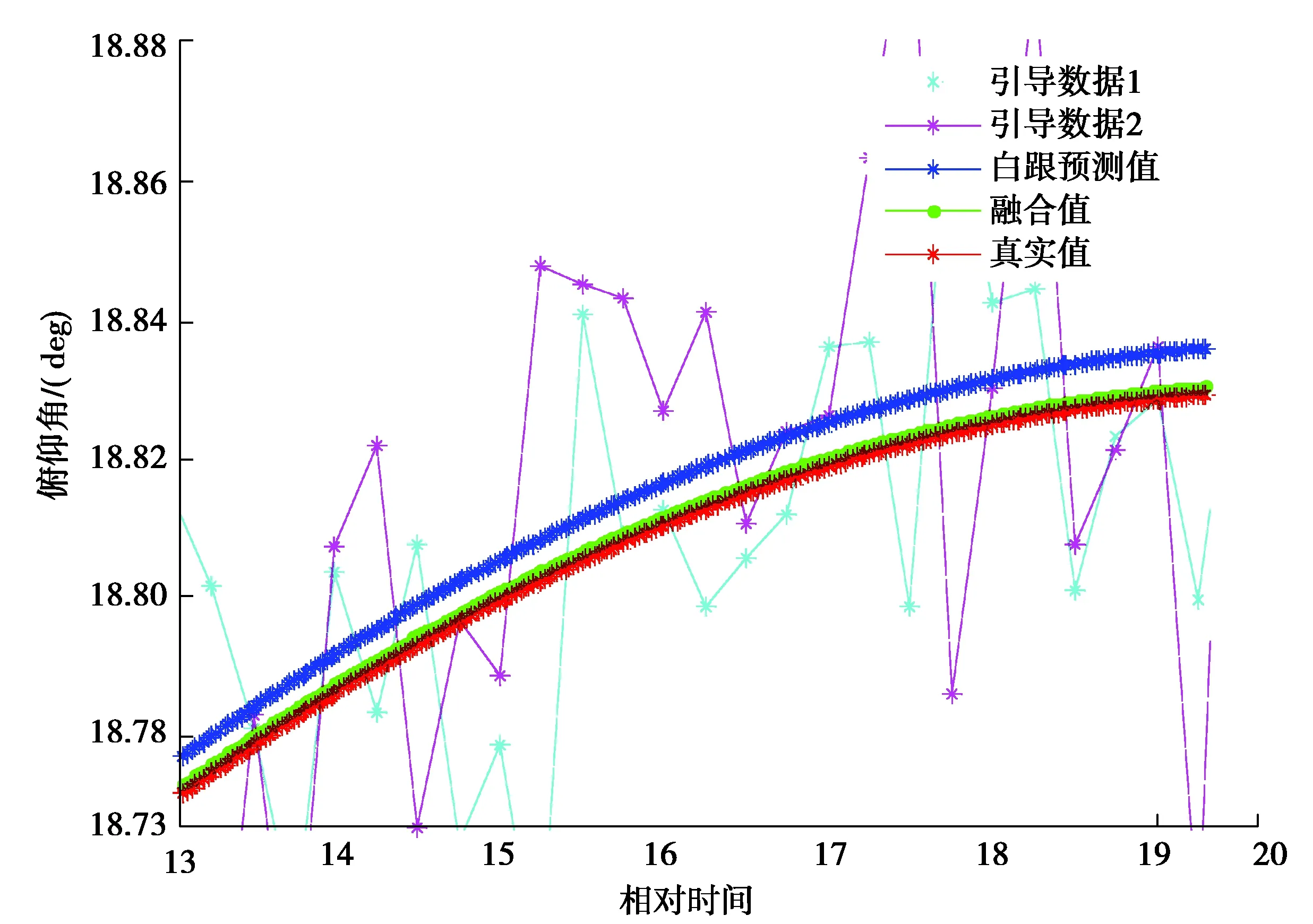
图4 研究方法的跟踪结果图Fig. 4 Tracking results of the method in this paper

图5 与文献[10]的方法比较Fig. 5 Comparison with the method in reference [10]

3.2 时间代价对比

将所提出的算法与文献[10]中的方法以及未采用融合跟踪处理的算法进行对比，选取同样一组数据(100帧)作为输入数据，在同样软硬件环境下进行仿真运算，3种算法的运算耗时分别为1.125 ms、0.013 ms和0.002 ms，虽然算法耗时远高于另外2种(分别是另外2种算法的86倍和562倍)，但仍然远小于跟踪与伺服控制计算机的主线程周期(主线程周期一般12.5 ms，即80 Hz)，不会对天线的跟踪控制造成任何不利影响，完全可以接受。

4 结 论

为了解决目标在相控阵波束下的有效跟踪的问题，利用多设备源采集的引导数据、自跟踪数据的测量信息，进行数据融合处理，提出了一种基于动态权值分配的数据融合跟踪方法。与传统的仅利用自跟踪数据进行目标波束跟踪相比，所提方法在付出时间代价可接受的情况下有效提高了仅依赖单一设备源的数据的跟踪精度，值得注意的是，讨论数据融合的目标跟踪方法是基于多设备源均能获取相应的测量信息，在实际的目标波束有效跟踪工程实现时，将该方法作为目标波束有效跟踪输出的一种策略。实际策略自适应切换所应满足的条件，将是下一步重点研究的内容。