混合永磁游标电机磁链观测器设计与协调控制方法
包广清,祁武刚,b,c
(兰州理工大学 a.电气工程与信息工程学院;b.甘肃省工业工程先进控制重点实验室;c.电气与控制工程国家级试验教学示范中心,兰州 730050)
随着电气、液压、机械以及控制等相关学科的飞速发展,顶驱钻井系统(top-driving drilling system,TDS)已成为钻采装备的主流机型。国内传统TDS大多数采用异步电机加齿轮箱的传动机构,但有关数据表明,超过40%故障来自齿轮箱机械故障,且维护保养成本高[1]。基于永磁同步电机(permanent magnet synchronous machine,PMSM)的直驱式TDS系统,由于不需要配备额外的齿轮变速机构,系统可靠性得到提升[2]。然而,为了满足TDS低速大转矩要求,采用普通PMSM的槽数及永磁体极数较多,导致TDS装备体积笨重庞大,机组运维成本依旧居高不下。
近年来,基于“磁齿轮效应”的磁场调制电机引起了工业界和学术界的广泛关注。其中,永磁游标电机(permanent magnet vernier machine,PMVM)由于具有“自减速”和高功率密度的特点,可以省去齿轮箱等复杂传动链,实现了无齿传动,从而避免传动磨损和漏油等因素所造成的机械故障,并且降低噪音污染,有效提升工作效率、机械稳定性和使用寿命。TDS全速域、多工况应用背景要求顶驱电机系统能够实现大范围高效平滑调速,然而基于磁性能较为稳定的高矫顽力永磁体(high coercive force, HCF)电机气隙磁场难以调节,PMVM电机弱磁范围有限。同时弱磁控制会增加电机铜耗,导致系统效率下降,还可能造成不可逆退磁的风险[3]。因此,在PMVM中引入低矫顽力永磁体(low coercive force, LCF),构成混合永磁游标电机,既可以保证电机的力能指标,又能够根据工况需求实时调节气隙磁场,实现电机的高转矩输出和弱磁扩速能力[4]。
为实现顶驱电机与传动链之间的“柔性”连接,除电机本体外,功率变换器及其控制系统对于机组整体工作性能具有重要影响。普通电机驱动的变频调速控制在石油机械中已得到广泛应用,就HPMVM电机而言,目前的研究主要集中在电机拓扑结构和电磁分析等方面,涉及其他特性以及控制系统的研究成果相对较少。根据调磁与驱动控制的相互关系,主要分为以下2类:
1)磁通与转矩复合控制。针对交流脉冲调磁型混合永磁电机,通常采用磁场定向矢量控制技术,利用三相电枢绕组合成直轴脉冲磁动势来改变LCF的磁化水平[5]。由于电枢绕组同时具备驱动和调磁2种功能,可以通过磁通与转矩的合理配合实现协调控制,目前的研究成果有:基于定子磁链观测器的电流解耦控制可以有效抑制充/去磁过程中的转矩脉动[6],但此方法易受电机参数的影响;电流滞环PI控制避免了调磁电路频繁动作[7],但是转矩脉动较为严重;最大转矩电流比(maximum torque per ampere,MTPA)与实时磁化状态协调控制降低了系统损耗和充/去磁造成的直流母线电压波动[8],但是不同磁化状态下的MTPA曲线不同,需要测量的数据较多。
2)磁通与转矩解耦控制。针对直流脉冲调磁型混合永磁电机,在速度、电流双闭环调速系统的基础上引入在线调磁模块[9-10],该模块由DC/DC变换器和H桥功率电路组成,前者用于控制充、去磁电流幅值,后者控制磁化电流的方向和作用时间,并实现永磁双凸极与开关磁阻2种电机运行模式[11-12]。另外,还有电枢磁场重构容错控制,进一步增加电机的容错运行能力[13]。由于电枢绕组与调磁绕组在结构上完全解耦,可以根据系统控制要求实时调节LCF永磁磁化状态来确定电机的磁负荷,但是需要获取准确的实时磁链值。
基于顶部驱动钻井平台的直驱式顶驱永磁电机系统是一个庞杂的机电能量转换系统,笔者以混合永磁游标电机(hybrid permanent magnet vernier machine, HPMVM)为研究对象,在分析该电机工作原理和数学模型的基础上,设计一种抖振较小的STA滑模永磁磁链观测器,并建立不同速度区间与永磁体充/去磁状态的映射关系,实现永磁体充磁状态与速度区间的最佳优化匹配,并提出了结合分区控制的最优转矩控制策略。低速区内,饱和磁化状态时使HPMVM获得最优转矩;高速区内采用分段调磁控制,利用科恩塔克条件与电流、电压的约束构建目标函数,利用Lagrange辅助函数求取极值获得高速区内的最优转矩的输出条件。最后,通过与传统弱磁控制进行仿真对比分析,验证文中所提出控制策略的有效性。
1 HPMVM的调磁原理及数学模型
1.1 HPMVM的调磁原理
HPMVM结合了“磁齿轮”效应与“记忆电机”概念,通过磁齿轮的场调制原理,将低转速的转子磁链调制成高转速的定子气隙磁场,实现了电机大转矩的输出。HPMVM的结构如图1所示[13],该电机与传统的永磁游标电机有所不同,采用内定子结构,定子电枢齿采用深槽裂齿结构,形成24个调制极,且调磁绕组、电枢绕组和LCF永磁体均置于定子上,通过调磁绕组调节改变LCF的磁化状态,以达到改变气隙磁场的目的。转子采用外转子结构,多极对数HCF永磁体采用交替极设计,以减少永磁体使用量。
该HPMVM采用串联永磁磁路来提供气隙磁通,其调磁过程包括充磁和去磁2个过程,笔者以去磁为例分析调磁机理。电机运行之前,2种永磁体首先被正向饱和充磁。如图2所示,2种永磁体单独工作时,其工作点为P0和Q0。由于2种永磁体是串联的机制,所以具有相同的磁密,工作点也互相影响,实际的工作点将会发生偏移,即从P0、Q0转移到P2、Q2。当施加一定的负向去磁电流脉冲时,HCF永磁体的工作点将沿着Q2Q1移动,最终稳定工作点Q1,LCF永磁体的工作点将沿着P2P0P-P3P1移动,最终稳定在P1点。若施加更强的退磁电流脉冲,其永磁体工作点的运动情况与前面叙述相似。
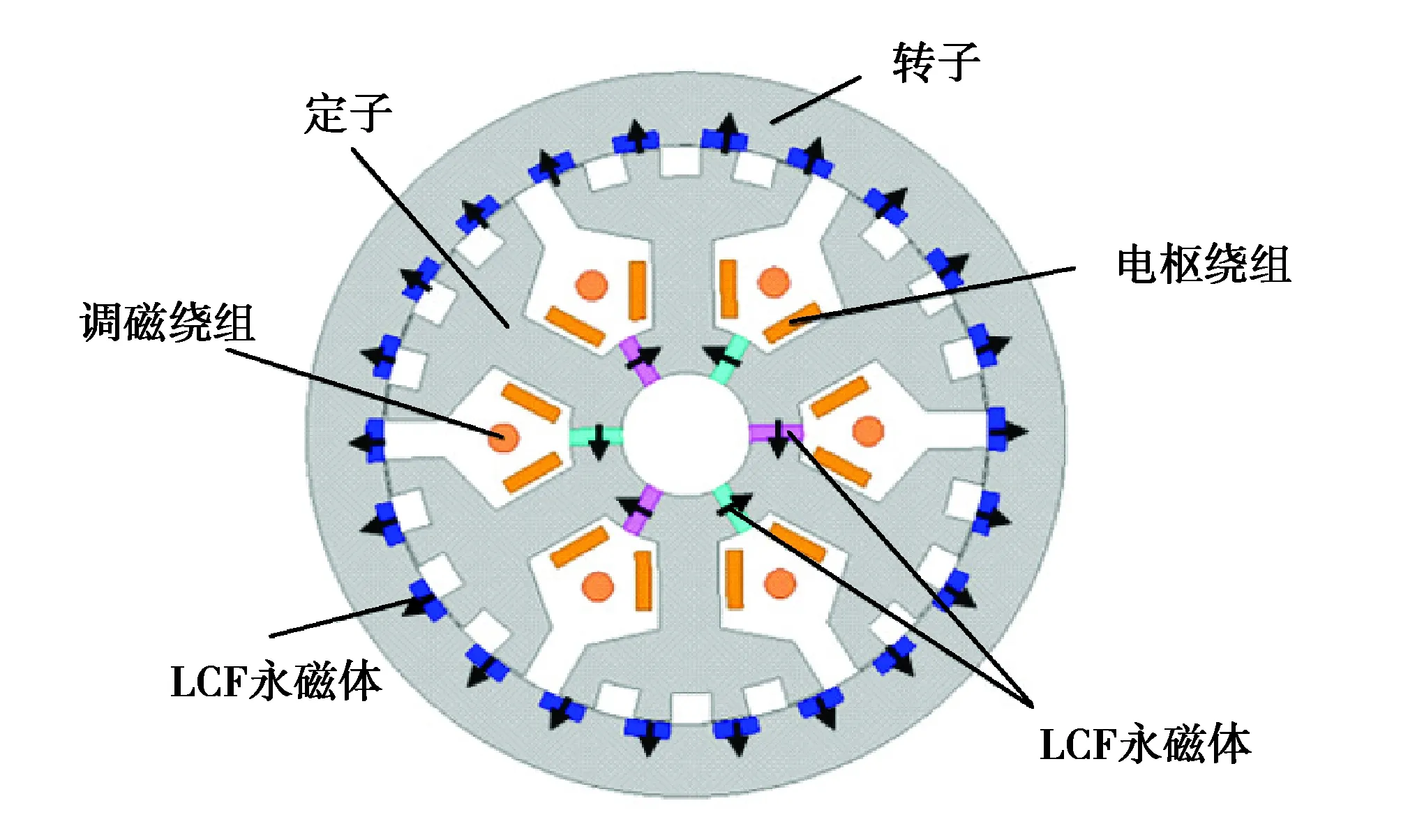
图1 混合永磁游标电机Fig. 1 Hybrid permanent magnet vernier machine
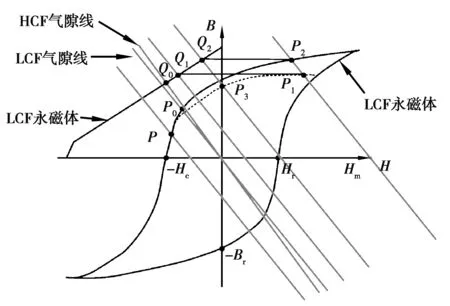
图2 HPMVM调磁机理图Fig. 2 Magnetic modulation mechanism diagram of HPMVM
1.2 HPMVM的数学模型
忽略温度和涡流损耗等因素的影响,根据电机工作原理,构建如图3所示的HPMVM的等效物理模型。根据图3中的HPMVM等效模型,可以得到HPMVM在两相旋转dq坐标下的数学模型。
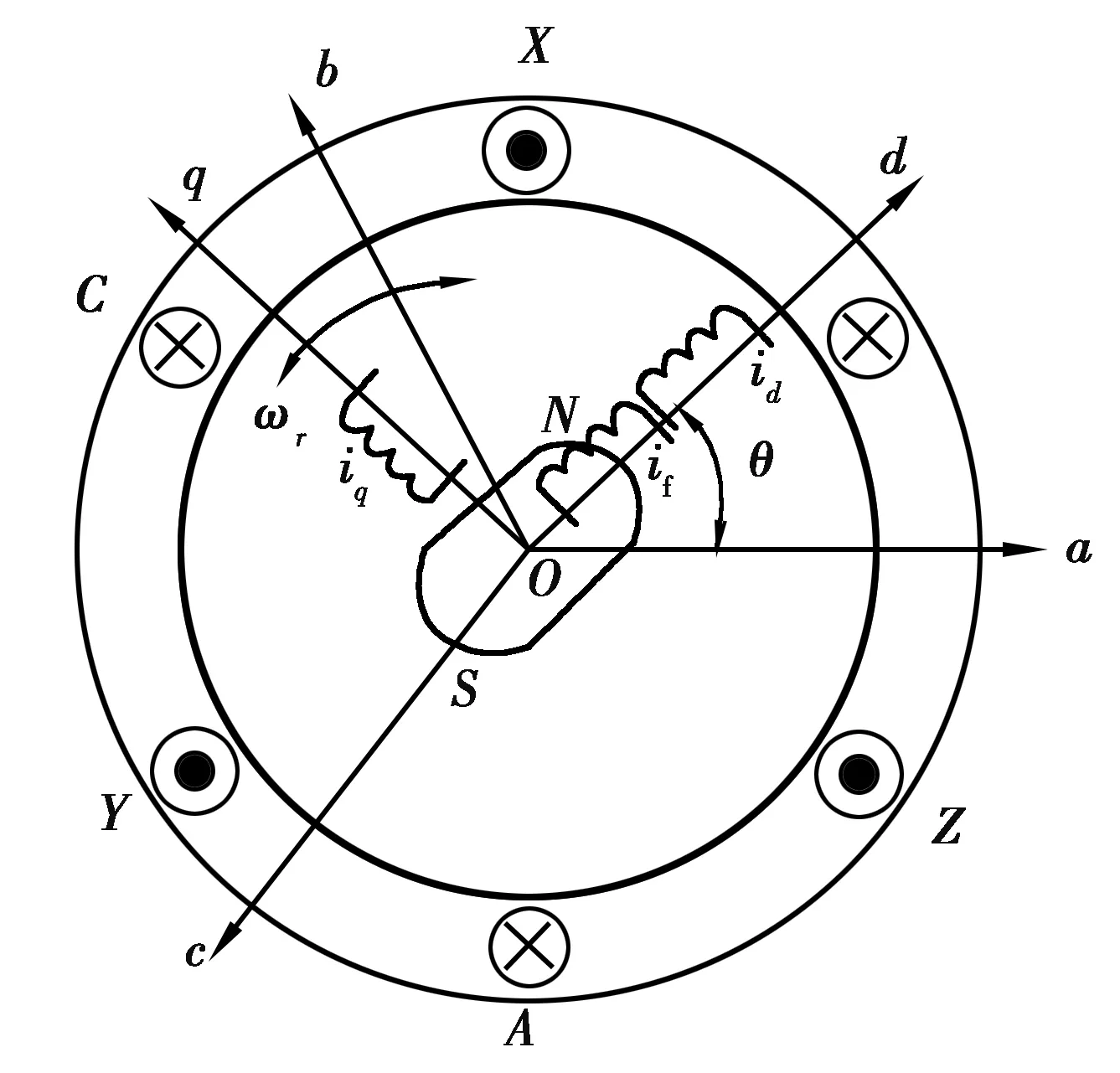
图3 dq坐标系下的HPMVM的物理模型Fig. 3 Physical model of HPMVM in dq coordinate system
定子绕组的磁链方程为:
(1)
式中:Ld和id分别为电机定子绕组d轴电感和电流;Lq和iq分别为电机定子绕组q轴电感和电流;ψd、ψq为电机的d轴和q轴的磁链;ψf、ψpm(if)和ψfpm(if)分别为了励磁绕组磁链、永磁磁链和砸链到励磁绕组永磁磁链;Msf为励磁绕组和电枢绕组之间的互感;if为调磁脉冲电流。
电压方程为
(2)
式中:R1为电机定子相绕组的电阻;ud和uq分别为电机定子绕组d轴电压和q轴电压;ω为电机转子旋转电角速度。
转矩方程为
(3)
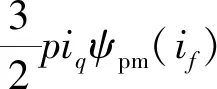
2 基于STA的永磁磁链观测器设计
在HPMVM调磁过程中,施加调磁脉冲的幅值取决于电机当前磁化状态和目标磁化状态。要实现恰当的充/去磁控制,需要解决以下问题:
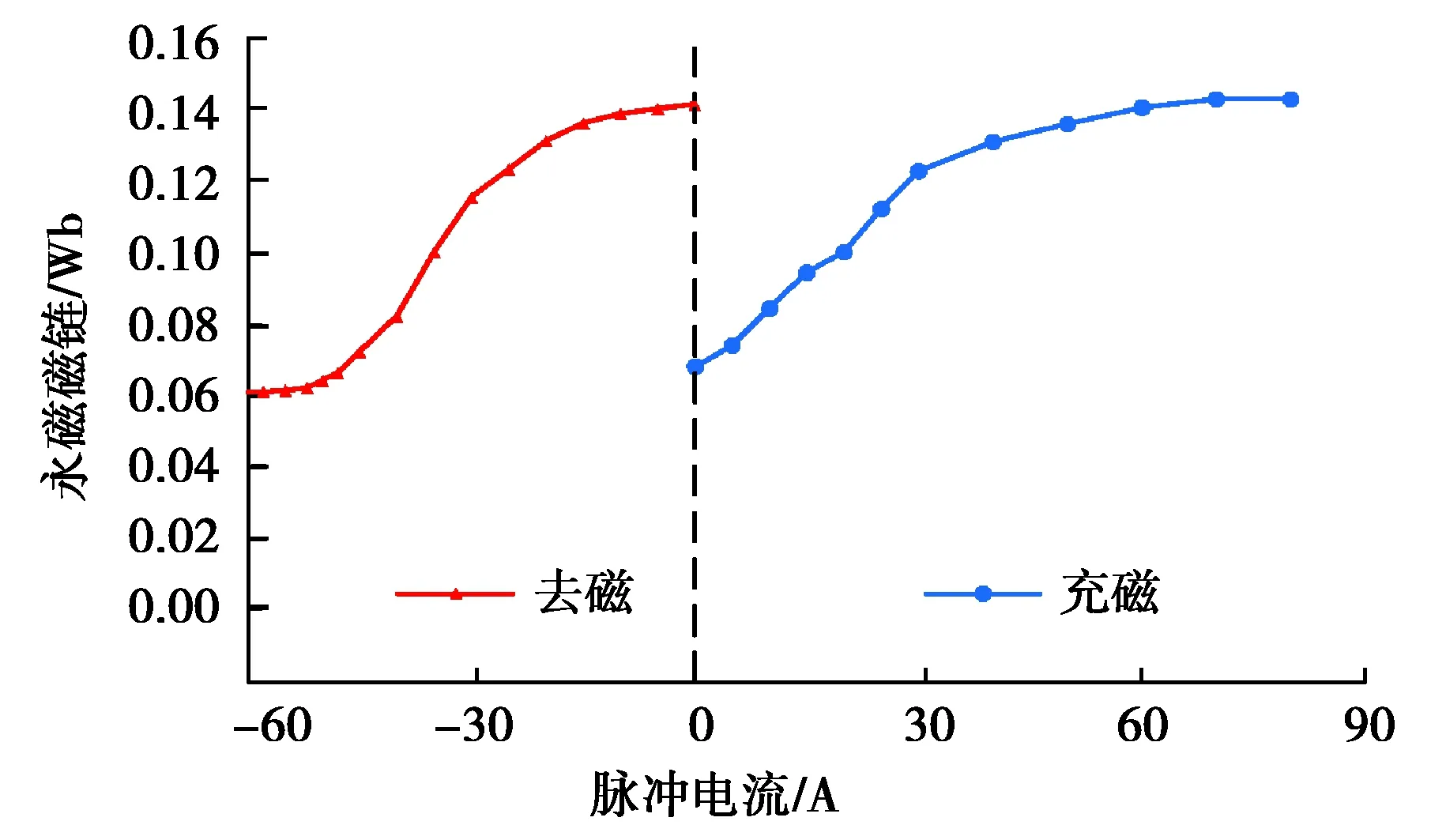
图4 永磁磁链与调磁脉冲关系Fig. 4 Relationship between permanent magnet flux linkage and modulation pulse
1)明确永磁磁链与调磁脉冲之间的变化关系。通过有限元分析获得如图4所示调磁脉冲与永磁磁链之间的对应关系。HPMVM正向充磁与反向去磁均具有饱和非线性,由于2种永磁体之间采用串联调磁机理,高矫顽力永磁体对低矫顽力充/去磁的影响较大,导致HPMVM磁链调节特性曲线并不对称。
2)获得电机的实时永磁磁链。目前检测的主要方法有:文献[14]采用自适应观测法,实现了电机的多个参数的同时辨识,但是各个参数的之间的交叉耦合易造成系统不稳定;卡尔曼滤波磁链观测法[15],此方法观测精度较高,然而计算较为复杂;滑模观测法[16]存在系统抖振的问题。文中设计了一种抖振较小的STA滑模永磁磁链观测器,下面进行具体说明。
2.1 超螺旋算法
文献[17]中利用Lyapunov理论证明了STA的连续性与稳定性。STA滑模控制由扰动项ρ1(x1,t)、ρ2(x2,t)和不连续滑模变量sgn函数两大部分组成,为
(4)
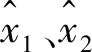
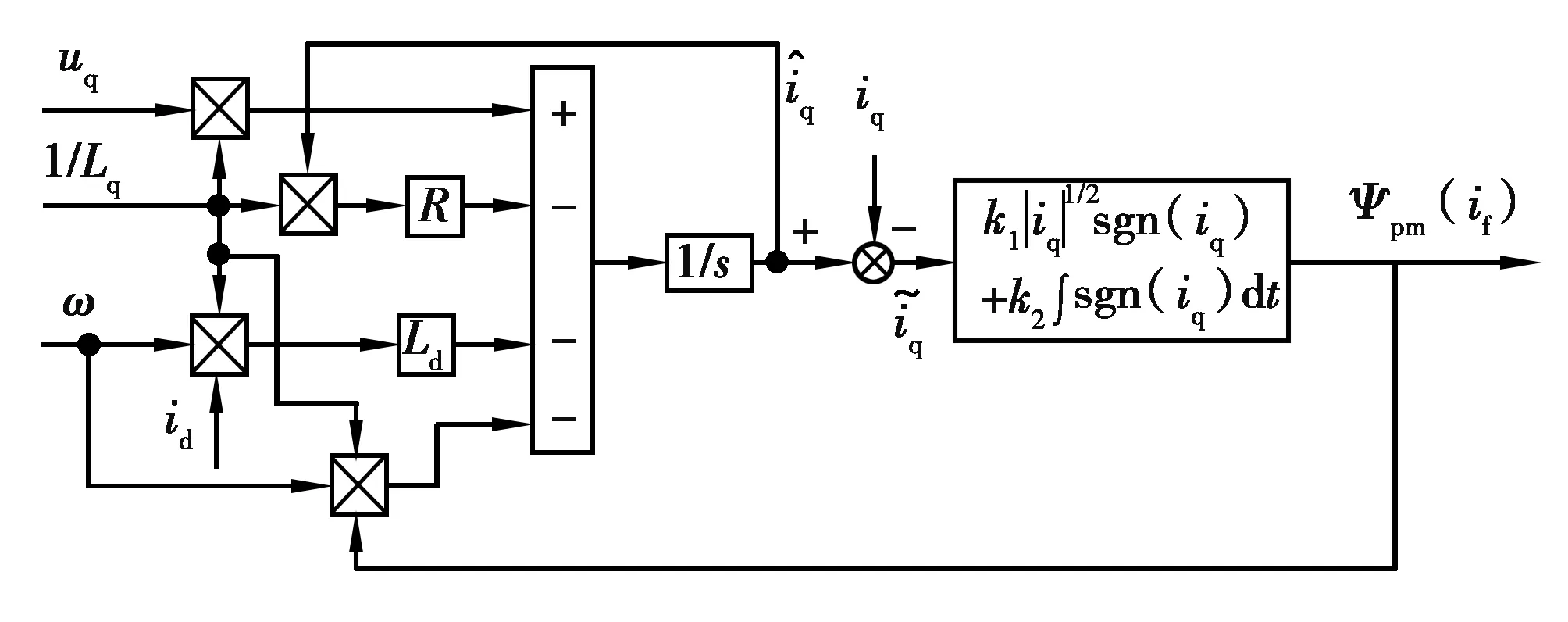
为了保证系统在一定时间内收敛到滑模面,则扰动项必须全局有界,即ρ1(x1,t)≤σ|x1|r(σ为任意正常数),0 (5) 忽略调磁脉冲动态变化的影响,结合式(1)和式(2),可得: (6) 由式(6)可知,永磁磁链只出现在q轴的方程中,因此将q轴方程写成 (7) 式中,eq为永磁磁链旋转电动势在q轴上的分量。A=-R/Lq,B=1/Lq,u=uq-Ldωid,Ke=-1/Lq,eq=ωψpm(if)。 根据式(4),设计如下二阶滑模观测器: (8) (9) 当σ≫0时,满足下列不等式 (10) 满足式(9)和式(10),则保证了在有限的时间内,系统能够收敛到滑模的超平面。式(8)减去(7)得 (11) (12) 经以上分析,构建如图5所示的STA滑模永磁磁链观测框图。 图5 STA滑模永磁磁链链观测框图Fig. 5 Observation block diagram of STA sliding mode permanent magnet flux linkage 考虑到电机的发热以及逆变器容量等因素,电机在运行时定子电压、电流和调磁绕组电流必须限制在允许的范围内。基本的约束关系为 (13) 式中:ismax、usmax分别为电机定子电流和电压的极限值;ifImax、-ifDmax分别为充去磁过程中极限脉冲电流值。 在同步旋转坐标系中,采用id=0控制,忽略定子电阻压降,电机稳态时电压限制椭圆方程的数学表达式为 (14) 式中,Udc为逆变器直流侧电压。 图6为HPMVM定子电流和电压极限约束示意图。在相同的磁化状态下,定子电压椭圆的中心位置不变,但是随着电机转速的升高逐渐向内收缩;磁化状态发生变化时,其定子电压极限椭圆的中心位置将在直轴上移动,运动区间为[xa,xb]。 图6 HPMVM定子电压和电流的极限约束Fig. 6 Limit constraints of stator voltage and current for HPMVM 在直流母线电压恒定的条件下,随着电机转速逐渐升高,反电势的幅值逐渐达到电压极限时,若不采用弱磁控制,则电机转速无法继续升高。利用HPMVM磁化状态可调特性,进一步拓宽电机的调速范围。然而,若连续调节电机磁化状态,则会使励磁损耗增加,甚至导致逆变器功率器件发生不可逆损害。为了避免此问题,文中采用了分区控制。如图7所示,在整个运行过程中,将电机运行区域划分为低速区和高速区,在低速区保持饱和磁化状态运行,电机获得最大转矩输出能力;高速区结合分段调磁实现最优转矩控制。 图7 HPMVM分区控制图Fig. 7 HPMVM partition control chart 考虑定子极限电压约束,由式(14)变形得到电机在稳态时永磁磁链与转速的关系: (17) 文献[18]中,定义目标函数为 f=-(ψpm(if)+Mfif)iq, (18) 式中,永磁磁链和交轴电流均为变量,并满足电流和电压的约束条件。 (19) 式中,iN为额定相电流。 构建Lagrange辅助函数: F=f+λ1h1+λ1h1, (20) 式中,λ1和λ2分别为拉格朗日乘子。 分别对式(20)中ψpm(if)、iq、λ1和λ2求偏导,得到: (21) 忽略脉冲电流,由式(21)得到最优转矩的输出解为 (22) 式(22)表明,交轴电流位于定子电流极限圆的边界上时获得最优输出转矩,如图8所示。ψpm(if1)、ψpm(ifk)分别为永磁磁链的边界值,与额定电流的交点分别为A点和B点,则区间AB为HPMVM获得最优转矩控制点的变化范围。 图9为转速与磁链之间的关系图,n0、n1…nk为不同转折速度,对应转折磁链为ψpm(if1)、ψpm(if2)…ψpm(ifk),其中n0=nN(nN为额定速度)。若永磁磁链观测值ψpm(if)<ψpm(ifi)(i=1,2…k),则施加正向调磁脉冲,若永磁磁链观测值ψpm(if)>ψpm(ifi)(i=1,2…k),需施加反向调磁脉冲。否则,无需施加调磁脉冲。 图8 最优转矩输出工作点的运行轨迹Fig. 8 Running track of optimal torque output operating point 图9 电压(磁链)速度曲线Fig. 9 Voltage (flux linkage)-speed curve 为了验证文中所提出控制策略的有效性,在Simulink中搭建了HPMVM驱动控制系统的仿真模型,控制框图如图10所示,部分仿真参数如下:额定转速136 r/min,转子极对数22,绕组极对数2,定子齿数24,直流母线电压510 V,转动惯量0.000 8 kg·m2,摩擦系数0.000 1,定子绕组电阻1.09 Ω,直轴电感8.77 mH, 交轴电感12.87 mH,永磁磁链0.06~0.14 Wb。 图10 HPMVM电机控制系统框图Fig.10 Block diagram of HPMVM motor control system 额定转速以下属于低速区,转矩设定为20 N·m;额定转速以上的属于高速区,将高速区间划分为区间一[136,180]和区间二[180,300],并以180 r/min和250 r/min为速度转折点,对应转矩给定分别为15 N·m和11 N·m。 图11为HPMVM连续去磁的运行特性曲线。采用id=0控制,整个过程中,初始转速给定为136 r/min,2 s时突变为180 r/min,3 s时突变为250 r/min。 永磁磁链分析:图11(a)和图12(a)为永磁磁链的观测图,由图可知STA滑模观测器在稳定性、快速性及抖振上均优于普通的指数滑模观测器。在图11(a)(b)中,2 s以前电机以饱和磁化状态运行,磁链的观测值为0.14 Wb;2 s时施加幅值为-26 A的去磁电流脉冲,永磁磁链的幅值降为速度区间[136,180]对应的磁链幅值0.11 Wb;3 s时施加了-58 A的去磁电流脉冲,永磁磁链的幅值也降为速度区间[180,300]所对应的磁链幅值0.06 Wb。 图11 HPMVM去磁运行特性Fig. 11 Operating characteristics of HPMVM demagnetization 转速分析:由图11(c)可知,2 s以前电机以额定转速136 r/min运行,2 s以后减小电机永磁磁链的幅值进入了高速区间。由图11(a)和(c)可知,通过调节永磁磁链,电机的转速由136 r/min提升到250 r/min,且转速能较快地跟随给定值。然而与传统的弱磁控制相比,永磁磁链幅值的降低使得电机的响应速度变慢。 转矩及损耗分析:由图11(d)可知,电磁转矩能较快地跟随给定值,但最优转矩由于磁链的减小,转矩响应慢于传统的弱磁控制;由11(e)~(g)可知,最优转矩控制下的直轴电流基本无静差跟踪参考值,交轴基本保持在8 A左右,与弱磁控制相比,最优转矩控制的铜耗较小。同时,转矩恒定时,较高的永磁磁链能够降低电机定子的电流,以此减小损耗,进而提升系统的效率。 图12为HPMVM充磁运行特性仿真分析。此过程中,初始电机转速为200 r/min,2 s后给定为160 r/min,3 s后给定为120 r/min。 永磁磁链及转速分析:在图12(a)~(c)中,电机初始磁链给定为0.06 Wb,2 s、3 s时分别施加了幅值为32 A和70 A的充磁脉冲电流,永磁磁链的幅值也上升到0.09 Wb和0.13 Wb,转速也由最初的200 r/min下降到150 r/min和120 r/min。 转矩分析:由图12(b)~(e)可知,电机的初始电磁转矩为10 N·m,在2 s、3 s时分别施加了不同的充磁电流脉冲后,转矩相应由最初的10 N·m提升到15 N·m和20 N·m;其直轴电流保持为0,交轴电流脉动较大,造成了转矩脉动较为严重,这将需要进一步研究解决。 图12 HPMVM充磁运行特性Fig.12 Operating characteristics of HPMVM magnetization 采用分段调磁控制的HPMVM转矩与速度曲线如图13所示。由图13可知,通过调节电机的永磁磁链,电机的转折速度由136 r/min提升到250 r/min,表明了此方法显著拓宽了HPMVM的调速范围。 图13 HPMVM转矩速度曲线Fig. 13 Torque-speed curve of HPMVM 以直驱式顶驱驱动系统为研究背景,以HPMVM作为驱动装置。在分析了HPMVM调磁原理和数学模型的基础上,设计了STA滑模永磁磁链观测器,并结合HPMVM磁链可调特性在全速域内提出了基于分区控制的最优转矩控制策略,主要得到以下的结论: 1)STA滑模磁链观测器能够快速识别HPMVM转子磁链,且精度较高,抖振较小。 2)与传统的弱磁控制相比,最优转矩控制实现了全速域内最大转矩的输出,并降低了电机的铜耗,然而永磁磁链的降低也导致了电机响应速度变慢。 3)在恒负载的情况下,较大的永磁磁链能够降低电机的定子电流,进而提升整个系统的效率。2.2 永磁磁链观测器的设计
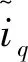
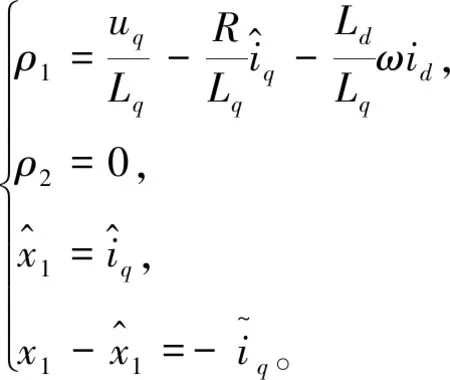
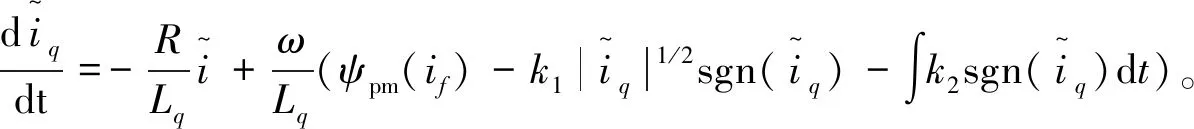
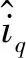
3 HPMVM控制策略
3.1 电压和电流极限约束
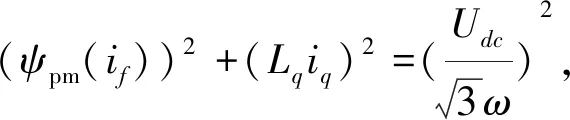
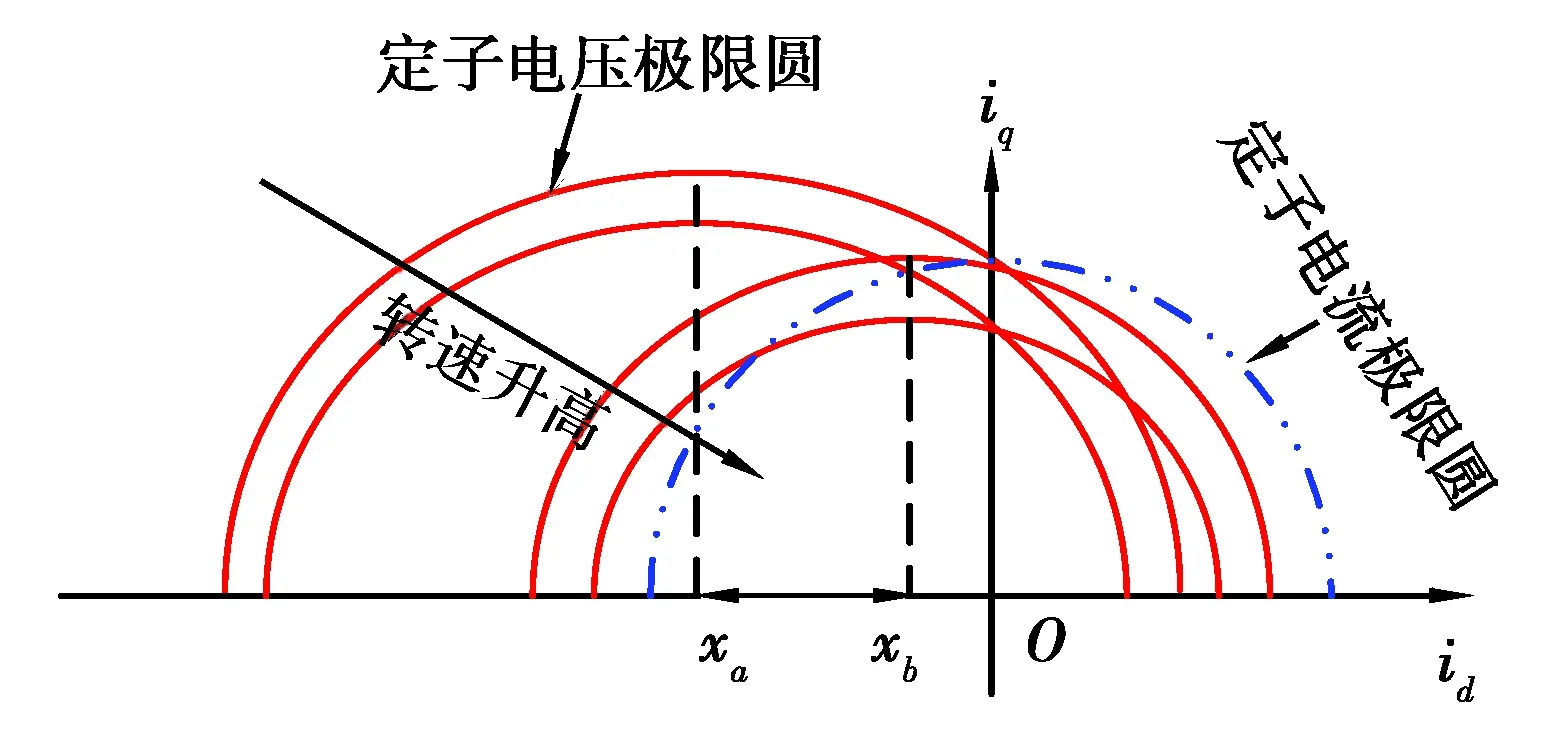
3.2 最优转矩控制
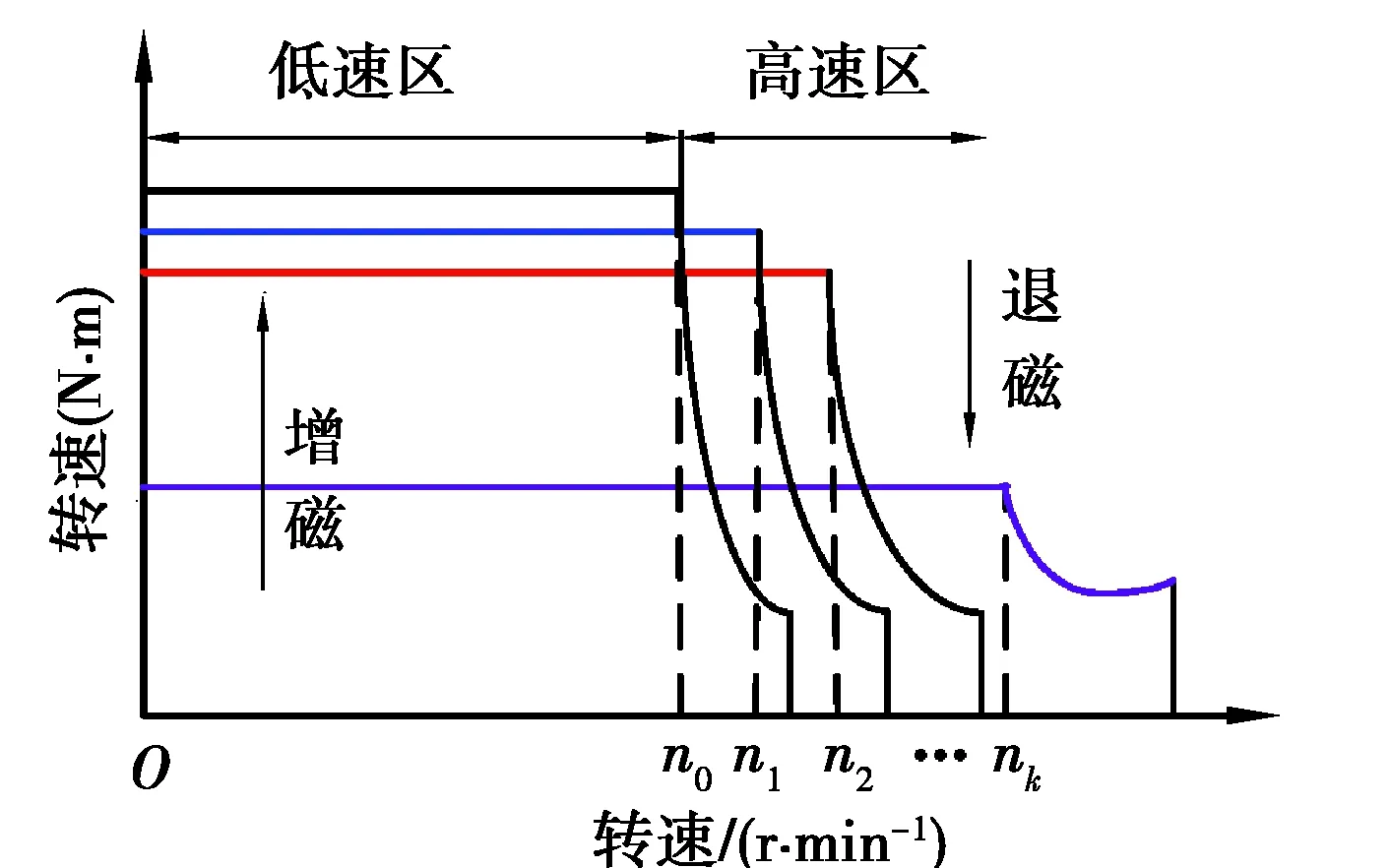
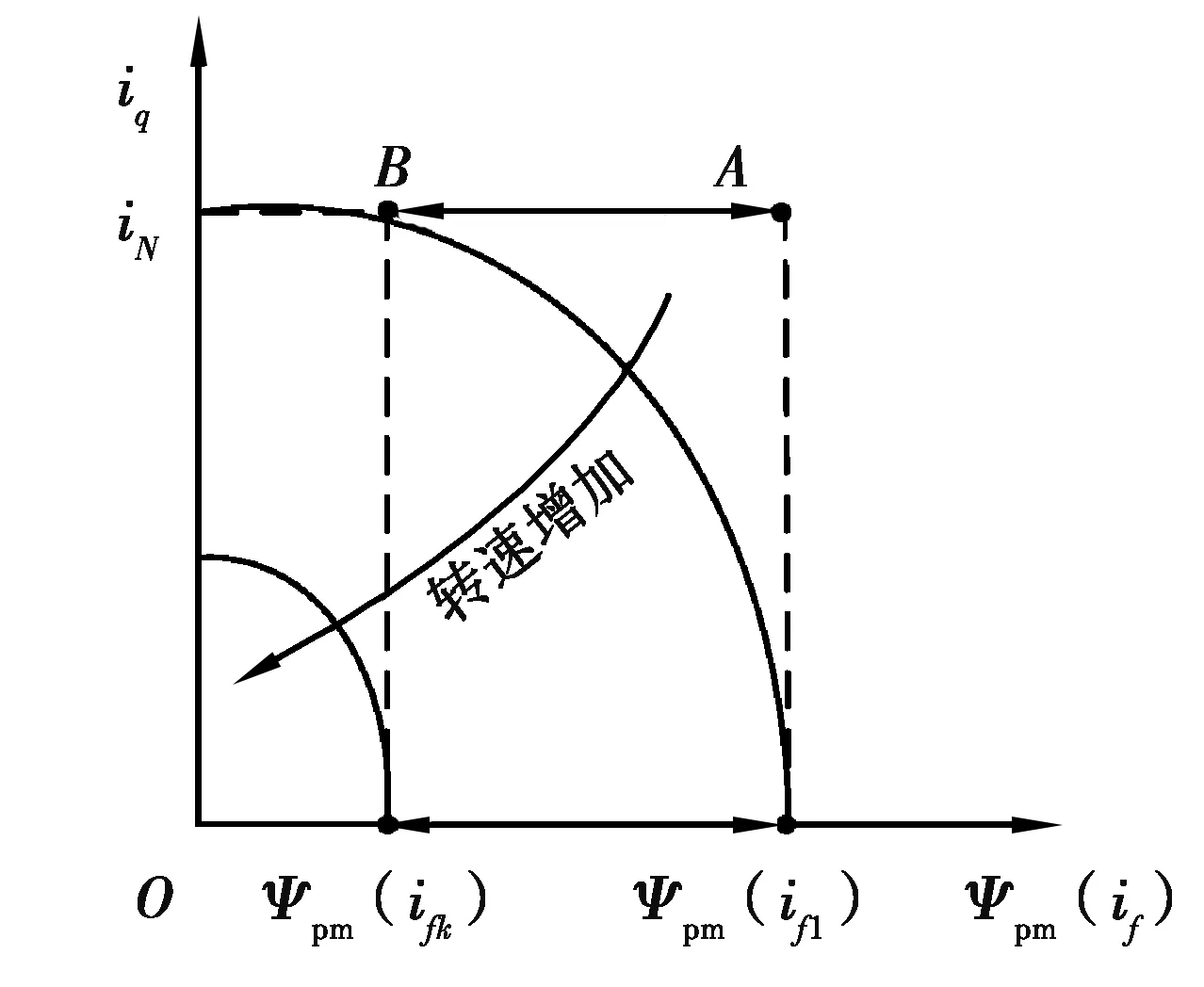

4 仿真分析
4.1 系统组成

4.2 去磁运行分析
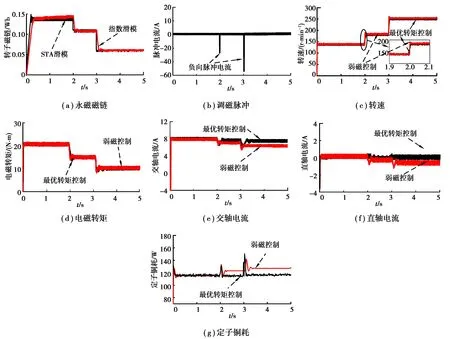
4.3 充磁运行分析
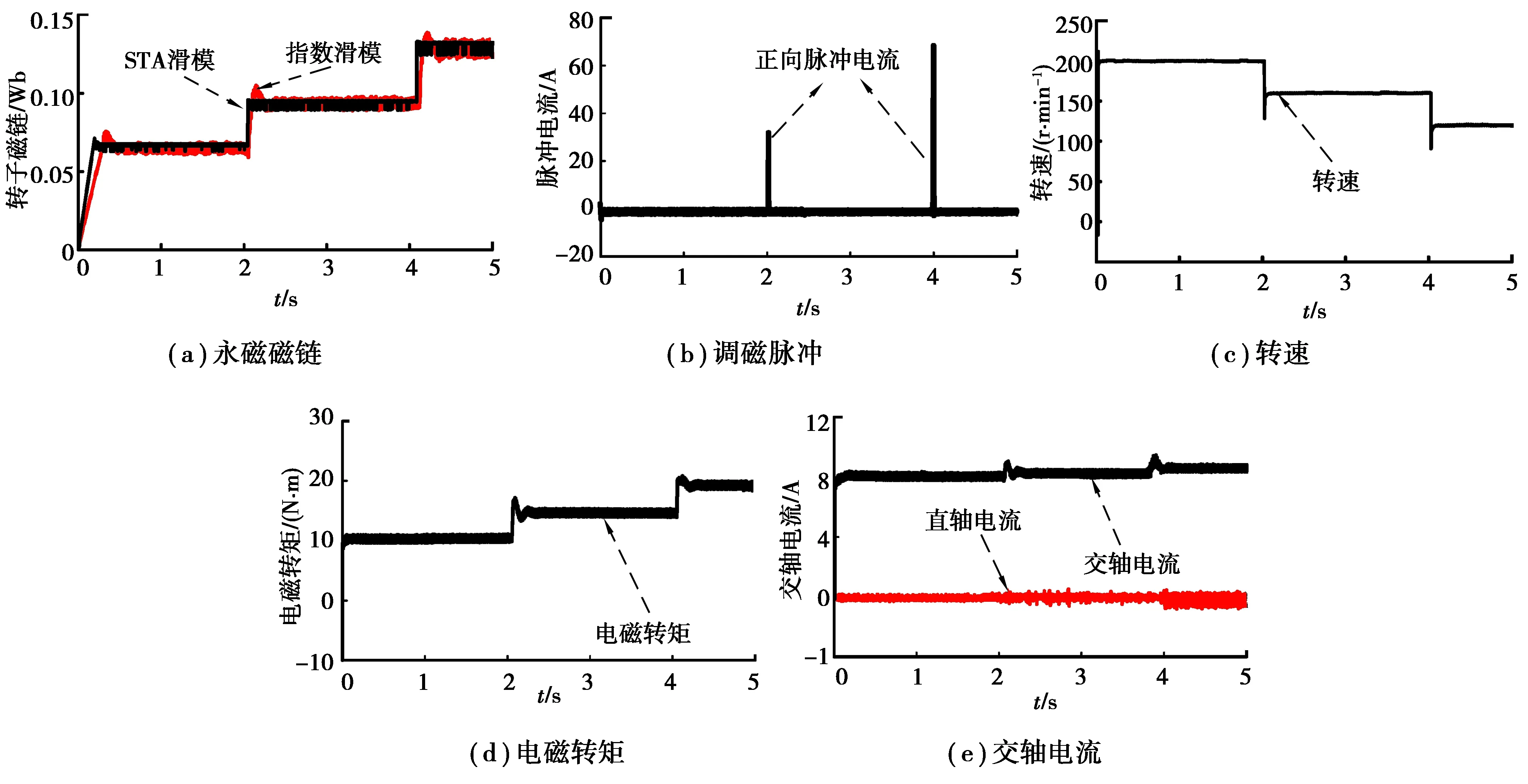
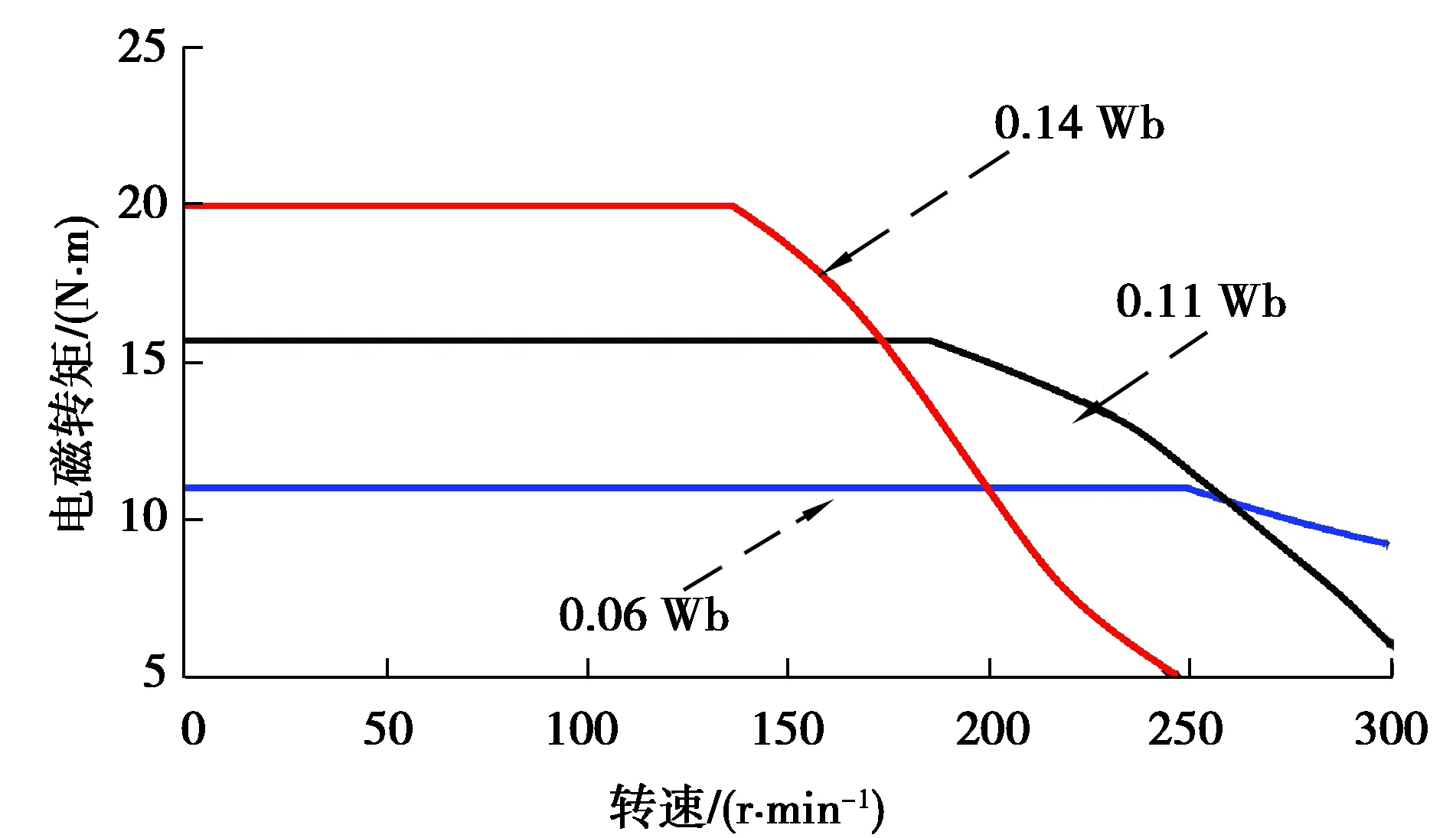
5 结 论

