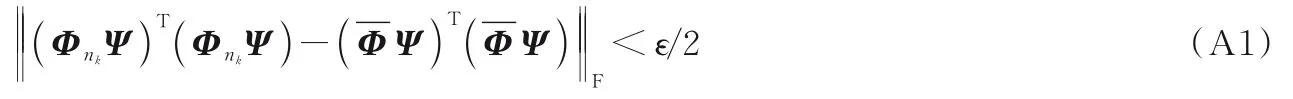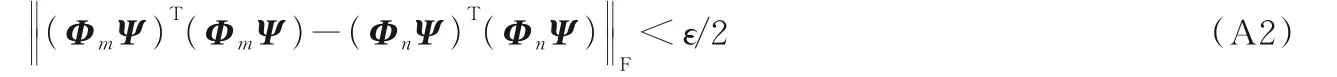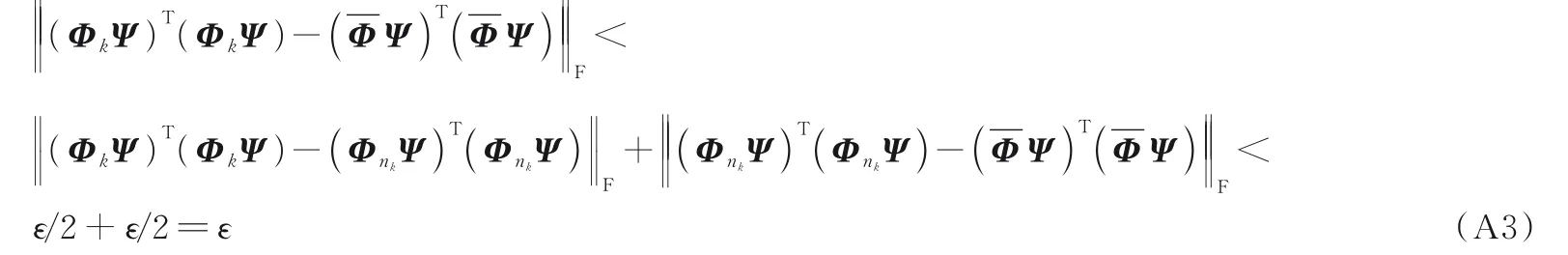压缩感知中提升测量矩阵稀疏性的等效字典优化设计
陈映瞳
(西安工业大学基础学院,西安 710021)
引 言
压缩感知是一种新型信号观测与恢复方法,在机械故障诊断[1]、材料的冲击损伤检测[2]等领域得到了广泛应用。这种方法的主体是由测量矩阵、稀疏字典和稀疏重构算法组成的压缩感知系统,其中稀疏重构算法的稳定性是衡量压缩感知系统重构性能的重要指标。因此,如何提升稀疏重构算法的稳定性是压缩感知方法的一个重要研究课题。研究表明等效字典的互相干性值越小(即它的互不相干性越强),稀疏重构算法的稳定性就越强。因此,提升压缩感知系统重构性能的一条重要途径就是减小等效字典的互相干性值。这方面的研究工作最早开始于2007年[3⁃4],近年来关于此的研究成果仍不断涌现。文献[5]把测量矩阵和稀疏字典放在一起进行优化设计,使得等效字典具有更小的互相干性值,稀疏重构算法则具有更强的稳定性,最终使得压缩感知系统具有更高的信号重构率。文献[6]在交替投影算法框架下提出了一种优化设计方法。在每步迭代中,首先固定稀疏字典,通过令等效字典的Gram矩阵逼近某类特定Gram矩阵来优化设计测量矩阵,然后固定测量矩阵,利用一组训练数据,通过极小化稀疏表示误差在测量前后的能量和,优化设计稀疏字典。该方法每步迭代的两个子步骤分别采用不同的目标函数,为了简化设计过程,文献[7]采用统一的目标函数优化设计测量矩阵和稀疏字典。为了改进文献[6]方法不能处理海量训练数据的不足,基于固定稀疏字典优化设计测量矩阵的方法[8],通过借鉴文献[9]中的在线字典学习方法,文献[10]提出了一种高效的等效字典优化设计方法。文献[11]采用交替投影方法极小化等效字典的Gram矩阵与某类特定Gram矩阵的差,其间采用共轭梯度法更新等效字典。尽管这些方法设计的等效字典在图像恢复任务上都取得了较好的数值实验效果,但在进行优化设计时都没有考虑到等效字典对后续信号重构效率的影响。
还有一些工作简化了联合优化设计方式,即在稀疏字典固定的情形下,仅对测量矩阵进行优化设计。文献[12]采用交替投影方法极小化等效字典的Gram矩阵与某类特定Gram矩阵的差,但在设计等效字典时没有考虑它对信号重构效率的影响。文献[8]在极小化等效字典的Gram矩阵与某类特定Gram矩阵的差时,通过对目标函数添加正则项,使得能够利用设计好的等效字典较好地重构了不是严格稀疏的信号。文献[8]在进行优化设计时,没有考虑如何才能利用设计结果更有效地重构信号。为此,文献[13]对文献[8]中优化问题的变量(即测量矩阵)赋予了稀疏结构,要求等效字典是按行稀疏的测量矩阵(每行的稀疏度是固定的)和某个正交矩阵(例如离散余弦变换矩阵)的乘积。这种方法能有效提升测量矩阵的稀疏性,但提出的结构有可能阻碍了测量矩阵稀疏性的进一步提升。同时,这种方法对每步迭代中的梯度下降采用回溯准则选取步长,导致方法的时间复杂度较高。和文献[8]类似,为了能够利用优化设计的等效字典较好地重构不是严格稀疏的信号,文献[14]在极小化等效字典的Gram矩阵与某类特定Gram矩阵的差时,对目标函数添加了一个包含训练数据稀疏表示误差的正则项,但在进行优化设计时都没有顾及等效字典对信号重构效率的影响。文献[15]利用光滑化技巧把极小化等效字典互相干性值的问题转化为一个有约束光滑优化问题,然后利用交替投影方法进行求解。这种方法能显著减小等效字典的互相干性值,但和文献[8]一样,在提高信号重构效率上还有进一步提升空间。
从上述方法分析可知:当前的等效字典优化设计方法普遍没有考虑等效字典对后续信号重构效率的影响。为此,本文准备固定稀疏字典,极小化等效字典的Gram矩阵与某类特定Gram矩阵的差,同时要求测量矩阵满足某种基于L1范数的不等式约束。利用L1范数的促稀疏性,可在算法进行过程中自动让测量矩阵中的部分元素归零,从而提高后续利用等效字典进行信号重构的效率。然后,基于交替投影方法求解提出的最优化问题,并保证算法的收敛性。和相关方法相比,本文提出的优化设计方法着重关注测量矩阵的稀疏性对后续信号重构效率的影响。利用这种方法优化设计等效字典,有望在信号重构阶段获得更高的重构精度和重构效率。
1 本文优化设计方法
1.1 极小化问题
压缩感知的测量模型是y=Φx+e,其中y∈RM为测量值,Φ∈RM×N(M≪N)为测量矩阵,e为测量噪声,x∈RN为待重构信号,在稀疏字典Ψ∈RN×L(N≤L)下有稀疏表示x=Ψα+n,其中α为稀疏向量,稀疏度(向量的零范数即指它的非零分量个数),n为稀疏表示误差。则乘积A=ΦΨ被称为等效字典。
在稀疏字典Ψ固定的情形下,本文通过求解极小化问题(1)优化设计测量矩阵。

问题(1)的解之所以能更稳定地重构稀疏信号且问题(1)的解有一定稀疏性有以下原因。首先,周知L1范数具有促稀疏性,所以通过约束条件可以迫使测量矩阵的部分元素归零。而且和文献[13]稀疏化测量矩阵的方式相比,这种方式没有硬性规定测量矩阵每一行的稀疏度,所以有可能使得测量矩阵具有更强的稀疏性。其次,集合X描述的是一类理想等效字典的Gram矩阵。这类等效字典的每列具有单位L2范数,且它的互相干性值不超过ξ,ξ为M×L维矩阵所能达到的最小互相干性值。根据压缩感知中常用稀疏重构算法(例如正交匹配追踪算法(Orthogonal matching pursuit,OMP)和基追踪去噪算法(Basis pursuit denoising,BPDN)等)的稳定性保证[16]可知,相较其他M×L维等效字典,这类等效字典搭配常用稀疏重构算法构成的压缩感知系统,能在最坏意义下具有一定稳定性。因此,通过让等效字典的Gram矩阵尽可能接近集合X,可使等效字典在后续重构阶段带来更高重构精度。
1.2 求解算法及其收敛性
本节给出极小化问题(1)的解法。将极小化问题(1)改写成如式(2)所示的等价形式。
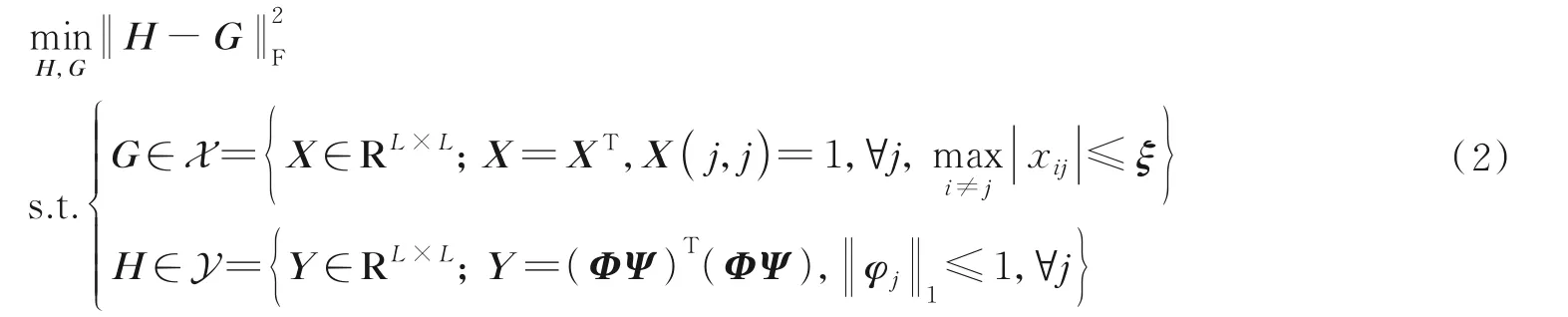
本文根据交替投影算法框架求解最优化问题(2)。固定稀疏字典Ψ,设在交替投影算法第k步迭代开始时测量矩阵是Φk,在第k步迭代中交替进行如下两个步骤。
(1)求Gram矩阵G=(ΦkΨ)T(ΦkΨ)在集合X上的投影,即对G按元素执行如下操作
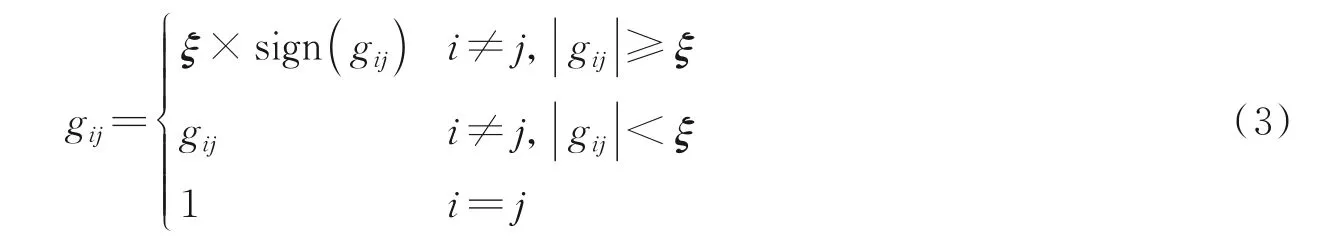
式中sign(⋅)是符号函数(规定sign(0)=0)。将投影记为G k。
(2)固定G k求解优化问题(2),即求G k在集合Y上的投影。这时,优化问题(2)可以等价写为
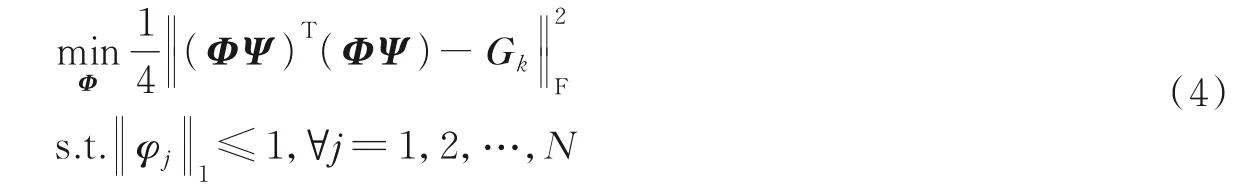
采用梯度投影算法[17]求解问题(4)。把目标函数记为f(Φ)。按文献[18]中的算法求Φk在集合Z上的投影,集合为了简便,投影仍记为Φk,把Φk作为问题(4)的初值。然后选定常数s>0,执行若干步如下操作:按文献[18]中的算法求在集合Z上的投影͂。其中,梯度然后,从Φ开始沿方向前进步长α∈(0,1),α按Armijo准则选取。设参数β、σ∈(0,1),找到使得式(5)成立的最小非负整数m,然后得到步长α=βm。

执行完若干步迭代后,把新的测量矩阵记为Φk+1。这样就完成了交替投影算法的第k步迭代。如此进行若干步交替投影后,输出最终的测量矩阵Φ。
综上,本文提出的等效字典优化设计方法的步骤如下。
输入:测量矩阵Φ∈RM×N,稀疏字典Ψ∈RN×L,交替投影算法的迭代步数Talter,梯度投影算法的迭代步数T,参数s>0和β、σ∈(0,1),Φ的行数M;Ψ的列数L。
fork=1:Talter
计算A=ΦΨ和G=ATA;对G按元素执行式(3)操作;
按文献[18]中的算法求Φ在集合Z上的投影,投影仍记为Φ;
fort=1:T
计算B=Φ-s∇f(Φ);
按文献[18]中的算法求B在集合Z上的投影,投影记为;
利用Φ,Φ͂,Ψ,G,β和σ,按Armijo准则选取步长α;
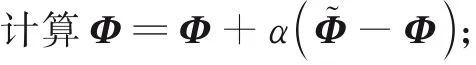
end
end
输出:测量矩阵Φ。
本文提出的优化设计方法通过计算B的每列在L1范数单位球上的投影,求B在集合Z上的投影。在求B中任意一列在L1范数单位球上的投影时,本文具体采用的是文献[18]中的算法。
下面从两个方面说明本文提出的等效字典优化设计方法是收敛的。首先,单看每步交替投影用到的梯度投影算法。因为集合Z是有界集,所以梯度投影算法求解问题(4)产生的序列至少会有1个聚点。根据文献[17]可知,这个聚点是优化问题(4)的稳定点。其次,来看整个交替投影算法。根据文献[19]可知,因为集合X和Y都是有界闭集(关于Y的闭性,详见附录),所以本文提出的交替投影算法是收敛的。具体来说,设X k∈X是第k步交替投影产生的Gram矩阵,是第k步交替投影产生的测量矩阵对应的Gram矩阵,则序列至 少 会 有 一 个 聚 点且 有:(1),即̂是̂在集合Y上的投影;(3),即̂是在集合X上的投影。
为了便于理解,对上述收敛性结果进行简要解释。“集合Y是RL×L的子集”可以一般化为“G是任一距离空间S的任意非空子集”,“集合X是RL×L的子集”可以一般化为“H是任一距离空间T的任意非空子 集”。问 题(2)的 目 标 函 数 是RL×L×RL×L上 的 连 续 实 值 函 数∀(Y k,X k)∈G×H,k=2,3,…,“用梯度投影法求解问题(4)进而得Y k+1”可以抽象成一个从G×H到G×H的集值映射F1(Y,X)=M G(X)×{X},其中M G(X)表示给定X∈H后f(Y,X)在G上的全局极小点集,具体就是Y k+1∈M G(X k),(Y k+1,X k)∈F1(Y k,X k)。∀(Y k+1,X k)∈G×H,k=2,3,…,执行式(3)操作得到X k+1也可以抽象成一个从G×H到G×H的集值映射F2(Y,X)={Y}×M H(Y),其中M H(Y)表示给定Y后f(Y,X)在H上的全局极小点集,具体就是{X k+1}=M H(Y k+1)(这里用等号,因为式(3)操作的结果是单点集),(Y k+1,X k+1)∈F2(Y k+1,X k)。因此,对所提交替投影算法,如果设X k∈H是第k步交替投影产生的Gram矩阵是第k步交替投影产生的测量矩阵Φk+1对应的Gram矩阵,则序列{(Y k,X k)}∞k=1满足(Y k+1,X k+1)∈F(Y k,X k),k=2,3,…,其中是F1和F2的复合,它的对应法则为
有了上述转化后,就能应用如下定理1得到所提交替投影法的收敛性结果,即序列至少有一个聚点且有同时还有Ŷ是X̂在集合Y上的投影,X̂是Ŷ在集合X上的投影。另外,定理1可由文献[20]中的收敛性结果得出。
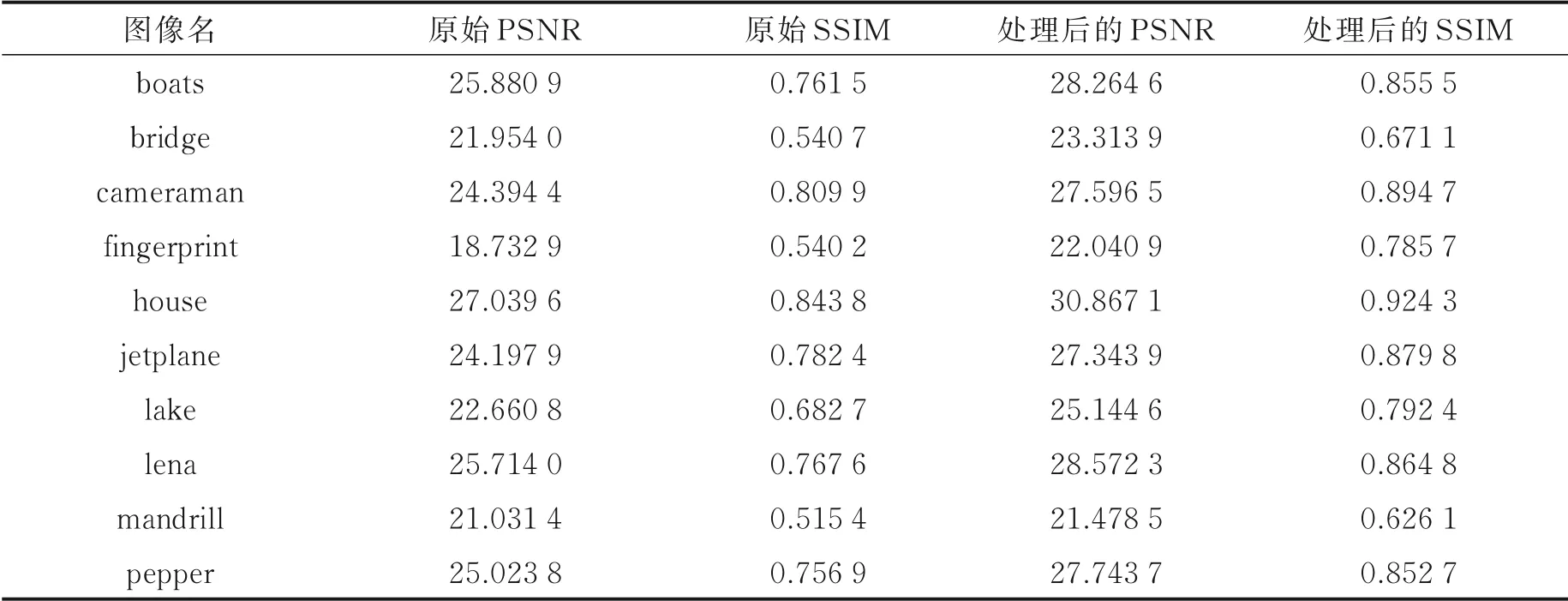
定理1设S,T都是距离空间,G⊂S和H⊂T都是紧集。f是S×T上的连续实值函数。F是从G×H到G×H的集值映射,它在G×H上是闭的。如果下面两点成立:(1)对G×H中任意两点(u,v)和(x,y),(u,v)∈F(x,y),有f(u,v)≤f(x,y);(2)如果(x,y)不是f在G×H上的全局极小点,∀(u,v)∈F(x,y),有f(u,v) 本节利用图像恢复问题检验本文提出的优化设计方法是否能提高压缩感知系统的重构精度,以及是否能提升测量矩阵的稀疏性。总的来说,按如下方法进行检验:用文献[5,7,10,13,15]中的优化设计方法得到测量矩阵和稀疏字典;然后以其为初值,再用本文方法进行优化设计,得到新的测量矩阵(稀疏字典不变);最后,用两套测量矩阵和稀疏字典分别进行重构,比较重构效果。另外,用本文方法来处理标准压缩感知系统的测量矩阵和稀疏字典,即稀疏字典是用KSVD算法[21]从训练数据中学到的,而测量矩阵是高斯随机矩阵(即每个元素独立同分布地满足正态分布N(0,M-1),M为矩阵的行数)。下面分别阐述不同情形下的对比办法和实验结果。对所有情形,本文提出的方法采用参数T=1 500、Talter=15、β=0.5和σ=0.1。另外,所有代码均采用MATLAB(R2019b)编写,采用的笔记本电脑配置是Intel(R)Core(TM)i7⁃6500U处理器、主频2.50 GHz、内存8 GB。 首先,按如下方法获取训练数据:从LabelMe图像数据集[22]中随机选取400幅图像,再从每幅图像中无重叠地提取15个8×8的子块,把它们放到一起得到6 000个64维训练数据。再按如下方法获取测试数据:取10幅经典的512像素×512像素自然图像;把每幅无重叠地分割成一系列8×8的子块,得到4 096个64维测试数据。其次,用文献[5]中的优化设计方法从训练数据中得到测量矩阵和稀疏字典,采 用 的 参 数 是稀 疏 度6、迭 代 步 数100、初 始 测 量 矩 阵randn(M,N)和N×L的过完备离散余弦变换(Discrete cosine transform,DCT)矩阵形式的初始稀疏字典。再用本文提出的方法对得到的测量矩阵进行优化设计。最后,用两个测量矩阵分别对每一个测试数据进行测量,对理想测量值都添加高斯白噪声形式的测量噪声,使得信噪比等于10 dB。再用OMP算法和两套等效字典从测量值中恢复测试数据。对原始图像和重构图像,用峰值信噪比(Peak signal to noise ratio,PSNR)和结构相似性指标(Structural similarity index,SSIM)[23]评判重构效果,采用MATLAB软件内置命令PSNR和SSIM计算2个评判指标。另外,对测量矩阵,把绝对值小于10-4的分量认为是零。实验结果如表1所示,采用文献[5]方法得到的测量矩阵只包含0.520 8%的零元素,经本文方法处理后,这个比例升至57.552 1%。 表1 使用本文方法前后关于文献[5]中等效字典的重构效果Table 1 Reconstruction performance for equivalent dictionary in Ref.[5]with and without the proposed method 对采用文献[7]方法生成的测量矩阵和稀疏字典,按照针对文献[5]的比较办法,比较了在使用本文方法前后等效字典带来的重构效果和测量矩阵的稀疏性。文献[7]中的优化设计方法使用参数M=20、N=64、L=100、α=0.4、β=0.8、稀疏度4、迭代步数100、初始测量矩阵randn(M,N)和N×L的过完备DCT矩阵形式的初始稀疏字典。实验结果如表2所示。经本文方法处理后,采用文献[7]方法得到的测量矩阵的零元素占比由0.156 3%升至78.828 1%。 表2 使用本文方法前后关于文献[7]中等效字典的重构效果Table 2 Reconstr uction per for mance for equivalent dictionar y in Ref.[7]with and without the pr oposed method 对采用文献[10]方法生成的测量矩阵和稀疏字典,按照针对文献[5]的比较办法,比较在本文方法处理前后等效字典带来的重构效果和测量矩阵的稀疏性。但采用的训练数据不同。从LabelMe图像数据集中选取2 920幅图像,再从每幅图像中无重叠地提取400个8×8的子块,把它们放到一起得到1.168×106个64维训练数据。另外,文献[10]中的优化设计方法采用的参数是M=20、N=64、L=256、总的迭代步数10、字典学习的迭代步数、稀疏度4、ρ=15和随机选取L个训练数据整合在一起然后逐列单位化生成的初始稀疏字典。实验结果如表3所示,采用文献[10]方法得到的测量矩阵不包含零元素,而经本文方法处理后,这个比例升至84.921 9%。 表3 使用本文方法前后关于文献[10]中等效字典的重构效果Table 3 Reconstr uction per formance for equivalent dictionar y in Ref.[10]with and without the pr oposed method 因为文献[13]的优化设计方法和本文一样,在提高压缩感知系统重构精度的同时也提升了测量矩阵的稀疏性。所以本文准备对同样的测量矩阵Φ和稀疏字典Ψ,分别采用两种方法进行优化设计,然后分别用两套测量矩阵和稀疏字典进行重构,再比较重构效果和2个测量矩阵的稀疏性。采用如下办法生成Φ和Ψ:按照针对文献[5]的比较办法生成训练数据,然后用KSVD算法生成Ψ,采用的参数是M=20、N=64、L=100、稀疏度4、迭代步数50和N×L的过完备DCT矩阵形式的初始稀疏字典。再对KSVD算法的结果Ψ利用文献[13]提供的程序ZRE.m生成Φ(程序ZRE.m详见文献[24])。测试数据的生成以及重构过程则和针对文献[5]的比较办法中的一样。另外,文献[13]采用的参数是κ=20、λ=1.4和DCT矩阵形式的矩阵A。实验结果如表4所示。经本文方法处理后,按文献[13]中方法得到的测量矩阵的零元素占比由0.234 4%升至79.765 6%。 表4 使用本文方法前后关于文献[13]中等效字典的重构效果Table 4 Reconstruction performance for equivalent dictionary in Ref.[13]with and without the proposed method 对采用文献[15]方法生成的测量矩阵和稀疏字典,按照针对文献[5]的比较办法进行比较。不同的是训练数据、测试数据、添加测量噪声的方式和评判标准不一样。训练数据按如下方式生成:取10幅经典的512像素×512像素自然图像,滑动地把每幅图分割成一系列10×10的子块,把它们放在一起取其中的10%,得到25 301个100维训练数据。测试数据由人工生成。利用KSVD算法从训练数据中得到一个N×N维的稀疏字典Ψ,采用的参数是稀疏度4、迭代步数50和DCT正交矩阵形式的初始稀疏字典。测试数据x按如下方式生成:生成稀疏向量α(稀疏度是4,支撑集服从等概率分布,非零分量独立同分布地服从(-1,1)上的均匀分布),计算x=Ψα。总共生成3 000个这样的向量。对测量值逐分量地加上服从正态分布N(0,0.01)的噪声。因为测试数据不是自然图像,所以用全体测试数据及其重构结果的均方误差来评判重构效果。用MATLAB软件的内置命令immse计算均方误差(Mean square error,MSE)。另外,文献[15]中的优化设计方法采用的参数是:η=1.2、ρ=0.5、β=2、T=15、TAM=1000、M=20、N=L=100、初始测量矩阵和KSVD算法生成的初始稀疏字典Ψ。实验结果如表5所示。对10幅图像,按文献[15]中方法得到的测量矩阵都不包含零元素,而经本文方法处理后,测量矩阵的零元素占比(对应表5中从上到下的顺序)依次为76.700 0%、77.450 0%、80.250 0%、76.100 0%、78.250 0%、79.850 0%、78.500 0%、76.900 0%、72.700 0%和80.100 0%。 表5 使用本文方法前后关于文献[15]中等效字典的重构效果Table 5 Reconstruction performance for equivalent dictionary in Ref.[15]with and without the proposed method 按照针对文献[5]的比较办法进行比较,只是生成待比较的测量矩阵和稀疏字典的方式不同。用KSVD算法从训练数据中得到稀疏字典,采用的参数是M=12、N=64、L=256、迭代步数50、稀疏度6和N×L维的过完备DCT矩阵形式的初始稀疏字典;而测量矩阵是高斯随机矩阵。实验结果如表6所示,生成的标准压缩感知系统的测量矩阵不包含零元素,而经本文方法处理后,则包含29.166 7%的零元素。 表6 使用本文方法前后关于标准压缩感知系统中等效字典的重构效果Table 6 Reconstruction performance for equivalent dictionary in standard compressed sensing system with and without the pr oposed method 从2.4节实验处理的10幅图像中选择4幅原始图像。把每幅原始图像、利用文献[13]方法设计的测量矩阵和稀疏字典得到的重构图像、利用已有稀疏字典和本文方法处理后的测量矩阵得到的重构图像,以及上述3幅图像的某个共同细节部分进行并列展示,具体如图1~4所示。 图1 图像“lena”及其重构结果Fig.1 Image“lena”and its reconstruction 从本节所有数值实验可以看到,对按照文献[5,7,10,13,15]生成的测量矩阵和稀疏字典,以及标准压缩感知系统的测量矩阵和稀疏字典,应用本文提出的方法进行优化得到的新测量矩阵搭配上已有稀疏字典能够在图像恢复阶段带来更高的信号重构精度,同时还能显著提高测量矩阵中的零元素占比。 图2 图像“jetplane”及其重构结果Fig.2 Image“jetplane”and its reconstruction 图3 图像“boats”及其重构效果Fig.3 Image“boats”and its reconstruction 图4 图像“bridge”及其重构效果Fig.4 Image“bridge”and its reconstruction 本文利用最优化方法提出了一种压缩感知等效字典的优化设计方法。提出的最优化问题在使等效字典的Gram矩阵逼近某类特定Gram矩阵的同时,要求测量矩阵满足某种基于L1范数的不等式约束。然后,根据交替投影算法框架提出了收敛的求解算法。数值实验表明,就图像恢复问题而言,对采用一些经典的以及新提出的优化设计方法得到的测量矩阵和稀疏字典,以及标准压缩感知系统的测量矩阵和稀疏字典,求解提出的最优化问题,得到的新测量矩阵搭配上已有稀疏字典能有效提高信号重构精度,同时显著提升测量矩阵的稀疏性。 相较同类方法,本文提出的方法着重关注测量矩阵的稀疏性对后续信号重构效率的影响,并首次利用L1范数对测量矩阵赋予稀疏性。利用本文方法优化设计压缩感知的等效字典,可在信号重构阶段获得精度与效率的双提高。为了能够利用本文方法优化设计大规模等效字典,下一步将会研究求解最优化问题(4)的更加高效的迭代算法,或者是最优化问题(4)的闭合形式解的求法。 附录 现在取K=max{K1,K2}。则∀k>K(k是正整数),有2 数值实验
2.1 关于文献[5]的数值实验

2.2 关于文献[7]的数值实验

2.3 关于文献[10]的数值实验
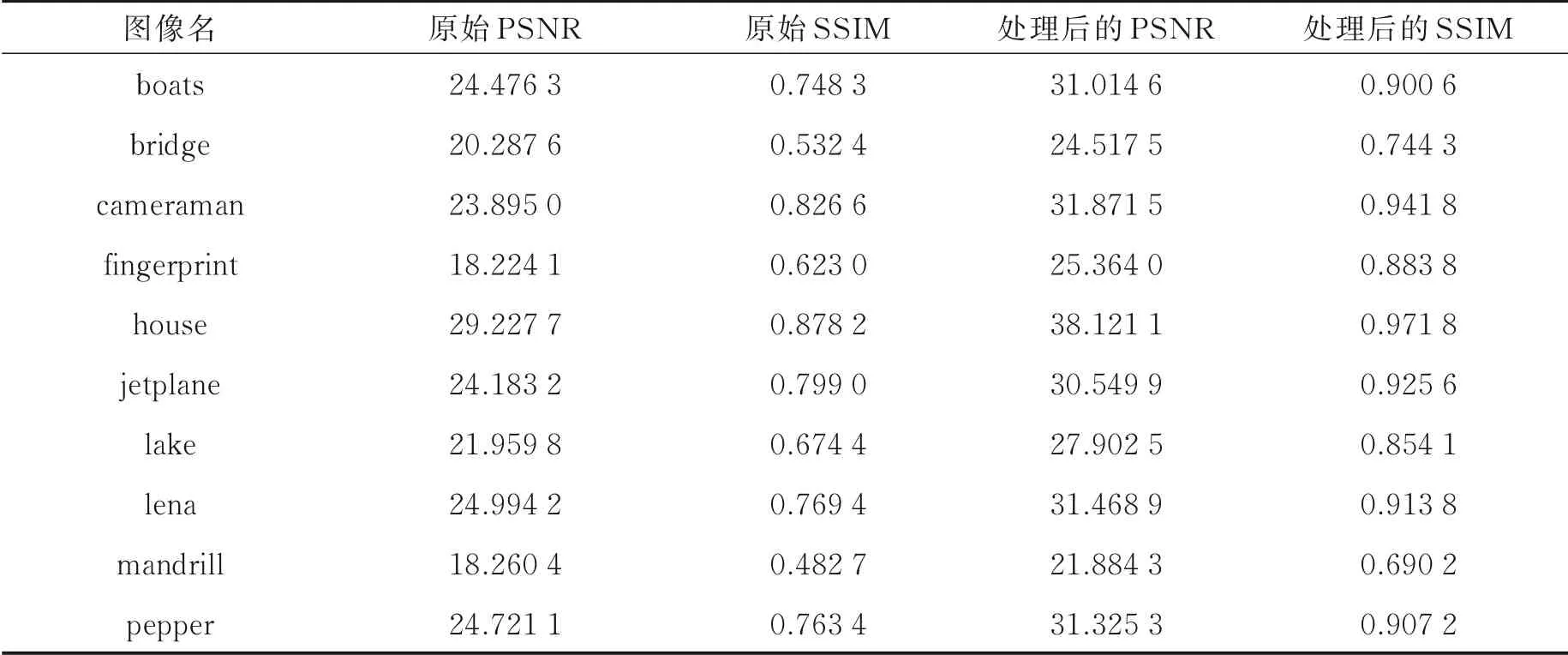
2.4 关于文献[13]的数值实验
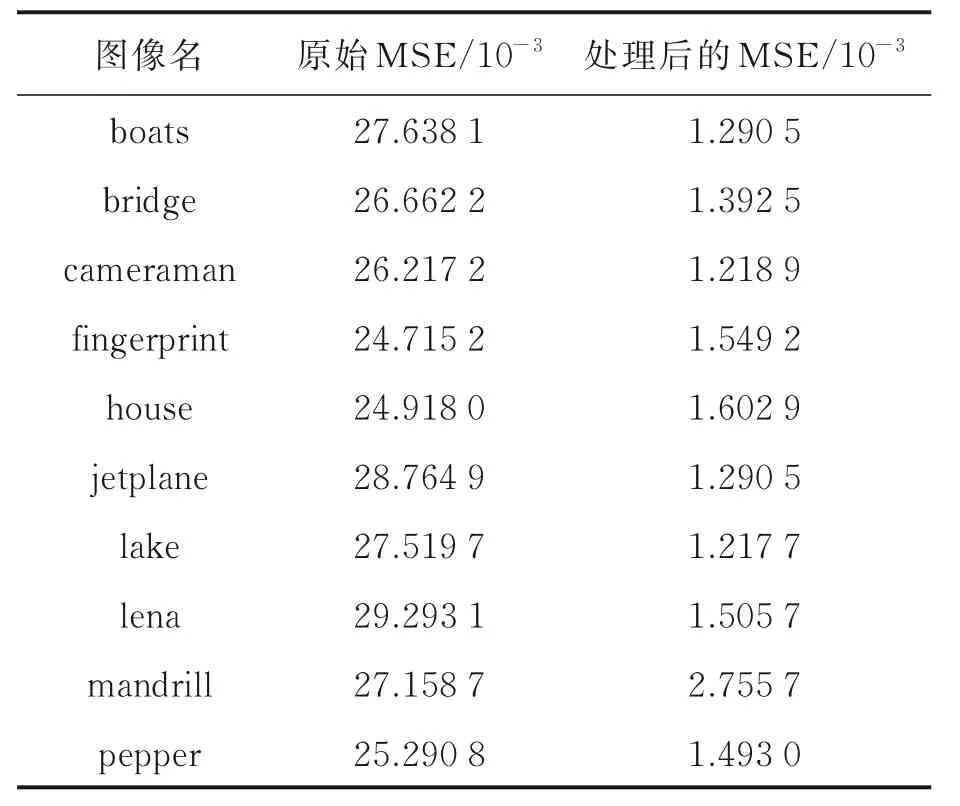
2.5 关于文献[15]的数值实验
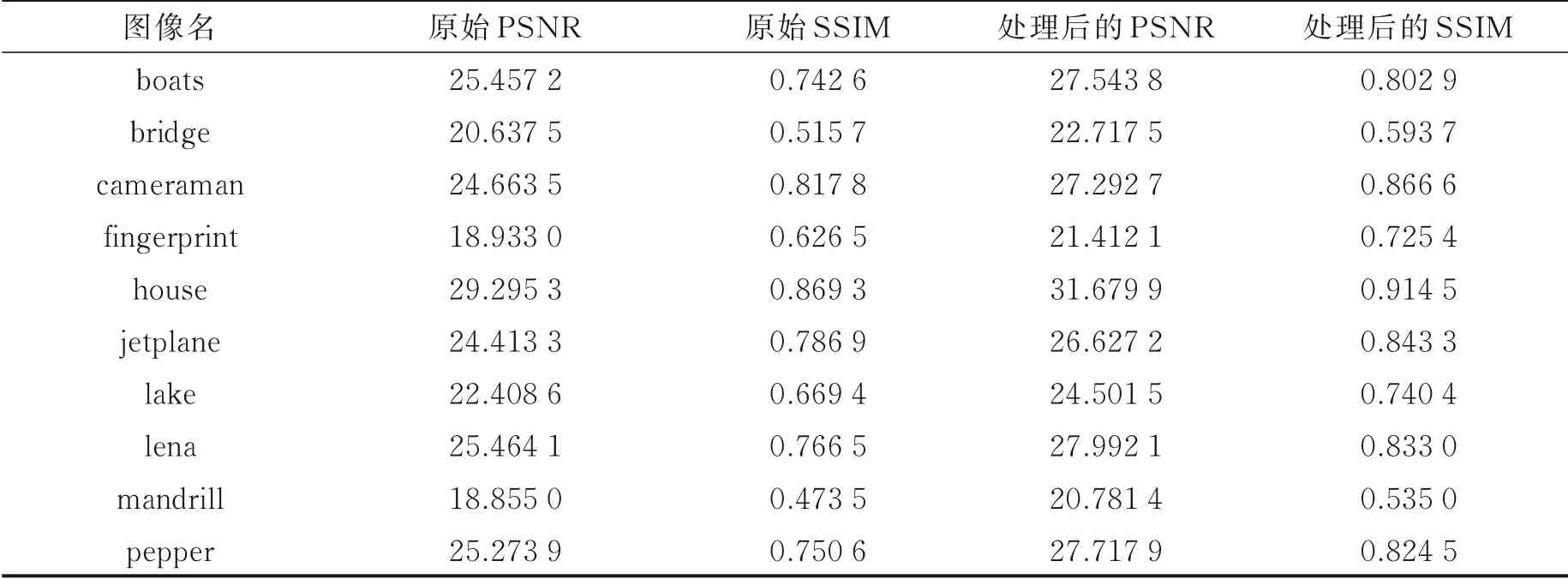
2.6 关于标准压缩感知系统的数值实验
2.7 重构效果的进一步展示




3 结束语