基于蜂窝结构的改进混合无线传感器网络覆盖优化算法

张清国，张勇，张伟，席瑞洁

（1.华中师范大学 计算机学院，武汉 430079；2.华中科技大学 计算机科学与技术学院，武汉 430074）

0 概述

无线传感器网络（Wireless Sensor Network，WSN）广泛应用于环境监控、反恐救灾、军事、医疗健康、动物跟踪等领域［1］。传统的静态WSN 完全由固定传感器组成，所有的传感器在部署完之后位置都保持不变，只能通过将网络中部署的冗余传感器从睡眠状态唤醒的方法来完成覆盖洞修补，该覆盖洞修补方式需要监控区域能被传感器网络全覆盖，而这在敌对或恶劣的自然环境中（如战场、森林火场等）是不切实际的，在这些场景中很难对WSN 进行人工部署。通过飞机撒播、火箭弹射等随机部署方式，在遇到障碍物时即使提高节点的部署密度，也难以一次就将所有传感器部署到适当的位置，极易造成节点分布过密或过疏从而形成覆盖重叠区和覆盖盲区，难以实现区域全覆盖。

近年来，研究人员提出由固定传感器和移动传感器组成的混合无线传感器网络（Hybrid Wireless Sensor Network，HWSN）［2-3］，与完全由固定传感器组成的静态WSN 不同，HWSN 可以对移动传感器进行重新部署［4-5］，修复传感器网络由于节点分布不均或节点因能量耗尽而失效等原因形成的覆盖洞［6-7］，从而优化网络覆盖性能［8-10］。

针对HWSN 的覆盖控制问题，学术界进行了大量研究。文献［11-13］提出基于虚拟力的WSN 覆盖算法，但该算法容易陷入局部最优，导致网络覆盖优化失败。由于覆盖问题是NP-难问题［14］，因此研究人员将各种智能算法应用于HWSN 覆盖控制任务，如鱼群算法［15-17］、遗传算法［18-20］、差分演化算法［21-22］、蚁群算法［23-25］、粒子群算法［26-27］等，且取得了较好的效果，但是，这些方法存在的最大问题是算法时间复杂度高，计算量大，收敛速度慢，有时甚至收敛于局部最优解，导致覆盖优化失败。

在HWSN 中，能耗主要来源于2 个方面，即相邻传感器之间的通信以及移动传感器节点的机械运动。文献［28］指出，将移动传感器节点移动1 m 所消耗的能量是传感器发送一个消息所消耗能量的300 倍，因此，HWSN 的能耗主要体现在重新部署移动传感器位置时移动传感器所耗费的能量。本文用移动节点的平均移动距离（Average Moving Distance，AMD）作为移动传感器机械运动能耗的度量标准，因此，优化移动节点的AMD 具有十分重要的意义。文献［29］提出一种基于蜂窝结构的HWSN 覆盖优化算法HWSNBCS，根据移动节点和其倍感知半径范围内固定节点间的位置关系，基于蜂窝结构和漏洞修补策略对移动节点进行重新部署，以改善网络的覆盖性能。该算法包括2 个阶段：第一阶段基于蜂窝结构计算每个移动传感器的候选目标位置，其中，算法给出了4 种情况下移动节点的移动方案；第二阶段对所有移动节点的候选目标位置进行进一步优化，确定移动节点的最终目标位置。算法通过移动传感器移动距离优化算法来减少移动传感器的AMD，从而降低移动节点的能耗，确定移动节点的最终目标位置。HWSNBCS 算法能显著改善网络的覆盖性能，且执行效率较高，但算法第二阶段的移动传感器移动距离优化算法只是通过简单地将移动传感器的候选目标位置两两互换，以寻找移动节点移动距离的可能优化结果，这种启发式方法得到的解不一定是最优解，本文将在第2 章对其进行例证和分析。

本文将HWSN 移动节点移动距离之和最小化问题转化为二分图最优匹配问题，用带权二分图匹配算法KM（Kuhn-Munkres）对文献［29］中的HWSNBCS算法进行改进，具体地，利用KM 算法对HWSNBCS算法第一阶段移动节点的移动距离进行优化，在保持算法第一阶段网络覆盖率不变的前提下，减少移动节点的平均移动距离以及单个移动节点的最大移动距离，从而降低系统能耗。

1 HWSNBCS 算法

设由n个传感器节点S=｛s1，s2，…，sn｝组成的HWSN 随机分布在二维平面区域A中。为了讨论方便，对HWSN 作如下假设：

1）每个传感器都知道自己的位置信息。

2）所有传感器的通信半径Rc相同，感知半径R也相同，且Rc=2R。

3）在区域A中存在一个Sink 节点，该节点负责完成算法的移动距离优化。

在分析HWSNBCS 算法之前先介绍算法中的2 个概念：

定义1设R为传感器sa的感知半径，以传感器节点sa为圆心、以R为半径的圆周称为节点sa的邻接蜂窝节点轨迹圆（Neighboring Cellular Node Locus Circle，NCNLC）［29］。

定义2若移动节点ma在固定节点sa的NCNLC上，则称sa的NCNLC为ma的候选蜂窝节点轨迹圆（Candidate Cellular Node Locus Circle，CCNLC）［29］。

1.1 基于蜂窝结构的节点移动策略

HWSNBCS 算法第一阶段给出4 种情况下移动传感器的移动方案：

1）若移动传感器ma的NCNLC 内没有固定传感器，则ma不需要移动［29］。如图1 所示，虚线圆周是移动传感器ma的NCNLC，由于ma的NCNLC 内没有固定传感器，因此ma不需要移动。

图1 移动节点ma的NCNLC 内无固定节点的情况Fig.1 No static node within the NCNLC of the mobile node ma

2）若移动传感器ma位于某个固定传感器sa的NCNLC 内，记sa的NCNLC 为⊙sa，则ma沿直线sama移动到⊙sa上距ma较近的点［29］。如图2所示，ma沿直线sama移动到⊙sa上的A点。

图2 移动节点ma在某个固定节点NCNLC 内的移动方案Fig.2 Mobile scheme of mobile node ma in NCNLC of a fixed node

3）当移动传感器ma位于某个固定传感器的NCNLC 内，且ma有一个CCNLC 时，ma移动到CCNLC 与固定节点的NCNLC 的交点中距离ma较近的点［29］。如图3 所示，ma有一个CCNLC，为sa的NCNLC，记为⊙sa，同时ma位于sb的NCNLC 内，记sb的NCNLC 为⊙sb，则ma移动到⊙sa与⊙sb的2 个交点中距离ma较近的B点［29］。

图3 移动节点ma只有一个CCNLC 时的移动方案Fig.3 Mobile scheme of mobile node ma when ma has only one CCNLC

4）若移动传感器ma位于某个固定传感器的NCNLC 内，且ma有2 个CCNLC 时，ma移动到3 个固定传感器的NCNLC 的交点中距离ma较近的外层交点［29］。如图4 所示，ma有2 个CCNLC，分别是固定节点sa、sb的NCNLC，且ma位于固定节点sc的NCNLC内，则ma移动到这3 个NCNLC 的交点中距离ma最近的最外层交点A［29］。

图4 移动节点ma有2 个CCNLC 时的移动方案Fig.4 Mobile scheme of mobile node ma when ma has two CCNLC

1.2 节点移动距离优化

HWSNBCS 算法第二阶段通过对移动节点的移动距离进行优化，从而确定移动节点的最终目标位置［29］。通过将移动传感器的候选目标位置两两交换，寻找移动节点移动距离的可能优化结果，其原理如图5 所示。假设Pa、Pb分别为移动节点ma、mb的候选目标位置，如果|maPa|+|mbPb|＞|maPb|+|mbPa|，则交换ma、mb的候选目标位置Pa、Pb。

图5 HWSNBCS 算法移动节点移动距离优化方案Fig.5 Optimization scheme of moving distance of mobile nodes in HWSNBCS algorithm

1.3 算法描述

基于蜂窝结构的HWSN 覆盖优化算法HWSNBCS 描述如下：

算法1HWSNBCS 算法

输入目标区域A，初始节点集合S=｛s1，s2，…，sn｝，其中s1，s2，…，sm为移动节点，其余为固定节点

输出移动节点重新部署的目标位置P=｛p1，p2，…，pm｝，其中p1，p2，…，pm分别为移动节点s1，s2，…，sm的新目标位置

步骤1Fori：=1 tomdo

对移动传感器节点mi，根据图1～图4 所示的4 种情况，计算其候选目标位置Pi。

步骤2随机选取2 个移动传感器ma、mb，设其初始位置分别为Pa0、Pb0，当前候选目标位置分别为Pa1、Pb1。如果|Pa0Pa1|+|Pb0Pb1|＞|Pa0Pb1|+|Pb0Pa1|，则Pa1↔Pb1，其中|·|表示节点之间的欧式距离。

步骤3重复步骤2，直至整个HWSN 的AMD不能减少为止。

步骤4输出集合P。

显然，步骤2～步骤3 不会改变整个网络的覆盖率，但可减少移动节点的AMD，从而进一步优化移动节点的布局。

2 基于蜂窝结构的改进HWSN 覆盖控制算法

HWSNBCS 算法的步骤2 简单地将移动节点的候选目标位置两两互换，以寻找移动节点移动距离的可能优化结果，这是一种启发式方法，得到的解不一定是最优解。图6 所示为一个简单的带权二分图，Pa、Pb、Pc分别为移动传感器ma、mb、mc的候选部署位置，ma、mb、mc分别到Pa、Pb、Pc的距离如图中所示。不失一般性，移动传感器按照ma、mb、mc的顺序依次选择候选部署位置，将会选择Pb、Pa、Pc分别作为ma、mb、mc的目标位置，3 个移动节点移动距离之和为|maPb|+|mbPa|+|mcPc|=3+5+8=16，比原来的|maPa|+|mbPb|+|mcPc|=5+4+8=17 仅减少1，但实际上最短距离之和为|maPc|+|mbPb|+|mcPa|=4+4+4=12。因 此，HWSNBCS 算法中移动节点移动距离优化方案得到的解并非全局最优解，移动节点的移动距离还可以进一步优化。

图6 简单的带权二分图Fig.6 Simple weighted bipartite graph

HWSNBCS 算法中距离优化的实质是寻找移动传感器节点初始位置与其候选目标位置之间的最优匹配，使得移动节点移动距离之和最小化。为此，本文采用带权二分图最优匹配算法KM 来解决这一匹配问题，以实现对HWSNBCS 算法的改进。

2.1 算法描述

KM 是用于求解带权二分图最优匹配问题的经典算法。本文通过构造带权二分图，将HWSN 移动传感器移动距离优化问题转化为二分图最优匹配问题。设HWSN 中移动节点s1，s2，…，sm的初始位置为Q=｛q1，q2，…，qm｝，qi为移动节点si的初始位置，通过HWSNBCS 算法步骤1 得到的移动节点候选目标位置为P=｛p1，p2，…，pm｝，pi为移动节点si的候选目标位置。构造带权二分图G=（V，E），顶点集V=Q∪P，边集E=｛（u，v，wuv）|u∈Q，v∈P，wuv=-|uv|｝，wuv表示边（u，v）的权值，为顶点u、v之间欧式距离的相反数。用KM 算法求出图G的最优匹配，即可得到移动节点移动距离之和最小化的目标位置。本文所提基于蜂窝结构的改进HWSNBCS算法（IHWSNBCS）描 述如下：

算法2IHWSNBCS 算法

输入移动节点s1，s2，…，sm初始位置Q，通过HWSNBCS 算法步骤1 得到的候选目标位置P

输出集合Q与集合P移动距离之和最小的匹配结果

步骤1定义初始可行顶点标记L：

步骤2设El={（qi，pj）|L(qi)+L(pj)=}，Gl=(V，El}，设X为Gl的一个匹配。若Q中每个点都是X的饱和点，则X就是所求的移动传感器移动距离之和最小的匹配结果，计算结束；否则，取X的非饱和点qi∈Q，令A=｛qi｝，B=Ø，A、B为2 个集合。

步骤3令(A)={pj|qi pj∈El，qi∈Q，pj∈P}，若NGL(A)=B，则Gl没有最优匹配，转步骤4；否则，转步骤5。NGL(A)⊆P是与A中节点邻接的节点集合。

步骤4调整可行顶点标记。令d=min{L（qi）+L（pj）-|qi∈A，pj∈P-B}，按式（2）修改可行顶点标记：

根据L'计算EL'及GL'，令L=L'，GL=GL'，转步骤2。

步骤5取p∈(A) -B，若p是X的饱和点，转步骤6；否则，转步骤7。

步骤6设qp∈X，令A=A∪｛q｝，B=B∪｛p｝，转步骤3。

步骤7GL中的（u，p）路是X增广路，记为path，并令X=X⊕path，转步骤2，最终求得X。

从IHWSNBCS 算法可以看出，其输入和HWSNBCS 算法第二阶段的输入完全一样，但HWSNBCS 算法第二阶段采用启发式方法，而IHWSNBCS 算法采用全局优化方法，即KM 算法，KM 算法的正确性早已得到证明，因此，本文IHWSNBCS 算法能得到一个较好的解。

IHWSNBCS 算法并不改变HWSNBCS 算法的网络覆盖率，仅改变HWSNBCS 算法中移动节点的平均移动距离，这是因为IHWSNBCS 算法只对HWSNBCS 算法移动节点的初始位置和目标位置进行重新匹配，在整个HWSN 中，固定节点的位置没有发生变化，因此，其监测区域也没有变化，相比HWSNBCS 算法而言，IHWSNBCS 中移动节点整体监测的区域实际上也没有发生变化，变化的只是单个传感器的监测区域。因此，IHWSNBCS 算法传感器节点的监测区域与HWSNBCS 算法相同，即IHWSNBCS 算法并未改变HWSNBCS 算法的网络覆盖率。

2.2 复杂度分析

首先分析IHWSNBCS 算法的时间复杂度。IHWSNBCS 的输入是运行HWSNBCS 算法步骤1 的输出，其时间复杂度为O（m（n-m））［29］。IHWSNBCS 算法中的KM 算法通过不断寻找从未匹配点qi∈Q出发的可增广路，以扩充当前的匹配情况，执行次数为m，利用深度优先搜索可增广路，其时间复杂度为O（m2），即KM 算法的时间复杂度为O（m3）［30］。因 此，IHWSNBCS 算法的时间复杂度为O（mn+m3），高于HWSNBCS 算法的时间复杂度O（mn）［29］，原因是IHWSNBCS 算法要调用KM 算法，提高了运算复杂度。

然后分析IHWSNBCS 算法的空间复杂度。IHWSNBCS 算法和HWSNBCS 算法的内存消耗主要来源于移动节点的初始位置和候选目标位置，因此，空间复杂度均为O（m），改进算法并未增加空间开销。

最后分析IHWSNBCS 算法的通信复杂度。为了得到IHWSNBCS 算法的输入而运行HWSNBCS算法的步骤1，其通信开销为O（m）［29］。IHWSNBCS算法中KM 算法的输入是各移动传感器节点的初始位置和候选目标位置，对于给定的目标监测区域A，设移动节点发送数据包到Sink 节点的平均跳数为h，则移动节点将其初始位置信息和候选目标位置信息发送到Sink 节点的通信开销为O（mh），Sink 节点将KM 算法计算出的各移动节点的最终目标位置信息发送至各移动节点的通信开销为O（mh）。因此，IHWSNBCS 算法的总通信开销为O（mh），高于HWSNBCS 算法的通信开销O（m）［29］，其原因也是因为调用KM 算法时需要向Sink 节点发送消息。

3 实验结果与分析

为了评估本文算法的性能，在Win 10 下用Visual studio 2019 进行仿真，仿真场景为一个125 m×125 m 的矩形区域，其中随机分布着若干传感器，传感器的感知半径和通信半径分别为10 m 和20 m。

为了更好地评价算法性能，本文引入式（3）所示的ΔCov-Dist 指标：

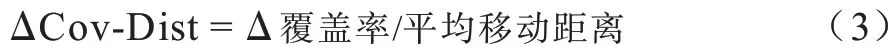
其中：平均移动距离是HWSN 中所有移动节点移动距离的平均值，平均移动距离越小，系统因重新部署移动传感器节点的总能耗越低；ΔCov-Dist 是单位移动距离下网络覆盖率的变化，为网络覆盖率的变化与移动节点平均移动距离的比值，ΔCov-Dist 越大，移动节点移动相同距离时网络覆盖率提升越大，HWSN 能效越高。

图7（a）所示为一个由40 个固定传感器和20 个移动传感器所组成的HWSN，对图7（a）所示的HWSN 分别运行HWSNBCS 和IHWSNBCS 算法，得到图7（b）、图7（c）所示的实验结果，图中小空心圆表示传感器节点，深色填充大圆表示移动传感器的感知区域，浅灰色填充大圆表示固定传感器的感知区域，线段表示移动传感器初始位置和目标位置之间的直线距离，线段越长，表示移动传感器移动距离越远。从图7 可以看出，图7（a）中传感器分布不均，区域中有明显的覆盖洞，其网络覆盖率为65.29%。图7（b）、图7（c）通过对移动传感器重新部署，网络的覆盖性能明显改善，其覆盖率达到83.39%。虽然图7（b）和图7（c）的覆盖率一样，但图7（b）中移动传感器的AMD 为35.45 m，而图7（c）中移动传感器的AMD 为21.67 m，前者AMD 减少了38.87%，显然，本文IHWSNBCS 算法中移动节点的AMD 更短。图7（b）的ΔCov-Dist 为0.51，图7（c）的ΔCov-Dist 为0.84，后者为前者的1.64 倍，说明网络能效更高。此外，从图7 中还可以看出，图7（c）中长度较长的线段数量比图7（b）中少，且最长线段的长度比图7（b）中短，说明本文算法单个节点的最大移动距离也大幅缩短，单个节点的最大移动距离过大，会导致该节点因能量消耗过快而成为失效节点，从而形成覆盖盲区，影响网络的覆盖性能。

图7 包含60 个节点的HWSN 在2 种算法下的运行结果Fig.7 Running results of HWSN with sixty nodes under two algorithms

图8 所示为一个由56 个固定传感器和24 个移动传感器所组成的HWSN，其初始覆盖率为75.25%。对图8 所示的HWSN 分别运行HWSNBCS 和IHWSNBCS 算法，得到表1 所示的实验结果。从表1可以看出，通过对部分移动节点进行重新部署，2 种算法都大幅提高了网络覆盖率，改善了网络的覆盖性能。虽然本文IHWSNBCS 算法并不改变HWSNBCS 算法的覆盖率，但IHWSNBCS 算法移动节点的平均移动距离更小，与HWSNBCS 算法相比减少了43.28%，说明达到相同的覆盖性能，本文算法移动节点的能耗更小，且单个移动节点的最大移动距离更短，比HWSNBCS 算法减少66.58%，这将降低单个节点因能量过早耗完而失效的概率，从而有助于延长整个传感器网络的生命周期。此外，IHWSNBCS 算法的ΔCov-Dist 指标是HWSNBCS 算法的1.76 倍，说明前者能效更高。

图8 包含80 个节点的HWSNFig.8 HWSN with 80 nodes

表1 包含80 个节点的HWSN 在2 种算法下的运行结果Table 1 Running results of HWSN with eighty nodes under two algorithms

在HWSN 传感器总数保持不变的情况下，改变移动传感器的比例，分别运行HWSNBCS 和IHWSNBCS 算法，实验中移动节点均为随机选取。表2 所示为2 种算法在不同移动节点比例下的覆盖率和单个节点最大移动距离。从表2 可以看出：随着移动传感器节点比例的提升，通过对更多的移动节点进行重新部署，网络的覆盖率逐渐提升，但本文算法单个移动节点的最大移动距离比HWSNBCS 算法减少了22.65%～66.58%，这将大幅减少单个移动节点重新部署的最大能耗，降低节点因能量过早耗完而失效的概率。

表2 不同移动节点比例下2 种算法的运行结果Table 2 Running results of two algorithms under different mobile node proportions

图9 所示为2 种算法移动节点平均移动距离在不同移动节点比例下的变化情况。从图9 可以看出：随着移动节点比例的增加，有更多的移动节点被重新部署，本文IHWSNBCS 算法移动传感器的AMD 逐渐减少，其AMD 比HWSNBCS 算法中的AMD 小很多，这是因为对于移动传感器移动距离最小化问题，本文使用的KM 算法能够得到全局最优解，而HWSNBCS 算法得到的是局部最优解，因此，HWSNBCS 算法的AMD 比本文算法大，且随着移动传感器比例的增大，HWSNBCS 算法移动节点的AMD 变化趋势也没有IHWSNBCS 算法明显。

图9 2 种算法在不同移动节点比例下的平均移动距离Fig.9 Average moving distance of two algorithms under different mobile node proportions

图10 所示为2 种算法的ΔCov-Dist 指标在不同移动节点比例下的变化情况。从图10 可以看出，本文算法的ΔCov-Dist 指标明显大于HWSNBCS 算法，这是由于在覆盖率变化相同的情况下，本文算法的平均移动距离更小，因而通过式（3）计算出的ΔCov-Dist 更大，能效更高。

图10 2 种算法在不同移动节点比例下的ΔCov-DistFig.10 ΔCov-Dist of two algorithms under different mobile node proportions

对一个由56 个固定节点和24 个移动节点组成的HWSN 分别运行标准遗传算法、粒子群算法、HWSNBCS 算法和IHWSNBCS 算法，实验结果如表3 所示。其中，粒子群算法和遗传算法均以最大化网络覆盖率为优化目标，在达到与HWSNBCS 以及IHWSNBCS 相同的覆盖率时算法停止。粒子群算法和遗传算法各运行50 次，取其平均值，HWSNBCS 和IHWSNBCS 算法各运行1 次。实验中移动节点的初始能量为1 500 J，移动节点每移动1 m所消耗的能量为30 J。当重新部署某个移动节点时，如果其需要耗费的能量大于初始能量，则认为该节点失效。从表3 可以看出，本文算法的失效节点数明显少于其他3 种算法，因此，其网络生命周期会更长。

表3 4 种算法的失效移动节点数对比Table 3 Comparison of the number of failed mobile nodes of four algorithms

4 结束语

本文提出一种基于蜂窝结构的改进HWSN 覆盖优化算法IHWSNBCS。将HWSN 中移动传感器的移动距离优化问题转化为二分图匹配问题，然后利用带权二分图匹配算法KM 计算匹配问题的最优解，从而实现对HWSNBCS 算法的优化。实验结果表明，IHWSNBCS 算法可在保持原有HWSNBCS 算法网络覆盖率不变的前提下，大幅减少移动节点的平均移动距离以及单个移动节点的最大移动距离，同时提高系统能效，延长网络的生命周期。下一步将在单个移动节点的最大移动距离约束下优化节点的位置部署，从而提高网络覆盖性能。