Helmholtz方程反问题的PINNS解法*

戴卫杰，张 文,†，徐会林，夏 贇

(1.东华理工大学 理学院，南昌 330013；2.赣南师范大学 数学与计算机科学学院，江西 赣州 341000)

1 引言

Helmholtz方程常常用来描述电磁散射、声波散射和水波传播等物理现象，在电磁辐射、地震学和声学等领域具有广泛应用，如何计算Helmholtz方程的解成为众多学者讨论的热点问题.Wang[1]对未知扰动部分进行修正，最后反演出Helmholtz方程的波数.Wang[2-3]等人用了局部奇异边界法和局部结点法对二维和三维Helmholtz方程正反问题进行了求解，Marin[4]等人研究了基本解方法在二维Helmholtz型方程Cauchy问题中的应用,并且使用了一阶Tikhonov泛函进行正则化，Liu[5]用了一种新的Trefftz方法对三维修正Helmholtz方程Cauchy反问题进行求解.人工神经网络最早由数理逻辑学家Pitts和McCulloch于1943年提出，经过一段时间完善之后，Lee[6]、Wang[7]、Yentis[8]将其用来求解偏微分方程，随后Lagaris[9]等人通过训练网络求解微分方程，其核心思路是将微分方程的初始解划分为2部分：第1部分用来满足边界条件，第2部分用来搭建人工神经网络.

最近，Hinton[10]基于大批量训练数据提出深度学习概念，在大数据领域取得巨大反响，为了弥补数据量巨大的缺陷，Karniadakis[11]等提出了深度学习算法:内嵌物理机理神经网络(Physics-informed neural networks，缩写为PINNs)，将微分方程的初边值条件和测量数据放在损失函数当中去训练，最后得到微分方程的解和参数的识别结果.但是，对于PINNs来说，最小化损失的方法一般采用梯度下降法，但是由于损失函数一般来说都是非凸的，所以梯度下降法可能会陷入局部最小值而达不到全局最小，而Kingma[12]提出的Adam算法能够得到全局最优解很好的解决了这个问题.Song[13]等人利用PINNs提出了求解Helmholtz方程的通用方法，Gorbachenko[14]等人提出了求解反问题的方法.

近年来，PINNs发展出了许多版本，比如cPINNs[15]、gPINNs[16]、fPINNs[17]等，而Jagtap[18]等通过将PINNs中的激活函数修改为自适应激活函数，大大的加快了收敛速度，在理论层面，Shin[19]等针对椭圆型和抛物型偏微分方程，证明了经过PINNs训练后得到的网络一致收敛于偏微分方程的解.

本文的创新点在于通过PINNs方法求解出Helmholtz方程近似解U的同时，根据附加信息对未知参数p和k进行同步反演；此外，由于PINNs方法中引进的偏微分残差项起到了正则化作用，于是无需额外采用正则化方法，也能求解不适定问题.

本文首先介绍了PINNs结构，然后对Helmholtz方程正问题进行求解，最后针对Helmholtz方程中的未知参数p和波数k进行了反演求解.

2 PINNs结构

M(σ)∶=span{σ(w.x+b)∶w∈d,b∈}

(1)

在Cm1,…,ms(d)∶=d)是稠密的.

该定理告诉我们,对于任意函数,只要神经网络足够大,神经元数量足够多或者层数足够深,神经网络可在精度范围内逼近函数及其m阶导函数.下面我们考虑用神经网络去求解方程的解.

考虑如下Helmholtz方程

(2)

首先，我们建立深度神经网络n(x,y;θ)去逼近方程(2)的解U,定义偏微分方程的残差F(x,y;θ)作为输出,即：

(3)

其中,偏导数由自动微分求得.定义边界条件残差Lub(θ)、偏微分方程残差Lf(θ,p,k2)和数据残差Lu(θ)分别为：

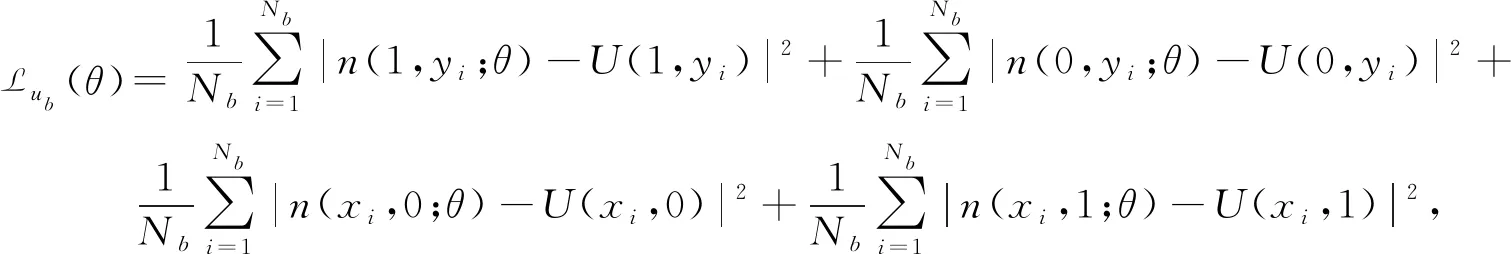
(4)

(5)

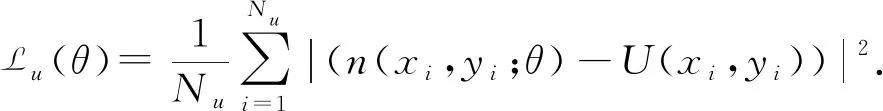
(6)

损失函数的训练集分为3部分，第1部分为边界条件的采样点集，第2部分为对偏微分方程残差进行的配置点集(配置点集一般有两种选取方式：类网格点选取方式和伪随机离散取点方式)，第3部分为测量数据的采样点集，该部分用于参数识别的反问题.Nb,Nf,Nu分别为边界点、方程配置点和测量数据的训练集大小，则损失函数定义为：

L(θ,p,k2)=Lub(θ)+Lf(θ,p,k2)+Lu(θ).

(7)

注由损失函数的结构可以看出，偏微分残差项起到了正则化作用，增强了网络泛化能力.另外，通过自动微分构建偏微分方程残差并将其引入到损失函数，实际上是将该偏微分方程表示的物理规律嵌入到深度网络，为PINNs方法的关键含义.

最后，我们用优化算法(如梯度下降法)训练深度神经网络n(x,y,θ)和方程中参数p,k2，使得损失函数L(θ,p,k2)达到最小.为避免因非凸优化引起的达不到全局最优问题，我们采用Adam算法更新参数，具体算法如下：

其中，β1,β2分别为一阶矩和二阶矩的指数衰减率，α为学习率，通常取β1=0.9,β2=0.999,α=0.001.

3 PINNs解Helmholtz方程正反问题

3.1 正问题的求解算法

(8)

取均方误差的和作为损失函数

(9)

算法2: PINNS解Helmholtz方程正问题算法步骤1: 构建一个深度神经网络n(x,y,θ)去近似真解U;步骤2: 初始化参数θ,也就是神经网络的权w和偏差b;步骤3: 选取边界点训练集和方程配置点的训练集大小;步骤4: 利用自动微分技术求出微分方程残差F(x,y;θ)步骤5: 根据边界条件和步骤3得到的方程残差得到损失L(x,y,θ);步骤6: 利用Adam算法对神经网络参数θ进行训练来最小化L(x,y,θ);步骤7: 直到损失L(x,y,θ)达到我们想要的精度或者达到最大训练步数停止得到最终的近似解n(x,y;θ*).

我们选取一个100×100的网格作为我们的训练点集，训练过程中损失函数L(x,y,θ)随迭代步数的变化如图1所示.

图1 损失函数随迭代步数变化图

图2 精确解和近似解对比图

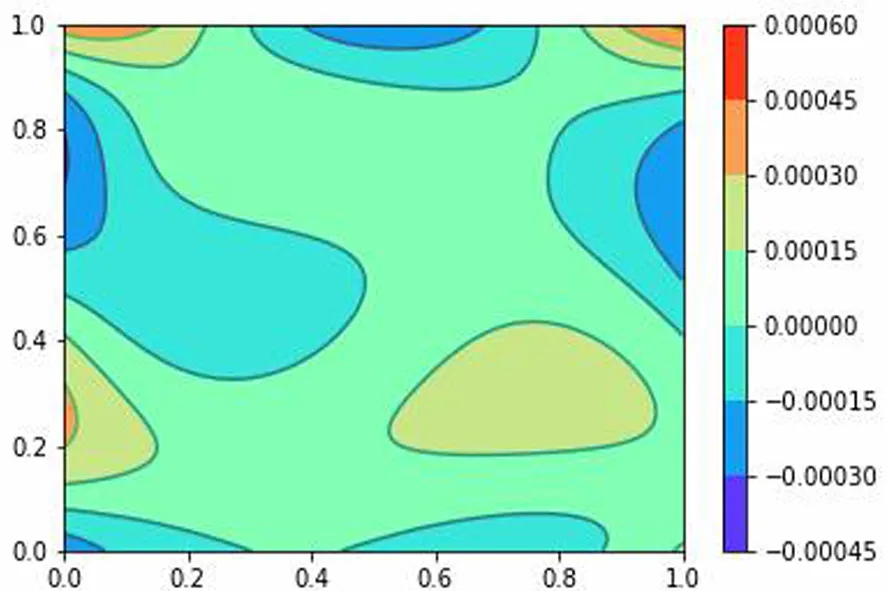
图3 精确解和近似解误差图

由计算结果可以看出，深度神经网络求解Helmholtz方程的误差在10-4左右，计算效果较为理想，下面介绍利用深度神经网络求于参数识别反问题的过程.

3.2 反问题的设置

考虑Helmholtz方程(2)的参数识别反问题.取

f(x,y)=e-x(3x-2+6y+3y3),g1(y)=y3,

g2(y)=(1+y3)e-1,c1(x)=xe-x,c2(x)=(x+1)e-x.

(10)

接下来，我们用如下均方误差的和作为损失函数

(11)

算法3: PINNs解Helmholtz方程反问题算法步骤1: 构建深度神经网络n(x,y,θ)作为真解U(x,y)的近似值;步骤2: 初始化参数θ,p,k2,也就是神经网络的权w和偏差b还有方程未知参数p和k2;步骤3: 选取边界点训练集,方程配置点训练集和测量数据训练集大小;步骤4: 利用自动微分技术求出微分方程残差F(x,y;θ,p,k2);步骤5: 根据边界条件,已知的训练数据和第三步得到的方程残差得到损失函数L(θ,p,k2);步骤6: 利用Adam算法对神经网络参数θ和方程参数p和k2进行训练来最小化损失函数L(θ,p,k2);步骤7: 直到损失损失函数L(θ,p,k2)达到我们想要的精度或者达到最大训练步数停止得到最终的近似解n(x,y,θ*)和反演参数p和k2.

同样地，我们选取一个100×100的网格点，以及U(x,y)在x=1/3处的测量数据作为我们的训练点集.在固定网络和方程的初始参数后同时给定：无噪声、0.5%和1%噪声的测量数据，经过训练后得出损失函数的变化如图4所示，可以看出：测量数据的噪声越大，损失函数收敛的精度也就越低.

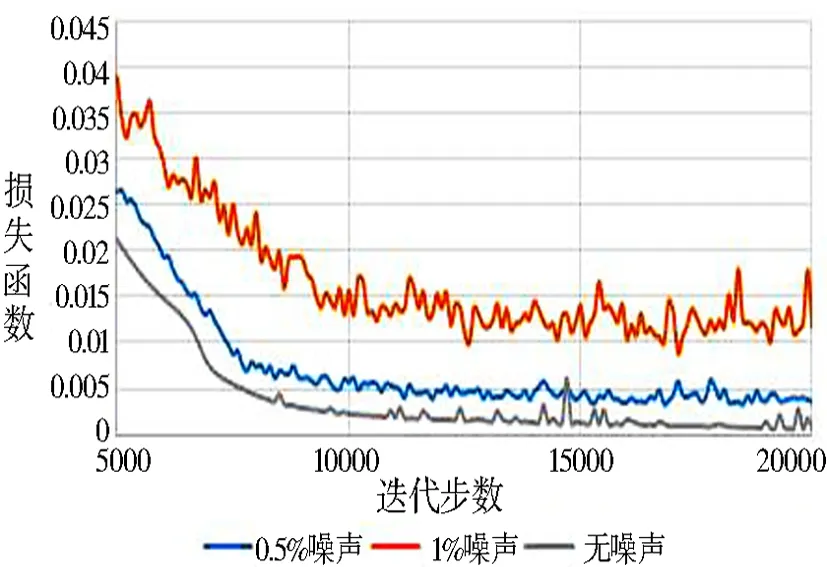
图4 损失函数随迭代步数的变化图

图5 精确解和近似解对比图

图6 精确解和近似解误差对比

随后，我们也得到了训练后的参数p和k2的近似值，下表我们列出了参数p和k2的识别结果和相对误差.

表1 参数p,k2识别结果与相对误差表

4 结论

本文利用PINNs对Helmholtz方程的正、反问题分别进行了求解，该方法利用了深度神经网络逼近定理去逼近精确解U，在给定数据和偏微分方程的约束下，对网络进行训练.数值算例表明，该方法对于求解Helmholtz方程正问题以及参数识别反问题都是有效且具有较好的抗噪稳定性.