基于机器学习BP算法和树模型算法的井筒流体流型预测
*张怡然 李奥
(长江大学地球物理与石油资源学院 湖北 430100)
引言
为了使油气生产更加科学化、高效化,对测井方案的设计是进行生产测井前的关键环节,设计环节中需要选取合适的测井仪器,估算产量,对井下流体进行流型判断等。其中,对井下流体流型的判断是非常重要的步骤,流体流型判断直接关系到后续对整个测井方案的制订以及对测井仪器的选用,避免因为方案不合适导致的浪费。
近年来随着计算机技术的不断进步,人们通过对已有的数据集进行机器学习,能够很好的对新的数据进行预测,国内外已经有运用机器学习神经网络等手段对流体物性参数(PVT)进行处理预测的先例[1],因而利用机器学习方案处理井下数据,进而对井下流体流型进行预测不失为一种可行的方案。同时通过将传统测井与机器学习算法相结合,有助于整个测井行业进入智能化、高效化的新发展阶段,更加符合新时代下传统产业数字化转型,促进新技术在传统行业中发挥作用。
1.算法原理
(1)BP神经网络分类算法
其基本原理如下[2,3]:利用多层感知机(Multilayer Perceptron,MLP),根据现有的大量已知数据,将每条数据的特征汇总成数据集X={x1,x2……xn},每条数据都对应一个标签y,通过对数据集上训练来学习函数f(·):Rn→Ro,其中,n为数据集中数据的维数;o为输出后的维数。和传统线性回归不同,在通过MLP进行学习时,输入层和输出层之间,会存在一个或多个非线性层,称为隐藏层,图1为一个具有两层隐藏层的MLP。
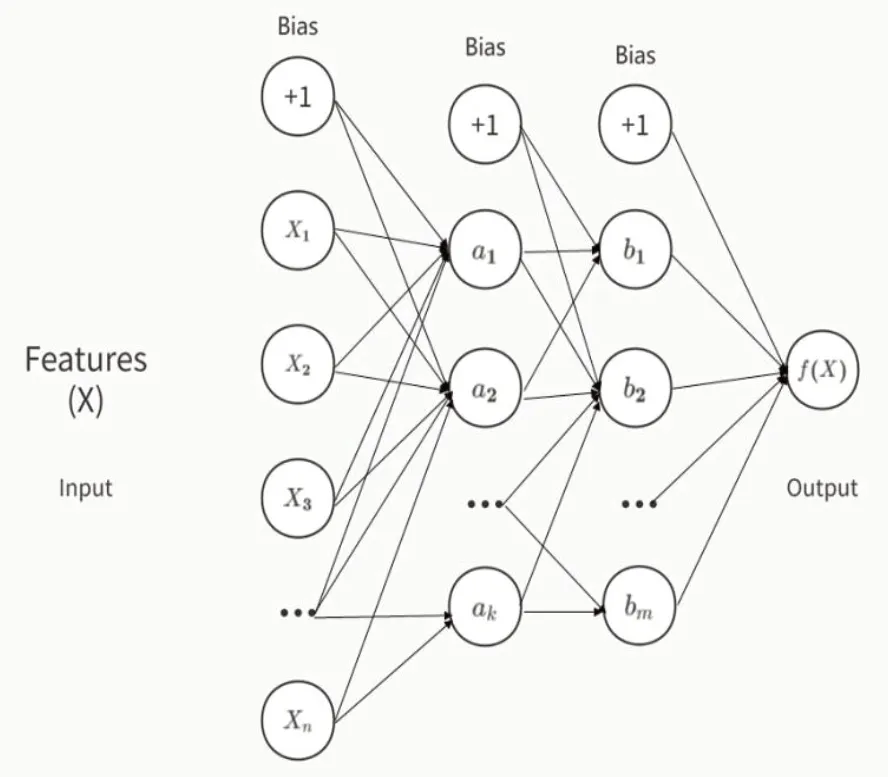
图1 具有两层隐藏层的BP神经网络
最左边的层叫输入层,将已有数据标准化后,作为代表输入特征的神经元;然后经过一层或多层隐藏层中的神经元将前一层的数据加权线性求和转换w1x1+w2x2+……+wnxn,并通过非线性函数g(·)R→R,g(·)也被称为激活函数,通常采用:

最后由输出层接收最后一个隐藏层转换后的值。
MLP采用了随机梯度下降(Stochastic Gradient Descent)进行训练,将需要调整的参数通过使用损失函数进行梯度更新,以获取更新后的参数:

其中,η为控制参数空间搜索步长的学习速率;Loss为神经网络的损失函数。
MLP采用均方差损失函数:
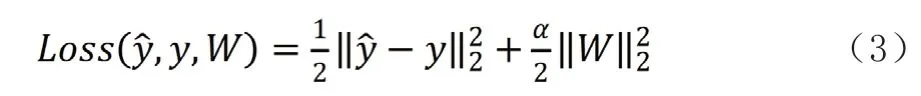
在最初的随机化权重时,多层感知机通过重复更新权重,使得损失的值最小,在计算损失之后,反向传递至输出层的前一层,为每一个权重参数提供一个更新值,从而减少误差。
随着梯度下降,计算得到对每一个权重所损失的梯度▽Lossw,并从总损失中减去,即:

由于在对井下流体流型的预测中,井下流体参数并不是唯一的,因而需要解决多个类同时存在的情况,故在隐藏层中学习函数f(x)=W2g(W1Tx+b1)+b2本身为一个n维向量,通过Softmax函数:

其中,zi为Softmax中输入的第i个元素,其对应与相应的第i类;K是所有类别的总数量,输出的值包含了样本中属于每一个类的概率的向量,最终输出的结果为概率最高的类。
(2)树模型分类算法
其基本原理如下[4]:通过创造一个模型,使程序对该模型进行学习,最终从模型数据特征中推断出的简单决策规则来预测新的输入变量的值。
将已有的数据标准化后分条作为训练向量xi∈Rn,i=1,……,l和类向量y∈Rl,利用决策树递归划分空间,将相同类别的样本划分至同一个组,节点m处的数据集用Q表示,对于一个由特征j和阈值tm组成的阶段划分数据集θ=(j,tm),将数据分别作为两个分支:
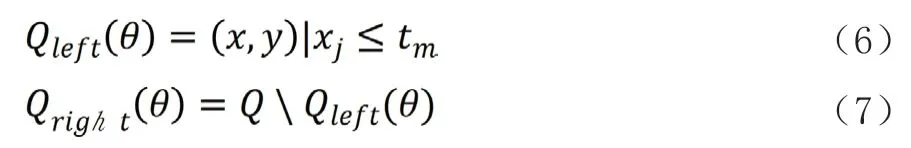
节点处的不存度用不存度函数H(·)计算:
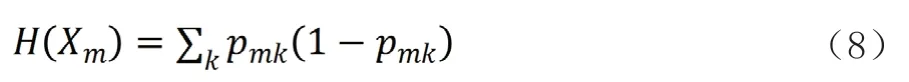
其中,Pmk表示在具有Nm个观测值的区域Rm中,节点m在k类中所占的比例,故Pmk公式为:

Xm为节点m中所包含的已知数据。
井下流体包含多种流体种类,因而得出的结论也是多种类的,故需要将类向量集定义为一个二维的数组;对每一种输出的结果需要建立一个估计器,依据每一种类别的输出平均减少量来作为每一棵分支的产生标准。
2.方法应用
由于实际生产情况具有多种不同井况条件,因而分别采用了在井斜角度0°、60°、85°、90°下,含水率20%、40%、60%、80%、90%,流量100m3/d,300m3/d,600m3/d的实验数据,各个数据间差异较大,如果直接使用会造成部分数据所占权重过大影响最终结果的情况,因而需要对数据进行标准化处理,采用离差标准化处理,使得所有数据结果值映射到[0,1]区间内,所用函数如下:

其中,xmax为数据中的最大值;xmin为数据中最小值。
然后将标准化处理的数据集中每个数据分别进行加权线性求和,利用损失函数计算损失后反向传播至前一层以减小误差,最终达到设定的最大迭代数时结束计算,BP分类算法结束。
再对标准化处理的数据进行评估,选出其中最具有决定性的特征,然后将原始数据集划分为几个子集,这些子集分布在第一个决策点的所有分支上,如果一个分支上所有数据都是同一类别,则不需要继续分类,若包含有不同类别,则需要继续选出最具有决定性特征来继续划分,直至所有叶子节点上的类同属于一类特征,图2为决策树模型运算结果,决策树算法结束[5]。
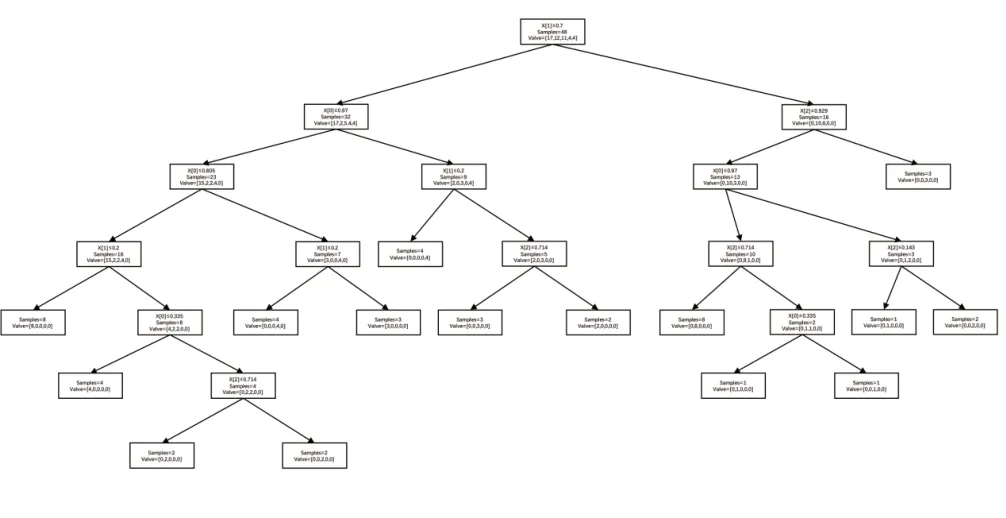
图2 良好决策节点进行决策分支的决策树
3.实验
(1)设计实验
实验所用的数据包括实验数据和实际数据,将实验数据作为数据集以供机器学习算法学习,然后将实际数据输入学习后的算法进行预测,将预测后的结果和实际流体流型进行对比,以检验算法的可行性。
实验数据包含井斜角度、流体流量(m3/d)、含水率、温度、管径,将实际数据带入至通过实验数据训练学习后的模型,得到对实际数据预测的流体流型,与实际结果进行对照;通过分析不同流量、井斜、含水率下的准确度,判断算法的可行性。
(2)预测结果分析
在学习算法结束之后,随机选取不同井斜、含水率、流量的12组已知数据,对数据进行预处理后,然后使用训练过的神经网络进行预测,将预测结果与实际数据进行对比,以检验BP分类算法和树模型分类算法对流型预测的准确率。
BP分类算法和树模型预测结果如表1所示。

表1 BP分类算法与树模型预测结果
从表1可知,在井斜角度较低时,BP分类算法得到的预测结果较井斜角度较大时的准确度有大幅度提升,在井斜角度较大时预测准确率较低,总的预测准确度在75%左右。而从图3来看,决策树模型在决策点选择较好的情况下,在各流量、各井斜、各含水率上均有较为准确的预测结果,总体准确度能达到90%以上。

图3 两种算法与实际流型结果比较
4.结论
将实验数据分别按照BP分类算法和树模型算法进行预测后与实际流体流型对比后可以得到如下结论:
(1)通过机器学习BP分类算法和树模型算法进行井筒流体流型预测,对井下流体流型预测提供了新的解决方案。其中BP分类算法在井斜角度较大的情况下能取得95%以上的准确识别率,但是在其他条件下效果较差;树模型算法在各种井斜、流量、含水率下均有较为准确的预测,综合准确度在91.7%左右。
(2)通过较为合适的数据标准化处理,可以降低某些数据在预测中占有过高权重,减少了数据处理后的误差,提高了数据处理的效率。
(3)通过不断完善训练数据集的数据,可以不断提升预测结果的准确度,为后续该算法在实际应用中打下良好基础。

