基于非线性方程组的非单调信赖域算法研究*

唐江花

(安徽新华学院通识教育部,安徽 合肥 230088)

引言

随着金融、贸易、计算机等方面的发展，越来越多的非线性规划问题开始出现[1].针对这些最优化问题进行求解，成为数值求解方法的重要研究方向.信赖域算法的设计是以线性规划为基础，其核心在于探索试探步长，通过多次计算求解每个信赖域子问题，获取初始试探步长，再分析函数下降量趋势，判断试探步长的合理性[2].非单调信赖域方法因具有较强的收敛性，受到很多研究人员的关注，多种类型的信赖域方法开始得以应用.

文献[3]针对不等式约束优化问题进行研究，引入指数型增广Lagrange函数计算理念，将最初的优化求解问题，转换为信赖域子问题，形成一个可以应用于问题求解的信赖域算法.但是，该算法计算复杂度较高.文献[4]以加强最优化求解准确度为目标，提出融合了多维滤子算法的信赖域算法.分别计算目标函数分量，以及函数投影梯度的分量信息，提取可以判断信赖域半径合理性的过滤点.同时，需要验证提取出的多维滤子可以接受试探点，确保整体收敛性达到要求.但是，该算法的计算时间较长.文献[5]设计了一种一类序列、二次规划同时存在的信赖域算法，且该算法具有不相容性特点.参考传统算法设置参数变量，并更新目标函数相关的参数.应用多维滤子算法，选择最优迭代步作为试探步长.最后，利用二阶校正策略，校正算法运行过程中存在的maratos效应.但是，该算法运算迭代次数较多.

为了解决上述提出非单调信赖域算法的缺点，文中设计的算法以非线性方程组为基础.将具有非线性规划特点的规划问题，转化为非线性方程组.通过非线性约束环境下，最大或最小值的提取，搜索到最优目标函数值.同时，运用Hessian矩阵和双割线折线算法，对现有的试探步长求解过程进行简化，保证算法求解结果准确性的同时，减少迭代次数.

1 基于非线性方程组的非单调信赖域算法设计

1.1 非线性方程组问题转换

约束优化问题的求解关键环节之一，就是非线性方程组的求解.文中提出的非单调信赖域算法，将非线性方程组问题转换的研究[6]，作为核心研究问题.依托于非单调技术和信赖域计算理念，完成非线性方程组，与非线性优化之间的互相转换，降低后续信赖域算法的运算复杂度.

将最初非线性方程组表示为：

F(x)=0,
x∈R

(1)

公式中，x表示变量，F(x)表示函数，R表示连续可微的实值函数.其中：

F(x)=(f1(x),f2(x),…,fm(x))

(2)

公式中，f(x)表示子函数，m表示非线性方程组中包含的子函数数量.再结合向量空间范数，可以将原始方程组表示为：

(3)

公式中，min表示最小值，e表示向量空间，‖·‖e表示向量空间范数.

当向量空间取值为2时，可以将非线性方程组求解问题，看作最小二乘问题，选取最优方法进行后续求解.但是，当向量空间取值范围为正无穷状态时，可以将最初的问题看作求解优化问题[7].这种情况下，函数具有不可微特性，造成数值计算难度较大.针对该问题，文中提出在非线性方程组问题转换过程中，融入极大熵函数，有效控制参数值.文中所应用的极大熵函数为凝聚函数，根据原始函数的指数函数，并获取范数的自然对数.其中，指数计算过程中，需要保证向量为正分量，对数的计算，是为了保证函数值恢复成最初模样.

考虑到向量空间取值无穷大条件下，非线性方程组的函数空间拟合值与参数值之间具有反比例关系.因此，非单调信赖域运算过程中，需要确保向量空间取值够大，并应用可微函数替换方程组中部分参数，将非线性方程组转换为易于求解的无约束优化问题，作为最优化求解的基础.

1.2 设计非单调信赖域模型

非单调信赖域算法设计过程中，融合Hessian矩阵，实现试探步长计算复杂度降低.信赖域方法的运行，对于Hessian矩阵在每个迭代点的正定与否，没有强制要求.对于不合理的试探步长，可以采用二阶校正的方式进行更新，得到优化后的试探步长.同时，以将信赖域内第一个迭代点为核心[8]，形成一个闭球邻域.再添加一个自然数，判断信赖域半径是否成功.

实际操作过程中，信赖域子问题的求解是计算初始试探步长的基础，文中将信赖域算法数学模型表示为：

(4)

公式中，w表示二次模型，P表示目标函数，jP表示迭代点上对目标函数的恰当模拟，j表示目标函数梯度，ϖ表示Hessian阵.式中：

(5)

运用公式(5)所示的Hessian阵，以近似序列的形式将目标函数与导数函数信息表现出来.

依托于非线性方程组进行子问题求解，需要对目标函数曲率进行修正[9]，得到最优解.根据近似序列构建近似矩阵，完成矩阵正定处理后，提取出最优曲线，从初始点延伸出一条平行于牛顿方向的切线，形成双割线，如图1所示.运用双割线法快速计算出信赖域子问题的最优解.

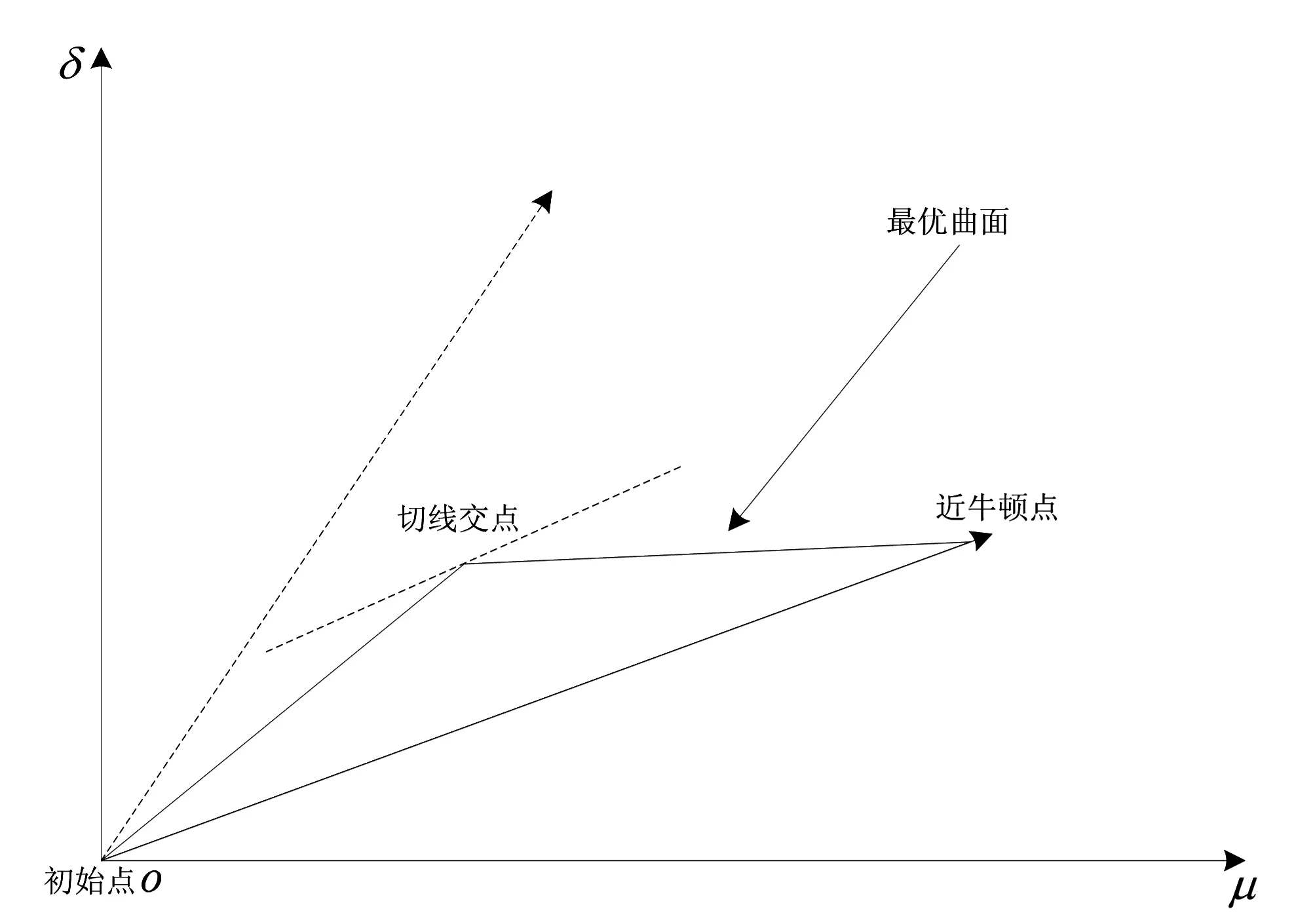
图1 双割线折线图示

根据图1所示的双割线折线算法，对子问题求解模式进行改进，其核心思想是运用低阶欧拉方法求解出以最优曲线为基础构建的微分方程模型[10].通过正常、平均和隐式欧拉折线，取代最优曲线求解子问题的模式，保证近似矩阵正定的基础上，克服详细数值的奇异性，简单而快速地完成信赖域子问题的求解，得到试探步长.

1.3 建立多维过滤集

根据融合Hessian矩阵和双割线折线算法的非单调信赖域模型，求解出试探步长，作为最优解计算的基础.为了保证简化计算结果不会影响最优化求解的准确性，文中依托于包含插值自由度信息的锥模型建立多维过滤集，进一步判断试探步长的可行性.针对当前迭代点设计一个试探步长，可将二者的关系表示为：

ak+1=ak+φ

(6)

公式中，k表示迭代次数，a表示迭代点，φ表示试探步长.为了便于非线性方程组求解效率的提升，将信赖域子问题表示为：

(7)

公式中，β表示信赖域子问题，v表示水平向量，B表示子函数在迭代点的Hesse近似，也称为实对称矩阵.

由于水平向量条件并非一项苛刻要求，正常情况下该条件可以被满足，可以直接运用计算出的试探步长，求解非线性方程组，对比方程组求解结果与理论分析值，判断上述计算出的试探步长的有效性.另外一种情况，就是信赖域子问题求解过程中，水平向量条件没有得到满足，无法直接判定试探步长.为此，文中提出将信赖域子问题求解结果划分为三种状态，针对不同的情形，设置相对应的最优性条件.综上所述，将子问题处理模式设置为：

(8)

(9)

公式中，α、δ表示两个变量，λ表示试探点，g表示过滤点.

针对试探点进行迭代更新后，结合信赖域子问题求解结果，建立多维过滤集，判断求解出的试探步长是否合理.针对满足要求的试探点，运用“占优”准则，选取出最优过滤点，生成多维过滤集：

U=(gk,1,gk,2,gk,3,…,gk,N)

(10)

公式中，U表示多维过滤集，N表示过滤点分量.当某一个试探点不存在迭代点占优情况，可以直接将该点添加到过滤集中.反之，则需要采用封套策略，分析函数下降量趋势,进行过滤点选取，封套策略的具体表达公式为：

|gk,n|≤|gk+1,n|-ϑ‖gk+1‖

(11)

公式中，ϑ表示封套系数.将满足公式(11)的试探点，添加到过滤集中，反之则将其挡在过滤集之外.最后，采用Nowton校正策略对实对称矩阵进行校正，Nowton校正模型如图2所示.

运用图2所示的Nowton校正模型，对实对称矩阵进行校正，将子函数在迭代点的Hesse近似值替换为实际值.通过上述计算完成多维过滤集的整体建立，运用过滤集对初步求解出的试探步长进行处理，采用符合要求的试探步长进行非线性方程组的求解.

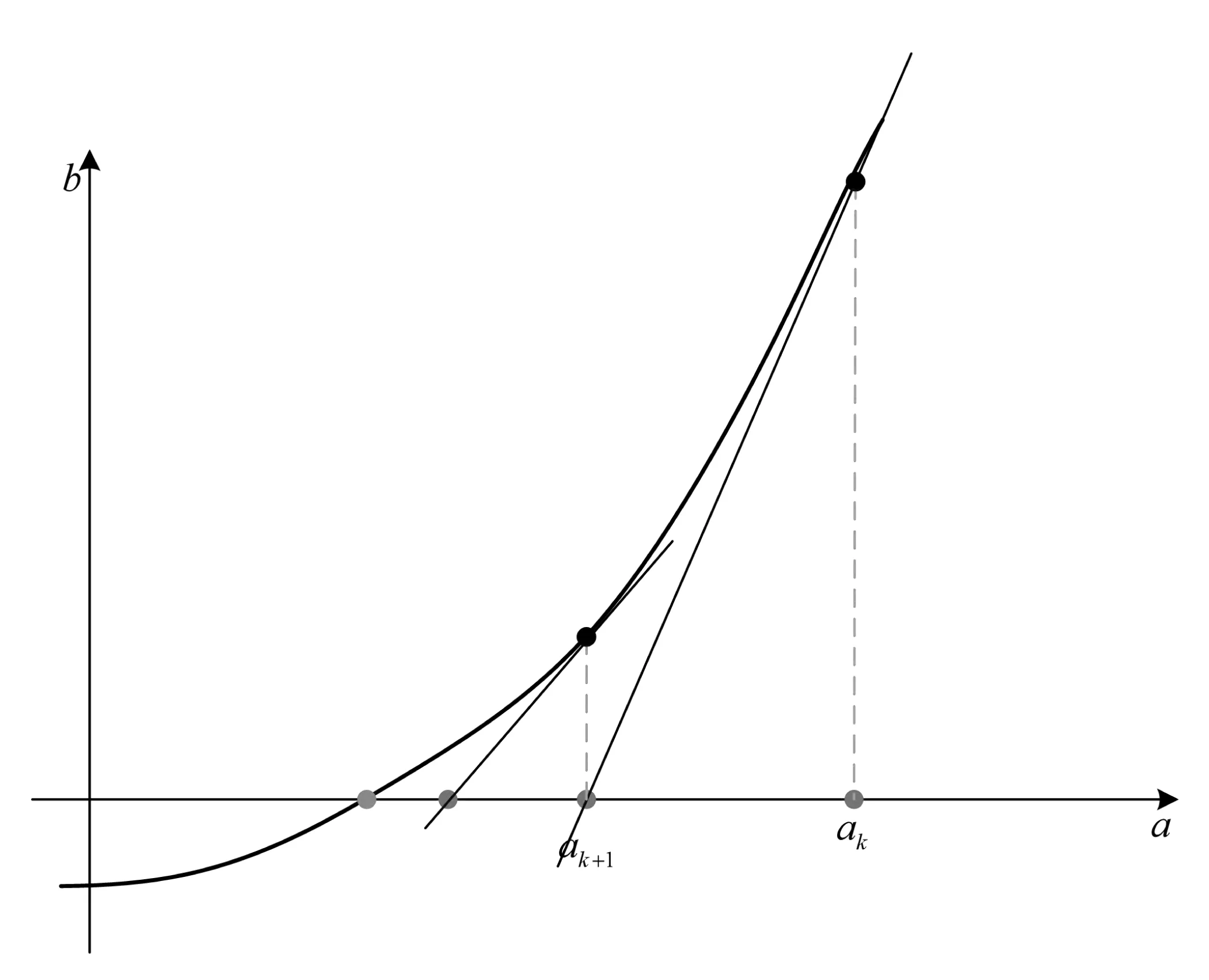
图2 Nowton校正模型

1.4 完成信赖域算法设计

非单调信赖域算法研究的最后一步，就是验证所提出算法的全局收敛性，文中考虑无约束优化特点，假设非线性方程组具有连续可微特点，则以此为基础建立的Jacobian矩阵同样具有连续性，可得到：

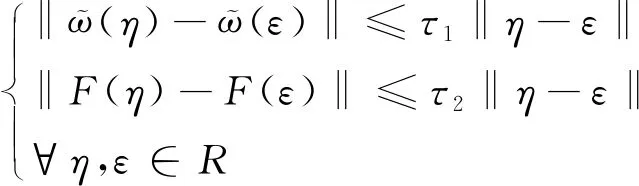
(12)

公式中，η表示因变量，ε表示自变量，τ1、τ2表示正常数.根据公式(12)可以得出：

‖F(ε)‖=‖F(η+r)‖≤‖F+r‖+τ1‖r‖2
≤‖F‖+τ2‖r‖+τ1‖r‖2

(13)

公式中，r表示连续收敛系数.通过上述计算，得到具有连续性的迭代序列，生成如下所示收敛函数：

‖F(ε)-F(η)-ϖ(ε)(η-ε)‖≤τ1‖η-ε‖

(14)

根据非线性方程组的变量信息，应用反证法验证非单调信赖域算法的全局收敛性.考虑到算法运行时存在两种状态，其一是有限迭代次数情况，其二是无限迭代次数情况.前者可以根据计算结果进行直接判断，文中主要针对后者进行分析，结合迭代次数值的属性特点，提出极限条件下第一阶段和第二阶段函数收敛性验证结果为：

(15)

公式中，part1表示第一阶段，part2表示第二阶段，lim表示极限符号，∞表示正无穷.

根据公式(15)可知，第一阶段和第二阶段全局收敛已经达到0，而信赖域算法的收敛性验证结果主要取决于第三阶段收敛验证结果.当第三阶段收敛为0，表明该算法的全局收敛性最强，同样，计算结果越接近1，表明算法收敛性能越差.考虑到正常运算过程中有一个正常数作为判断阈值，全局收敛性验证结果超过判断阈值，表明该算法不成立，需要重新调整参数信息.当验证结果低于判断阈值，表明文中设计算法的全局收敛性达到要求，可以作用于最优化问题求解中.

2 数值实验

2.1 实验函数

依托于非线性方程组，完成非单调信赖域算法设计后.为了研究该算法的可行性和有效性，文中运用MATLAB仿真软件进行数值实验，针对同一组实验函数，分别运用文中设计算法，和传统信赖域算法进行数值分析，对比不同算法计算出的数值结果，判断文中设计算法的优越性.为了加强实验结果的说服力，设置数值实验在同一台计算机上进行，并在MATLAB 6.5环境下运行非单调信赖域算法.本次实验所应用的实验函数为：

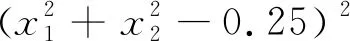
(16)

为了便于运算，数值实验展开之前对实验函数深入分析，并绘制该函数的三维空间图像，得到图3所示的函数图像.

图3 函数三维图像

根据图3可以看出，本次所应用的实验函数为典型函数，以该函数为基础，进行非单调信赖域运算1，并记录数值运算结果.

2.2 运算结果

运用文中设计算法对实验函数进行数次迭代计算，从不同初始点开始进行运算，将实验函数转化为非线性方程组问题再进行迭代计算，记录算法运行后，生成最优目标函数值所需的迭代次数，以及相应的最优目标函数值，形成表1所示的数值计算统计表.

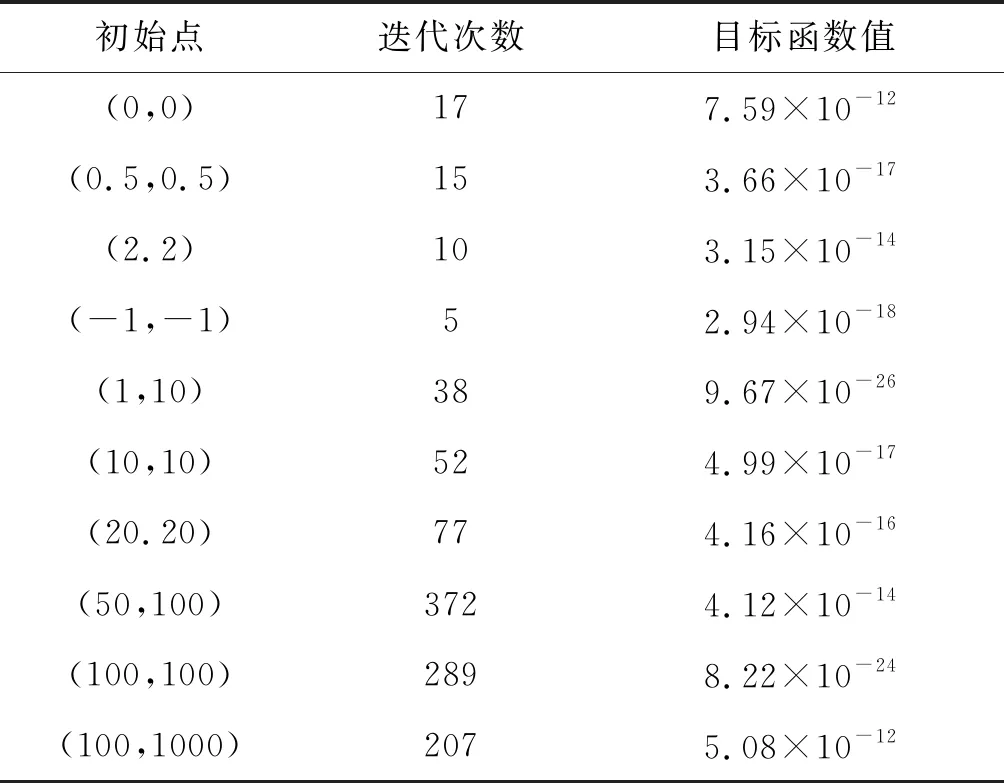
表1 数值计算结果

根据表1可知，运用文中提出的非单调信赖域算法进行数值分析，在不同初始点条件下，经过数次迭代，分别求解出了实验函数的最优目标函数值，表明所提算法具有可行性.

2.3 算法性能分析

为了加强算法性能分析结果的直观性，运用ANIR算法和MNMTRLS算法，在同样的实验环境下，进行数值分析，对不同算法的迭代性能进行分析.为了更好地评估算法的总体性能，分析性能比率的累积分布函数：

(17)

公式中，t表示问题，φ表示测试问题的集合，u表示算法的性能比，ξ表示最佳可能比率因子，γ表示测试问题数量，σ表示非单调信赖域算法，T表示性能比率的累积分布函数.基于公式(17)，结合不同算法的运行结果，得出图4所示的迭代次数对比图.

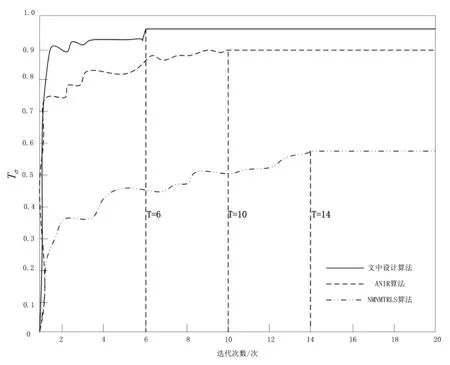
图4 不同算法的迭代次数对比图

根据图4可知，文中提出的非单调信赖域算法实际运行后，与ANIR算法和MNMTRLS算法相比，具有更好的迭代次数性能.通过计算可知，以非线性方程组为基础的算法，大大简化了试探步长计算步骤，使得该算法的迭代次数减少了40%～57%，在实际优化问题上竞争力更强.

3 结束语

为了更好地求解出无约束优化问题，信赖域方法得到广泛应用，本文以解决信赖域算法运算复杂度较高的缺点为目标，提出了以非线性方程组为基础的算法.将所有问题转换为非线性方程组，再结合Hessian矩阵和双割线折线算法，简化了信赖域试探步长计算步骤，形成一种迭代性能更佳的非单调信赖域算法.

经过实验可知，文中设计算法的应用效果达到了预期目标.但是，随着最优化要求的不断提升，还需要进一步完善非单调信赖域算法.一方面需要分析信赖域子问题类型，建立相应的数学模型.另一方面则是依托于智能时代的发展，运用机器学习技术求解大规模无约束优化问题，对非单调信赖域算法进行改进.