静压造型线伺服直驱泵控液压系统设计*
王琳琳
(安徽冶金科技职业学院机械系,安徽 马鞍山 243000)
引言
交流电机调速技术的迅猛发展,使伺服直驱泵控液压系统的设计技术日趋成熟,该系统是融合伺服电机控制和容积控制两种技术的新型传动系统[1],可以通过对伺服电机的调速、换向等功能,直接驱动定量泵进行方向和速度的切换,控制执行元件的压力以及位置等,同时该系统具有集成度高、易于控制和高效节能等优势[2].静压造型线作为一种自动铸造设备,因具有成型效果好与自动化水平高等特点,已逐渐成为各铸造厂的核心设备之一.近年来伺服直驱泵控液压系统在静压造型线中获得广泛应用,系统的控制效果对保证静压造型线安全稳定运行起着重要作用,但由于系统控制的动态响应较慢[3-4],导致伺服直驱泵控液压系统对静压造型线的控制效果不理想,因此设计性能较好的静压造型线伺服直驱泵控液压系统具有重要意义.
当前针对此类系统的设计成果有很多,例如魏秋红等人[5]和杨可可等人[6],分别使用分数阶控制器以及鲁棒H∞控制,实现静压造型线伺服直驱泵控液压系统设计.虽然以上两种系统的动态特性明显改善,且能量消耗较少,但对负载干扰和参数摄动的抑制能力较差.为解决以上研究存在的问题,本文以小波神经网络控制器为核心设计静压造型线伺服直驱泵控液压系统,以进一步提升系统的控制性能,为静压造型线的顺利运行提供更好的保障.
1 静压造型线伺服直驱泵控液压系统
1.1 静压造型线伺服直驱泵控液压系统结构
静压造型线伺服直驱泵控液压系统包含计算机控制部分、伺服调速部分以及液压动力机构,系统具体结构如图1所示.
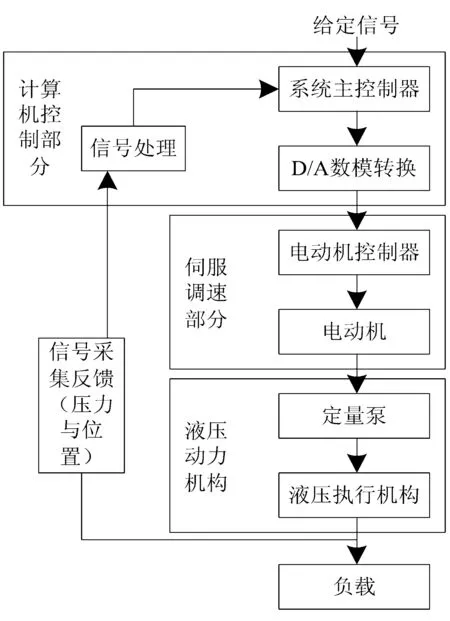
图1 静压造型线伺服直驱泵控液压系统结构
信号采集反馈模块使用压缩感知方法获取静压造型线内液压缸的压力和位置信号,将其传输到计算机控制部分的主控制器进行比较处理,运用D/A数模转换模块转化信号处理结果,使其变为控制信号,并传送到伺服调速部分的电动机控制器[7],其控制电动机直接驱动定量泵执行方向和速度的切换,以达到控制静压造型线内液压缸的目的.该系统属于闭环控制系统,可以依据返回的信号值实时调整伺服电机,以满足负载变化的需求.
1.2 基于压缩感知的信号采集方法
假设长度有限且维数为n的信号用x表示,若想表明x在某个矩阵ψ上具有稀疏性,则该矩阵应满足公式(1)所示表达式:
x=ψz,‖z‖0=k
(1)
式(1)中,原始信号用x表示;稀疏向量用z表示,且满足x,z∈Rn×1;稀疏矩阵用ψ表示,且满足ψ∈Rn×n;稀疏度用k表示;向量z的l0范数用‖z‖0表示.
假设测量矩阵用φ表示,在该矩阵内满足条件y=φx的情况下,通过公式(2)所示关于l0范数的最优化问题的求解,可以实现x的高概率重构,重构方式以及重构误差的计算过程如公式(3)、(4)所示:
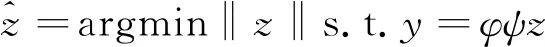
(2)
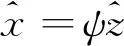
(3)
(4)
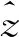
依据上述压缩感知理论可得,用x代表静压造型线内液压缸的压力和位置原始信号,且φ为随机矩阵的情况下,可认为y=φx表示对压力与位置信号进行随机采样[8-9].因为测量向量维数m的值比信号维数n的值小,所以在静压造型线内液压缸的压力和位置信号采集过程中还实现了信号数据压缩[10],对降低信号采样频率以及提高后续信号转换效果具有重要作用.下述为所选用加性随机采样方法的具体过程.
步骤一:依据静压造型线内液压缸的压力和位置信号特点、矩阵维数以及信号重构精度等因素,运用下式对采样时间窗进行计算:
Tw=n/fs
(5)
式(5)中,采样时间窗用Tw表示,单位为s;采样频率用fs表示,单位为Hz.每个采样时刻值的计算过程如公式(6)所示:
ti=ti-1+τi
(6)
式(6)中,次序为i的采样时刻用ti表示,其中i的取值介于[1,α]范围内,采样时刻间隔用τi表示.
步骤二:当τi属于高斯随机数时,通过上式获得采样时刻序列,因此可得到公式(7)所示结果:
τi=(Aa,Bb)+s×N(0,1)
(7)
式(7)中,收敛因子用(Aa,Bb)表示;时间变动因子用s表示;高斯随机变量用N(0,1)表示.
1.3 小波神经网络控制器设计
由于负载扰动、流量脉动以及电气参数等对静压造型线伺服直驱泵控液压系统的性能具有较大影响[11-13],因此可以利用精准识别异常信号的小波神经网络,实现伺服直驱泵控液压系统对静压造型线内液压缸的压力与位置的双闭环控制.
小波神经网络控制器的网络结构包含输入层、隐含层和输出层.通过归一化处理输入信号样本[14,15],将处理结果传输到隐含层,该层利用选取的小波函数处理接收到的信号样本,并传送到输出层,比较真实输出结果和期望值,运用两者的差值反向训练小波神经网络每个层级的连接权值,重复以上过程,停止条件为网络的全局平方和满足提前预设的精度.
1.3.1 小波神经网络结构及其算法
假设函数空间用L2(R)表示,根据离散小波变换原则,如果给定函数满足ψ(t)∈L2(R),且符合公式(8)所示约束条件,则称ψ(t)为基小波函数.
(8)
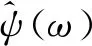
(9)
式(9)中,尺度因子用a表示,平移因子用b表示,a和b满足a,b∈R,且a的值不等于0.
依据以上理论可获得如图2所示的小波神经网络结构.
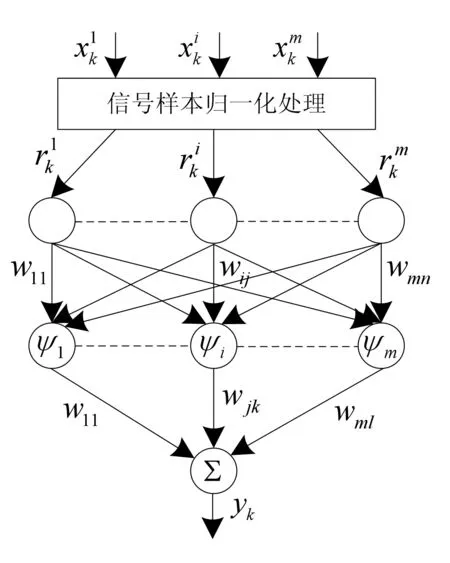
图2 小波神经网络结构图

(10)
式(10)中,隐含层小波函数用ψj(x)表示.
1.3.2 小波神经网络控制器设计过程
步骤一:归一化信号样本.将采集的静压造型线内液压缸的压力和位置信号作为网络的输入信号样本,由于不同信号样本的取值范围具有较大差异,需要使用下式归一化处理信号样本,以避免网络训练过程中陷入局部极值.
(11)
式(11)中,信号样本最大值用xmax表示,最小值用xmin表示.
步骤二:初始化小波神经网络.以随机形式对aj、bj以及网络连接权值ω进行初始化,并将学习速率设定为0.1,动量因子设定为0.06.
步骤三:控制输出.将输入信号样本划分为训练和测试样本两部分,将训练样本作为网络输入,在获得网络控制输出的基础上,对其与期望输出之间的误差E进行计算.
步骤四:权值更新.将E作为依据更新小波函数参数和网络权值,使控制输出结果不断接近期望结果.
2 结果分析
以某铸造厂的静压造型线作为实验对象,在AMESIM仿真环境下,依据本文设计的伺服直驱泵控液压系统,搭建完整的系统模型,该模型的公式为:
(12)
通过该模型对静压造型线内液压缸的压力和位置信号进行采集,并实现相应的控制功能,同时增加负载力干扰,将仿真时间设置成12 s.
使用本文系统采集的静压造型线内液压缸的压力和位置信号,如图3所示.
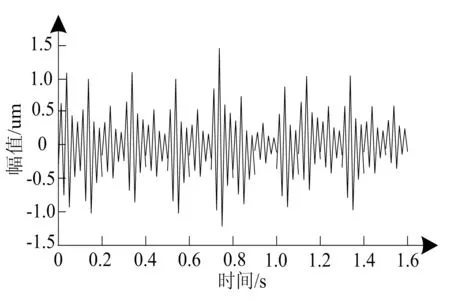
(a)液压缸压力信号波形图
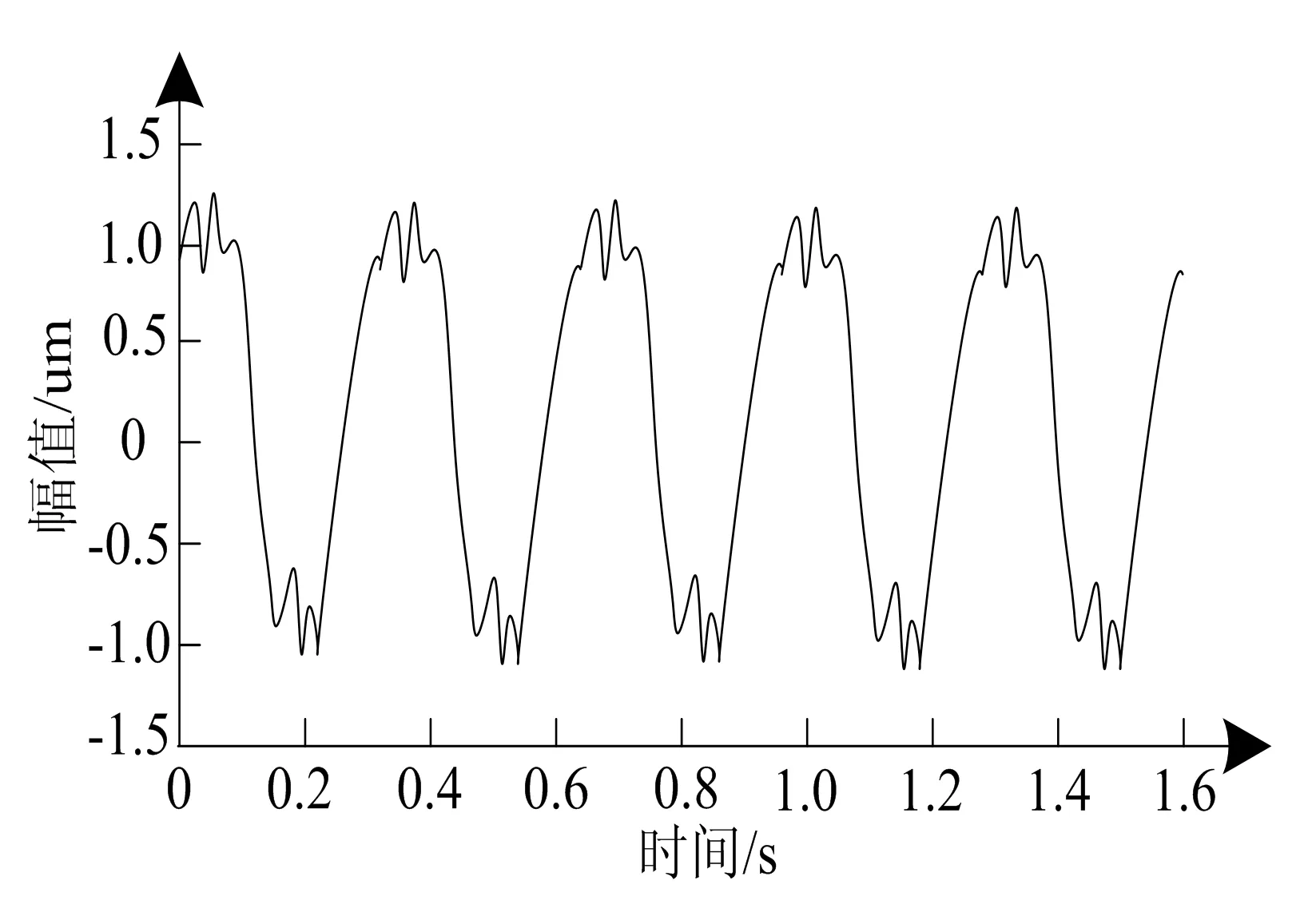
(b)液压缸位置信号波形图
分析图3可以看出,本文系统具有良好的静压造型线内液压缸的压力和位置信号采集效果,所得信号波形完整连续,且不存在噪声,能有效反映不同类型信号特点,有助于提升后续伺服直驱泵控液压系统对静压造型线的控制精度.
当伺服直驱泵控液压系统存在不同程度的负载力干扰时,获得的静压造型线内液压缸A和液压缸B的位移跟踪响应结果,如图4所示.

图4 不同液压缸的位移跟踪响应结果
分析图4可以发现,当伺服直驱泵控液压系统的负载力干扰小于2 000 N时,静压造型线内液压缸A和液压缸B的实际位移和期望位移基本一致;当负载力干扰大于2 000 N时,两个液压缸的实际位移开始偏离期望位移,但两者之间的差值很小.
因此表明,本文系统能很好地控制静压造型线内液压缸的位置,并且在系统具有较大负载力干扰的情况下,仍能表现出较理想的控制性能.究其原因是本文系统设计的包含输入层、隐含层和输出层的小波神经网络控制器网络结构,可以精准识别异常信号的小波神经网络,实现伺服直驱泵控液压系统对静压造型线内液压缸的压力与位置的双闭环控制,一定程度上有利于提高控制能力.
本文系统使用后,获得的静压造型线内液压缸两个端口的压力响应曲线,如图5所示.
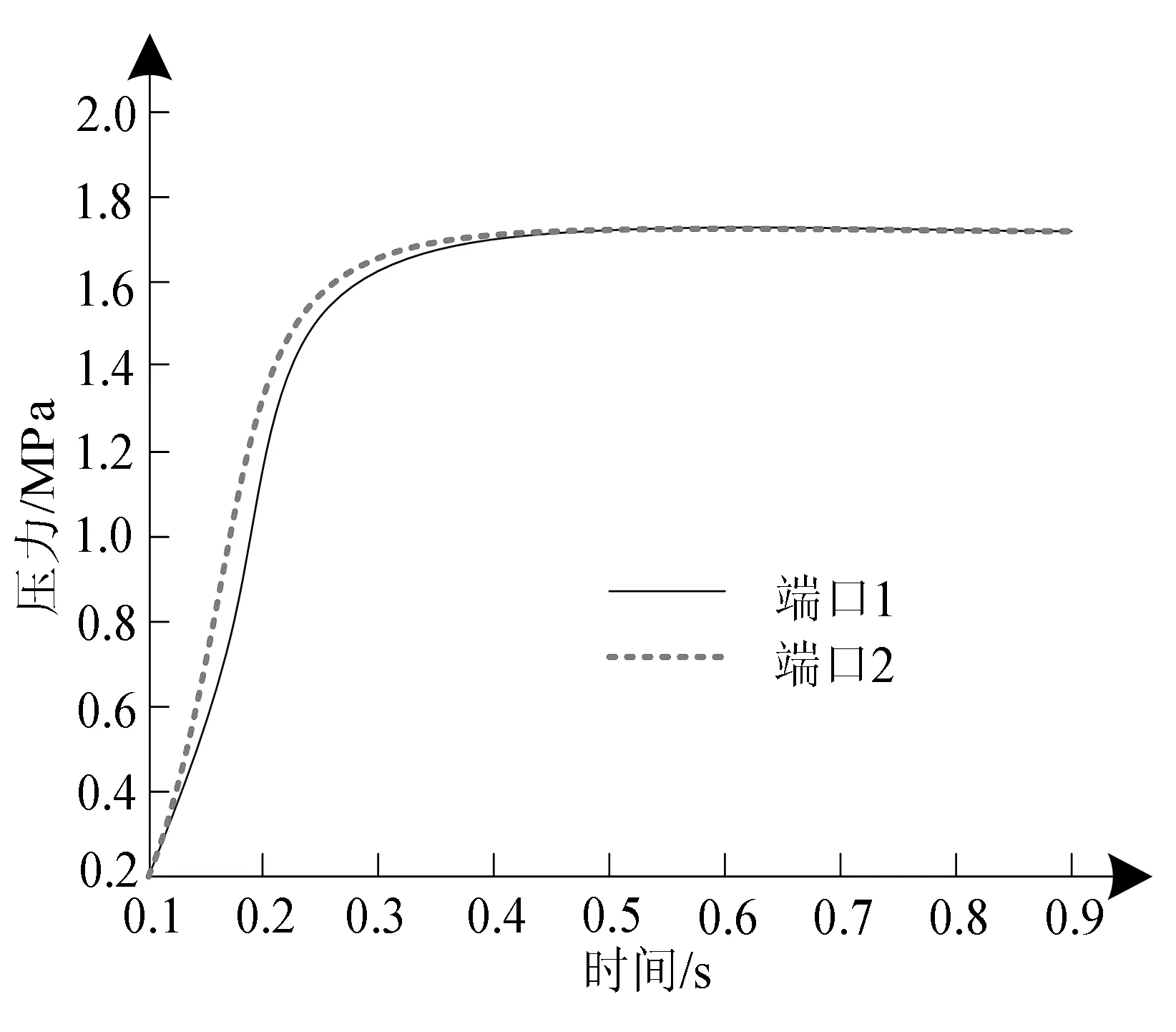
图5 内液压缸两个端口的压力响应曲线
分析图5可以发现,使用本文系统对静压造型线内液压缸的压力进行控制后,液压缸两个端口的压力响应均在0.4 s达到稳定状态,在达到稳态之前,端口2的压力响应速度更快.因此可得,本文系统具有较理想的静压造型线内液压缸的压力控制效果,可以使液压缸不同端口的压力迅速稳定下来,响应快速性较为优良.
静压造型线的运行过程,主要包括工作行程、保压阶段、快速回程以及待机阶段四种状态,测试不同伺服电机转速下,静压造型线处于不同状态时的平均功率,结果如表1所示.
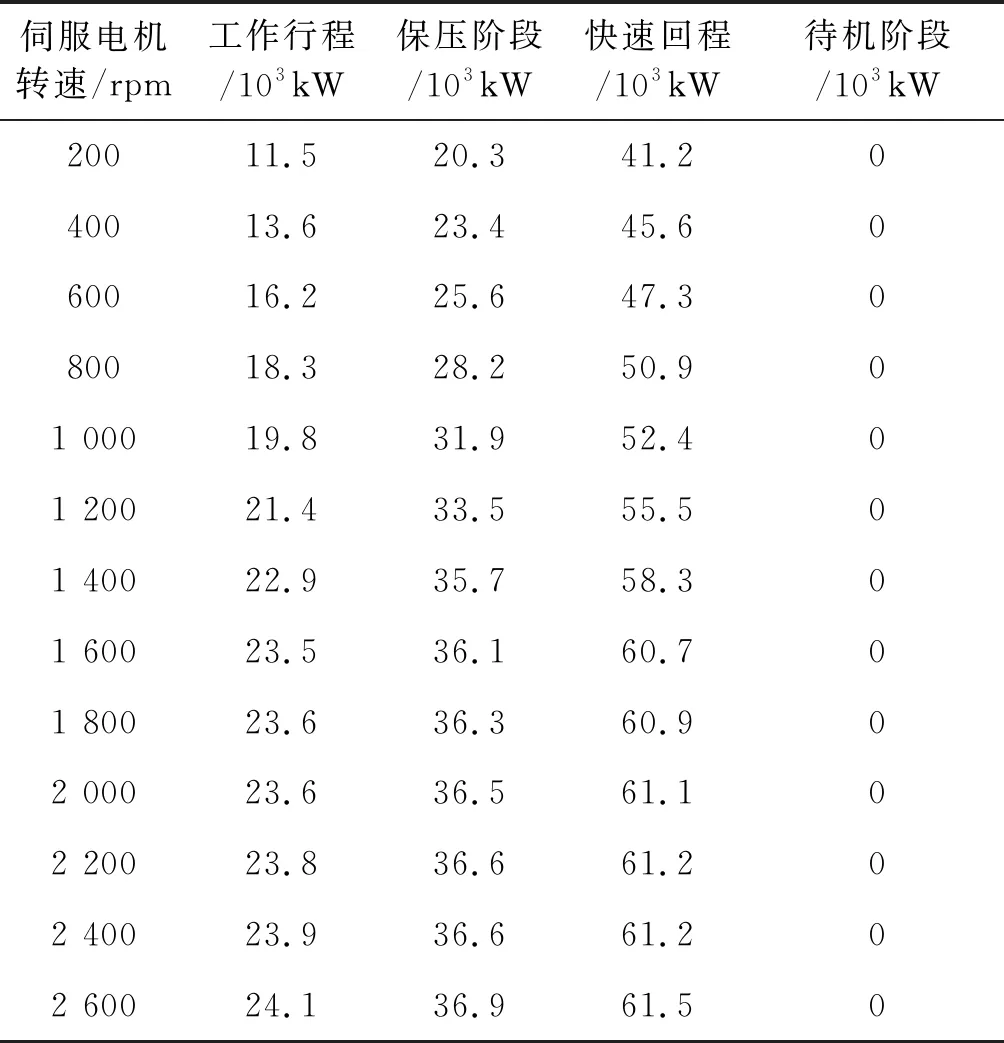
表1 静压造型线不同状态时的平均功率
分析表1可以得出,随着伺服电机转速持续增加,静压造型线处于不同状态时的平均功率均呈现出先缓慢上升,并在伺服电机转速达到1 600 rmp时开始趋于稳定的态势;当静压造型线处于快速回程状态时,不同伺服电机转速下的平均功率始终保持最高,最大值为61.5×103kW;当静压造型线处于待机状态时,伺服电机停止转动,平均功率为0.以上结果可得,伺服电机转速对静压造型线运行过程中的能量消耗具有一定影响,但在伺服电机转速达到某个数值时,不会再过度消耗能量,表明本文系统通过控制可有效保证静压造型线的节能效果.
3 结论
伺服直驱泵控液压系统的控制效果直接关系着静压造型线的安全稳定运行,因此本文设计的静压造型线伺服直驱泵控液压系统,通过对静压造型线内液压缸的压力和位置控制,保证静压造型线能够顺利完成铸造任务.经过仿真分析可知,该系统可以采集到质量较高的液压缸压力和位置信号,且利用小波神经网络控制器能很好地控制液压缸的压力和位置,同时该系统能有效保证静压造型线的节能效果,对促进铸造厂的自动化发展具有重要参考价值.

