高应力下不同节理倾角的隧道稳定性影响研究

杨明明

(中铁十八局集团第一工程有限公司,河北 保定 072750)

0 引言

随着我国西部大开发的快速推进,公路工程、水利水电工程等基础设施大量建设。西部地区地形地势复杂,基础工程建设最大的难题之一就是岩体结构复杂。在漫长的地质活动中,岩体内部存在大量的节理、裂隙及断层等不连续结构面。在极大的原岩应力作用下,在结构面及应力卸载的共同作用下,必然会破坏岩体原有的稳定性,使岩体处于极不稳定状态。因而有必要针对山区深埋岩体,探究在不同节理倾角下隧道开挖对岩体稳定性的影响。

对于节理岩体研究方法,目前主要有经验分析法[1-2]、理论分析[3-4]、室内试验[5-6]及数值模拟[7]等,李剑光等[8]通过颗粒离散元研究了单节理不同倾角对隧道稳定性影响,揭示了节理与洞壁相交处位移较大机制。谷拴成等[9]通过有限元软件及理论推导,得出隧道各层破坏面与垂向夹角,进而推算出冒落拱的高度。杨仁树等[10]通过理论推导获得底板损伤破坏深度及损伤区分布特征,并通过数值计算得出底板的实际应力状态。

从上述以往学者研究不难发现,目前复杂地质工况理论推导存在局限性。随着计算机的发展,数值模拟对复杂工况计算有很大优势,针对岩体的数值模拟,有限元及有限差分等数值软件能够很好地揭示宏观变形位移特征,但其对揭示细微观破坏机制及岩土体大变形破坏存在缺陷。

颗粒离散元PFC 基于力-位移准则及运动法则,能从细微观角度揭示隧道围岩应力重分布后岩石内部损伤裂纹发展情况,基于大变形计算优势,能揭示隧道岩爆产生区域及方向。从细微观角度及大变形角度揭示岩体隧道变形本质。

1 工程概况及离散元模型参数确定

1.1 工程概况

本数值模型试验是以汾西矿务局南关矿3206 回采隧道为背景,埋深530～650 m,硐室半径为2 m,上覆岩层平均容重约23 kN/m3,静水压力20 MPa,内摩擦角为32°,岩石单轴抗压强度31.8 MPa。岩体内部层理、节理交错、贯穿。在高地应力作用下,隧道岩体变形机理极其复杂,影响隧道开挖安全性。

1.2 离散元基本原理及模型参数确定

颗粒离散元PFC2D,基于两大法则(力-位移准则及运动法则)不断更新颗粒位置及力。

1.2.1 力-位移准则

颗粒离散元模型中,作用于接触模型的力由切向接触力和法向接触力组成:

结合本构模型,可得到作用于颗粒上的合力及合力矩。

1.2.2 运动法则

通过力-位移准则确定了作用于颗粒上的合力和合力矩,而后根据运动法则,可建立颗粒平移和旋转运动方程:

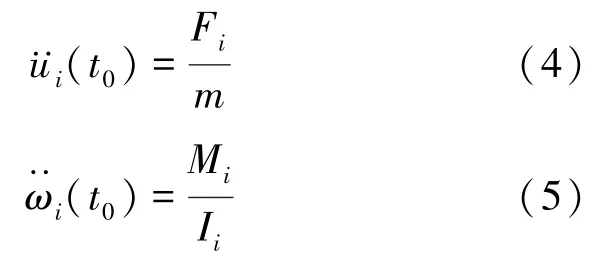
将通过运动法则计算得到的位置信息更新,代入力-位移准则,重新算得作用于颗粒上合力和合力矩[8],如此反复。

与传统有限元及有限差分法不同,PFC2D针对不同岩土特性材料选用不同接触模型。颗粒离散元软件中附带大量接触本构模型,能很好反映砂土摩擦属性的线性模型,不考虑抗转动影响的点接触模型以及考虑抗转动的平行粘结模型及平节理模型,对于模拟岩石内部损伤和节理的光滑节理模型,大量学者研究发现,颗粒离散元细观参数与材料的宏观参数不是一一对应,其中平行粘结模型能较好地反映岩石的力学特性及变形特性[9-10],其本构模型见图1。颗粒受外力作用,当其荷载超过极限荷载时,接触模型中的法向接触强度和切向接触强度同时降为0,模型一般退化成线性接触模型;力矩与转角角度相关,当达到抗弯极限,力矩数值减小为0。

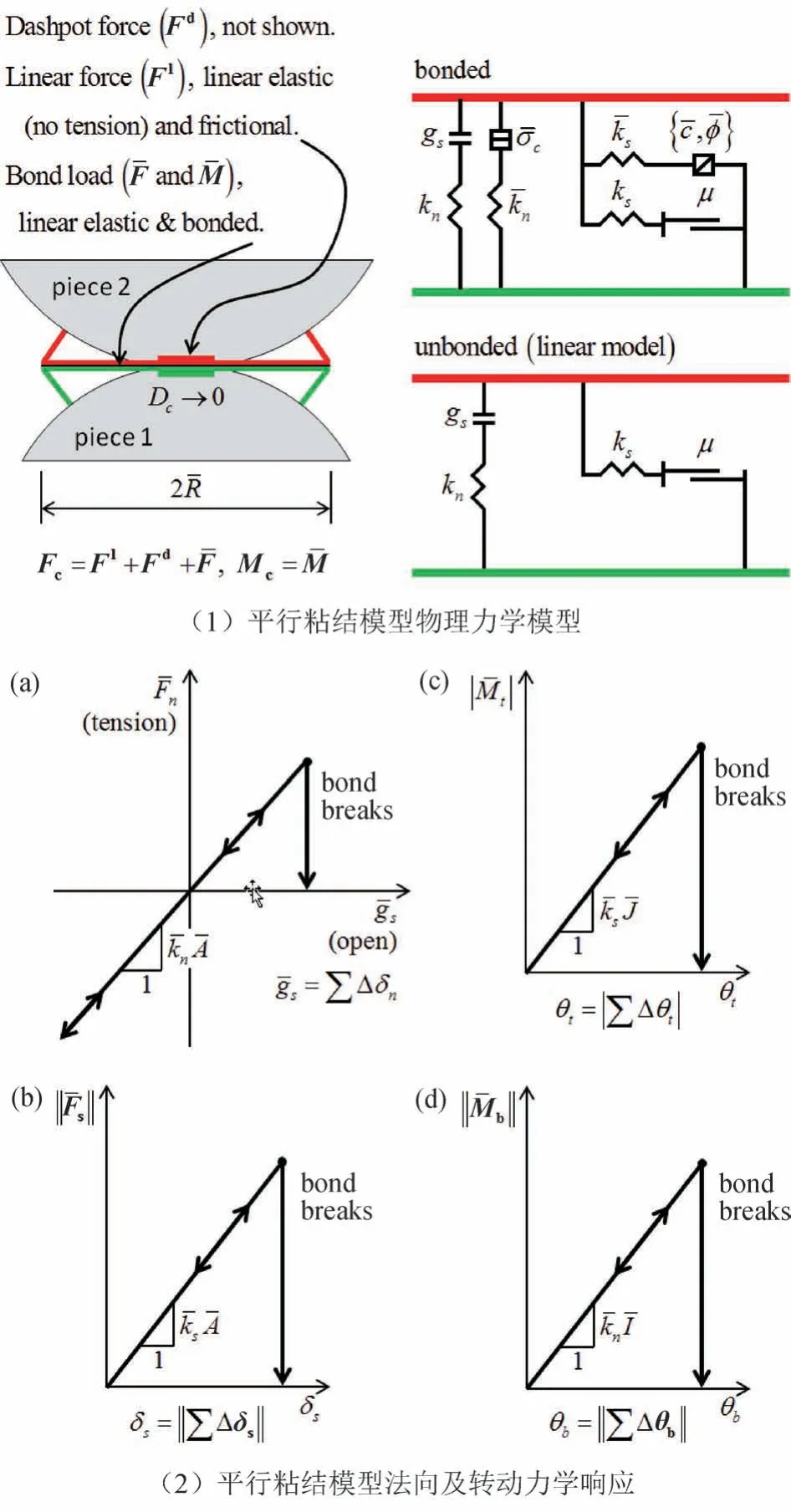
图1 平行粘结本构模型

本文基于室内试验参数,采用试错法获取平行粘结模型细观强度参数,见表1。

表1 DEM 模型细观参数[11]

通过单轴试验验证细观参数准确性,见图2,DEM 单轴试验应力-应变曲线峰值应变及峰值应力与试验数据基本相符,破坏形式符合岩石的单剪破坏形态[12]。宏观参数与DEM 试验力学参数对比见表2,吻合度较高,PFC2D较好地反映岩体变形及力学特性。

表2 宏观参数及DEM 试样力学参数对比

图2 单轴标定应力-应变曲线及破坏形态

2 含不同倾角节理离散元模型建立

基于上文接触模型及细观参数,建立含不同节理隧道模型。研究圆形隧道半径为2 m,考虑尺寸效应,取模型长宽为24 m×24 m。模型边界由四面墙单元组成,通过伺服控制程序,控制边界应力维持在30 MPa。节理模型通过光滑节理模型模拟,考虑到岩体节理密度较大,为揭示节理密集情况下岩体破坏特征,数值模拟中节理间距为3.5 m,研究无节理岩体、节理倾角20°、节理倾角45°及节理倾角70°共4 种工况下的圆形隧道力学及变形演化特征[13-14]。不同节理隧道模型见图3所示。

图3 含不同节理隧道模型

3 离散元模型计算结果

下文主要从变形、裂纹发展情况及径向应力分析不同倾角节理对隧道稳定性影响。

3.1 变形及裂纹发展情况

不同倾角节理岩体变形及裂纹发育情况见图4所示。图5为节理倾角70°局部裂隙放大图。

图4 不同倾角节理岩体变形及裂纹发育情况

图5 节理倾角70°局部裂隙放大图

由图4(a)可知,对于无节理岩体,开挖导致围岩应力重分布,在不考虑结构面情况下,卸载作用下岩体四周应力分布较均匀,裂隙沿临空面较近距离分布,且裂隙发育程度较低。由图4(b)与图4(d)可知,节理倾角20°及倾角70°岩体,变形沿临空面方向分布明显不均匀,且变形量明显高于无节理岩体。由于贯穿节理切割岩体,导致岩体呈现各向异性,在节理与临空面接触处产生应力集中现象,导致裂隙从接触处扩展,不断向岩体内部发育,极大地降低隧道岩体稳定性[15]。由图4(c)可知,节理倾角45°时,岩体向临空面变形较其他角度减小,裂纹发育区域减小。

在高应力作用下,深部岩体极易诱发岩爆作用,对生命财产造成巨大损失。通过分析不同节理下裂纹扩展方式发现裸巷模型,裂纹在临空面分布较均匀,岩石沿隧道周边损伤均匀,应力集中现象有一定程度释放。节理角度为20°及70°时,节理与隧道临空面交界处出现破裂块体,高应力作用下,其交界处应力集中现象明显,发生岩爆作用,岩爆作用均出现于两节理之间。节理倾角为45°时,出现岩爆作用,但其作用强度小于节理倾角为20°及70°隧道。节理角度20°及70°,模型各向异性较大,隧道在节理与临空面交界处的应力集中现象明显,岩爆产生概率增大。

3.2 径向应力情况

从应力重分布角度分析节理对隧道稳定性影响,不同倾角节理岩体径向应力分布见图6所示。

由图6(a)可知,无节理隧道,开挖卸荷作用下,隧道临空面径向应力较大,隧道整体性较完整,与上述裂纹发展规律相符。由图6(b)与图6(d)可知,节理倾角20°及70°隧道,应力重分布后,由于岩石损伤,岩爆作用发生,临空面径向应力衰减严重,隧道处于极不稳定状态。由图6(c)可知,节理倾角为45°时,径向应力一定程度衰减,但仍具有一定支撑作用。

图6 不同倾角节理岩体径向应力分布

图7不同倾角节理径向应力对比,岩体开挖卸荷作用下,对于无节理模型及节理倾角45°,临空面岩体破坏程度较小,临空面岩体较完整,应力较大。节理角度20°及70°岩体,由于岩体各向异性加剧,临空面岩体破坏严重,径向应力严重降低,对隧道支撑作用极大减低,岩体处于不稳定状态。

图7 不同倾角节理径向应力对比

4 多节理对隧道稳定性影响

上述研究了一组平行节理对隧道稳定性的影响,经现场调查及勘察,岩体含有大量面节理,与平行节理贯穿形成多组交错节理,岩石被交错节理切割。在上述研究的45°节理基础下,添加一条模拟面节理的平行节理,研究隧道在多节理状态下稳定性,见图8所示。

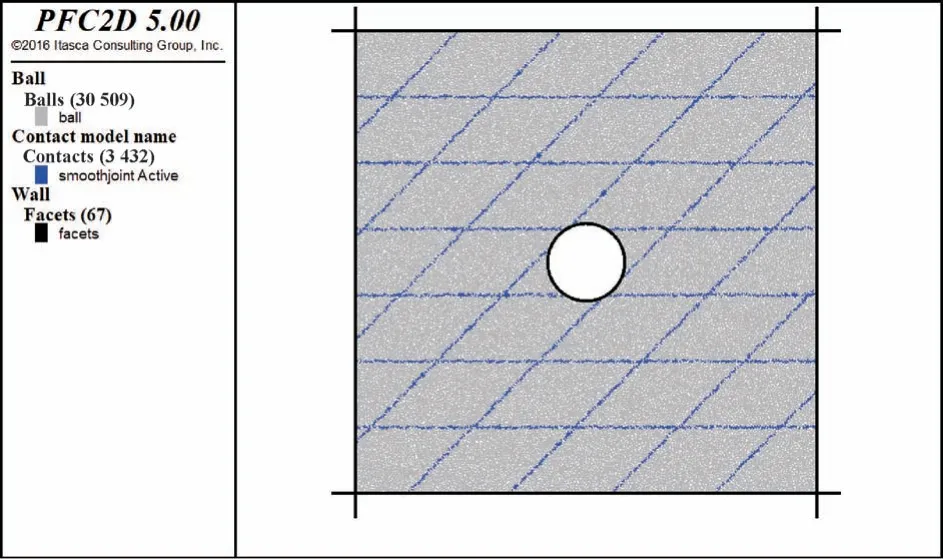
图8 多组交错节理隧道模型

隧道多节理状态下变形及裂纹发展情况见图9。由图9可知,隧道临空面变形大,交界面处裂纹发育剧烈,伴随着岩爆现象,大量块体掉落或倾向隧道空间,岩体处于极不稳定状态。图10 为多节理岩体局部裂隙放大图。

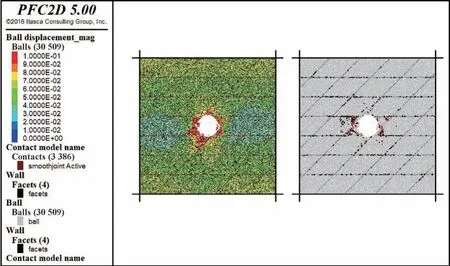
图9 多节理岩体变形及裂纹发育情况

图10 多节理岩体局部裂隙放大图

节理将岩体切割成块体,岩体开挖卸荷作用下,应力重分布,在块体交界处产生应力集中,岩体从卸荷最严重的隧道临空面开始发生损伤,隧道临空面处径向应力急速减低,趋向于0,径向应力最大点向岩体深部移动,见图11 所示。

图11 多节理岩体径向应力分布

由图11 可知,多组节理隧道稳定性极大降低,可从裂纹发育及应力分布情况揭示其机理。由于多层节理对岩体其切割作用,形成的块体交界处产生应力集中,损伤从临空面逐渐向岩体内部扩展,造成隧道失稳。

5 结论

(1)基于颗粒离散元PFC2D建立了不同节理角度岩体模型,在开挖卸荷作用下,从变形及裂隙发展角度揭示了不同节理角度对岩体稳定性影响,揭示了变形机理破坏机理。

(2)节理倾角为20°及70°时,岩体各向异性较大,隧道在节理与临空面交界处的应力集中现象明显,岩体损伤作用明显,岩爆产生概率增大。

(3)随着岩体各向异性较大,岩体沿隧道临空面变形增大,裂隙发育剧烈,不断向内部扩展,径向应力急剧降低,隧道稳定性严重降低。

(4)多层节理对岩体的切割作用明显,其交界处产生应力集中,裂纹从临空面向岩体内部扩展,隧道岩爆作用明显,自稳状态极大降低。