等值电阻法在配电线路线损计算中的应用

郭庆伟, 黄 珊, 郭秀娟, 张 朝

(1. 中国华电科工集团有限公司 环境保护分公司, 北京 100160；2. 吉林建筑大学 电气与计算机学院, 长春 130118； 3. 吉林大学 仪器科学与电气工程学院, 长春 130061)

0 引 言

线损是电力系统中最常见的一种电能损耗形式, 但也是最不可忽视的能量损耗。线损的存在不仅造成能源的浪费, 而且直接对供电企业的经济效益产生影响。因此, 对线损进行理论计算及加强线损管理, 建立合理的线损评估指标具有重要意义[1-2]。

随着电网技术的快速发展, 已有很多成熟的计算线路损耗的方法。目前有关电网理论线损的计算有两类模型： 一类是基于主要网损分量的物理特性建立的模型; 另一类是基于馈线数据的统计模型[3]和神经网络模型[4]。在配电网中, 针对电网结构、 计量设备和计算平台等方面则是在原始的结构和运行数据信息不足的情况下进行近似计算。为此, 笔者根据电网的线损率是整个电网的损失电量与供电量比值的定义, 结合配电网的结构和运行状况, 分析配电网线损的原因, 采用等值电阻法进行配电网电能损耗计算、 分析, 利用算例和实际对比, 其结果表明本研究方法应用于电网企业、 企业自有电网配电线路中, 能有效减少电能损失, 节约成本, 对促进企业经济发展具有指导意义。

1 线损的产生

通过调研、 实际观测和分析, 电网的线损主要是电能通过传输线路传输时产生的能量损失, 而线路损失是由动力传输的有功功率损失引起的, 主要包含以下几部分。

1) 电流产生的有功功率损耗。这是由电流流经导线时产生的有功功率损耗, 是产生线损的主要部分。线路损耗来源于电阻消耗的电压或电能, 由于导线的横截面积和长度决定电阻的大小, 而电流大小决定电压或电能损耗量, 因此通过线路的电流越大, 电压损耗越多, 电能损耗就越大, 并且通过的时间越长, 损耗的功率越大。

2) 绝缘漏电产生的有功功率损耗

ΔPg=U2g

其中ΔPg为绝缘漏电产生的有功功率损耗；U为线路电压；g为有绝缘漏电的电导。

3) 电晕损耗。架空输电线路以及其他高电压电工设备因出现电晕放电而造成的能量损耗。电晕损耗是电力系统运行中的不利因素。

4) 管理线损。在工作中由于管理制度的执行和岗位责任制落实不到位, 出现违反规章制度的情况, 从而造成的损失也是线损之一, 被称为管理线损。

2 常用配电网理论线损计算方法

2.1 均方根电流法

均方根电流法是配电网理论线损计算中最基本、 最常用的方法, 其主要思想是: 均方根电流通过导线产生的能量损失等于同一时间内所有电荷产生的能量损失。计算公式为

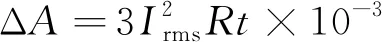
(1)

其中ΔA为损耗电量(kWh);R为原件电阻(Ω);Irms为均方根电流(A);t为运行时间(h)。

该方法的优点是按代表日24 h的整点电流或有功、 无功功率或电量以及电压计算出均方根电流后, 就能计算电能损耗, 方法比较简单。缺点是这种计算其实是一种简化计算, 没有实测负荷记录的配电变压器, 不完全符合实际运行情况[5]。

2.2 平均电流法

平均电流法也称为形状系数法, 其利用均方根电流和平均电流之间的等效关系计算功率损耗。通常, 一个电网中通过电路的平均电流消耗的功率与所有电力负载同时损耗的功率相同。计算公式为

(2)

其中ΔA为损失的电能;R为元件的介质电阻值;t为输电线路运行时间;Iac为线路中电流平均值;K为形态系数。

该方法的优点是计算采用的实际数据获取容易且较为准确, 计算方法简单。缺点是形状系数不易得到, 因此在计算中会简化形状系数的计算, 但将影响电能损耗计算结果的精度。

2.3 潮流前推回代法

潮流法是计算理论线损准确性较好的方法。而较为有效的是支路前推回代法, 以支路网损作为状态量, 进行前推回代法求解[6]。在反向传播过程中, 采用遍历树修改后序列中的节点电流和前序列中的节点电压, 直到满足收敛条件。 每个点电压的真实值可通过迭代计算近似得到。

该方法的优点是容易理解, 收敛性好, 适合编程用于计算机求解。缺点是若电力系统网络的元件和节点数太多, 或运行参数搜集不全时, 则无法使用此方法。

2.4 等值电阻法

等值电阻法适用于运行中配电网络电能损耗计算, 其将配电网络通过元件的有功损耗视为通过配电网线路等值电阻和配电变压器等值电阻所产生的有功损耗, 在配电网线路等值电阻和配电变压器的等值电阻计算出后, 便可求得在某时段内配电网的电能损耗。常用于10 kV电压等级及以下电力系统计算理论线损时。

2.5 电量法

电量法是计算配电网线损的一种精确方法。其利用了各节点的有功功率和无功功率参数, 易于采集, 不考虑各支路的分流。

与传统的电流法相比, 电量法具有精度高、 维护好、 应用范围广、 线损计算方便等优点[7]。 缺点是需要收集大量的有功和无功数据。

3 等值电阻法的计算方法

等值电阻法的基本思想是流经等效电阻的配电网的总均方根电流将导致由等效电阻引起的损耗, 该损耗等于计算出的配电网的所有配电线损耗和负载损耗的总和。利用流经配电网的总有功和无功电量计算总均方根电流, 配电线路等值电阻Rleq和配电变压器等值电阻Rteq组成了配电网线路等值电阻Req, 其结构如图1所示。

图1 配电网等值电阻原理图Fig.1 Schematic diagram of equivalent resistance in distribution network

三者关系如下

Req=Rleq+Rteq

(3)

因此, 全网线损功率为

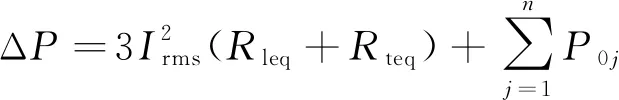
(4)

其中P0j为全网n台配电变压器中, 第j台的空载损耗;Irms为用全网在某时段t内, 有功电能(读表)W和无功电能(度数)Wq计算得出的平均电流Iac与电流形状系数的乘积, 即

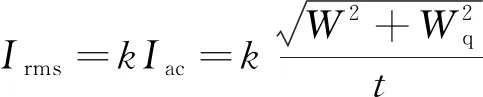
(5)

3.1 配电变压器等值电阻

假设由n台配电变压器构成的电网, 并且设第j台配电变压器的额定容量为Sj, 稳态短路损耗为Pkj, 平均负荷率为kj, 配电网额定电压为UN。则第j台配电变压器的负荷电流为

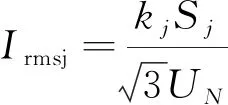
(6)

因此n台配电变压器负荷电流的总和就是全网总负荷电流

(7)

n台配电变压器的负载损耗(功率)总和

(8)

假设全网配电变压器平均负荷率相同, 根据配电变压器等值电阻的定义

(9)

由式(8)、 式(9)可得

(10)

3.2 配电网线路等值电阻

配电网线路是指从降压变电站将电力输送到配电变压器或将配电变电站的电力输送到用电单位的线路。其配电网如图2所示。

图2 配电网示意图Fig.2 Schematic diagram of distribution network

假设电网共分n个节段, 且对应关系为第i个节段的电阻为Ri,Ri后面连接j台配电变压器(j=1,2,…,mi)。流过该节段的负荷电流为

(11)

第i个配线节段的可变损耗为

(12)

其中mi≤m, 并且(m1+m2+…+mn)≥m。

根据全网配电等值电阻Rleq定义可知, 全网配电总损耗

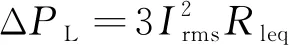
(13)

由此可得全网等值电阻

(14)

假设全网配电变压器平均负荷率相同(ki=k1=k2=…=km), 式(14)变为

(15)

3.3 某时段t内配电网电能损耗

当计算出配电网线路等值电阻Rleq和配电变压器的等值电阻Rteq后, 便可得到时间t内配电网的电能损耗

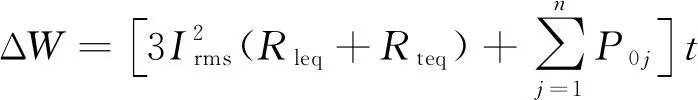
(16)

4 算 例

某10 kV配电网24 h输送电有功电量为25 MWh, 无功电量为20 Mvarh, 最小负荷率为0.33, 平均负荷率为0.56, 线路中有4台变压器, 节段有5段, 长度分别是3 km,2 km,2 km,1 km,1 km。

计算可得

Irms=0.080 21(kA),Rleq=0.828 22(Ω),Rteq=0.822 42(Ω)

线损即电能损耗ΔW为0.832 53(MW·h), 线损率为3.47%。已知实际情况线损率为3.48%, 误差仅为0.01%。

利用Matlab中Simulink仿真算例的配电网部分, 如图3所示。

图3 配电网部分仿真图Fig.3 Partial simulation diagram of distribution network

通过仿真可得出相关数据, 经计算得到线损率为3.47%。

由算例可看出, 虽然误差较小, 但等值电阻法的计算是在假设条件下进行的, 即当负荷的分布与配电变压器的额定容量成正比的前提下, 全网中每个节点的负荷率相同, 每个负荷点的功率因数、 负荷系数和电压相同。由于以上假设在实际情况中是不存在的, 所以, 计算结果的精度一定会受影响。

5 结 语

常见的配电网接线形式有4种： 辐射式、 树干式开环运行的环状干线式和贯通的双干线式配电网。从原理上分析, 等值电阻法只能应用于辐射式配电网计算。但对环网供电, 也可以利用功率分点将其人为的分为两个辐射式配电网。但由于在配电网损耗计算中等值电阻是一个近似的静态模型, 因此在应用中必然有局限。可将等值电阻法进行改进, 考虑负荷不平衡的因素, 或加入潮流计算中的原理, 从而改进等值电阻法, 使其更接近实际应用。