对《六西格玛管理》部分因子试验实例分析的探讨

俞钟行

部分因子（注：以下因子、因素通用）试验可能是应用最为广泛的试验设计，因为许多正交试验就是部分因子试验。本文应用基于excel的“因素趋势法”，可以大幅度削减用Minitab分析的图表，更敏捷地得出更精确的结果。

一、2水平部分因子试验

1.原例7-6“降低硫代硫酸钠产品的杂质率问题”

在硫代硫酸钠生产中发现，影响杂质率的原因有很多，至少有4个因子：成分A含量、成分B含量、反应罐内温度C及反应时间D，而且成分A与成分B在反应中根本不相遇，因而可以认为AB间无交互作用。由于试验成本很高，受限于研究经费只能够安排11次试验。各因子水平分别为：A（低水平12%、高水平16%）；B（低水平2.4%、高水平2.8%）；C(低水平200度、高水平220度）；D（低水平40分钟、高水平50分钟）。

原例采用24-1+3设计，试验方案与结果如表1所示。

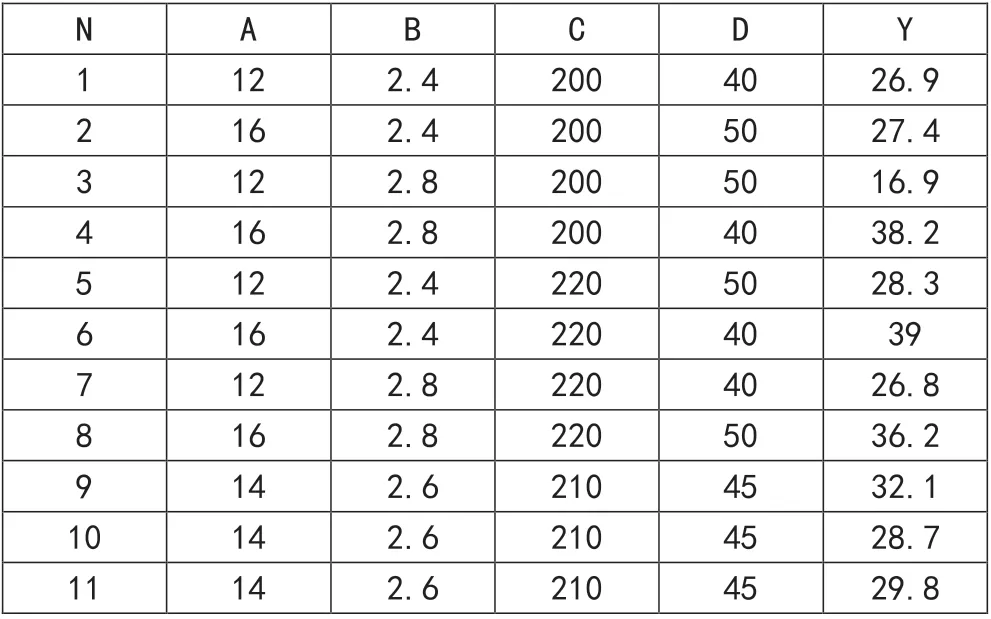
表1 例7-6试验方案与结果

应用“ 五步分析法”，最后得到回归方程：Y= 4 2 4.0 5 2+2.6 1 8 7 5 A-1.9 3 2 C-10.7900D+0.0487500CD；方程的S=1.37155，R-Sq=97.13。

得到最优解为：Y=16.9773、A=12、C=200、D=50。

2.“因素趋势法”求解

（1）仍按原例做11次试验

用excel，画出“因素趋势图”（图1）。

在图1中，因素A力度最强且在趋势上与因素B有强烈的交叉，应当考虑AB有交互作用（这也符合“效应遗传原则”）。但原例中明确强调A与B“在反应中根本不相遇，因而可以认为AB间无交互作用”，这种情况值得认真分析一下。

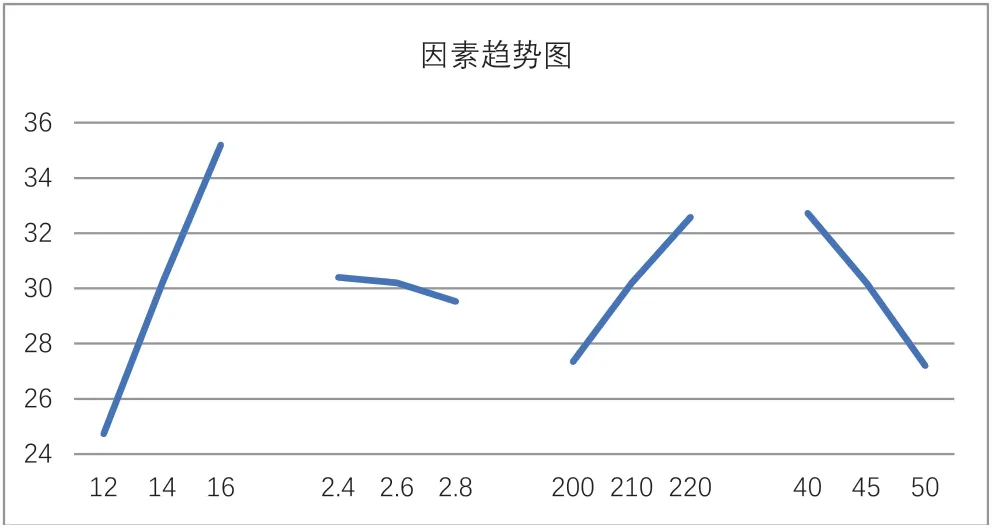
图1 例7-6的“因素趋势图”

下面给出几个文献对交互作用的论述。

《质量专业理论与实务（中级）》（2014年）第100页写道：“在多因子试验中，除了单个因子对指标有影响外，有时两个因子不同水平的搭配对指标也会产生影响。这种影响如果存在，就称为因子A与B的交互作用。”从这可以看出，反应中“相遇”不是交互作用的必要条件，方案中属于不同“搭配”就可以了。

《试验的设计与分析》（刘朝荣，1990）第三章第1节也明确写道：“因素间的交互作用是指因素之间的一种搭配作用。”该书还以22试验为例，记交互作用AB=（A2B2-A1B2- A2B1+A1B1）/2。于是，交互作用就是个数，算出来等于0，无交互作用；不等于0，有交互作用。

最权威的GB/T 3358.3-2009“统计学词汇及符号第3部分：实验设计”中1.17“交互效应”，其定义为“一个因子对响应变量的影响依赖于其他一个或多个因子的效应”。这里讲的“依赖”，并不是一定要在三维立体空间里“相遇”或“碰到”。

几乎大部分文献，都将两个因子的交互作用用图形直观地表示：因素趋势图平行，无交互作用；因素趋势图不平行，有交互作用；因素趋势图交叉越厉害，交互作用也越厉害。

两个有交互作用的因子在何处“相遇”的“悬案”即使未破，也不妨碍试验设计数据分析的进行。因此，对表1的excel电子表格界面插入AB“交互作用”项后，用excel的“回归”模块分析，实际上得到很好的拟合效果。无论是图2里“回归统计”的各项相关系数、标准误差，还是“方差分析”里的Significance F（就是p值）、残差占比（不到2.5%），及最下表的所有因子的p值均小于0.01。

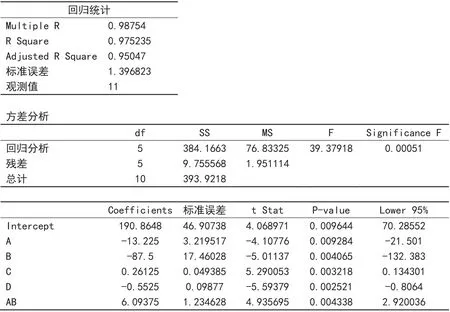
图2 例7-6用“因素趋势法”的回归结果

从图2最下表的Coef f icient s栏，得到回归方程为：y=190.8648-13.225A-87.5B+0.26125C-0.552 5D+6.0 9375AB，方程的S=1.39 6 82 3、R-Sq=0.975235。用excel的“规划求解”模块，得到最优解为：y=16.53977、A=12、B=2.8、C=200、D=50。

与原例的最优方案相比，“因素趋势法”的指标值更优（望小），并包含原例认为是不显著的因子B。在因素趋势法的回归方程里，因子B的p值=0.004065，属高度显著。之所以有这种差别，与数据分析的思路有关。

这里用一个比喻加以解释。把因子或因子的交互作用比作扔在水中的大小不同的石头，若露出水面算因子或因子交互作用显著，否则算不显著。那么可能发生这样的情况：当把所有石头都扔进水中时，水面随之升高，有的石头露不出来；当把最小的几块石头移出水面后，由于水面也相应降低，有的石头就可能露出水面，变成显著的因子了。

（2）只做原例前8次试验

因为用正交表L8（27）成功解决4个2水平因子的试验问题也比较常见，试对原例只做前8次试验。先画出因素趋势图，如图3所示。

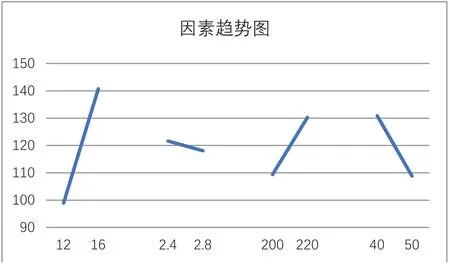
图3 例7-6（只做前8次）的“因素趋势图”

如（1）所作，仍然插入AB交互作用项，并用excel的“回归”模块分析，拟合优度同样出色，如图4。

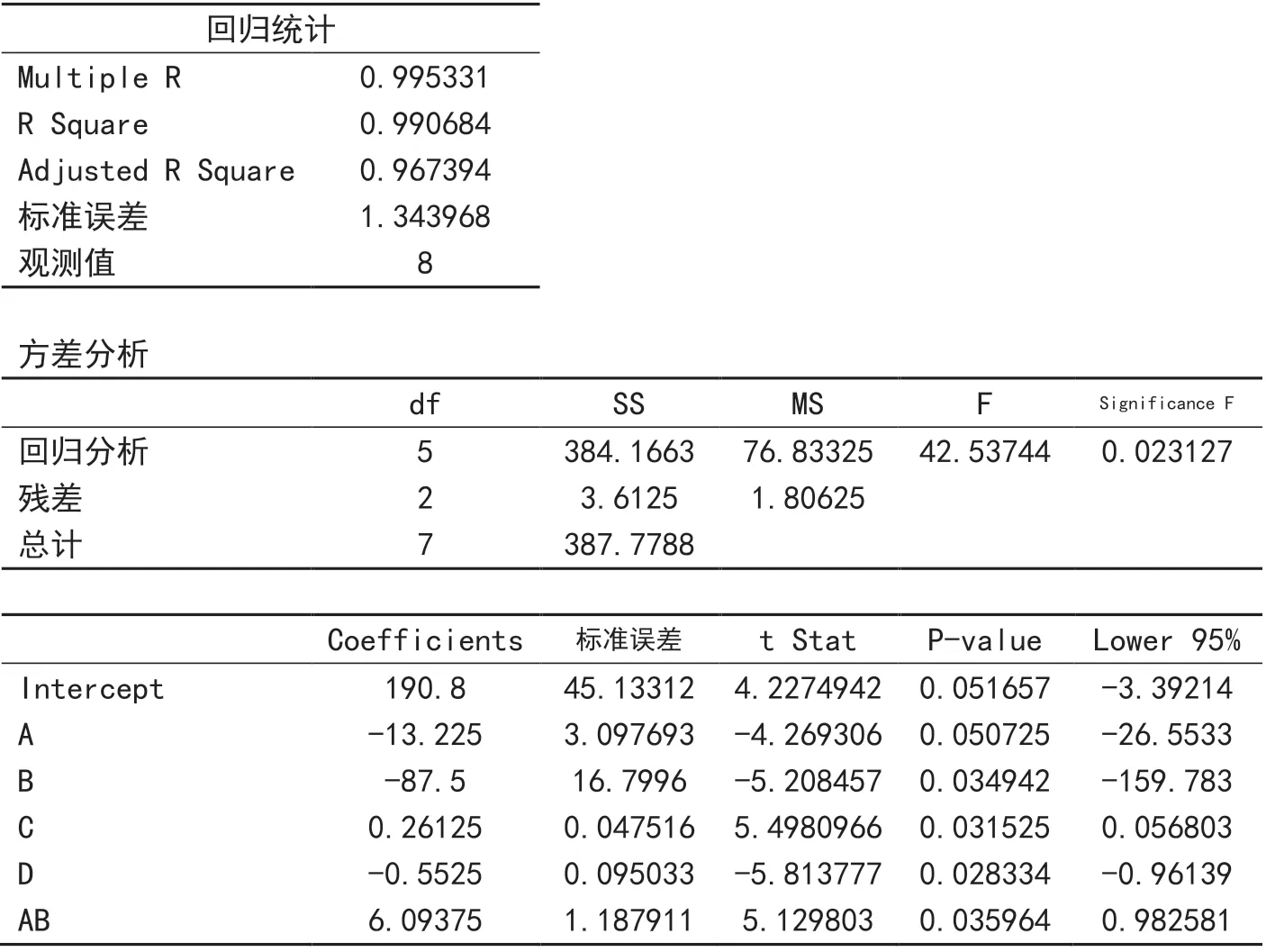
图4 例7-6（只做前8次）用“因素趋势法”的回归结果

最后用“规划求解”得出最优解为y=16.53977、A=12、B=2.8、C=200、D=50。

二、3水平部分因子试验

1.原例7-7“烟灰砖试验”

为了环保，将粉煤灰及煤矸石碾压制成烟灰砖。为了考察如何能使其强度达到最大，要进行试验：把烟灰砖制成边长为15cm的立方体后，将其压碎，以其承载力（kg）为指标y，希望选定最优工艺条件，使y达到最大。共有3个因子选择，其水平如表2。

表2 例7-7因素水平表

原例采用的试验方案与结果如表3所示。

表3 例7-7试验方案与结果

得到回归方程为y=194-5.67A+6.00B-1.33C-18.7A2+5.33B2-9.67C2；方程的标准误差S=2.028、R-Sq=99.4%、R-Sq（调整）=97.6%。

最后因C的p值=0.249，从方程中删去，得到最优解y=205.222、A=0水平（即A=10）、B=1水平(即B=12)、C=0水平（即C=360）。

2.“因素趋势法”求解

在excel的电子表格中，直接以试验数据进入试验方案（表4），并画出因素趋势图（图5）。

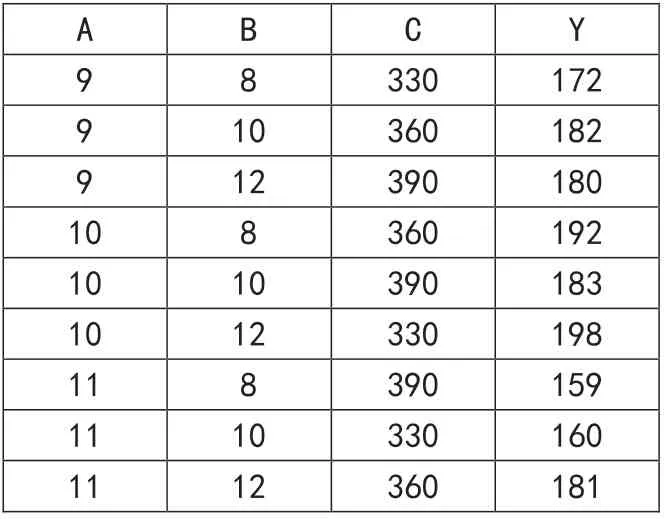
表4 例7-7试验方案与结果（非代码）

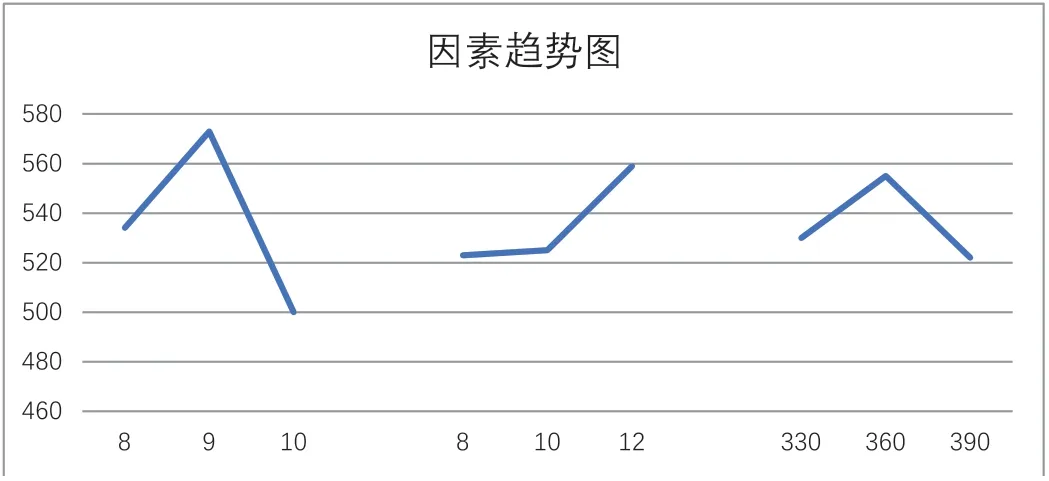
图5 例7-7因素趋势图

根据经验，因子A和C呈角状，是二次项；因子B对照文献[2]的附页，像自然数e的指数状，因此在表中插入A2、C2和eB再进行回归。因为插项后回归的结果中，因子B的p值颇大，为0.674011，故删去。把插项、删项统称为“变项”，最后的电子表格界面与回归结果如表5、图6。

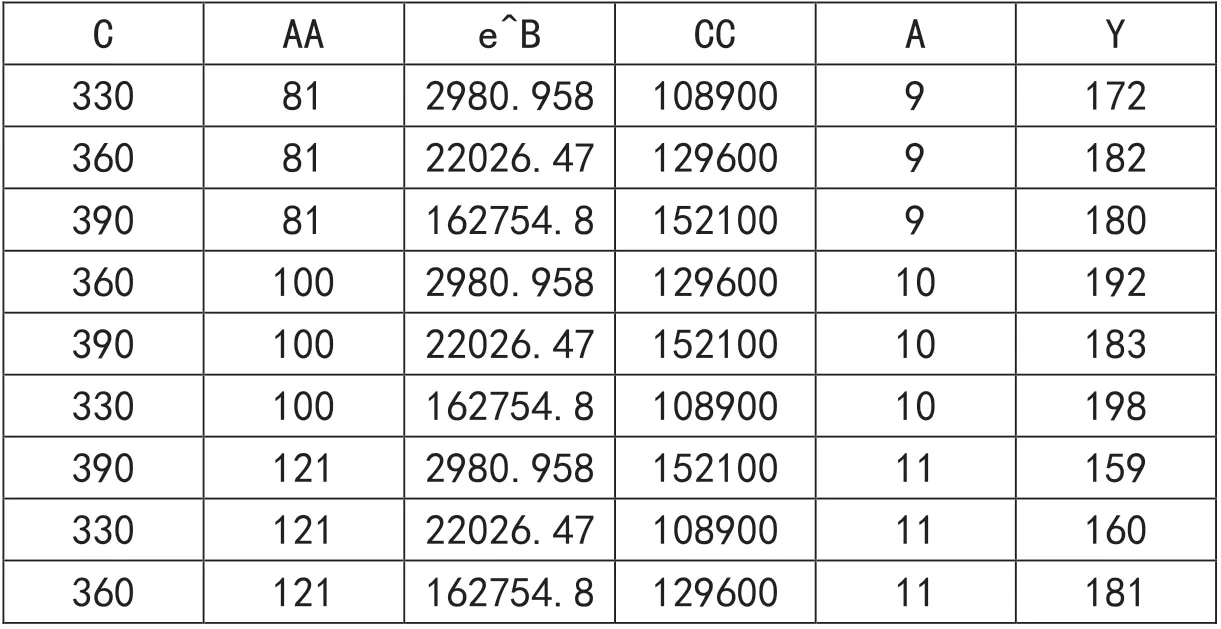
表5 例7-7用“因素趋势法”变项后的excel界面

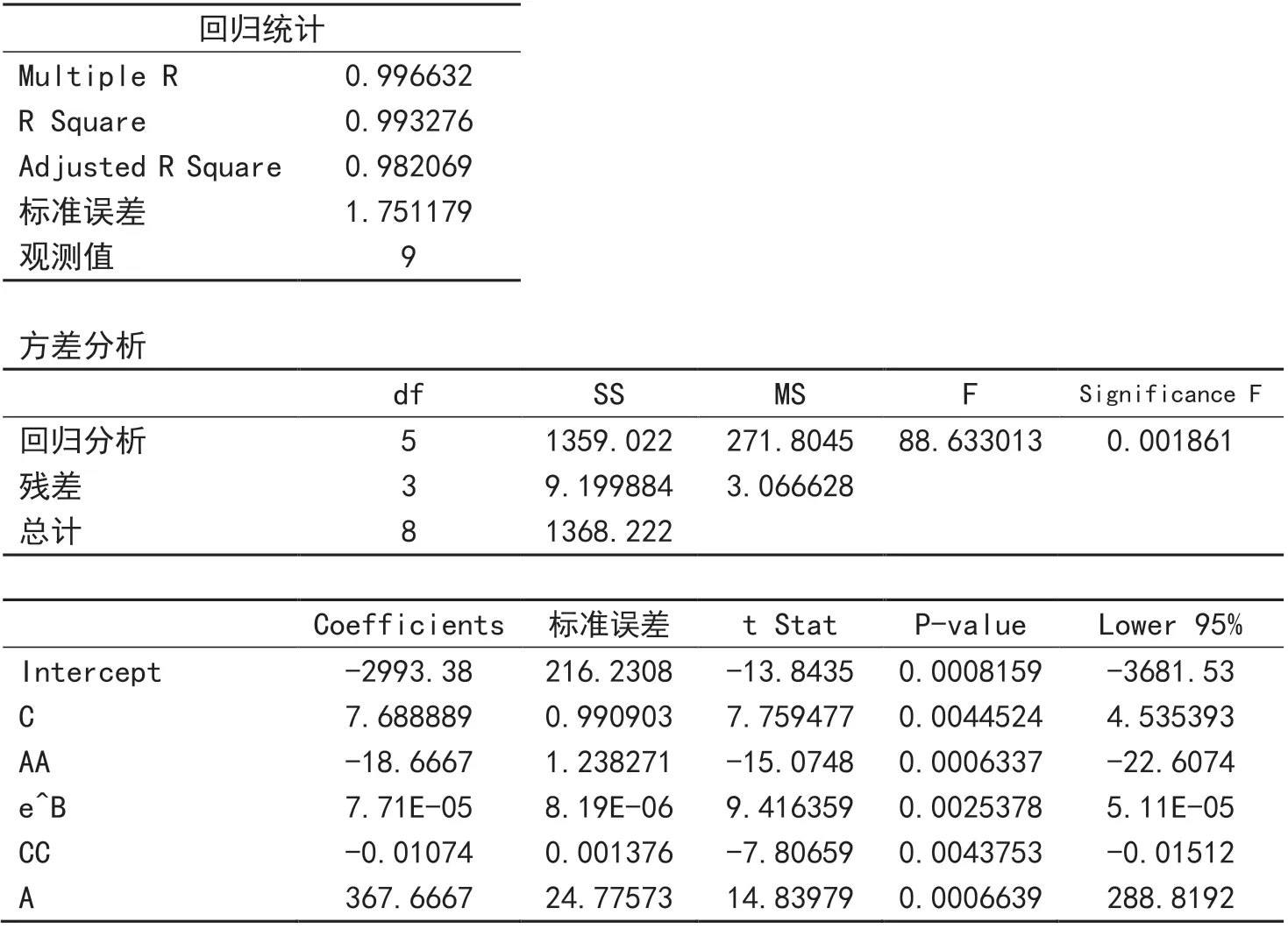
图6 例7-7用“因素趋势法”的回归结果

这里R-Sq=99.3%、R-Sq（调整）=98.2%，与原例的回归方程的对应值相较，十分接近且各有优劣。但这里的标准误差S=1.751179是原来的86.4%，有较大改善。从各项指标看，回归的拟合优度很好，现在得到的回归方程是：y=-2993.38+7.688889C-18.6667AA+7.71E-05e^B-0.01074CC+367.6667A。

最后用excel的“规划求解”模块对方程选优，得到的最优解是y=205.6474、A=9.848215、B=12、C=357.9309。

此例用“因素趋势法”解，从最终结果看，虽有改进但不突出。但此例解法印证了用因素趋势图“导航”来作“精准回归”的方法，是可行的。