基于连续积分法分析高速铁路与中低速磁浮线路交叉跨越对信号电缆的影响*
李天石 龚孟荣 张 晨 黄 辉 苏立轩 霍 斌 王利平
(1.中国铁道科学研究院集团有限公司通信信号研究所,100081,北京;2.中铁第四勘察设计院集团有限公司,430063,武汉∥第一作者,副研究员)
随着中低速磁浮线路的建设发展,多地出现铁路与中低速磁浮线路并行或交叉跨越的情况。例如,建设中的广州清远中低速磁浮线路4次交越铁路(含高速铁路)。这两种交通方式并行和交越时对各自信号系统的电磁影响尚未可知,由此引发了一定的关注与担忧。本文构建了典型的交越计算模型,针对高速铁路与中低速磁浮线路平行与交叉跨越时信号电缆所受电磁影响,进行了理论计算分析和实测验证。
我国电气化铁路对电信线路磁影响互感系数的计算一般采用波拉切克和卡尔生公式[1-2]。对斜接近段和交越段互感系数的计算一般采用分段法[1]。即先分段,再根据1973年CCITT(国际电报电话咨询委员会)发布的《防止电力线路对电信线路危害影响的保护导则》相应表格,求得各段互感系数,最后计算各段感应电动势的和。分段法不仅计算过程繁琐,而且近似误差较大。高速铁路与中低速磁浮线路的牵引供电系统均由多条线缆组成,计算此类强电系统对电信线路的影响时,一般先在其几何位置中点确定1条等效施扰导线,再通过计算确定其上施扰电流的方法。这种方法也存在计算复杂、误差较大的问题。
CCITT曾推荐哈伯尔兰提出的斜接近段和交越段互感系数连续积分计算公式[1-3]。目前我国的铁路防干扰专业未见相关应用。本文采用该法进行计算, 根据线路旁实测磁感应强度反推出等效施扰导线上的施扰电流,综合了强电系统全部导线上电流的作用,改进了分段法的不足,所得结果更符合实际,且更能满足研究需要。
1 电磁影响的计算及参数
1.1 基本感应电动势的计算
当电信线缆与强电线路接近时,电信线缆上感应的纵向电动势E为[1]:
E=2πfIkLpPrPeM
(1)
式中:
f——强电线施扰电流频率;
Ik——强电线施扰电流;
Lp——电信线缆与强电线之间的接近长度,为电信线缆在强电线上的投影;
Pr——铁路钢轨屏蔽系数,对于电气化铁路和磁浮线路,Pr=1;
Pe——电信线缆外皮的屏蔽系数;对于一般铠装铝护套电缆,如电缆外皮双端接地,f=50 Hz,Pe=0.2[1];如外皮单端接地、无屏蔽效果,Pe=1;
M——电信线缆与强电线路间的互感系数,可根据f、大地导电率σ,以及电信线缆与强电线之间的接近距离a计算或查表[1]得出。
1.2 M的计算
1.2.1 以往工程设计采用的方法
在频率和大地导电率确定的情况下,a决定了M的大小。电信线缆与强电线路的接近状态有平行接近、斜接近和交越接近。
如电信线缆与强电线路接近,其始端与强电线路的接近距离为a1,终端与强电线路的接近距离为a2,且a2>a1,其算术平均值a0=(a1+a2)/2。当(a2-a1)/a0≤3%时,电信线缆与强电线路为平行接近。
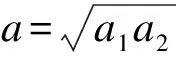
当交越角α>45°时,交越接近段的影响可忽略。交越接近段长度为交越点两侧电信线缆距离强电线路垂直距离50 m的两点之间距离;当α≤45°时,交越接近段长度为交越点两侧电信线缆距离强电线路10 m的两点之间的距离。该交越接近段影响均按a=6 m的平行接近段计算。
1.2.2 连续积分法
为了研究中低速磁浮线路与铁路交叉跨越时相互之间是否存在对信号电缆的电磁影响及这种影响有多大,交越接近段更是关注的重点。在电磁影响分析中,M的分段法有明显不足:①误差较大,当交越角α>45°时交越接近段影响被忽略,当α≤45°时交越接近段影响均按a=6 m的平行接近段计算。②从平行接近、斜接近、到交越接近段,a的取值缺乏连续性。③斜接近段需按a2/a1≤3分成若干段计算,每段a不同、M也不同,计算较繁琐。基于以上原因,本文采用更为适用斜接近段和交越接近段的连续积分法近似计算[1]:
|M|=ln(1+k2/a2)×10-7
(2)
k2=6×106(σf)
其中:k为系数;σ为大地电导率,S/m;a单位为m;M单位为H/m。
为便于计算,设中间变量函数G(a)=aln(1+k2/a2)-2 arctan(k/a)。当a2>a1时,对式(1)—式(2)进行积分,则可得斜接近段的平均互感系数Ma:
Ma=10-7[G(a2)-G(a1)]/(a2-a1)
(3)
由式(1)—式(3),可以计算出强弱电线缆之间不同α、不同高差对应的Ma,便于得出E随各参数连续变化的规律。
1.3 Ik的计算
高速铁路采用的电气化铁路接触网由上下行接触导线、正馈线和架空回流线等组成。中低速磁浮供电线路由上下行供电线缆和馈送与回流接触轨组成。可见,强电线路结构较复杂,仅靠设等效施扰导线的计算法复杂且准确性低。对此,本文引入等效施扰导线和等效施扰电流的概念:用1根流过等效施扰电流Ik的等效施扰导线替代1组强电线,则在距等效施扰导线一定距离的观测点,会产生与被替代的1组强电线相同的感应效果。根据安培环路定律,采用反推的方法即可获取Ik。具体方法如下:
采用低频磁场测量仪,探头距地面高度为1.5 m,测量距电气化铁路或距磁浮线路外轨中心线一定距离处的低频磁感应强度B,并记录f=50 Hz时的低频磁感应强度最大值。则强电线路等效施扰导线电流应满足:
(4)
式中:
R——等效施扰导线距轨旁磁感应强度测点距离;
Ik——等效施扰导线电流;
μ0——真空磁导率,μ0=4π×10-7Tm/A;
由式(4)可推算出Ik。
1.4 导线与电缆位置
1)等效施扰导线位置。对于复线电气化铁路,接触网的等效施扰导线平行于铁路,其轨面以上垂直高度取值见图1,水平位置取复线中心;对于中低速磁浮线路,等效施扰导线也平行于平行线路,其高度与供电导轨轨面高度相同,水平位置取复线中心。
2)磁浮与铁路信号电缆位置。磁浮信号电缆平行于磁浮线路,高度取磁浮导电轨高度,水平位置中心与磁浮复线中心重合。铁路信号电缆平行于铁路线路,高度近似取轨面高度,水平位置在边轨中心线外侧约1.8 m。
强电线路等效施扰导线和被影响导线的几何位置确定后,R与a便可随之确定。
2 典型交越条件下的影响计算
2.1 典型交越条件的设定
典型交越中,磁浮线路下穿和上跨铁路的位置关系见图1。为便于比较,需统一设定典型交越条件下各种交越情况的部分参数:① 铁路或磁浮信号电缆长度L=1 000 m;② 磁浮线路与铁路交越点位于信号电缆中间点;③α=0°~90°;④σ=0.1 S/m;⑤ 计算频率为强电线频率,f=50 Hz;⑥ 铁路信号电缆Pe=1.0,磁浮信号电缆Pe=0.2;⑦ 根据高速铁路线路和中低速磁浮线路在列车通过时B的实测值,计算出Ik。
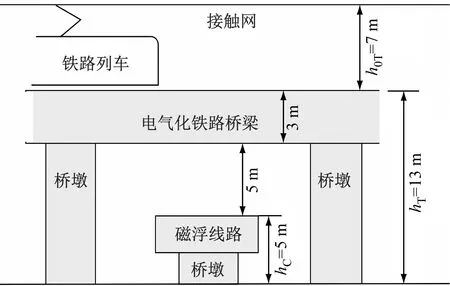
a)磁浮线路下穿铁路
经比较,高速铁路线路的B采用列车速度达300 km/h以上的京沪(北京—上海)高速铁路实测数据。高铁磁场测点距线路外轨中心线水平投影dX=20 m,桥高(轨面至地面高度)hT=10 m,可推出接触网等效施扰导线与地面测点的距离R=28.2 m。实测京沪高铁列车通过时f=50 Hz,磁感应强度B=1.501 μT,由式(4)可推出铁路接触网等效施扰导线上的Ik=211.64 A。
中低速磁浮线路的B采用长沙中低速磁浮线路实测数据。长沙磁浮线测点距外轨中心线水平投影dX=15 m,桥高(导电轨至地面高度)hC=5 m,可推出R=17.9 m。实测磁浮列车通过时f=50 Hz,B=0.022 057 μT,由式(4)可推出Ik=1.975 A。
2.2 典型交越条件下的E
由图1,可分以下4种情况计算信号电缆上某点的a值:
情况1 磁浮线路下穿铁路,磁浮线路信号电缆受铁路接触网的影响。设磁浮线路信号电缆某点在铁路等效施扰导线上水平投影距离为dT,则该点a为:
(5)
情况2 磁浮线路下穿铁路,铁路信号电缆受磁浮线路供电线路的影响。设电气化铁路信号电缆某点在磁浮等效施扰导线上水平投影距离为dC,则该点a为:
(6)
情况3 磁浮线路上跨铁路,磁浮线路信号电缆受铁路接触网的影响。此情况下a为:
(7)
情况4 磁浮线路上跨铁路,铁路信号电缆受磁浮线路供电线路的影响。此情况下a为:
(8)
将由式(5)—(8)得到的a和其他设定参数代入式(1)—(3),计算E,结果见图2。

a)情况2及情况4
由图2可知:① 信号电缆上的E随着α的增大而变小。α=0°时,两线为平行接近,E达到最大;α=90°时,两线为垂直交越,E=0。② 磁浮线路信号电缆受铁路接触网的影响要明显大于铁路信号电缆受磁浮线路供电线路的影响,主要原因在于铁路50 Hz时的Ik(为211.64 A)明显大于磁浮线路50 Hz时的Ik(1.98 A)。③ 由于供电线缆与信号线缆之间距离不同,对于磁浮信号电缆受铁路接触网的影响,磁浮上跨铁路的影响要大于其下穿铁路的影响;对于铁路信号电缆受磁浮线路供电线路的影响,磁浮线路下穿铁路的影响要大于其上跨铁路的影响。
2.3 典型条件下σ变化对计算结果的影响
本文以情况3为例,计算不同σ条件下的磁浮线路LEU(地面电子单元)信号电缆的E值。计算结果表明,σ越小,E越大。如果LEU信号电缆按最长为3 500 m考虑,当α≈0°时,在σ分别为0.1 S/m、0.01 S/m和0.001 S/m时,E分别达到39.5 V、50.2 V和60.9 V,已接近或超过GB 6830—1986《电信线路遭受强电线路危险影响的允许值》中正常条件下E≤60 V的规定。
3 实例计算结果与实测结果的比较
3.1 计算结果
长沙磁浮线与沪昆(上海—昆明)高速铁路交越点位于长沙磁浮线榔梨站北侧300 m处,α=73°。跨交越点的磁浮线路LEU信号电缆长552 m,榔梨站距交越点300 m;交越点至磁浮线路上应答器终端长度为252 m。该信号电缆在铁路线上的投影即为强弱电导线的接近长度Lp。采用本文方法进行计算,当长沙磁浮线下穿沪昆高速铁路时,磁浮线路LEU信号电缆受高速铁路影响,E=174.3 mV。由于磁浮LEU信号电缆较短,α较大,故计算得出的E较小。
3.2 实测结果与计算结果
在距两线交越点最近的榔梨站信号机房(即计算测点处),实地测量了磁浮线路的LEU信号电缆受沪昆高速铁路过车影响产生的、较为稳定的、50 Hz情况下的E值。测量结果见表1。
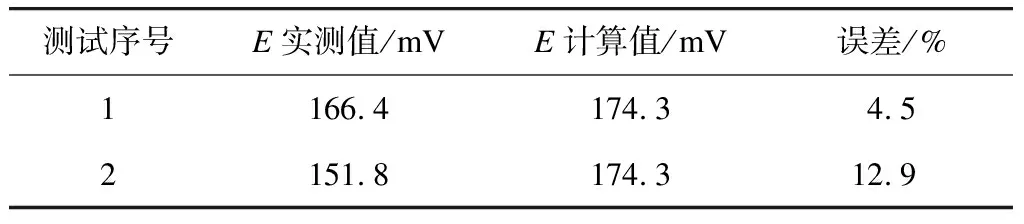
表1 沪昆高铁列车通过交越点时磁浮LEU电缆50 Hz感应电动势实测值与计算值比较
由表1可见,E的实测值与计算值有较好的符合性。计算值略大于实测值,这与计算时某些参数取值存在误差有关。
4 结论
1)信号电缆上50 Hz时的E随着α增大而变小。α=0°为平行接近,E最大;α=90°为垂直交越,E=0。
2)铁路50 Hz时的Ik明显大于磁浮50 Hz时的Ik。磁浮线路信号电缆受铁路接触网的影响要明显大于铁路信号电缆受磁浮线路供电线路的影响。在强、弱电导线接近平行时(α=1°),前者E最大值为10.23 V;后者E最大值仅为0.44 V。
3)对于铁路信号电缆受磁浮线路供电线路影响,磁浮线路下穿铁路时的影响要大于其上跨铁路时的影响;对于磁浮信号电缆受铁路接触网的影响,磁浮上跨铁路时的影响要大于其下穿铁路时的影响。在各交越条件中,磁浮线路上跨铁路是其信号电缆受影响最大的一种交越模式,此时的磁浮信号电缆距铁路接触网距离最近。
4)在较严酷的条件下,即α≈0°时,σ很小,如磁浮线路上跨铁路,受铁路过车影响,则磁浮信号电缆的E有可能接近甚至超过GB 6830—1986中正常条件下的规定值。
5)由长沙磁浮线与沪昆高速铁路交越处的实际α、Lp和Ik,计算得到的磁浮信号电缆E值与实测值基本吻合,验证了本文所采用的计算方法是可行的。
5 建议
根据计算结果及实测情况,工程设计中宜避免磁浮上跨铁路方案,尽量采用铁路上跨磁浮线路的方案;应尽可能增大磁浮线路和铁路的交越角;两者平行接近时,应尽量增大接近距离,减少接近长度;磁浮信号电缆外皮应双端接地。

