基于Dropout法优化的BP神经网络地铁列车塞拉门故障检测

郭井宽

(中国电气装备集团科学技术研究院有限公司，200436，上海∥高级工程师)

地铁列车塞拉门结构复杂、零件繁多、检修工作量大，难以发现其诸多故障隐患。一旦发生塞拉门故障，就会严重威胁地铁列车的安全运行。当前主要由检测工人在列车停运时通过对塞拉门内部组件的检测，来诊断塞拉门故障。但人工检测结果受检测工人熟练程度的影响较大，且对微小故障的检测难度大，易遗漏车门故障隐患，从而导致地铁列车在运行过程中发生故障。2017年，上海地铁列车在运行中曾发生未能正常关闭车门即属于此类故障。

地铁列车塞拉门故障的在线检测研究在国内外尚属新兴的领域。研究学者利用相关历史数据结合故障树技术[1-2]、贝叶斯网络[3]搭建了众多应用于地铁列车塞拉门故障检测的模型。文献[4]利用故障树技术；文献[5]利用贝叶斯网络都对地铁车门可靠性进行了分析；文献[6]建立了基于扩展Petri网的地铁车门系统故障诊断模型；文献[7]利用声音信号易于采集的优点，提出了一种基于多向邻域保持嵌入算法和改进粒子群优化的混合核SVM(支持向量机)算法的列车塞拉门故障诊断模型。这些模型在很大程度上克服了人工检测的缺点，便于相关工作人员及时定位故障与排查，降低故障损失[8]，为地铁列车塞拉门的日常维护工作提供了依据[9]。然而，目前的诊断模型很少涉及到下挡销及压轮故障等塞拉门典型故障的检测，我国在相关领域的研究仍较少。文献[10]对地铁列车塞拉门下挡销及压轮故障的检测进行了相关研究，通过对电机电流进行经验模态分解、奇异值分解等分析处理来提取原始电流信号的特征，并结合支持向量机算法实现了对地铁列车塞拉门下挡销及压轮故障的较高精度的检测。但其数据处理过程较为复杂，检测精度还可进一步提高。

本文通过仔细分析电机电流信号发现：虽然在原始的电机电流时域信号中，下挡销及压轮故障的特征差异不明显，但对电机电流信号进行一定的预处理后，不同状态下的时域波形存在着较为明显的差异；对不同状态下的电流数据提取合适的时域特征，即能实现对不同故障类型的分类。基于上述分析，本文通过提取电机电流信号的时域特征，基于Dropout法优化的BP(后向传播)神经网络理论，建立了一种地铁列车塞拉门下挡销及压轮故障的检测模型。利用实测塞拉门电机电流数据对该方法检测。结果表明，该方法可在地铁列车塞拉门下挡销及压轮故障的实际检测中获得较为优异的效果。

1 地铁列车塞拉门典型故障检测理论

通过车辆段现场实际调研，综合分析车辆段历史维修记录数据发现，在塞拉门系统中下挡销及压轮出现故障的频次相对较高，在塞拉门系统故障中较为典型。因此，本文选用下挡销故障及压轮故障作为本文故障诊断的研究对象，开展相关故障诊断研究。

1.1 下挡销及压轮故障检测机理与路线

地铁列车塞拉门的下挡销部件和压轮部件分别如图1及图2所示[10]。

图1 塞拉门下挡销示意图

图2 塞拉门压轮示意图

当列车车门执行开关动作时，电机输出的动力最终传递到丝杆上，使丝杆在转动的同时带动车门水平移动。在正常状态下，下挡销随着塞拉门的关门动作在挡块滑道中做无接触运动，并在关门到位后起固定门页的作用。而当下挡销发生故障与挡块滑道发生接触时，会引起关门过程中的局部阻力异常，产生一定的反向力矩，并通过塞拉门内部机械传动结构反作用于塞拉门的驱动电机，使作为主动机构的电机产生异于常态的波动力矩[11]，同时导致电机电流发生与之相对应的变化。塞拉门压轮部件在正常工作时，压轮仅在末端啮合对门扇进行压紧，并不会对车门产生阻力。但当压轮位置发生偏移并产生干涉时，同样会引起开关门过程中的局部阻力异常，并反作用于塞拉门驱动电机，导致电机电流产生与之相对应的变化。因此，通过将电机电流信号作为原始数据进行分析，基本能实现对塞拉门下挡销及压轮的故障检测[10]。

基于上述理论，本文将不同状态下的电机电流信号的差异性作为故障判断的依据，对在正常、下挡销故障及压轮故障三种状态下的电机电流进行数据预处理及时域特征提取，并将之与BP神经网络模型相结合，结合Dropout算法完成对模型的训练，最终建立塞拉门下挡销及压轮的故障检测模型，实现对地铁列车塞拉门下挡销及压轮的故障检测。故障检测实现路线如图3所示。

图3 故障检测流程图

1.2 特征提取及分析

当前，对不同状态下电机电流信号的时域分析主要采用平均幅值、均方根、最大值、方差、波形因子、脉冲因子、峭度因子等统计指标来表征数据特性。部分时域分析常用的特征参数如表1所示。

表1 部分时域分析常用的特征参数

在对电机电流信号的时域分析中发现，在对电机电流信号的时域数据进行一定的预处理后，不同故障状态下的电机电流数据在时域上的波形存在较为明显的差异。这种差异在关门过程末端的时域波形上体现得最为明显。因此，对电机电流信号可提取其时域特征进行分析。筛选出峰值附近的电机电流数据进行时域分析，对其采取幅值量纲一化、取波形包络等预处理，并进行时域特征提取，之后将所提取的特征参数作为BP神经网络模型的输入变量，以完成故障检测模型的搭建。

此外，由于地铁列车塞拉门下挡销及压轮故障检测的复杂性及先验知识的不充分，在开始阶段一般难以直接确定与故障检测最相关的特征。因此，需要对时域特征进行筛选以获取合适特征。由于箱线图不仅能反映单组数据的分布情况、异常值、波动情况、稳定性，还能对比不同类别的数据在分布上的差异。因此，本文通过不同状态下所提取到的时域特征数据的箱线图，来对比不同状态下的时域特征的差异，最终选定合适的时域特征作为BP神经网络模型的输入。

1.3 BP神经网络模型原理

BP神经网络模型是一种利用梯度下降算法反向调整权重的多层神经元构成的前馈人工神经网络模型，其结构如图4所示。BP神经网络模型的训练学习过程分为两个阶段，第一阶段是输入信息前向传递，信息通过前向网络逐层前进，分散传输到各层神经元，经过处理后，将实际结果输出；第二阶段是结果误差反向传播，通过更改模型中的权重使得网络输出结果和期望值之间的均方误差达到最小，最终获得高精度的拟合结果。

图4 BP神经网络结构示意图

BP神经网络模型的具体训练学习过程如下：

输入信息正向传递过程：首先，输入样本数据到输入层神经元，使样本信息进入神经网络中，隐含层的各个神经元对多个样本数据进行非线性运算处理；然后，通过输出层将结果输出，并与己知的结果进行比较。通过设定阈值范围，判断计算输出结果与已知结果的误差是否在阈值范围内：如果在阈值范围内，则算法训练结束；如果超出设定范围，则进行误差反向传播。

结果误差反向传播过程：首先，将总误差从输出层输入，即可实现结果误差进行反向传播；经由隐含层神经元对误差进行反向映射，将误差传到输入层。这一过程是利用梯度下降算法将总误差分散到各个神经元，用以大化小的思维一层一层地修改权重。

此处以典型的3层BP神经网络进行说明，设输入层的输入向量为I=(I1I2…Il)，其中l表示输入层包含的节点个数。此处加入“常数项输入”x0=1，并为其赋权值w0j。输入层的输入值即为其输出值。设隐藏层获得的输入向量h=(h1h2…hq)，输出向量t=(t1t2…tk)，其中q是隐藏层神经元的个数，则有：

(1)

式中：

i——输入层包含的各节点编号，i=1,2,3,…,l；

j——隐藏层包含的各节点编号，j=1,2,3,…,q；

wij——输入层第i个神经元到隐藏层的第j个神经元之间的权重。

且有隐藏层的输出值为：

(2)

设输出层输入向量z=(z1z2…zn)，输出向量y=(y1y2…yn)，其中n是输出层包含的节点个数。则有输出层的输入值和输出值类似于隐藏层的输入值和输出值，分别为：

(3)

(4)

式中：

vjk——隐藏层第j个神经元到隐藏层的第k个神经元之间的权重。

设d=(d1d2…dl)为期望输出，而实际输出为y=(y1y2…yn)，则BP神经网络的实际输出向量y与期望输出向量d之间的误差可表示为：

(5)

对于隐藏层则有：

(6)

对于输入层则有：

(7)

由式(7)可知BP神经网络的误差是关于各层连接权值wij、vij的函数，因此可通过对各层连接权值的修正降低误差，各层误差修正则是通过误差函数对各节点的求导进行确定。

对于输出节点对误差函数求导有：

(8)

其中：

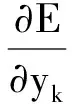
(9)

(10)

则有：

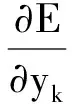
(11)

对于隐层节点对误差函数求导有：

(12)

其中：

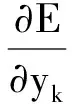
(13)

(14)

(15)

则有：

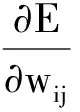
(16)

为简化公式，令

δk=-(dk-yk)f′(zk)

(17)

δj=δkvjkf′(hj)

(18)

则有：

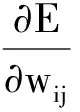
(19)

权重的修正量Δwij、Δvij同误差函数的负梯度方向成正比，则有：

(20)

vjk(m+1)=vjk(m)+Δvjk=vjk(m)+ηδktj

(21)

(22)

wij(m+1)=wij(m)+Δwij=wij(m)+ηδjxi

(23)

式中：

wij(m)——第m次迭代时输入层第i个神经元到隐藏层的第j个神经元之间的权重；

wij(m+1)——第m+1次迭代时输入层第i个神经元到隐藏层的第j个神经元之间的权重；

vjk(m)——第m次迭代时隐藏层第j个神经元到输出层的第k个神经元之间的权重；

vjk(m+1)——第m+1次迭代时输入层第j个神经元到隐藏层的第k个神经元之间的权重。

BP神经网络通过以上方式不断地进行信息前馈和误差反馈，随时调整权重，直至训练学习收敛。训练学习收敛方式一般有设定误差阈值及设定训练次数两种。当满足其中1种方式的收敛条件时，BP神经网络模型就被训练好了。

1.4 BP神经网络模型的优化

在机器学习的模型中，如果模型的参数太多，而训练样本又太少，则训练出来的模型很容易产生过拟合的现象。本文所选用的数据存在着数据量较少的问题，因此最终训练所得的模型可能存在着过拟合的情况。为避免出现这类情况，本文在训练模型时采用Dropout法[12]对BP神经网络模型进行优化。

Dropout法是解决BP神经网络在训练学习过程中出现过拟合的有效方法，是指在深度学习网络的训练过程中，对于神经网络单元，按照一定的概率将其暂时从网络中丢弃，其原理图如图5所示。

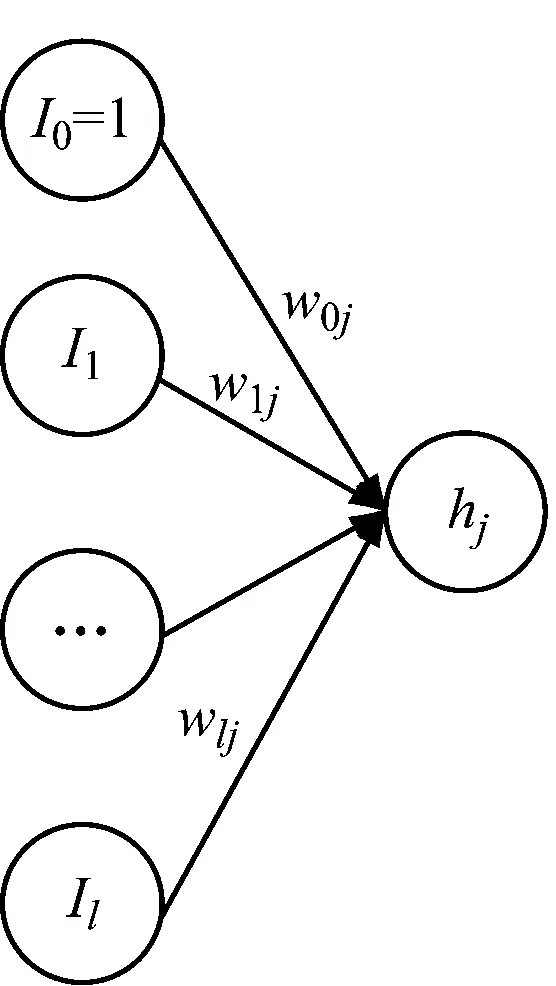
a)原始网络

则式(1)应变形为：

(24)

式中：

rij——前层第j个神经元到后层第i个神经元对应的伯努利函数，在本文中特指输入层到隐藏层。

采用Dropout法对BP神经网络模型进行优化的具体的训练步骤如下：

步骤1 在训练之前按照预设的几率抛弃部分隐藏层的神经元，暂时不让其涉及到正向传递，输入和输出层的神经元保持不变。

步骤2 将样本数据在结构已经改变的BP神经网络中进行传递，所得到的误差在结构变化后的 BP神经网络再反向传播，同时更新BP神经网络的权值和阈值。

步骤3 重复上述步骤1及步骤2，直至迭代完成。

2 实际案例测试

2.1 数据来源及特征提取

本文使用的塞拉门电机电流数据来源于某地铁车辆段现场实测数据。1次开关门过程中的单相电机电流数据为1组试验数据。其中1组原始试验数据如图6所示。图6中，0～5.5 s为开门阶段，5.5～11.0 s为关门阶段。

a)正常状态下的电机电流信号

由图6可知，原始电机电流信号在下挡销故障、压轮故障等不同状态下难以直接区分。但通过对不同状态下的电机电流信号在关门阶段后期(图6虚线所圈出区域)的信号进行去噪及幅值量纲一化等预处理后，不同状态下的电机电流信号则呈现较为明显的区别。其中1组经过去噪及幅值量纲一化等预处理后不同状态下的电流信号包络线及波形图如图7—图9所示。

图7—图9中横、纵坐标分别为时间采样点和电流的幅值，突出波形分别为截选出的原始数据绝对值波形和取峰值包络后的对应包络波形。在完成对数据的峰值包络后，本文再按照表1对包络波形提取其时域特征，完成对数据特征提取操作。

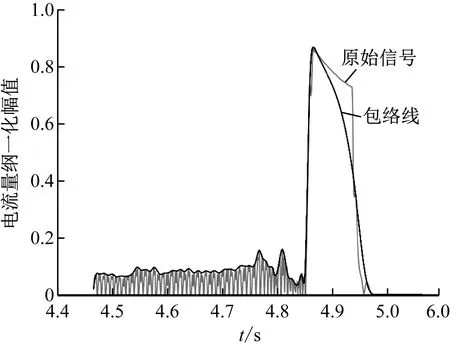
图7 正常状态下电机电流信号的包络线及波形图

图8 下挡销故障下电机电流信号的包络线及波形图

图9 压轮故障下电机电流信号的包络线及波形图

2.2 输入特征分析及筛选

按表1，计算不同状态下电机电流信号的时域特征数据，并绘制相应的时域特征箱线图(见图10)，以对比其分布差异性。

从图10可知，在不同状态下：时域特征中方差、最大值、波形因子、平均幅值、脉冲因子等时域特征参数的分布差异较大；峭度因子、均方根的分布差异较小。因此，本文选取电机电流的方差、最大值、波形因子、平均幅值及脉冲因子作为BP神经网络的输入参数。

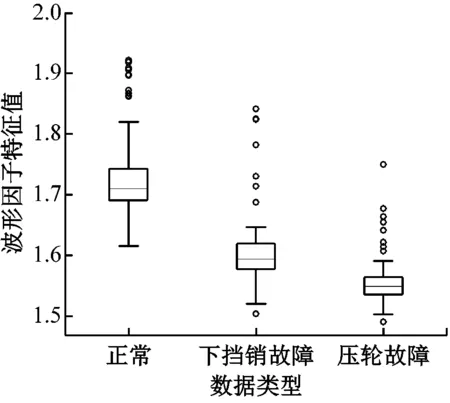
a)波形因子箱线图

2.3 BP神经网络的结构设计

BP神经网络模型结构对塞拉门下挡销及压轮的故障检测有着至关重要的影响，应合理选择。本文的BP神经网络模型结构设计如下：

1)神经网络层数。根据实际情况，本文选择了含有1层隐藏层的3层BP神经网络模型结构，来完成塞拉门下挡销及压轮故障的检测。

2)输入层神经元数目。基于时域特征分析，本文选择了电机电流信号的均方根、波形因子、峭度因子、最大值、方差等时域特征参数来表征时域特征。相应的输入层神经元数目确定为5。

3)输出层神经元数目。输出层神经元数目是由实际需求来确定的，其与故障检测最终分类结果的类型数目有关。本文的输出层神经元数据标签分为正常、下挡销故障及压轮故障3类，故输出层神经元数目确定为3。

4)隐藏层神经元数目。隐藏层的神经元个数过多，可使神经网络结构变得复杂，从而获得良好的训练效果，但是会出现收敛缓慢、训练时间长等现象，在测试时会造成误差精度和识别率下降。相反，如果神经元个数太少，则使神经网络结构过于简单，不能有效利用样本数据，出现欠拟合现象，精度降低，训练结果较差，从而不能用于与经过几种估算公式计算的结果作比较。最终，本文隐藏层神经元数目确定为9。

5)学习率及Dropout值。在用于故障检测的BP神经网络的最终实现中，学习率一般取值为0～1。本文通过调用scipy.optimize数据库中的minimize函数自动选择学习率。此外，Dropout值一般取0.3～0.5。本文根据经验将Dropout值取0.3。

2.4 预测结果及模型性能评估

本文以模型预测精度作为模型性能的主要评估指标。对未经Dropout法优化的BP神经网络故障检测模型(以下称为“模型一”)，以及经过结构合理设计及Dropout法优化的BP神经网络故障检测模型(以下称为“模型二”)，均采用同一训练数据对模型参数进行更新，并通过测试数据集对2个模型进行测试，以验证其性能。测试结果对比如表2所示。

由表2可知，与模型一相比，模型二在在测试数据集上的预测准确率明显更优，且达到了98.8%。

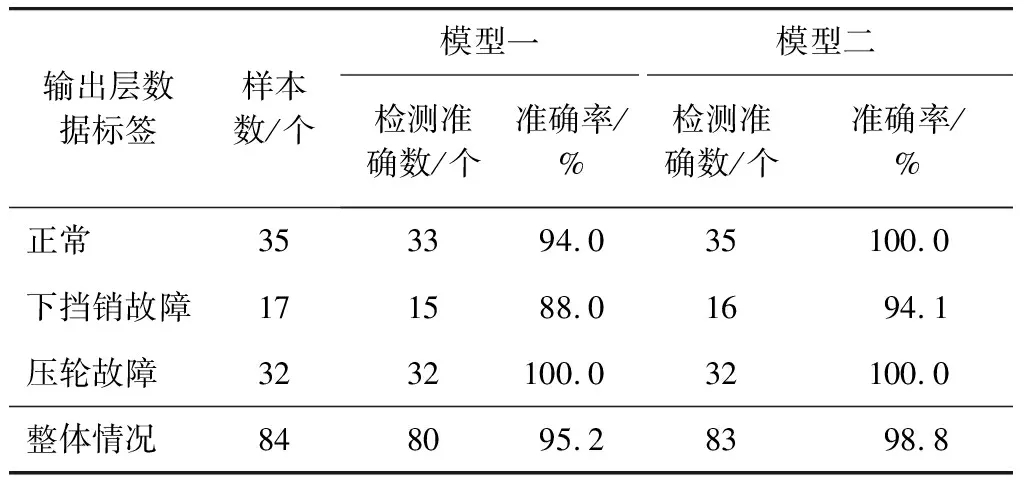
表2 模型一与模型二的测试结果对比

综上所述，利用Dropout法对BP神经网络故障检测模型进行优化，可在一定程度上减少过拟合现象的发生，有效提高故障检测的精度。最终所搭建的BP神经网络故障检测模型能有效地对塞拉门下挡销及压轮故障进行检测，提高了设备运行可靠性。

3 结语

本文通过对不同状态下电机电流信号的时域特征分析，研究对比了不同状态下电机电流信号在时域上的分布差异，建立了一种基于BP神经网络的塞拉门下挡销及压轮故障检测模型。

基于实际案例数据，对该检测模型进行测试分析。测试结果表明：不同状态下的地铁列车塞拉门电机电流信号经预处理后在时域分布上存在着一定差异，通过提取合适的时域特征参数，并结合BP神经网络及Dropout优化技术，能有效检测出塞拉门下挡销及压轮的故障。