高速铁路桥梁墩顶位移对CRTSⅡ型轨道几何状态的影响研究

陈利民 李晓龙 陈 鹤

(上海东华地方铁路开发有限公司, 200070，上海∥第一作者，高级工程师)

上海轨道交通市域线机场联络线(以下简称“机场线”)总长68.68 km，设9座车站。机场线在七宝站南侧部分分为明挖段和隧道段。受通道东侧大量厂房和居民楼限制，部分线路与沪昆高铁线路距离较近。当新建铁路线路与既有高速铁路线路距离较近时，新建铁路线路施工不可避免地会对邻近既有高速铁路线路的下部结构产生影响。

我国现行的规范大多通过测量轨道几何不平顺值来评价高速铁路线路轨道的状态。但是，现有手段无法实时监测轨道几何不平顺值，只能通过监测桥墩墩台等其他结构沉降来对其进行间接测量。由此，准确地计算高速铁路桥墩位移对轨道几何状态的影响并确定其下部结构的位移限值，对于保障既有线路的安全运行具有重要意义。

目前，国内针对高速铁路桥墩位移对高速铁路线路影响的研究多集中在对加速度、减载率等列车行车指标的影响。现有文献[1-6]中多基于列车-轨道-桥梁耦合动力学理论结合有限元仿真分析方法研究桥梁差异性沉降对列车运营加速度及安全性的影响，然而针对桥梁墩顶位移对轨道几何状态的影响较少，罕见提出桥梁墩顶的位移限值。基于此，本文采用有限元分析软件建立桥墩-桥梁-CRTSⅡ型轨道结构模型，研究高速铁路不同桥墩位移下的轨道几何状态变化，为既有高速铁路线路安全性评估提供理论依据。

1 CRTSⅡ型轨道的有限元模型

1.1 轨道结构

CRTSⅡ型轨道为板式无砟轨道，主要包含钢轨、扣件、轨道板、CA砂浆层、底座板、L型挡块等部件，其主要结构示意图如图1所示。

图1 CRTS Ⅱ型轨道结构模型示意图

1.1.1 钢轨

有限元模型中，钢材选用梁单元进行模拟；结合实际情况，选用常见的60 kg/m钢轨，母材为U71Mn(k)，屈服强度取457 MPa。

1.1.2 扣件

采用非线性弹簧单元来模拟扣件，并输入广义的力-变形曲线以定义其非线性行为。为全面考虑扣件系统的纵向阻力、横向刚度和垂向刚度，在钢轨和轨道板上每对应结点之间均分别建立3个弹簧单元来模拟3个方向的扣件刚度。扣件节点按等间距原则布置，桥梁轨道板上的扣件节点间距取629 mm。高速铁路无砟轨道桥梁上常采用WJ-7型小阻力扣件，其位移-阻力关系如图2所示。WJ-7型扣件的最大横向抗力取50 kN，垂向刚度按表1 选取。

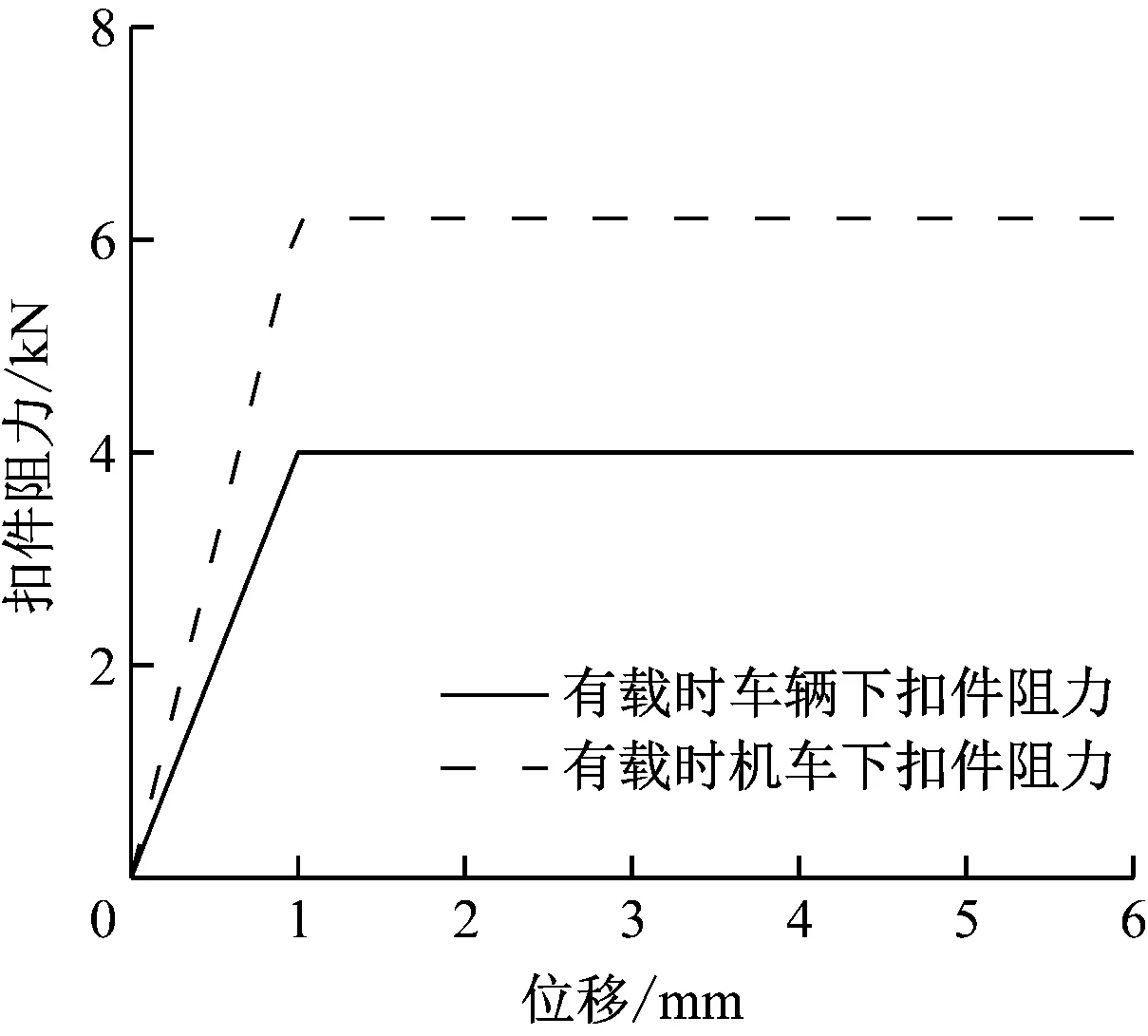
图2 WJ-7型小阻力扣件的位移-阻力关系

表1 WJ-7型扣件垂向刚度

本次模拟轨道板结构为沪昆高铁轨道结构，其为客运专线，因而采用WJ-7B型的垂向刚度。

1.1.3 轨道板、砂浆填充层、底座板

CRTS Ⅱ型轨道为预应力混凝土结构，采用C55混凝土。标准轨道板长度为6 450 mm，宽度为2 550 mm，厚度为200 mm。每块标准轨道板设置10对承轨台，扣件节点间距为650 mm。标准轨道板的实体单元模型如图3所示。

图3 轨道板实体单元模型

砂浆填充层是兼具混凝土刚性和沥青弹性的半刚性体。砂浆材料的28 d抗压强度不低于15 MPa，弹性模量取200 MPa。砂浆填充层采用实体单元进行模拟，与轨道板等长等宽，厚度为30 mm。底座板也采用实体单元模拟，其混凝土强度等级为C35，宽度为2 950 mm，厚度为190 mm。

1.2 桥梁结构

1.2.1 箱梁

箱梁混凝土强度等级为C50。考虑桥梁支座部分截面加厚，箱梁采用变截面实体单元进行模拟，可全面考虑桥梁结构的几何尺寸和材料属性。32 m简支箱梁的实体单元模型如图4所示。本次模拟为分析桥墩变形对钢轨的影响，考虑边界效应的影响，拟建立4跨简支梁(单跨为32 m)进行模拟。

图4 32 m简支箱梁实体单元模型

1.2.2 支座

一般情况下，支座橡胶层自身变形相对桥墩位移极小，可以忽略不计。因此，采用弹簧单元对支座进行模拟。根据支座垂向承载力、水平向承载力与允许位移范围，可计算垂向、横向、纵向刚度，以及转动弹簧刚度，如表2所示。

表2 固定与活动支座各方向模拟弹簧刚度

1.2.3 桥墩

桥墩混凝土强度等级取C30。桥墩同样采用实体单元进行模拟，以便在墩顶面纵横向水平力作用下，计算由墩身弯曲、基础倾斜、基础平移及橡胶支座剪切变形等引起的墩顶位移。

由于本研究主要分析墩顶位移对桥梁上部结构及轨道结构造成的影响，不考虑桥墩自身的变形因素，故而仅取墩顶各方向位移变化工况。

1.3 边界条件

由于有限元模型仅考虑某些桥墩的整体位移对于轨道几何状态的影响，因此除产生位移的桥墩外，剩余桥墩均采用下部固定的边界条件，限制其各方向位移。同时，在沿钢轨方向的轨道板两端，限制轨道板结构的纵向位移。

4跨CRTSⅡ型轨道简支梁桥的有限元计算模型如图5所示。由于施工过程仅影响桥墩的横向及垂向位移，故本研究仅考虑桥墩横向位移工况和垂向位移工况。

图5 4跨CRTSⅡ型板式无砟轨道简支梁桥有限元计算模型示意图

2 轨道几何不平顺的仿真计算

2.1 桥墩横向位移计算工况

4跨简支梁桥3#桥墩整体横向位移dx分别取2 mm、4 mm、6 mm、8 mm、10 mm、15 mm、20 mm、25 mm、30 mm、35 mm、40 mm，通过有限元模型计算轨道几何不平顺值。

单墩dx=40 mm时，轨道几何不平顺值计算结果如图6所示。由图6可知：该工况下，高低不平顺极值为0.643 mm，轨向不平顺极值为2.265 mm，轨距不平顺极值为0.022 mm，水平不平顺极值为0.428 mm，dx对轨向不平顺的影响最大，对其他指标影响较小；当单墩dx=40 mm时，其他不平顺值均小于0.65 mm。

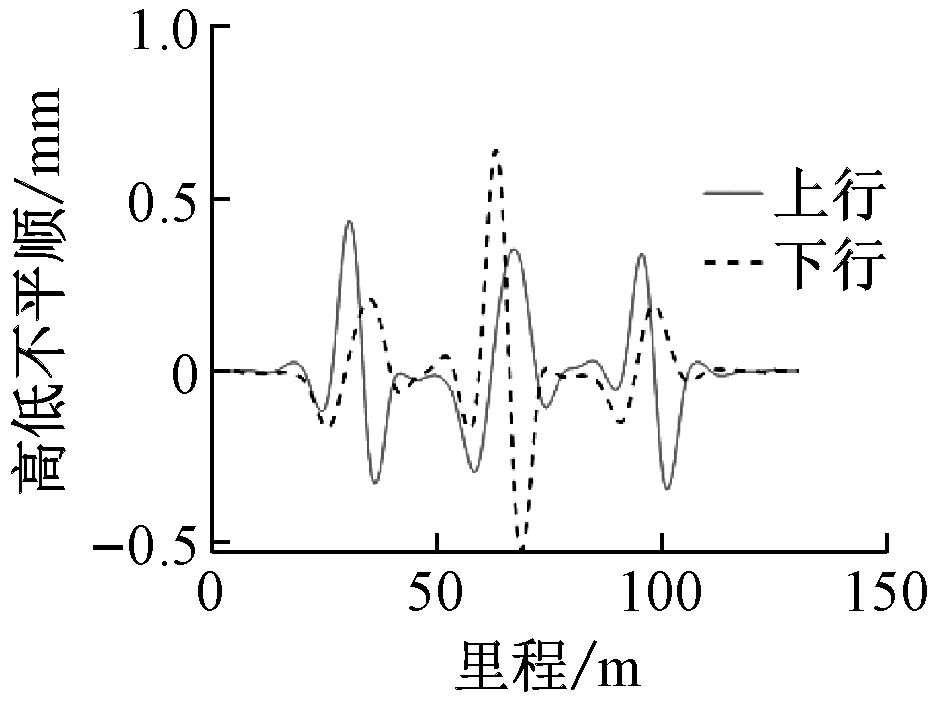
a)高低不平顺

轨向不平顺极值随桥墩横向位移变化如图7所示。由图7可见，轨道轨向不平顺极值与dx基本呈线性关系，拟合公式为dgx=0.056 6dx-0.000 5，拟合优度R2=0.997，其中dgx为轨向不平顺极值，dx为3#桥墩横向位移值。

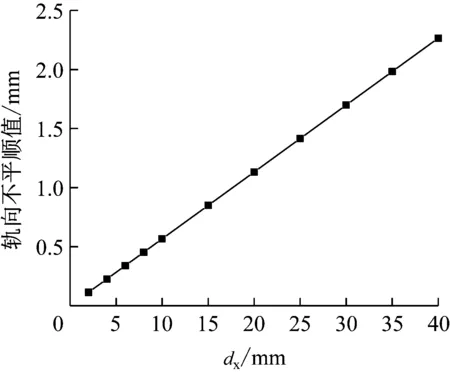
图7 不同dx时的轨向不平顺变化量

2.2 桥墩垂向位移计算工况

4跨简支梁桥3#桥墩整体垂向位移dy分别取2 mm、4 mm、6 mm、8 mm、10 mm、15 mm、20 mm、25mm、30 mm、35 mm、40 mm，通过有限元模型计算轨道几何不平顺值。

单墩dy=40 mm时，轨道几何不平顺值计算结果如图8所示。

由图8可知：高低不平顺极值为5.02 mm，轨向不平顺极值为0.06 mm，轨距不平顺极值为0.03 mm，水平不平顺极值为0.05 mm，桥墩dy对轨道高低不平顺影响较大，对其他指标影响较小；在最不利工况下，其他不平顺值均小于0.07 mm。

2.2 催产及孵化 灰裂腹鱼为一次性产卵，每年2～4月份为其繁殖盛期〔8-9〕。2017年3月10日至3月15日，对成熟度不同的亲鱼分别进行了两批人工催产试验。催产期间，水温平均16℃，效应时间约为70 h左右。见表1。

a)高低不平顺

高低不平顺极值随dy变化情况如图9所示。由图9可以看出，轨道高低不平顺极值与dy基本呈线性关系，拟合公式为dgd=0.124 3dy+0.145 5，R2=0.971，其中dgd为高低不平顺极值，dy为3#桥墩垂向位移值。

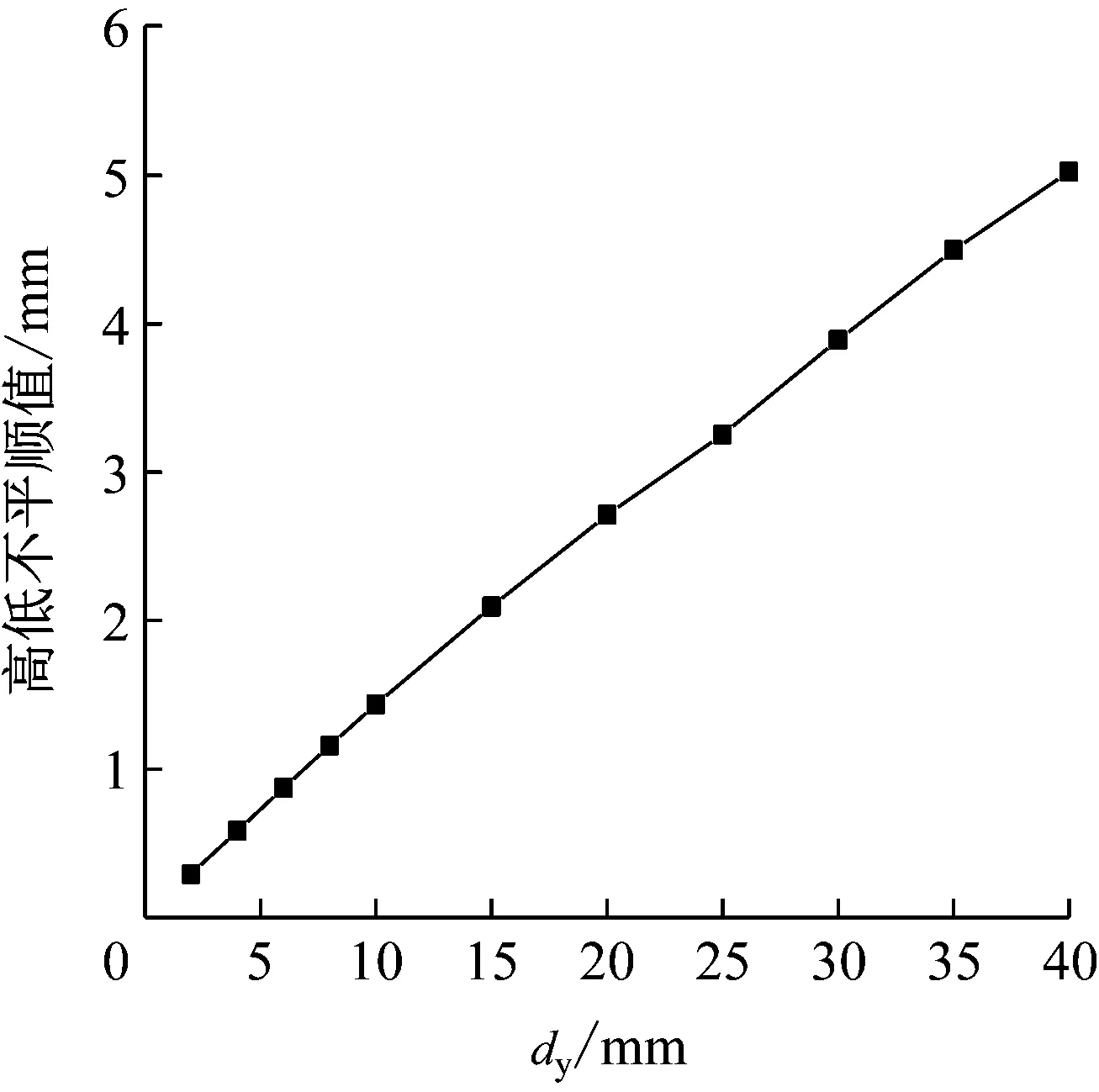
图9 不同dy时的高低不平顺值变化量

2.3 桥墩双向位移计算工况

在双向位移计算工况中，取4跨简支梁桥3#桥墩整体同时发生横向位移dx和垂向位移dy。按双向位移(即dx与dy同时发生相同位移量d双)d双分别取2 mm、4 mm、6 mm、8 mm、10 mm、15 mm、20 mm、25 mm、30 mm、35 mm、40 mm，通过有限元模型计算轨道几何不平顺值。

单墩d双=40 mm时，轨道几何不平顺值计算结果如图10所示。由图10可见：高低不平顺极值为5.08 mm，轨向不平顺极值为2.52 mm，轨距不平顺极值为0.09 mm，水平不平顺极值为0.44 mm，单个桥墩双向位移对轨道高低不平顺和轨向不平顺影响较大，对其他指标影响较小；且与单个桥墩单向位移相比，单个桥墩双向位移的高低不平顺和轨向不平顺值均有小幅度的增加。

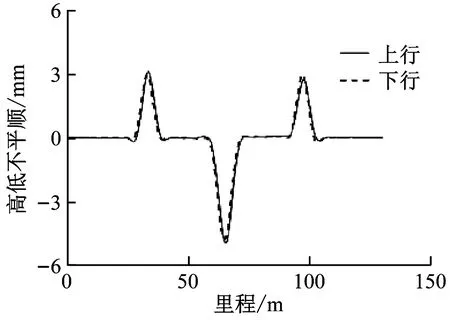
a)高低不平顺

最大轨向不平顺值和高低不平顺值随桥墩d双变化如图11所示。由图11可以看出：在单墩双向位移计算工况下，轨道高低不平顺极值与双向位移量基本呈线性关系，拟合公式为dgd=0.125 8d双+0.146，R2=0.947，其中dgd为高低不平顺极值，d双为3#桥墩双向位移值；在单墩双向位移工况下，轨道轨向不平顺极值与双向位移量基本上呈线性关系，拟合公式为dgx=0.062 9d双+0.018 5，R2=0.972，其中dgx为轨向不平顺极值，d双为3#桥墩双向位移值。

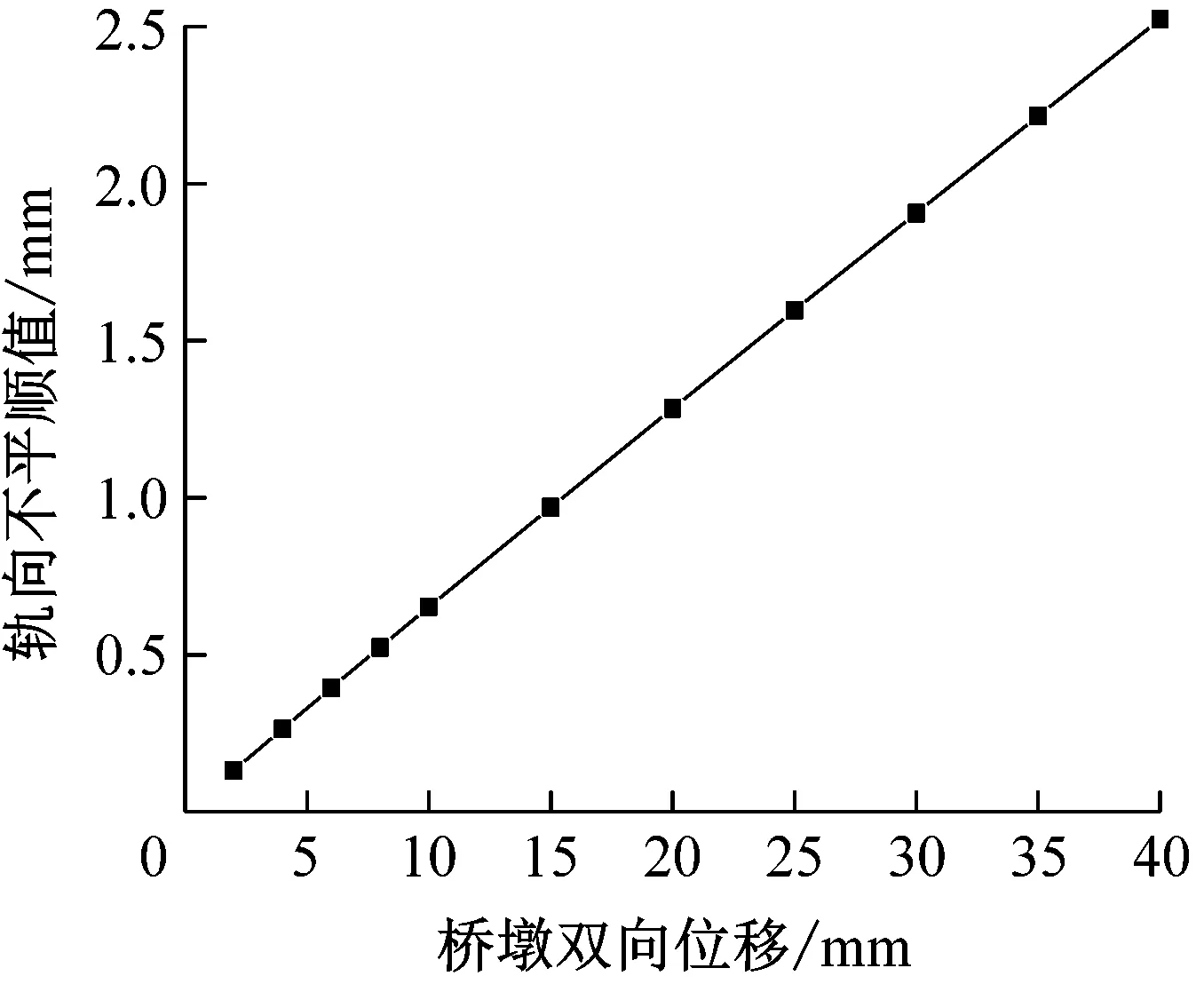
a)轨向不平顺

3 桥墩位移限值的建议值

根据轨道几何不平顺的计算结果，桥墩的位移与相应轨道不平顺极值存在线形关系。本文根据目前现有规范，并按结构应力水平不能超出其强度的要求，给出桥墩位移限值的建议值。

首先，根据《普速铁路线路修理规则》中对于静态轨道几何状态不平顺的规定，将作业验收的不平顺值4.000 mm作为线路轨道的初始不平顺；然后，叠加不同计算工况下的几何不平顺极值计算值，得到几何不平顺值限值的参考值；最后，综合考虑结构应力情况，提出单墩位移限值建议值。

3.1 单墩横向位移限值建议值

单墩横向位移40 mm工况下，轨向不平顺值为6.265 mm(即4.000 mm +2.265 mm)，大于计划修补限值6.000 mm，小于临时修补限值12.000 mm。根据仿真结果，此时的底座板最大拉应力已超限。因此，轨向不平顺不作为桥墩横向位移限值的指标。

3.2 单墩垂向位移限值建议值

在dy=15 mm工况下，高低不平顺值为6.094 mm(即4.000 mm+2.094 mm)，超过计划维修限值6.000 mm。故垂向位移限值应控制在15 mm以内。此外，桥墩垂向位移过大会引起轨道板脱空，进而对列车的安全运行造成影响。由此，考虑一定的安全储备，单墩垂向位移控制建议值取12.0 mm。

3.3 单墩双向位移限值建议值

由于双向位移会加剧轨道不平顺极值，所以双向位移限值应对单墩单向位移限值进行折减。考虑一定的安全储备，双向位移控制建议值为7.2 mm。

4 结论

1)单墩横向位移、单墩垂向位移以及单墩双向位移分别为2 mm、4 mm、6 mm、8 mm、10 mm、15 mm、20 mm、25 mm、30 mm、35 mm、40 mm计算工况下，钢轨变形随着桥墩位移的变化而变化。

2)桥墩横向位移主要对轨道轨向不平顺产生较大影响，且轨向不平顺极值与桥墩横向位移呈线性关系；横向位移为40 mm时，轨向不平顺极值为3.299 mm，其他不平顺极值均小于1 mm。桥墩垂向位移对轨道高低不平顺产生较大影响，且高低不平顺极值与桥墩垂向位移呈线性关系；垂向位移为40 mm时，高低不平顺值为8.693 mm，其他不平顺值均小于0.1 mm。

3)综合考虑《普速铁路线路修理规则》的相关要求、结构应力水平、钢轨几何不平顺值维修准则等，建议桥墩位移限值：单墩垂向位移限值为12.0 mm，单墩横向位移限值为9.0 mm，单墩双向位移限值为7.2 mm。