地震动输入界面的选取对地铁车站地震反应的影响

何 荆，殷 琳，蔡海兵，舒 恩

(1.安徽理工大学 土木建筑学院，安徽 淮南 232001；2.宁波工程学院 建筑与交通工程学院，浙江 宁波 315000)

近年来，关于结构抗震性能的研究取得了广泛关注[1-2]。研究地铁车站结构地震反应规律时，常采用基于有限元建模的时程分析法。建模时，需在半无限空间中截取有限范围土体，其中底部边界的选取问题也应关注[3]。关于地下结构有限元分析模型的底部边界问题，国家相关规范[4]给出建议：底部边界应从距地下结构距离3倍结构单边最大尺寸处至基岩面，该建议给出底边界取值的范围较宽，可操作性不强。为此，上海市规范[5]在此基础上建议底部边界取至地表向下70m处。上海地区软土层厚度普遍在200m以上，按上海市规范建议，计算模型土层厚度约取为实际土层总厚度的1/3，如此将导致计算模型的动力特性与实际情况有较大差别，因此可能会导致一定的计算误差，关于误差变化情况目前少有研究。基于此，本文以上海典型深厚软弱场地地铁车站作为算例，分析底部边界选取不同对地铁车站地震响应影响。

1 基本运动方程及求解

对地下结构-土层系统建立运动方程时，可采用粘滞阻尼或复数阻尼。当采用粘滞阻尼时，土层-地下结构进行地震反应计算的运动方程如式(1)所示。

(1)

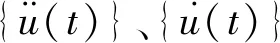
对式(1)的求解，可选用模态叠加法或逐步积分法。当计算系统为土层-地下结构这种基频低、模态密集、自由度规模大的系统时，不适合用模态叠加法，因为这类计算系统需要较多的模态参与才能得到精度满意的计算结果，不方便计算。若选用逐步积分，又会因阻尼矩阵的构造带来计算误差[6]。

采用复数阻尼可以避免粘滞阻尼带来的问题。采用复数阻尼时，土层-地下结构进行地震反应计算的运动方程如式(2)所示。

(2)

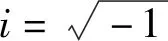
(-ω2[M]+2iη[K]+[K]){u(ω)}={peff(ω)}

(3)

在复数域内求出{u(ω)}，如式(4)所示。

(4)

若计算系统由多种不同阻尼比的材料组成，还可以将式(4)变形为式(5)。

(5)

其中，ηj为第j种材料滞后阻尼系数，[Kj]为第j种材料的刚度矩阵。

将式(4)作Fourier逆变换可得时域内位移的解{u(t)}。由式(4)可知，相比于采用粘滞阻尼，采用复数阻尼的优点如下：①仅需求解复代数方程，对计算机硬件要求不高；②阻尼比不随激振频率的变化而变化，不会因阻尼矩阵的构造带来误差；③对不同的材料可以设置不同的阻尼比，不需要对系统的阻尼比进行等效。复数阻尼的不足之处在于对非线性问题，只能进行等效线性计算，不方便进行真非线性分析。

2 算例

本文选取2个不同场地条件下的地铁车站为算例。研究不同地震动输入对地铁车站地震反应的影响。算例1为上海市人民广场场地中的典型地铁车站结构，不考虑土体的非线性性质。算例2为上海市轨道交通13号线某站点场地条件下的地铁车站结构，土体非线性采用等效线性化计算。

算例1：上海市人民广场场地土层深约230m，共有18层土，各层土物理性质如表1所示。地铁车站埋深2m，为双层双柱岛式钢筋混凝土结构。车站断面总宽为20m，高11.54m，中跨宽6m，侧跨宽6.3m，上层高3.5m，下层高6.4m，中柱间距7.8m。顶板、底板、侧墙弹性模量为3.0×1010pa，密度为2.5×103kg/m3。因中柱具有不连续性，采用二维平面应变模型时，应将中柱材料参数进行等效[7-9]。等效后中柱弹性模量为3.08×109pa，密度为3.2×102kg/m3。建立阻尼模型时，整个计算模型的阻尼比近似取为0.05[10]。地铁车站横截面形式如图1所示。

表1 算例1场地土性质物理参数

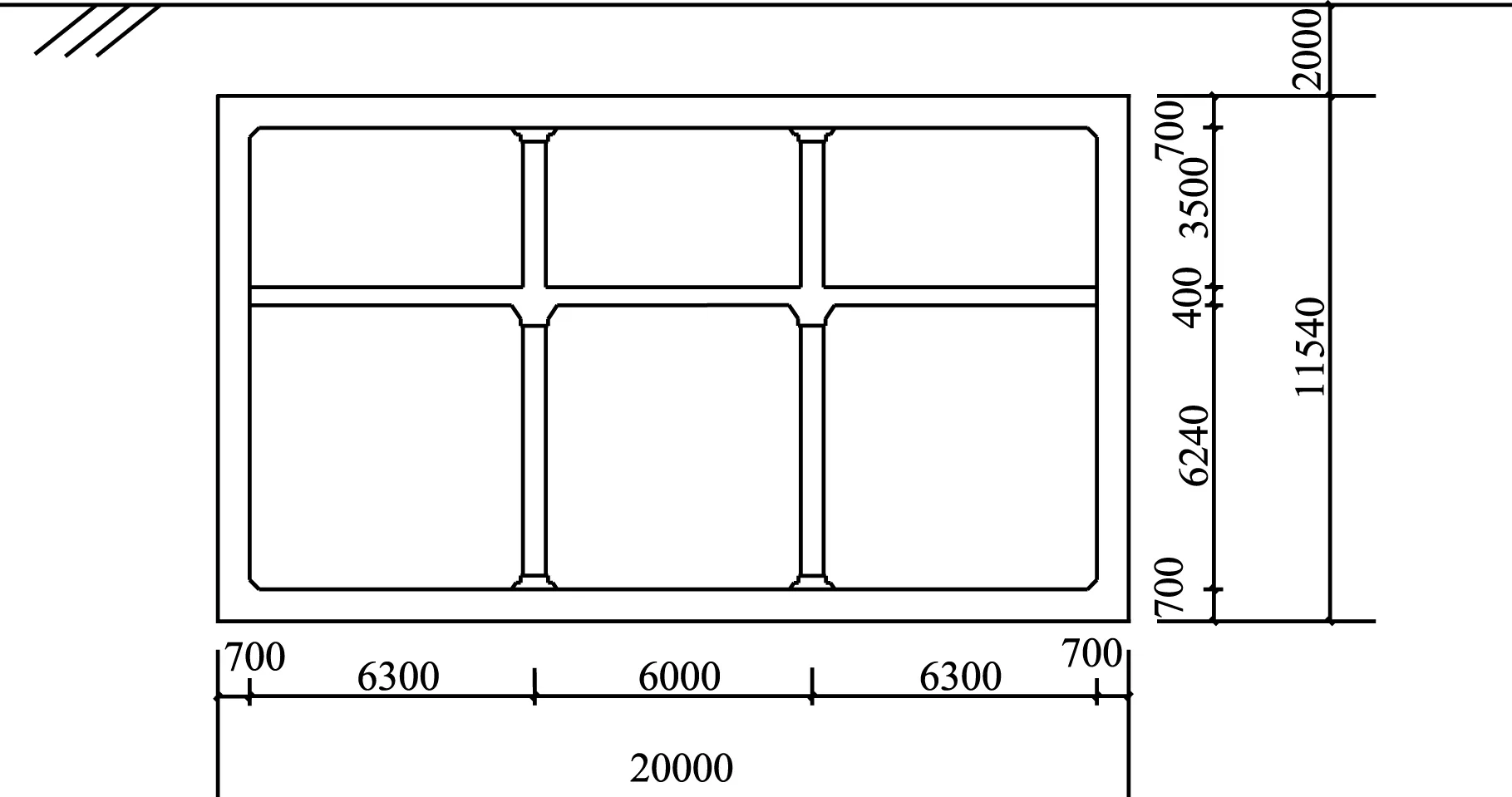
图1 地铁车站截面图

采用二维平面应变模型时，为减少侧向边界带来的计算误差，根据楼梦麟等人[11]研究计算模型的水平向宽度取1150m。土体部分用四边形等参元进行离散，单元竖向网格尺寸控制依据为25Hz正弦波所对应波长的1/16～1/8，横向网格尺寸取为竖向的2～3倍。约束土体侧边竖向自由度，放松水平向自由度，使之成为侧移边界。约束模型底部结点所有自由度，使其成为固定边界。地下结构用梁单元离散，不考虑土体与地下结构间的脱离与滑移。

采用三种地震波作为激励地震动，即汶川波、Kobe波、人工波1。其加速度时程及其FFT谱如图2所示。

(a1)汶川波时程图(a2)Kobe波时程图(a3)人工波1时程图(b1)汶川波FFT谱(b2)Kobe波FFT谱(b3)人工波1FFT谱图2 算例1地震波时程及其FFT谱

为评价不同地震动输入面对地铁车站结构地震反应的影响，建立两个计算模型。模型1的地震动输入面取至基岩面处，称之为界面1，以汶川波、kobe波、人工波1作为激励地震动，相应工况为1a；模型2地震动输入面为离地表70m处的假设基岩面，本文称之为界面2，以处理后的汶川波、kobe波、人工波1作为激励地震动，工况称之为1b。模型1和模型2的计算简图如图3所示。

(a)模型1(b)模型2图3 算例1两种输入界面模型计算简图

大量震害结果表明[12-13]地下结构中柱顶、中柱底、侧壁顶、侧壁底是薄弱环节，故提取这四个部位在最不利情况下的内力进行分析，其内力峰值情况如表2所示。

表2 算例1地下结构地震反应峰值

由表2可知，算例1a、1b在三种不同地震波激励下，侧壁的剪力、弯矩、轴力值均大于中柱，算例1a四个部位相应内力均小于算例1b。其中，汶川波激励下，地铁车站四个部位的内力明显大于其他两个地震波，侧壁底的最大弯矩值更是达到了1235.20kN·m。为充分分析模拟时基岩面选取不同对计算结果的影响，利用误差计算公式(6)。

η=100%×(Rb-Ra)/Ra

(6)

分别计算算例1中工况1a和工况1b的误差值，对相应误差值进行分析。式(6)中Ra为1a对应内力值，Rb为1b内力值，误差情况如图4所示。

(a1)算例1弯矩误差图(a2)算例1剪力误差图(a3)算例1轴力误差图图4 算例1误差变化图

由图4可知，在人工波1和Kobe波激励下，四个部位误差变化情况类似。除侧壁顶轴力误差略小于侧壁底外，其余顶部内力误差均大于底部。与人工波1相比，Kobe波四个部位的弯矩、剪力误差值比较接近，都在58%左右。汶川波激励下，误差变化情况与Kobe波和人工波1不同。汶川波激励下，顶部弯矩、剪力、轴力误差均小于底部，其中侧壁底剪力误差高达61.41%，相较侧壁顶增长近31%。综合来看，算例1在不同波的激励下，误差值均值为正，内力误差范围在16.79%～61.75%。

算例2：上海轨道交通13号线某车站场地土层厚327.6m，分18层土，各层土的厚度和物理性质如表3所示，各层土的非线性性质如表4所示。该车站结构尺寸和材料物理性质与算例1一致。本算例的模型计算范围、有限单元的选择、网格尺寸的确定，边界条件的设置均与算例1相一致。

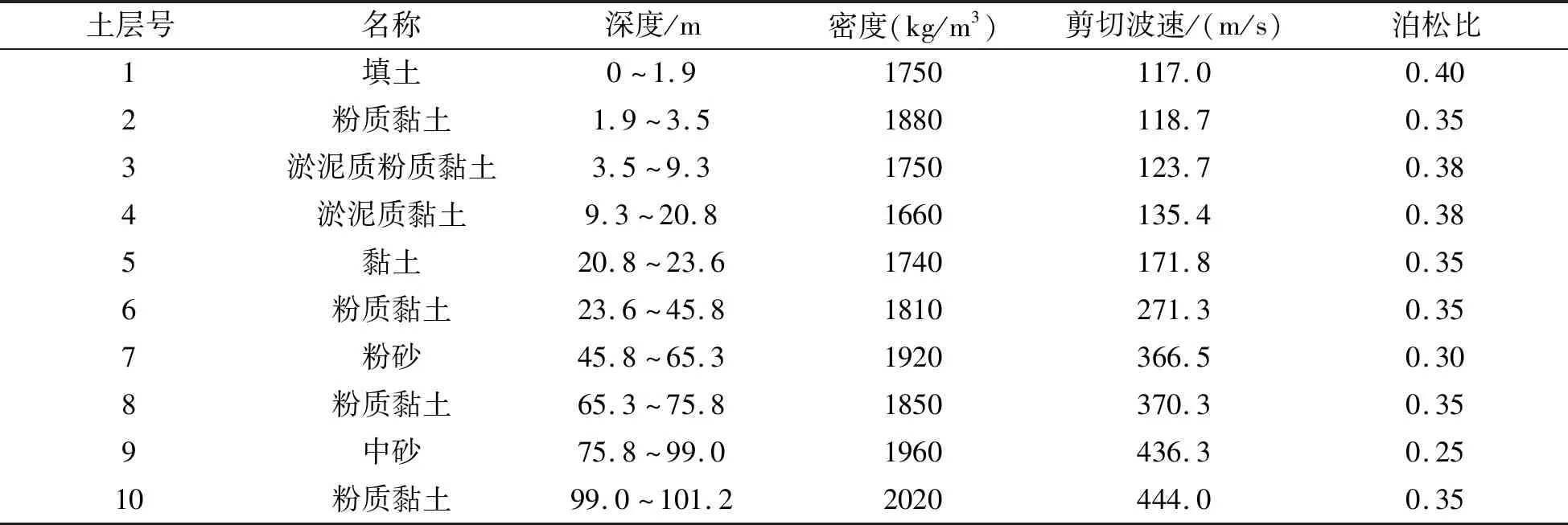
表3 算例2场地土性质物理参数

续表3

表4 土体动剪切模量和阻尼比值

算例2采用安评资料生成的人工波2作为激励地震动，其加速度时程及其FFT谱如图5所示。

(a)人工波2时程图

建立2个计算模型，模型1的地震动输入面为离地表327.6m的真实基岩面处，以人工波2作为激励地震动，相应的工况称之为2a；模型2的地震动输入面取为离地表70m处的假设基岩面，以处理后的人工波2作为激励地震动，相应的工况称之为工况2b。模型1和模型2的计算简图如图6所示。

(a)模型1(b)模型2图6 算例2两种模型计算简图

中柱顶、中柱底、侧壁顶、侧壁底内力峰值情况如表5所示。利用误差计算公式(6)，计算算例2误差值，对其误差值进行分析。其中，Ra为2a对应内力值Rb为2b内力值，误差情况如表5所示。

表5 算例2地下结构地震反应峰值和误差

由表5可得，在人工波2的激励下，中柱顶弯矩、剪力均大于中柱底，轴力略小于中柱底。侧壁顶各个内力均小于侧壁底。算例2b四个部位的内力值都大于算例2a。弯矩、剪力、轴力误差变化情况与算例1中汶川波激励时相似，顶部误差小于底部误差，误差值在29.19%～61.41%之间。

3 结论

(1)地铁车站基岩边界取至地表往下70m处，各重要部位内力均大于取至实际基岩面深度，会产生较大误差。故有限元模拟时应选用真实基岩面作为地震动输入面。

(2)不同地震波激励下，基岩边界取至地表往下70m左右处与取至实际基岩面处相比，产生误差大小不同。其中Kobe波激励下产生误差最大，各重要部位误差大小也较为集中，均在58%～62%之间。

(3)在汶川波和人工波2激励下，中柱顶、侧壁顶的弯矩、剪力、轴力分别小于中柱底、侧壁底。在人工波1和Kobe波激励下，除侧壁顶轴力小于侧壁底外，中柱顶和侧壁顶的弯矩、剪力均大于中柱底和侧壁底。