中国养老服务床位数的预测与分析

唐鹏翔，张晓美

（吉林医药学院药学院，吉林 132013）

0 引言

中国是世界上人口最多的发展中国家，随着老龄化进程加速，养老服务问题日益突出，增加养老服务床位是一个亟待解决的现实问题，参考中国统计局官网［1］、中国民政部公报［2］等相关数据，利用数学模型，对未来养老服务床位数量进行合理预测，有较强的现实意义。通过预测结果进行综合研判，可以对未来养老工作的开展提供便利，更好地服务国家战略，为将来中国老龄化问题提供一条解决思路。

谭英花在《上海机构养老资源配置研究》［3］中利用曲线参数估计模型和年龄模型对养老资源进行预测，从微观和宏观两个层面构建资源的评价体系。徐宗煌［4］在《基于多元回归模型的养老床位需求预测》中利用Leslie 矩阵模型、BP神经网络预测养老床位数量情况。王子鑫等［5］在《养老服务床位需求预测与运营模式模型分析》中使用多元线性回归模型和Dijkstra 算法解决了养老床位需求问题。

本文通过中国统计局官网和民政部公报提供的数据，建立养老服务床位数的logistic 模型、ARMA 模型，使用MATLAB 和Eviews 两种软件计算得到我国未来养老服务床位数；另外建立养老服务床位数与养老人口数比例的数学模型，65 岁以上的老年人口的指数模型也可以得到未来我国养老服务床位数的变化情况，并对这三种预测结果进行对比分析。

1 数据来源

本文所使用的养老服务床位数来自中华人民共和国民政部2006年后的年度统计公报。65岁以上老年人口数来源于中国统计局官网统计数据。

2 模型的建立与计算

2.1 模型1：养老服务床位数的logistic模型

根据民政部公布的养老服务床位数统计情况（见表1），使用MATLAB 对表1 数据绘制散点图（以2006年为初始时刻0），结果如图1所示。

表1 民政部公布的养老服务床位数统计情况万张

图1 养老服务床位数变化情况散点图

从已有数据的散点图分析可知，养老服务床位数在增加，但是增加幅度在逐渐减缓。从趋势上看，符合“S”型曲线趋势［6］。从机理上分析老年人养老服务床位数量变化，由中国民政部每年年度公报中发布的养老服务床位数可知，养老服务床位数虽然在不断增加，但是由于建设资源、选择意愿等因素对老年人养老服务床位数增长起到了阻滞作用，并且随着时间的推移，阻滞作用越来越大。因此，对养老服务床位数设立阻滞增长模型（Logistic模型）。

设第t年的养老服务床位数为x(t)，年增长率为r，初始养老服务床位数为x0，则x(t)满足的微分方程是：

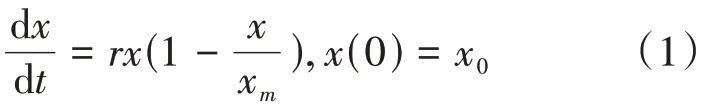
其中xm为最大养老服务床位数。其解为

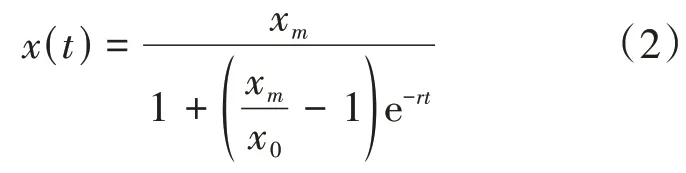
使用MATLAB 曲线拟合工具箱cftool 进行参数拟合［7］，计算时床位数以百万为单位，得出图2。

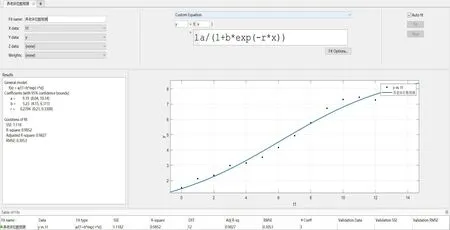
图2 基于MATLAB养老服务床位拟合结果

计算得xm=9.19，r= 0.2704，拟合优度为0.9827，残差值为1.118，拟合效果较好，故养老服务床位数预测的logistic模型为

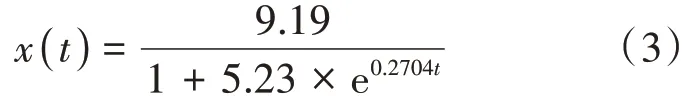
得到养老服务床位数的预测模型后，利用模型计算相关已知年份的床位数据并与已知数据进行对比，发现模型计算结果与已知数据相差较小（见表2）。

表2 模型结果与实际比较万张

最后，使用养老服务床位数模型进行计算，获得未来30年（2020—2050）的数据如表3所示。

表3 未来30年养老服务床位数据结果万张

利用已知和计算后的数据作图（见图3），展示后可以看出，养老服务床位数据图像呈“S”曲线，较符合阻滞增长模型［8］情况，具有良好的预测意义。

图3 logistic模型预测结果图

通过所建立的logistic 模型计算结果可得，我国养老服务床位数将逐年稳定至919.0万张。

2.2 模型2：养老服务床位数的自回归移动平均模型

2.2.1 时间序列自回归移动平均模型

将养老服务床位数视为一个时间序列{Xt}，可以记为ARMA(p,q)。其中ARMA(p,q)模型［9］的数学表达式可表示为

其中，φ1,…,φp为自回归系数，θ1,…,θq为移动平均系数。

2.2.2 数据的平稳性检验

将2006—2020 年养老服务床位数的数据输入到Eviews 软件中，对该数据进行时间序列的预处理［10］，首先得到图4 的时序图，该时序图中的数据呈递增趋势，该图趋势性明显，而对于平稳序列的要求是时序图应该要在一个值附近上下波动，所以通过对该时序图的观察，该序列不是平稳序列［11］。

图4 养老服务床位数的时序图

对于不平稳序列，可以使用差分使其平稳化［12］，首先采用一阶差分的方法，将数据在Eviews 软件下通过一阶差分得到新序列，然后对其进行平稳性检验。

图5 养老服务床位数序列的时序图（一阶差分后）

进行单位根检验［13］，运用Eviews 软件得到的结果见表4。

表4 一阶差分后的单位根检验结果

通过对表4 的结果分析，ADF 检验中t 统计量为-2.300073，与1%、5%、10%的t 统计量比较，其更大，则应该接受该序列存在单位根的原假设，所以与上面时序图检验结果相同，认为该序列是不平稳的［14］，再将养老服务床位数进行二次差分处理，结果如图6所示。

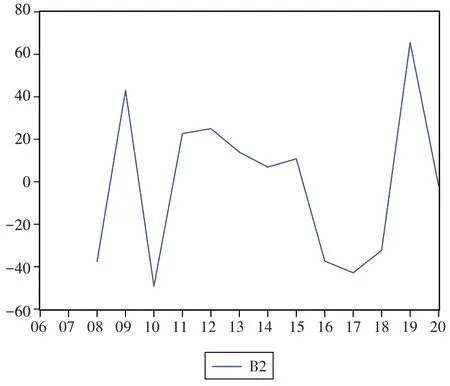
图6 养老服务床位数序列的时序图（二阶差分后）

再次进行单位根检验，结果见表5。

表5 二阶差分后的单位根检验结果

t统计量相应的概率值P=0.0097，非常小，则应该拒绝该序列存在单位根的原假设，认为该序列是平稳的［15］。

2.2.3 ARMA模型的识别

养老服务床位数的ARMA 模型识别即识别模型的阶数( )p,q，通常借助序列的相关图。

根据得出的自相关和偏自相关图（见图7），目前预测该模型可为ARMA( 1,1) ，ARMA( 2,2 ),ARMA( 4,4 )等。但是具体选择哪个模型，还需要综合考虑不同模型的各项指标，通过对比选择最优的一个模型来进行拟合。

图7 二阶差分后的自相关和偏自相关图

2.2.4 ARMA模型的选择

用Eviews 软件建立ARMA 模型后，需要对模型进行对比分析，然后选择一个最优模型，以下所给出的两个模型是经过初步对比后效果相对较好的模型，下面就对这两个模型进行对比分析选最优。

通过图8 可以看到，参数的t统计量p值都小于0.05，说明模型中的参数估计显著非零；决定系数和调整后的决定系数（即R- squared和AdjustedR- squared）分 别 约 为0.820 和0.803；AIC和SBC的 值（即Akaike info criterion 和Schwarz criterion）分别约为8.535和8.167；DW值（即Durbin-Watson stat）约 为1.396［16］。模 型ARMA( )

图8 建立ARMA（1,2,1）模型结果

1,2,1 的拟合效果非常好，但是我们要看有没有比它更好的模型。

通过图9 可知，参数的t统计量p值都小于0.05，说明模型中的参数估计显著非零；决定系数和调整后的决定系数（即R- squared 和AdjustedR- squared）分 别 约 为0.470 和0.412；AIC和SBC的值分别约为9.599，9.672；DW值（即Durbin-Watson stat）约为1.436。由此可以对比两个模型的各项指标，结果见表6。

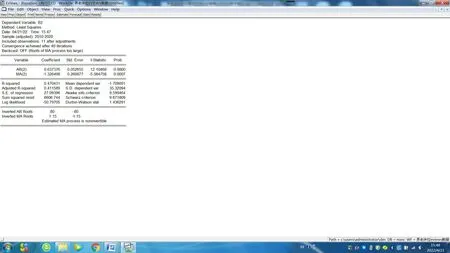
图9 建立ARMA（2，2，2）模型结果

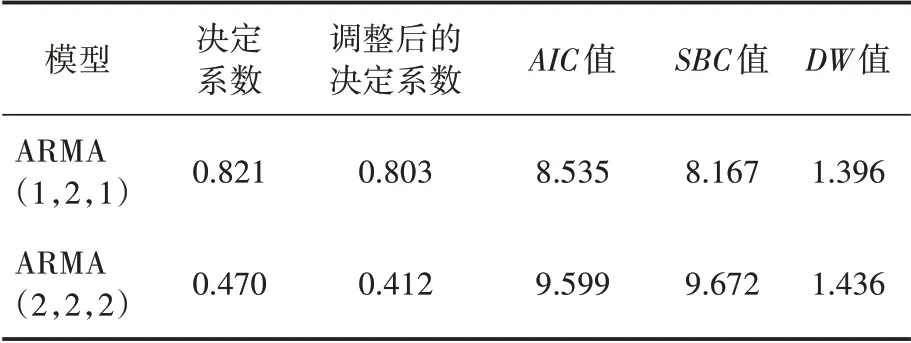
表6 模型指标对比结果

由以上五个指标的对比可以看出，相比之下，ARMA（1，2，1）模型的决定系数较大，AIC值、SBC值两模型差别不大［17］。因此，按照简单性原则，选择ARMA（1，2，1）模型，对拟合模型的残差序列做纯随机检验，对ARMA（1，2，1）模型进行残差序列相关性检验结果如图10 所示。

通过图10，可以得到残差为纯随机序列，残差值较小，选用模型较为恰当。因此，可以得到预测模型公式（数据经过二阶微分处理）：

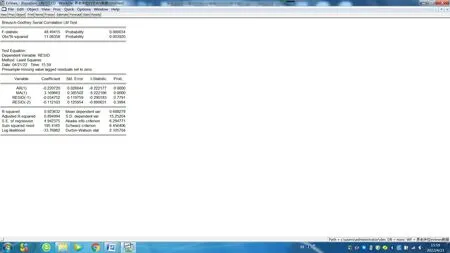
图10 ARIMA（1，2，1）模型相关性检验

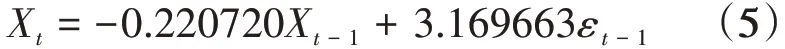
绘制预测图，结果如图11和图12所示。

图11 模型拟合效果图

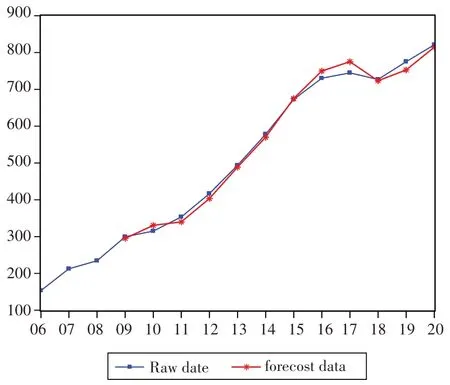
图12 模型预测图

从图11 和图12 可以看出，模型预测效果较好［18］。于是计算模型预测结果，见表7。

表7 ARIMA（1，2，1）模型预测结果万张

2.3 模型3：养老服务床位数与65岁以上老年人口数比例的logistic模型

利用已知的中国民政部官网每年公布的养老服务床位数和中国统计局65 岁以上老年人口数据，计算床位数与养老人口数比例，结果见表8。

表8 养老服务床位数与养老人口数比例%

以时间为横坐标，床位数与老龄人口的比值为纵坐标，绘制散点图，如图13所示。

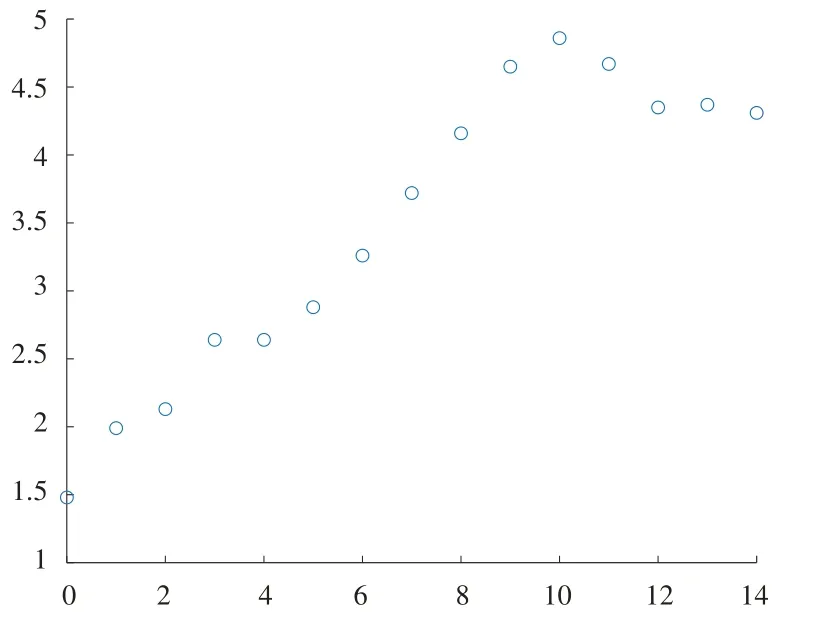
图13 养老服务床位数与养老人口数比例散点图

图13 中散点随着时间的推移，增长趋势受到阻滞且最终较平稳，与logistics 模型曲线较为相似。利用MATLAB 对时间和每年床位数与老龄人口的比值进行曲线拟合［19］。利用已知的人口阻滞增长模型（logistics 模型）来预测养老服务床位数与养老人口数比例，结果如图14所示。

图14 床位数与养老人口数比例拟合结果

通过曲线拟合得到：

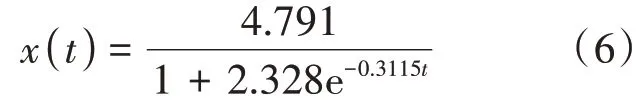
模型显示残差值SSE=1.055，拟合优度R=0.939，拟合结果较好。

模型计算结果数据，见表9。

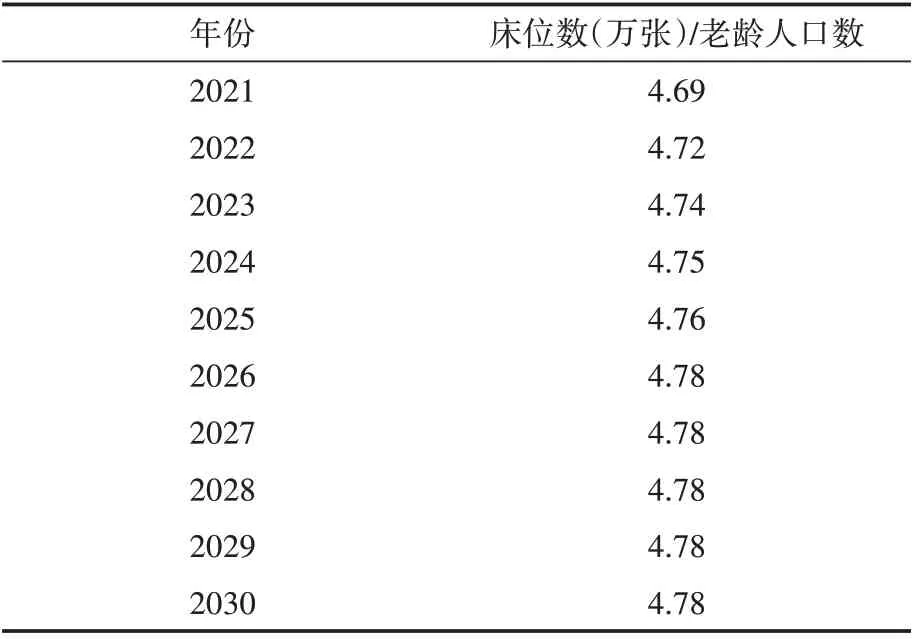
表9 未来养老服务床位数与养老人口数比例%

通过拟合结果可以发现，未来随着时间推移，床位数与养老人口数比例逐渐趋于4.78%附近，但是65 岁以上老年人口数还在增长，说明65 岁以上老年人对于养老机构养老的选择只有微小增长，比例较稳定。

通过模型结果发现，我国65 岁以上老年人对选择养老服务床位的意愿还处于较低水平。造成这一现象可能有多种原因，如家庭状况等［20］。在我国65 岁以上老年人口持续增长的背景下，我国应加快养老机构的建设、完善相关政策等［21］，养老机构应当加强对于养老的研究与探索，找到符合我国或某地区的合理养老规划方案，使更多65 岁以上老年人到养老机构养老，减缓社会相关养老压力［22］。

2.4 模型4：65岁以上老年人口的人口指数模型

二百多年前，英国人口学家马尔萨斯（Malthus，1766—1834）调查了英国一百多年的人口统计资料，得出了人口增长率不变的假设，并据此建立了著名的人口指数增长模型［23］，本文利用此模型进行未来65岁老年人口数的短期预测。

设t年后65岁以上人口数为x(t)，年增长率为r，初始人口数为x0，则x(t)满足的微分方程是：

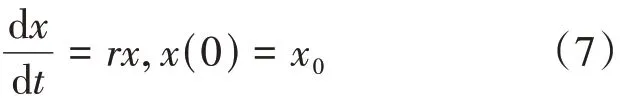
其解为：

根据中国统计局官网数据，得到我国65 岁以上人口数据，见表10。

年份65岁以上人口数年份65岁以上人口数1990 6368 2006 10384 1991 6938 2007 10702 1992 7218 2008 11023 1993 7289 2009 11343 1994 7622 2010 11934 1995 7510 2011 12277 1996 7845 2012 12777 1997 8085 2013 13262 1998 8359 2014 13902 1999 8679 2015 14476 2000 8821 2016 15037 2001 9062 2017 15961 2002 9377 2018 16724 2003 9692 2019 17725 2004 9879 2020 19059 2005 10068

相关数据绘制成散点图（图15），发现我国65 岁以上老年人口从1990 年—2020 年大概呈指数函数型增长。

图15 我国65岁以上老年人口散点图

使用MATLAB 曲线拟合工具箱cftool，进行参数x0,r的计算，以1990 年为初始年份，其对应的t值为0，拟合结果如图16所示。

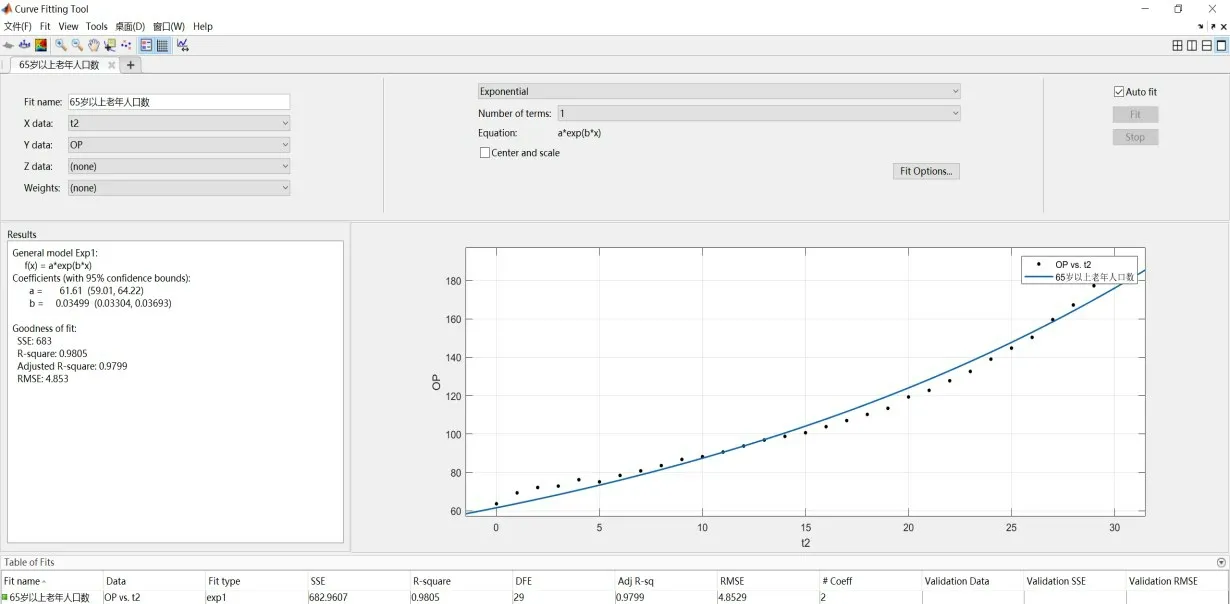
图16 65岁以上老年人口指数模型拟合图

计算得x0= 61.61,r= 0.03499，拟合优度为0.9805，拟合效果较好，故65 岁以上人口的预测模型为

根据模型4，绘制出拟合效果图和至2030年65岁以上人口数的预测曲线，结果如图17所示。

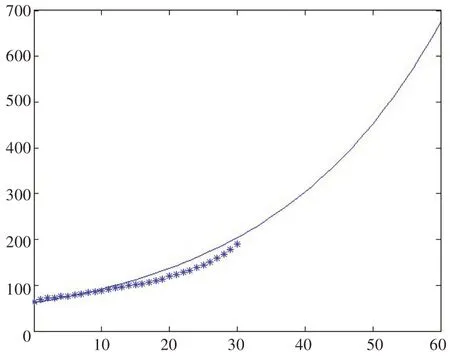
图17 65岁以上人口拟合图预测图

从预测值看，到2050 年我国老年人口将达到7亿，这与实际情况有一定差距，主要是各种因素影响使人口增长率为常数的假设不成立［24］。但是我国老年人口数实际上还在增加，此人口指数模型进行短期预测能起到一定参考作用。

3 模型比较与分析

根据上海养老网站整理得到民政部2021 年公布养老服务床位数，用于不同模型间比较，结果见表11。

表11 模型预测比较万张

通过表11可知，三个模型预测结果中logistic模型与ARIMR（1，2，1）模型预测效果相似且较好，指数模型预测得到65 岁以上老年人口数，再乘以床位数与养老人口数比例得到养老服务床位数预测误差稍大。但是随着未来各种未知因素影响（如：生育政策等），利用该方法进行预测能及时调整，更加动态灵活，也具备一定的预测价值。

4 结语

本文使用两种软件建立四种数学模型预测养老服务床位数、床位数与65 岁以上老年人口比例、65 岁以上老年人口数。目前2021 年养老服务床位数仅为821 万张。模型1 计算结果显示2030 年我国养老服务床位为911.8 万张；模型2计算结果显示为1121.682 万张，还有较大的提升空间；模型3预测结果显示，未来养老服务床位与65岁以上老年人口数比例继续呈上升趋势，但上升空间较小，在2026 年将逐年稳定至4.78%；模型4预测结果显示未来65岁以上老年人口数还会继续增加。

从模型比较和应用来看，根据历史养老服务床位数建立模型1 和模型2，基于当前影响因素条件下进行的预测。如果未来出现新的影响因素（如新生育政策等），则需要重新计算模型系数，从而保持模型预测的准确性。模型3计算比例显示，我国65 岁以上老年选择养老服务床位的意愿处于较低水平，面对日益增加的老龄人口，可以改善养老服务模式，提升养老服务机构建设等，从而增加老年人选择养老服务床位的比例［25］。而模型3 和模型4 可以结合使用，当未来65 岁以上老年人口数或者65 岁以上老年人选择养老方式的意愿发生较大变化时，调整其中一个模型进行计算就能得到预测结果。更加简便快捷，能更加适应短期内的动态变化调整，短期内时效性更强。总的来说，本文核心研究内容是养老服务床位的需求预测，四个模型各有特点，能适应长期和短期养老服务床位数预测的需要，也提供了未来具有不确定性因素影响下的调整思路。为相关养老服务床位数的研究提供研究思路，为未来我国养老事业政策的制定和抉择提供理论依据。