应力比对不锈钢焊接接头疲劳寿命的影响研究

董鹏鹏 贺启林 王海洲 王儒文 杨 燕

（北京宇航系统工程研究所 深低温技术研究北京市重点实验室，北京 100076）

0 引言

0Cr18Ni9 不锈钢是一种高韧性奥氏体不锈钢，具有优良的力学性能、耐蚀性、耐热性等，广泛应用于运载火箭管路结构和飞机发动机管路结构部件中。在结构制造过程中，焊接是一种常用的连接方法，焊接接头的疲劳性能影响着结构的使用寿命［1-3］，研究0Cr18Ni9 不锈钢薄板焊接接头的疲劳性能具有重要的工程意义。

近年来，国内外对于焊接接头的高周疲劳（疲劳寿命N一般大于104次）寿命方面做了诸多的研究，张亚娟等［4］研究了不同厚度TA15钛合金电子束焊接接头的高周疲劳性能。雷星海等［5］利用SWT 疲劳损伤公式预测铝合金搅拌摩擦搭接焊接头疲劳寿命。何柏林等［6］研究了应力集中、晶粒细化、残余应力等因素对SMA490BW 钢对接接头高周疲劳性能的影响。张思倩等［7］研究了不同缺口半径和应力比对Ti-24Nb-4Zr-8Sn合金室温高周疲劳性能的影响。金雪等［8］针对0Cr18Ni9 及00Cr19Ni10 不锈钢焊接接头组织及其高周疲劳性能进行了研究。M. Sharifitabar等［9］研究了0Cr18Ni9 不锈钢的电阻对接焊以及焊接功率和对接压力对抗拉强度和疲劳寿命的影响。BAEK 等［10］研究了0Cr18Ni9 不锈钢管道母材及焊缝金属的断裂韧性和疲劳裂纹扩展性能。众多研究表明应力比对于疲劳强度和疲劳寿命有明显的影响［11-13］。米聪聪等［14］研究结果表明采用Walker 等效热点应力可以合理反映应力比对焊接接头高周疲劳寿命的影响。陈明等［15］结合Gerber、Goodman 以及Soderberg等3种应力修正方法，对Morrow-coffin 模型进行了修正。

本文通过设计疲劳试验，测试0Cr18Ni9 不锈钢薄板焊接接头疲劳极限和给定应力水平下疲劳寿命，确定其S-N曲线。基于试验结果，使用应力比的概念得到0Cr18Ni9 不锈钢薄板焊接接头Goodman 修正和Walker 修正的高周疲劳寿命预测模型，并将模型预测结果与试验中获得的疲劳寿命进行比较。

1 实验

1.1 单轴拉伸测试

选取厚度为2 mm 的0Cr18Ni9 不锈钢薄板，采用手工氩弧焊进行焊接，焊后维持焊缝余高和焊接形貌，并进行了X 光无损检测，焊接状态良好。3 件试样采用同批次原材料。

其母材化学成分和试样规格如表1 和图1 所示。常温力学性能测试按照GB/T 228.1—2010 进行测试，使用SANS CMT 5105 型电子万能试验机开展拉伸试验。试样平行段安装引伸计，采用恒位移速率控制，加载速率为2 mm/min。

表1 0Cr18Ni9不锈钢板化学成分Tab.1 The chemical composition of 0Cr18Ni9 stainless steel sheet%（w）

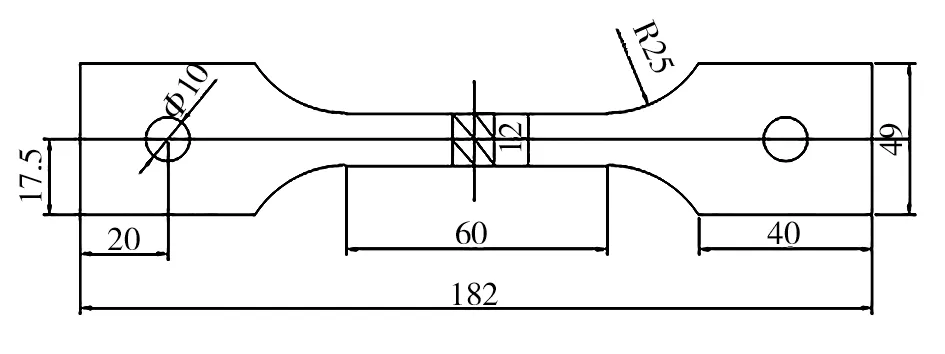
图1 0Cr18Ni9不锈钢薄板（2 mm）焊接接头拉伸试样Fig.1 0Cr18Ni9 stainless steel sheet（2 mm）welded joint tensile specimen

1.2 高周疲劳极限测试

试样选用0Cr18Ni9 不锈钢板材、厚度为2 mm 的手工氩弧焊接接头，按照GB/T 3075—2008［16］进行设计，试样轴线方向垂直焊缝，焊缝位于试样正中，试样及其尺寸如图2所示。疲劳试验在Zwick HFP5100高频疲劳试验机上进行，频率范围50～180 Hz，采用GB/T 24176—2009［17］中台阶法试验方案，给定一个最大应力水平（如400 MPa），设定疲劳寿命极限为107次，以一定的应力比开始试验。如试样循环107次未发生破坏（判定为未失效），则进行下一个试验时提高一定的应力水平，直至试样未循环至107次断裂（判定为失效）；以此应力水平为第一个试验，以该应力水平的5%或10%为应力台阶；第二个试样的应力水平为第一级应力水平减应力台阶，如试样在给定疲劳寿命内没有失效，则增加一个应力台阶，反之降低一个应力台阶。测试出至少15个参与计算的有效数据，根据试验结果计算疲劳极限平均值和标准差的统计值。试验测定了三个应力比下（R=0、0.2、0.5）0Cr18Ni9不锈钢薄板焊接接头的疲劳极限。

图2 0Cr18Ni9不锈钢薄板（2 mm）焊接接头试样Fig.2 0Cr18Ni9 stainless steel sheet（2 mm）weld joint specimen

1.3 高周疲劳寿命测试

与疲劳极限测试相同，材料的疲劳寿命试验在Zwick HFP5100高频疲劳试验机上进行，试样及其尺寸如图2所示。疲劳S-N曲线测试按照GB/T 3075—2008、GB/T 24176—2009进行，根据疲劳极限测试结果，选取5个等间距应力水平，以一定的应力比进行疲劳试验，记录试样失效时的疲劳寿命（循环周次）。每个应力水平的疲劳寿命应介于5 × 104～1 × 106。每个应力水平应至少测试6根试样。试验测定了三个应力比下（R=0、0.2、0.5）0Cr18Ni9不锈钢薄板焊接接头的S-N曲线。

2 结果与分析

2.1 单轴拉伸测试结果与分析

拉伸性能测试结果如表2所示，由测试结果计算得到名义应力-应变曲线，同时根据公式εtrue=In(1 +εnom)和σtrue=σnom(1 +εnom)将工程应力应变曲线转换为真实应力应变曲线，具体见图3。

从表2、图3 可见3 件同批次原材料焊接接头应力应变曲线的前半部分基本一致；强度和断裂位置存在一定差异。

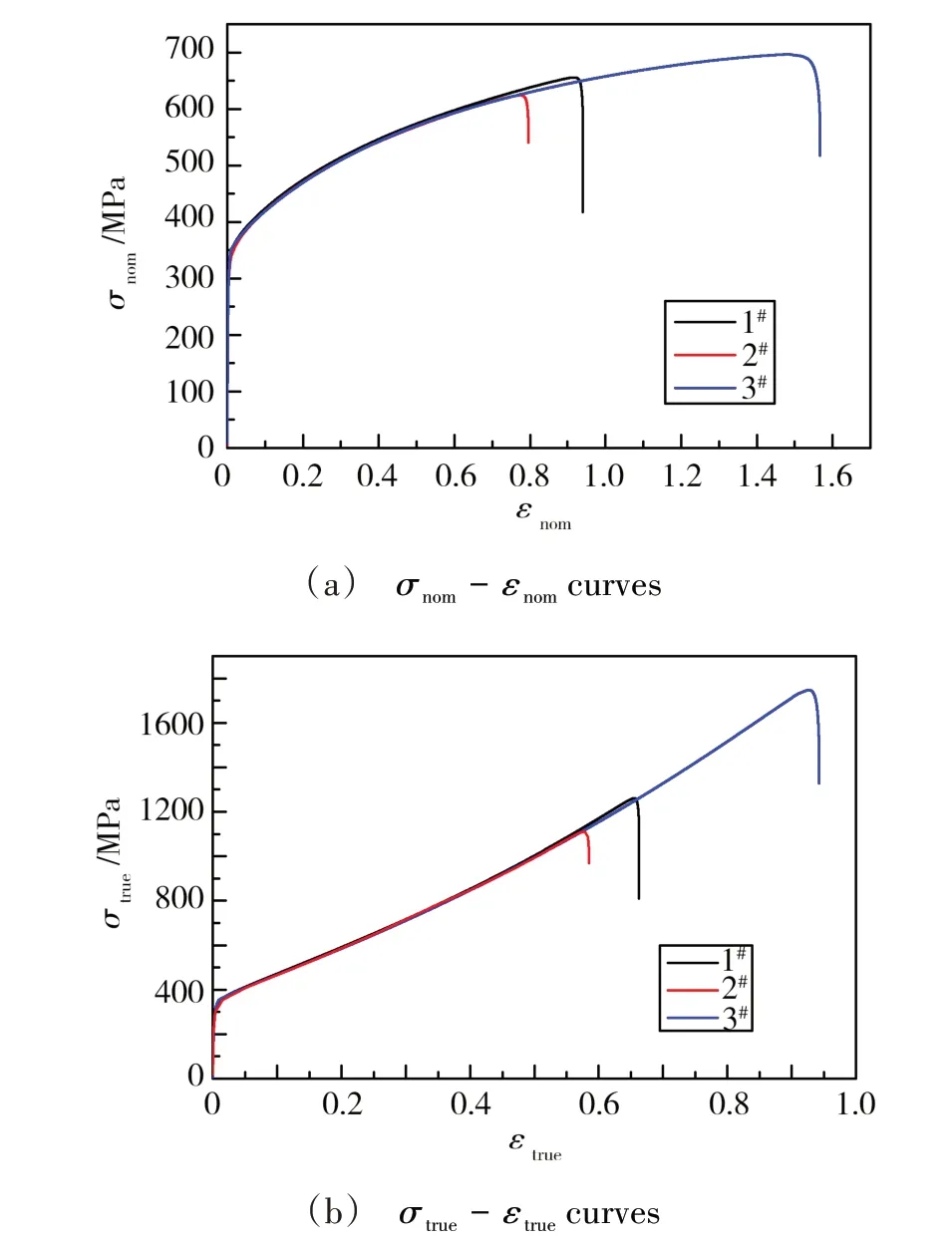
图3 0Cr18Ni9不锈钢薄板焊接接头单轴拉伸应力-应变关系Fig.3 Uniaxial tensile stress-strain relation of 0Cr18Ni9 stainless steel sheet welded joint

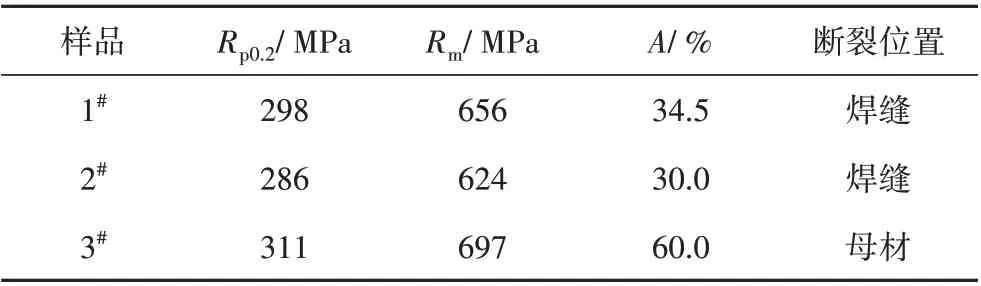
表2 0Cr18Ni9不锈钢薄板焊接接头力学性能Tab.2 Mechanical properties of 0Cr18Ni9 stainless steel sheet welded joints

焊接工艺过程的特性决定了焊缝余高的高度、形貌不可能完全一致，这就导致应力集中点位置、大小有差别，最大应力点/应变点位置不尽相同，因此会出现静强度断裂位置不同的现象。需要说明的是，尽管焊接接头的强度存在散差，但本试验的高周疲劳测试结果表明，所有的疲劳失效位置均在焊趾处。焊接接头强度散差对疲劳寿命的影响，最终反映在采用多个子样及其统计平均测试结果进行疲劳寿命曲线拟合上。

2.2 高周疲劳极限测试结果与分析

2.2.1R=0下测试结果与分析

应力比R=0 下共对15 个试样进行了试验，试样的最终断裂位置均在焊趾，如图4 所示，具体数据如表3 所示。表3 中疲劳寿命超过107次未发生断裂判定为未失效（N），反之判定为失效（Y）。

图4 焊接接头疲劳断口Fig.4 Fatigue fracture surface features of welded joint

根据GB/T 24176—2009 第7.2 节给出的计算方式，对表3 中试验数据进行统计分析如表4 所示。根据公式（1）、（2）计算平均疲劳极限估计值和标准差：

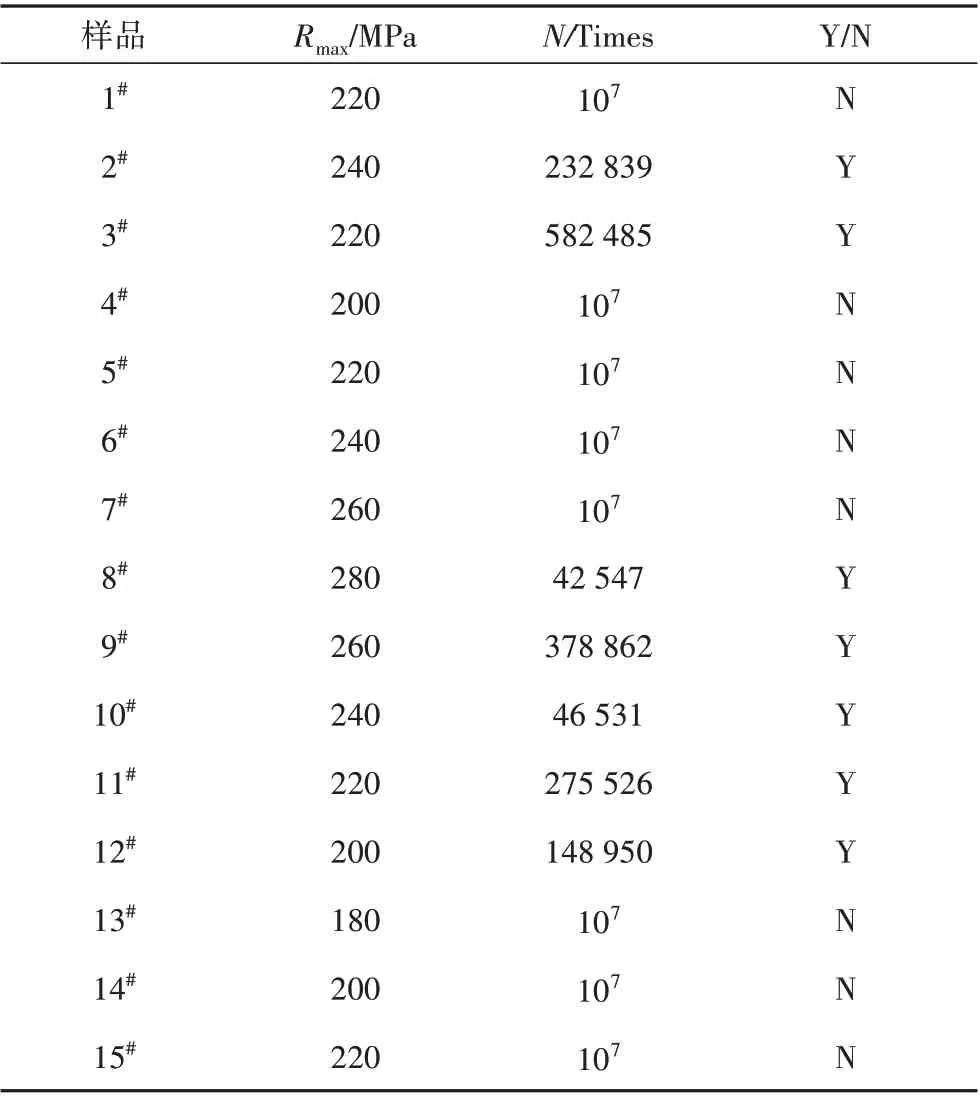
表3 疲劳极限测试数据汇总（R=0）Tab.3 Fatigue limit test data summary（R=0）

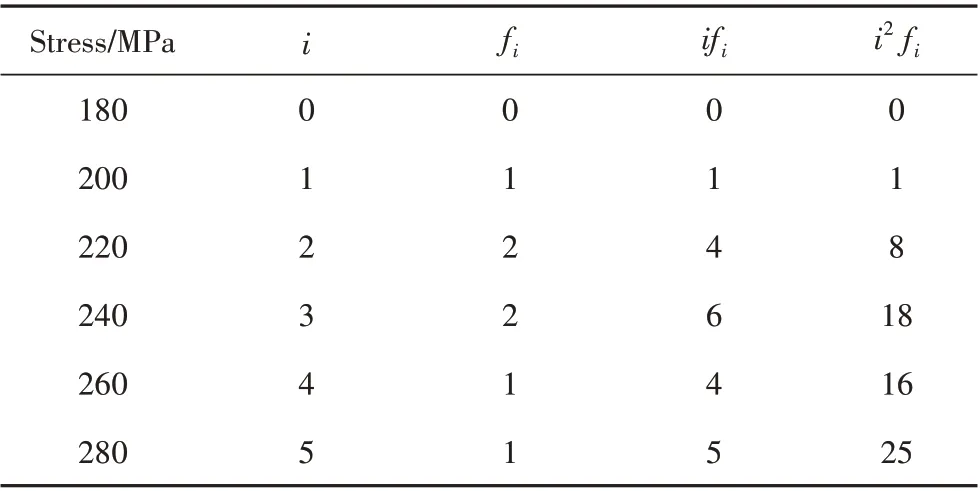
表4 疲劳极限测试数据分析（R=0）Tab.4 Fatigue limit testing data analysis（R=0）

2.2.2R=0.2下测试结果与分析

在R=0.2下，采用和R=0相同的方法开展了疲劳极限测试。共对15 个试样进行了试验，断裂位置均在焊趾，统计数据如表5所示。

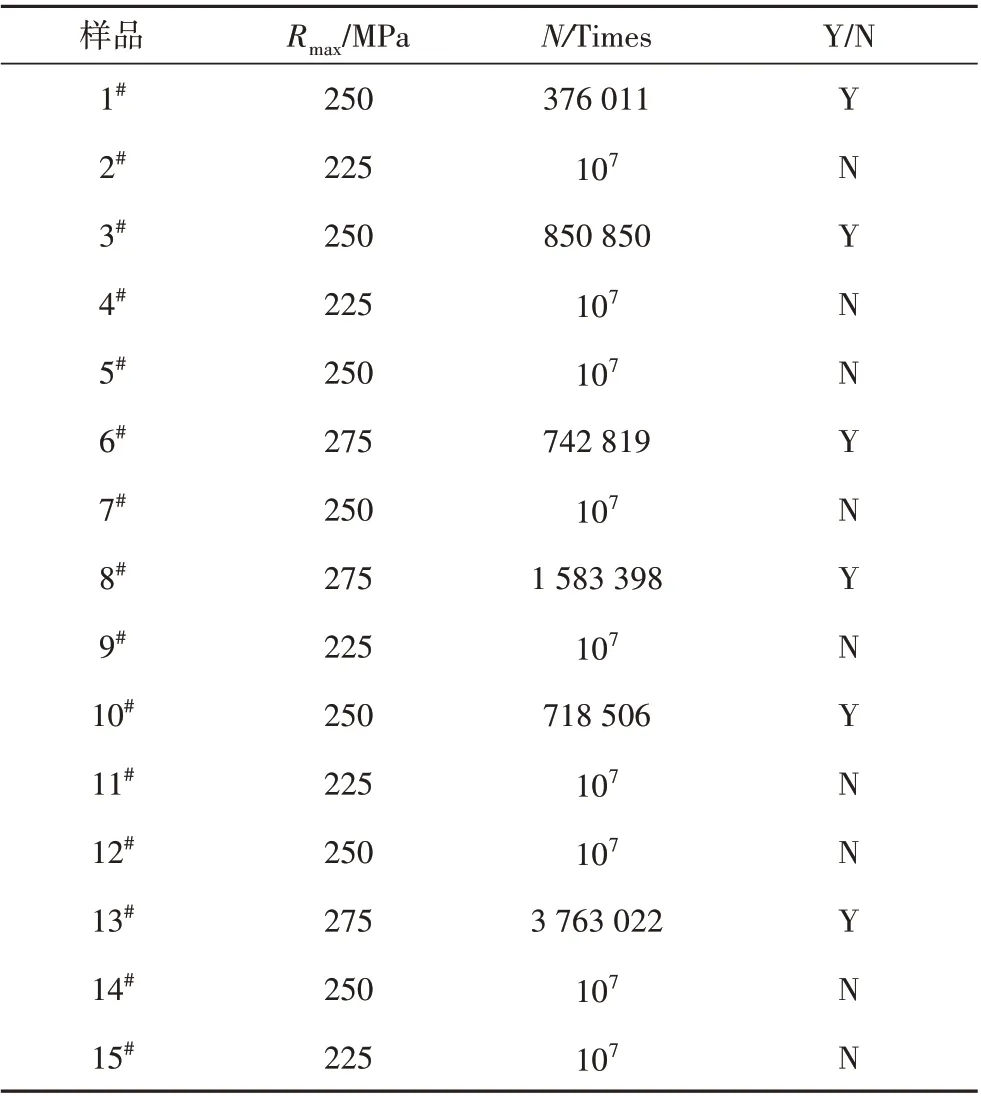
表5 疲劳极限测试数据汇总（R=0.2）Tab.5 Fatigue limit test data summary（R=0.2）

同样对以上试验数据进行统计分析如表6所示。与2.2.1 相同，计算平均疲劳极限估计值和标准差如下：

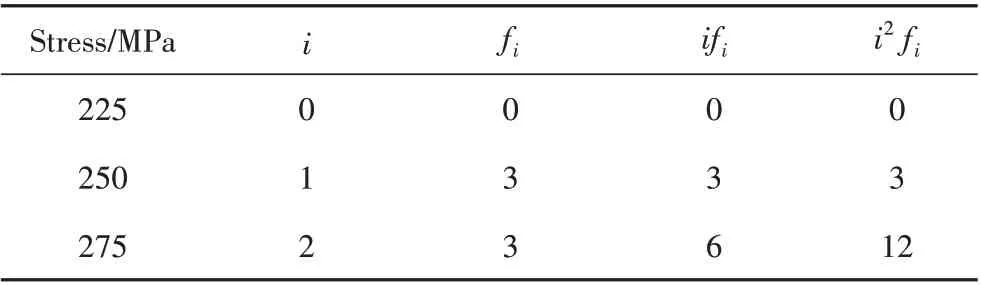
表6 疲劳极限测试数据分析（R=0.2）Tab.6 Fatigue limit testing data analysis（R=0.2）

2.2.3R=0.5下测试结果与分析

试验前计划测试15个参与疲劳极限计算的有效数据，实际中发现，焊接接头在360 MPa 应力水平下不发生断裂，而在390 MPa 下均发生断裂，且循环周次较为接近，因此将实际试验数据量减少为8 个，参与计算的试样数量为7个，具体数据如表7所示。

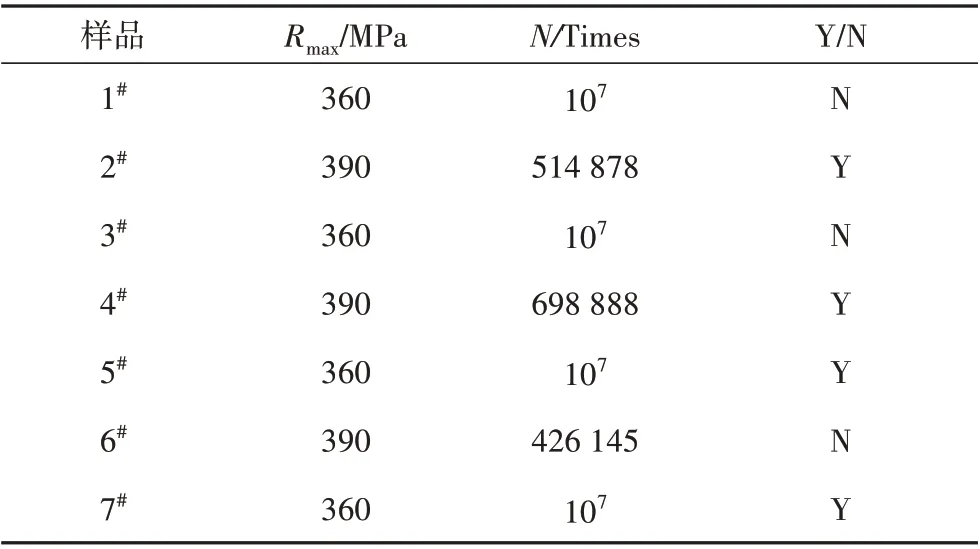
表7 疲劳极限测试数据汇总（R=0.5）Tab.7 Fatigue limit test data summary（R=0.5）

对以上试验数据进行统计分析如表8所示，计算平均疲劳极限估计值如下：

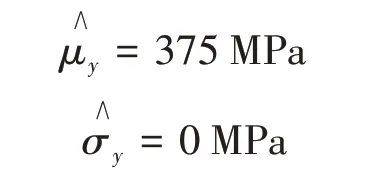
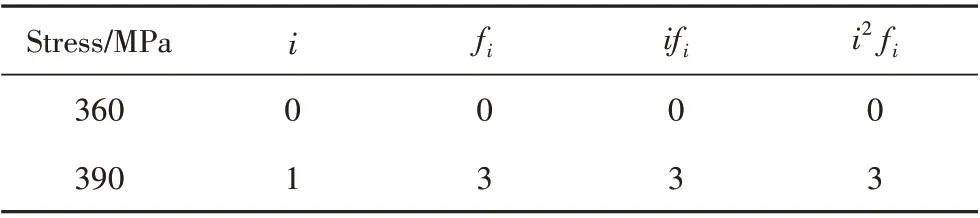
表8 疲劳极限测试数据分析（R=0.5）Tab.8 Fatigue limit testing data analysis（R=0.5）

2.3 高周疲劳寿命测试结果与分析2.3.1 R=0下测试结果与分析

在应力比R=0下，共进行了5个应力水平下的疲劳寿命测试，结果见表9。绘制的疲劳S-N曲线如图5 所示，其中S为最大应力，下同。可得到如（3）、（4）式两种线性拟合结果。

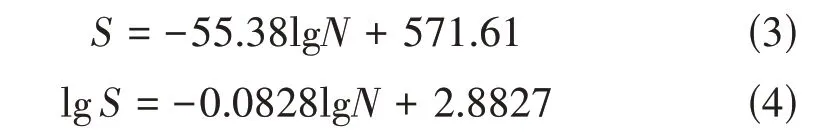
表9 给定应力水平下疲劳寿命测试数据Tab.9 Fatigue life test data at a given stress level

两种方式线性拟合程度接近，均可作为270～310 MPa 应力水平范围内S-N的线性关系。因此在应力比R=0 时，高周范围内（5 × 104≤N≤1 × 106）S-N线性关系可用公式（3）、（4）表示。

2.3.2R=0.2下测试结果与分析

在应力比R=0.2 条件下，疲劳寿命测试结果如表10 所示。绘制焊接接头的疲劳S-N曲线如图5 所示，其线性拟合结果见式（5）、（6）。

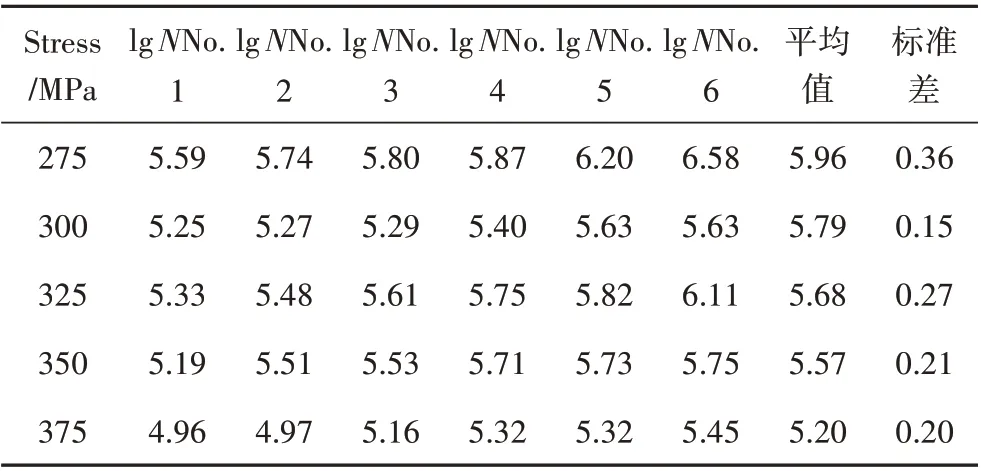
表10 给定应力水平下疲劳寿命测试数据Tab.10 Fatigue life test data at a given stress level

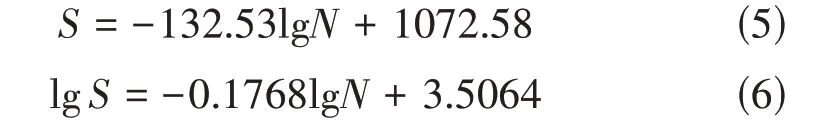
式（5）、式（6）均可作为275～375 MPa应力水平范围内S-N的线性关系。

2.3.3R=0.5下测试结果与分析

在应力比R=0.5 下，疲劳寿命测试结果如表11所示，其疲劳S-N曲线如图5所示，并得到如下关系：

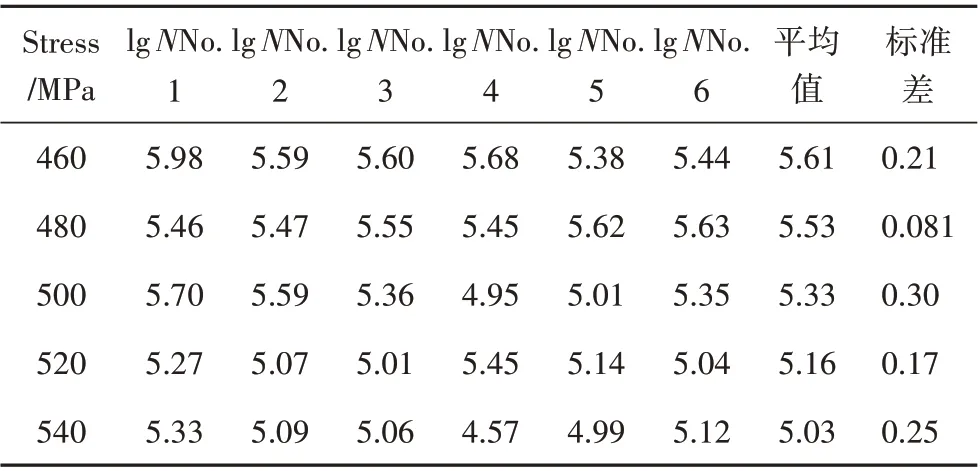
表11 给定应力水平下疲劳寿命测试数据Tab.11 Fatigue life test data at a given stress level

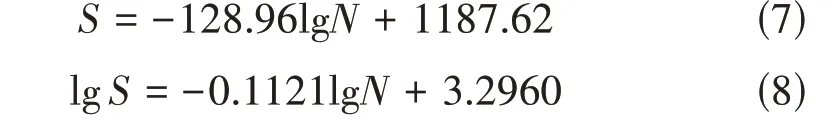
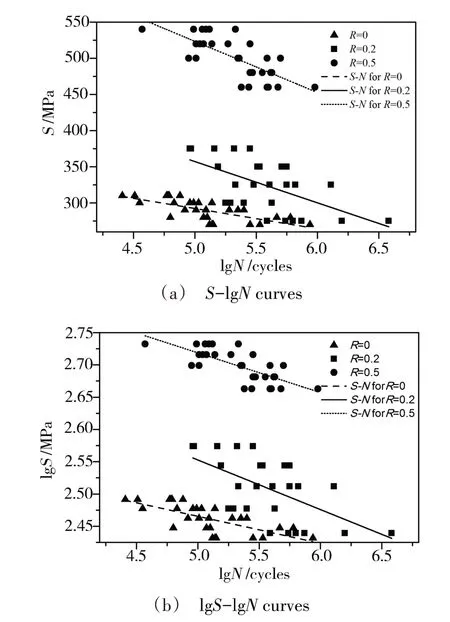
图5 0Cr18Ni9不锈钢薄板焊接接头疲劳S-N曲线Fig.5 0Cr18Ni9 stainless steel sheet welded joint fatigue S-N curves

式（7）、式（8）均可作为460～540 MPa应力水平范围内S-N的线性关系。

由图5 可见，应力比（R=0、0.2、0.5）对0Cr18Ni9不锈钢薄板焊接接头的疲劳S-N曲线有较大的影响，对于不同的应力比，试验结果的散点图分散带不同。另外，在同一应力水平状态下，应力比越大其循环周次N越大。在应力比R=0条件下，试样受力状态最为严酷，其疲劳极限最低。

3 考虑应力比影响的高周疲劳寿命预测

3.1 预测模型

试验结果表明应力比对疲劳寿命有较大的影响，应力比对疲劳强度的影响可归因于平均应力对疲劳强度的影响［18］，目前有多种平均应力修正的预测疲劳寿命模型，本文采用Goodman和Walker［19-20］修正的连续损伤力学模型对0Cr18Ni9不锈钢薄板焊接接头疲劳寿命进行比较分析。一般用来描述循环载荷的公式如下：

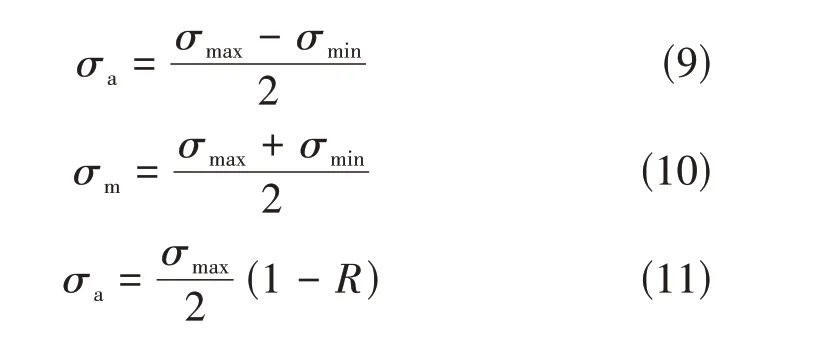
式中，σa为应力幅，σm为平均应力，R为应力比，而描述平均应力效应的Goodman和Walker方程如下。

Goodman［21］方程：

式中，σu为拉伸极限强度。

Walker［21］方程：

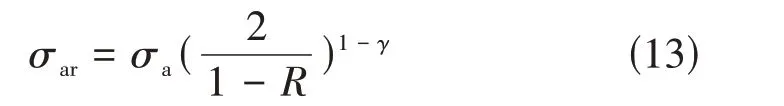
式中，σar为等效应力幅，γ为材料的独立参数。

对于高周疲劳来说，一般将考虑平均应力影响的损伤演化方程描述如下［20］：

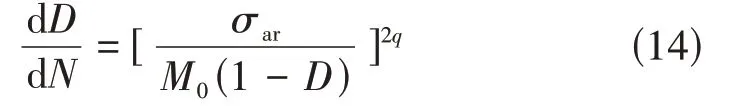
式中，D为损伤度，取材料初始（N=0）损伤D=0，当破坏发生时损伤累积至1，即D=1。

将式（12）、式（13）分别代入式（14），经过推导即可以得出分别采用Goodman 修正和Walker 修正的连续损伤力学模型下应力与寿命关系［20］。

采用Goodman修正的高周疲劳寿命预测模型：

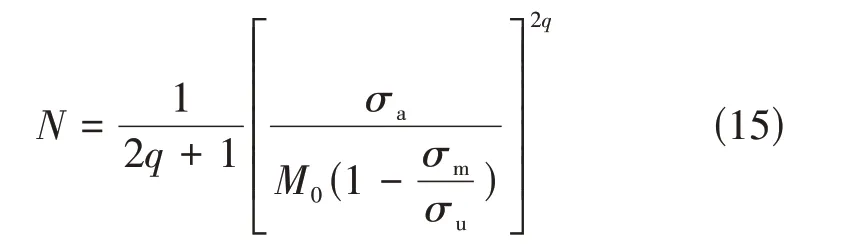
式中，M0、q为待定系数。

采用Walker修正的高周疲劳寿命预测模型：

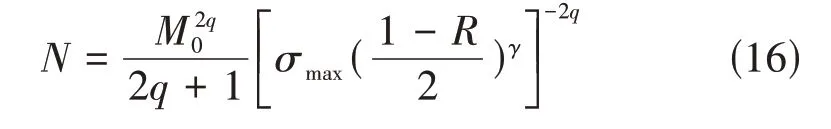
式中，M0、q、γ为待定系数，式（15）、式（16）中待定系数可以对试验的S-N数据进行多元回归分析得到，再反代回方程，即可对高周疲劳的寿命进行估计。

将式（15）两边取对数，即可得到如下方程：

利用试验数据进行多元函数线性拟合，即可得到相应模型参数，拟合结果如下。

采用Goodman修正的高周疲劳寿命预测模型：

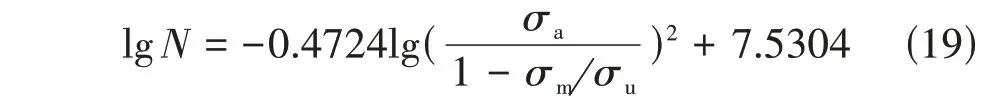
采用Walker修正的高周疲劳寿命预测模型：

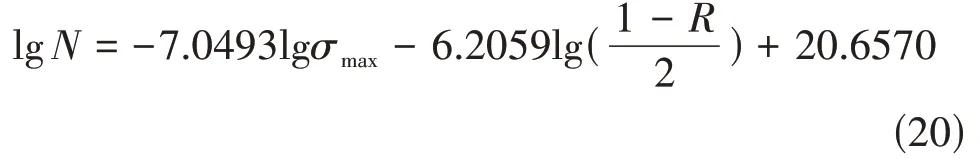
3.2 试验验证

将两种模型预测效果与试验数据对比，如图6所示分别为在不同的应力比下，Goodman 修正模型、Walker修正模型与试验结果的对比。

由图6 可见，在不同应力比（R=0、0.2、0.5）下，采用Walker 修正的高周疲劳寿命预测模型能较好地描述试验数据的变化趋势，偏差较小。采用Goodman修正的预测模型与试验数据的偏差较大，Walker 修正的预测疲劳寿命模型更能反映应力比的影响。

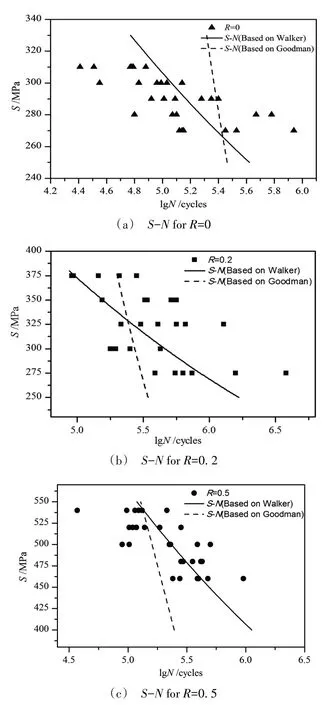
图6 Walker模型、Goodman模型与试验数据对比Fig.6 Comparison of Walker model，Goodman model and experimental data

在不同应力比（R=0、0.2、0.5）和不同的应力水平下，将试验测得S-N曲线与基于Walker和Goodman修正的疲劳寿命预测模型相比如图7所示。图中的数据点分别为试验S-N曲线与修正模型预测的疲劳寿命。不同应力比下的应力水平按表9～表11选取。

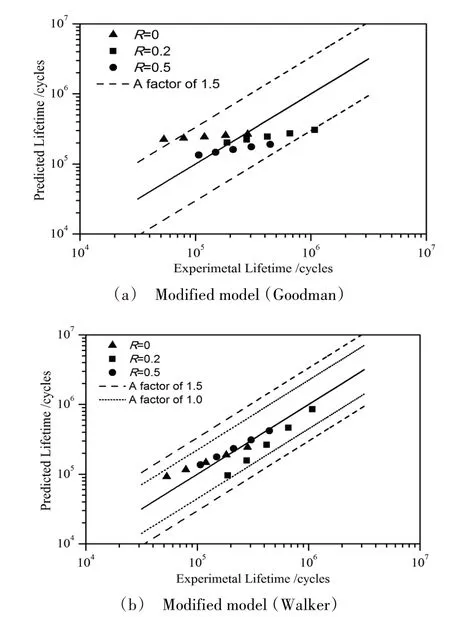
图7 寿命估算结果与试验结果对比Fig.7 Comparison of life estimation results with experimental results

从图中可以看出，对于0Cr18Ni9 不锈钢薄板焊接接头，Walker 修正模型对该材料的疲劳寿命预测结果全部处于1.0倍试验结果的标准差分散带以内，而基于Goodman 修正模型的寿命预估结果大部分处于1.5倍试验结果的标准差分散带内，但不同应力比下，Walker 修正模型与试验数据拟合得更好，这说明采用Goodman 平均应力修正的连续损伤力学模型有所不足。采用Walker 修正的高周疲劳损伤模型预测结果更为准确。

3.3 模型对比分析

由3.1可以看出，Goodman修正和Walker修正的连续损伤力学模型的不同在于等效应力幅σar不同，将其作对比可得到如下表达式：

明显当Y=1时，Goodman修正和Walker修正的等效应力幅相同，因此两种模型预测结果应该相同。Y随R、σmax的变化曲线如图8 所示，取应力比的范围为-1～1。

图8 等效应力幅之比与应力比的关系Fig.8 Relationship between equivalent stress amplitude ratio and stress ratio

从图8 可以看出，在应力比R= -1 时，Y=1，此时两种修正模型预测效果相同。当循环载荷最大值一定时，其循环载荷应力比越大，两种修正模型的预测效果相差越大。同一应力比下，循环载荷最大值越大，两种模型的预测效果相差越大。在应力比接近于1 时，由于其等效应力幅接近于0，因此曲线会趋于无限大。

4 结论

（1）研究了0Cr18Ni9 不锈钢薄板焊接接头的高周疲劳性能，通过试验测得其不同应力比下（R=0、0.2、0.5）焊接接头的疲劳极限和给定应力水平下的疲劳寿命，得到了其S-N曲线。

（2）试验结果表明不同的应力比，散点图分散带不同，说明应力比对0Cr18Ni9 不锈钢薄板焊接接头的疲劳S-N曲线有较大的影响。同一应力水平状态下，应力比越大其循环周次N越大。在应力比R=0下，试样受力状态最为严格，其疲劳极限强度最低。

（3）基于试验结果，使用应力比的概念得到了0Cr18Ni9 不锈钢薄板焊接接头Goodman 修正和Walker 修正的高周疲劳寿命预测模型，并与试验数据进行了对比。结果表明两者均能体现应力比对疲劳寿命的影响，但Walker修正的模型误差更小，采用Walker 修正的高周疲劳寿命模型预测结果处于1.0倍分散带以内，效果更好。