基于NARX神经网络辅助组合导航方法研究

张 帅， 郑龙江， 侯培国

(燕山大学 电气工程学院，河北 秦皇岛 066004)

捷联惯性导航系统(Strap-down Inertial Navigation System,SINS)和全球导航卫星系统(Global Navigation Satellite System,GNSS)相组合是广泛应用的一种车载组合导航形式，这是由SINS、GNSS的互补特性所决定的。对于工作在城市环境中的乘用车辆来说有两个特点，第一个特点是车辆工作环境中存在高楼、树木、立交桥和隧道等，卫星信号易受到干扰或遮挡进而导致短时GNSS失效，组合导航滤波器因缺少量测量而无法进行量测更新，使得组合导航系统等同于工作在纯惯性导航状态；第二个特点是乘用车辆一般装配由微机电系统(Micro Electro Mechanical System，MEMS)工艺制造的捷联惯性导航系统，一旦GNSS系统失效，惯性导航误差会在短时间内累积到不可接受的程度。为解决短时GNSS失效的情况下，组合导航精度急剧下降的问题，国内外学者进行了研究并提出了不同的解决思路。一种思路是对GNSS系统进行强化[1]或对组合导航滤波算法进行改进[2]。另一种思路是向组合导航系统中添加一种或多种辅助传感器，如里程计[3]与视觉里程计[4]等，或者向组合导航系统中引入一种辅助定位技术，如超宽带定位技术[5]、基于车联网的协同定位技术[6]等。除上述两种思路外，还可以通过分析车辆运动特性和导航误差特性、以及运动状态与导航误差间的关系，得到虚拟量测量或导航误差预测值，进而对导航误差进行补偿。如非完整约束[7]和零速更新技术[8]依据运载体运动特性得到虚拟量测量，保障组合导航滤波器的正常工作。支持向量机[9]、极限学习机[10]、自适应神经模糊推理系统[11]等辅助方法的研究重点是载体运动状态、惯性传感器输出以及导航误差间的关系。

人工神经网络具有良好的自学习和拟合能力，可以使用神经网络对惯性导航输出与导航误差或卫星导航输出之间的关系进行学习训练。当GNSS系统失效时，由神经网络辅助惯性导航系统工作，维持导航精度。可用于辅助组合导航系统工作的人工神经网络种类有很多，如采用径向基函数为隐藏层神经元传输函数的径向基神经网络[12]、通过增加隐藏层数量提高网络非线性拟合能力的多层感知器神经网络[13]、具有局部回归结构和记忆能力的Elman神经网络[14]和NARX(全称Nonlinear Autoregressive with External Input)神经网络[15]、具有记忆单元和门控单元结构的长短期记忆神经网络[16]和GRU(Gated Recurrent Unit)循环神经网络[17]等。

提出一种基于NARX神经网络辅助的组合导航方法，利用NARX神经网络的记忆能力和拟合能力，构建起惯性测量单元(Inertial Measurement Unit，IMU)输出信息、SINS解算信息与GNSS输出信息间的非线性关系。通过实验证明，短时GNSS失效的情况下，所提出的组合导航方法能够消减GNSS失效对组合导航系统造成的影响，使导航误差维持在可接受范围内。

1 SINS/GNSS组合导航

SINS短时精度高、导航参数完整，但导航误差会随时间累积。GNSS导航误差的主要来源是导航信号经大气层传输产生的延迟误差和多路径效应误差、导航卫星端的星钟和星历误差、导航接收端的钟差和天线造成的误差等，GNSS导航误差与系统工作时长无关，导航误差不会随时间累积，但GNSS易受环境干扰造成导航信号中断。SINS/GNSS组合导航系统以SINS为主系统，在GNSS可用时对SINS误差进行校正，解决SINS误差随系统工作时长增加而不断累计的问题。在组合导航中，SINS所提供的导航信息来自于惯性传感器陀螺仪和加速度计。陀螺仪用于测量角运动信息，一般输出为角度增量。加速度计用于测量线运动信息，一般输出为速度增量。

SINS/GNSS组合导航按组合紧密程度可划分为松组合、紧组合以及超紧组合，本文采用松组合形式对SINS和GNSS信息进行融合。在松组合形式中，将GNSS提供的位置速度信息与SINS解算得到的位置速度信息做差作为滤波器量测量，通过量测更新对SINS导航误差进行修正，维持较高的导航精度。

采用卡尔曼滤波方法对来自GNSS和SINS的信息进行融合，导航坐标系选择东北天坐标系。卡尔曼滤波状态量包括3轴失准角、3维速度误差、3维位置误差、3轴陀螺仪零偏、3轴加速度计零偏，量测量包括3维位置和速度误差。式(1)和式(2)分别为状态方程和量测方程。

Xk=Φk,k-1Xk-1+Γk-1Wk-1

(1)

Zk=HkXk+Vk

(2)

式中:X为状态量矩阵；Z为量测量矩阵；Φ为状态转移矩阵；Γ为系统噪声驱动阵；W为系统噪声矩阵；H为量测矩阵；V为量测噪声矩阵[18]。

状态转移矩阵、噪声驱动阵以及系统噪声矩阵中包含着系统动态特性的相关信息，可用于评价系统状态估计预测值的质量。量测矩阵表示量测信息与各状态量间的关系，量测噪声矩阵包含量测噪声特性，可用于评价量测信息的质量。综合系统状态估计预测值和量测信息的质量评价，最终决定量测值和状态估计预测值的利用比例。

2 NARX神经网络

2.1 NARX神经网络介绍

NARX神经网络是一种递归动态神经网络，具有短期记忆能力，与静态神经网络相比，NARX神经网络能够更好地学习复杂动态系统输入与输出间的关系。应用在组合导航系统当中，能够更好地根据IMU输出信息和惯性导航解算信息给出GNSS位置速度信息的预测值。NARX神经网络当前时刻的输出取决于当前时刻网络输入、若干以前时刻的输入以及若干以前时刻的输出。神经网络输入输出关系如式(3)所示。

yt=f(xt,xt-1,…,xt-nx,yt-1,…,yt-ny)

(3)

式中:yt为神经网络输出；f(·)为非线性函数；xt为神经网络输入；nx,ny分别为输入延迟数和输出反馈延迟数。

2.2 神经网络结构和训练方法

只要有足够的隐藏层神经元，一个隐藏层采用S型传输函数、输出层采用线性传输函数的两层网络几乎能以任意精度逼近任意函数[19]，所以本文使用的NARX神经网络只包含1个隐藏层，隐藏层神经元采用tansig传输函数，输出层采用线性传输函数。tansig函数在数学上是连续可微的、严格递增函数，便于使用计算机对神经元进行训练。依据神经网络训练经验，将当前时刻和上一时刻的惯性导航信息作为神经网络输入，可以达到较好的组合导航效果，所以本文创建的NARX神经网络输入输出延迟数均设置为1。隐藏层神经元数目对组合导航的效果有较大的影响，神经元数目过少则神经网络无法对输入输出关系进行良好的拟合，神经元数目过多会造成神经网络训练参数过多、训练时长增加，而且当神经元数量过多时，在训练数据上，神经网络将会出现过拟合，尽管在训练数据上的训练误差很小，但神经网络不能很好地辅助导航，所以依据神经网络训练经验将隐藏层神经元数目设置为10个。

网络训练方法采用LM(Levenberg-Marquardt)算法，LM算法是牛顿法的一个改进，用于最小化非线性函数平方和，非常适用于对采用均方误差为性能指标的神经网络进行训练。在网络参数个数适中的情况下，LM算法有较快的训练速度。

3 神经网络辅助原理

3.1 神经网络辅助原理分类

神经网络辅助组合导航系统的总体思路都是在GNSS状态良好时对神经网络进行训练，当GNSS失效时神经网络由训练模式切换到预测模式，根据IMU和惯性导航解算信息给出系统所需的辅助导航信息，维持组合导航精度。

根据神经网络与组合导航滤波器的关系，可以将神经网络辅助导航系统分为两类。一类是GNSS系统失效时，神经网络直接取代组合导航滤波器，由神经网络依据IMU和惯性导航解算信息给出惯性导航误差，对惯性导航进行修正，达到维持导航精度的目标。另一类方法中神经网络并不提供惯性导航误差的预测值，而是给出GNSS失效期间组合导航滤波器所需量测量的预测值，进而保障组合导航滤波器量测更新的正常进行，最终达到维持导航精度的目标。根据神经网络给出组合导航滤波器所需量测量预测值的方式，可分为直接给出和间接给出两种。直接给出的方式是由神经网络直接根据IMU和惯性导航解算信息给出组合导航滤波器所需量测量的预测值，在SINS/GNSS松组合导航中滤波器所需量测量为GNSS输出和惯性导航解算位置、速度的差值。间接给出的方式是由神经网络给出GNSS位置、速度信息的预测值，之后将此预测值与惯性导航解算的位置、速度信息做差后得到组合导航滤波器所需的量测量。

GNSS失效造成的直接结果就是GNSS位置速度信息的缺失，用神经网络对GNSS位置速度进行预测能够减少中间环节，简化网络输入输出关系，降低网络学习负担，加快网络学习速度。所以本文提出的NARX神经网络辅助导航方法中，神经网络用于给出GNSS位置速度增量的预测值，将预测值与惯性导航解算信息做差后得到组合导航滤波器所需量测量，保证卡尔曼滤波量测更新的正常进行。

3.2 神经网络输入输出信息选择

神经网络的输入输出信息选择方面，可供选择的输入信息有IMU提供的角速度ω和比力f，惯性导航解算输出的姿态角aSINS、速度VSINS、位置PSINS，GNSS输出的速度VGNSS、位置PGNSS，以及时间信息t。最终目标信息为SINS和GNSS位置速度差值δP、δV。GNSS失效期间，t时刻SINS和GNSS位置速度差值δPt、δVt可由式(4)表示。

(4)

式中：δPt、δVt分别为t时刻SINS与GNSS位置、速度差值；ΔPSINS(t)、ΔPGNSS(t)分别为t时刻SINS位置增量、GNSS位置增量；ΔVSINS(t)、ΔVGNSS(t)分别为t时刻SINS速度增量、GNSS速度增量；Pt-1、Vt-1分别为t-1时刻组合导航的位置、速度信息。

选用增量信息而不是位置速度的绝对值有利于神经网络的训练，故本文选择GNSS位置速度增量信息作为神经网络目标输出。

式(5)、式(6)为惯性导航速度方程[20]。

(5)

(6)

由式(5)和式(6)可知，速度与姿态角、比力和位置间有复杂的非线性关系，如式(7)所示。

(7)

式中:ΔPn为导航坐标系下三维位置增量；Vn为导航坐标系下三维速度。

由式(7)位置增量可以表示为加速度的二重积分。因而SINS位置和速度增量与IMU输出间存在非线性关系。GNSS和SINS固连在运动载体上，理想情况下GNSS和SINS的速度和位置增量应一致，但由于各种传感器自身误差和外界干扰的存在，GNSS和SINS的速度和位置增量间也存在较为复杂的非线性关系。所以选择IMU输出信息以及惯性导航解算输出的位置和速度增量作为神经网络输入信息。由于使用的神经网络为NARX神经网络，其自身具有时间延迟和记忆功能，不考虑时间信息作为神经网络输入。最终选择IMU输出的3轴角速度、3轴加速度，惯性导航解算得到的东向位置和速度增量、北向位置和速度增量，共计10维信息作为神经网络输入。选择GNSS东向位置和速度增量、北向位置和速度增量作为神经网络目标输出。

3.3 组合导航系统的两种工作状态

经过上述分析，确定了神经网络与组合导航滤波器关系和神经网络输入输出信息。接下来详细描述提出的NARX神经网络辅助组合导航方法中组合导航系统的两种工作状态。在图1所示的训练模式下，IMU输出角速度ω和比力f到惯性导航解算单元解算得到SINS输出的位置增量ΔPSINS和速度增量ΔVSINS，将ΔPSINS和ΔVSINS与GNSS输出的位置增量ΔPGNSS、速度增量ΔVGNSS送入组合导航滤波器作差后得到位置、速度差值δP和δV，将其作为卡尔曼滤波量测信息进行量测更新，卡尔曼滤波输出位置、速度误差对SINS进行修正后得到组合导航输出的位置P、速度V。NARX神经网络接收IMU测量信息ω、f和SINS位置速度增量ΔPSINS、ΔVSINS作为网络输入，GNSS位置速度增量ΔPGNSS、ΔVGNSS作为网络目标输出进行神经网络训练。

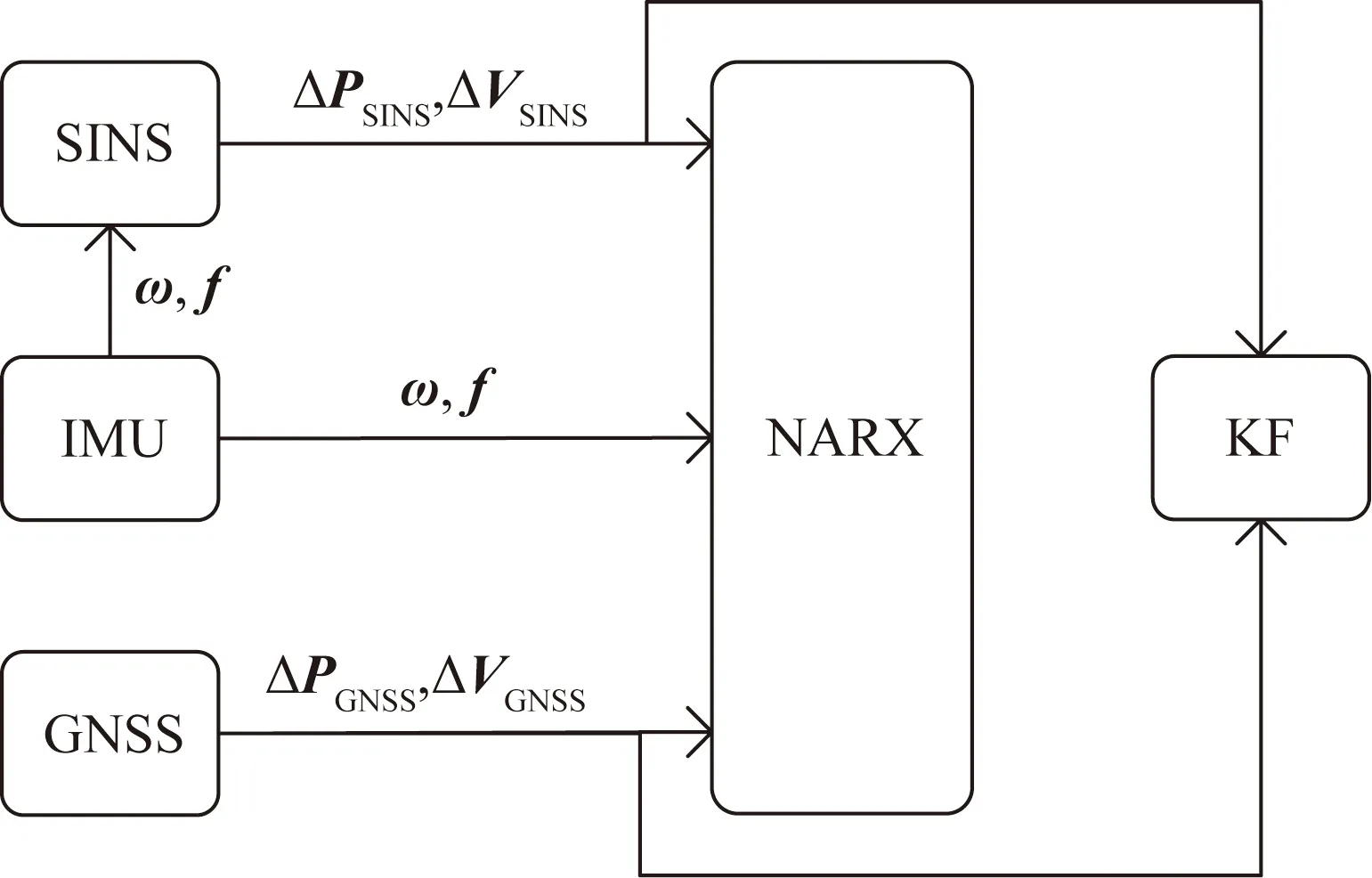
图1 训练模式

预测模式如图2所示，GNSS失效期间，组合导航系统切换到预测模式，神经网络根据输入的角速度ω、比力f以及SINS位置速度增量ΔPSINS、ΔVSINS，给出GNSS位置速度增量ΔPGNSS、ΔVGNSS的预测值。将该预测值与SINS位置速度增量送入组合导航滤波器作差后得到卡尔曼滤波所需的量测量δP和δV，保证滤波器量测更新的顺利进行，进而对惯性导航误差进行修正，维持组合导航精度。

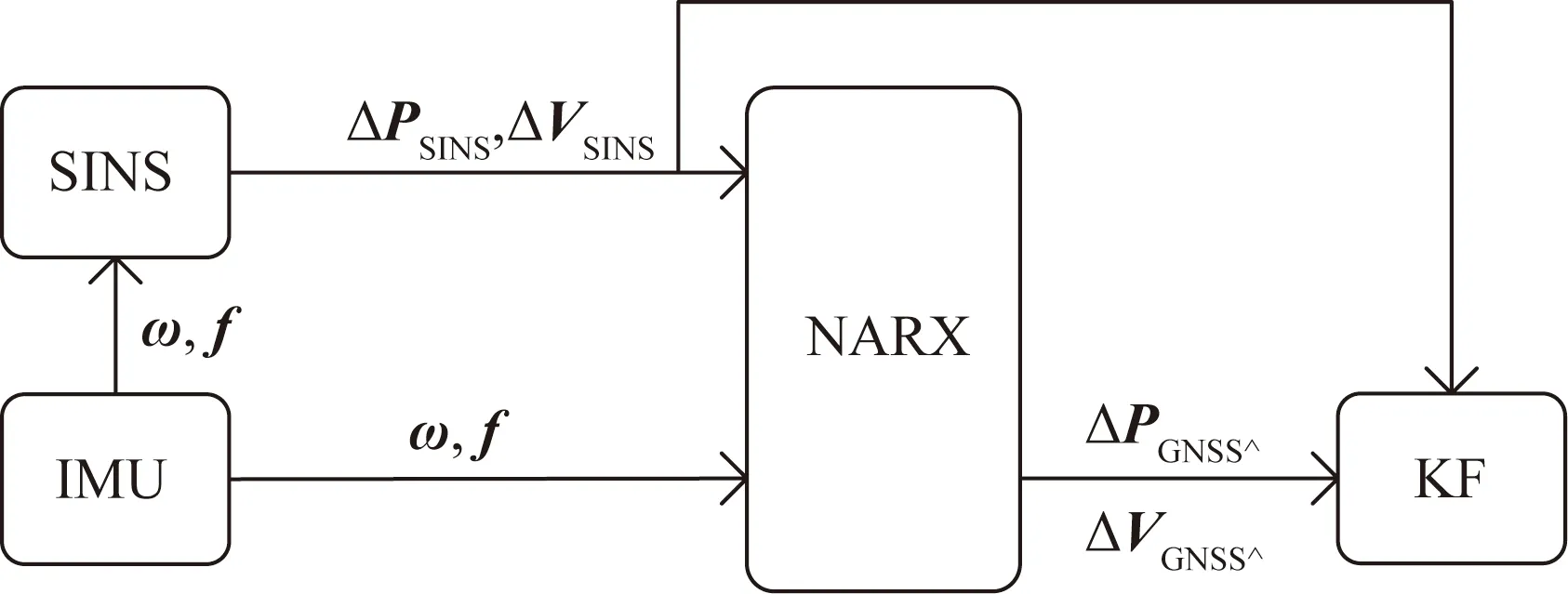
图2 预测模式

4 实验和结果分析

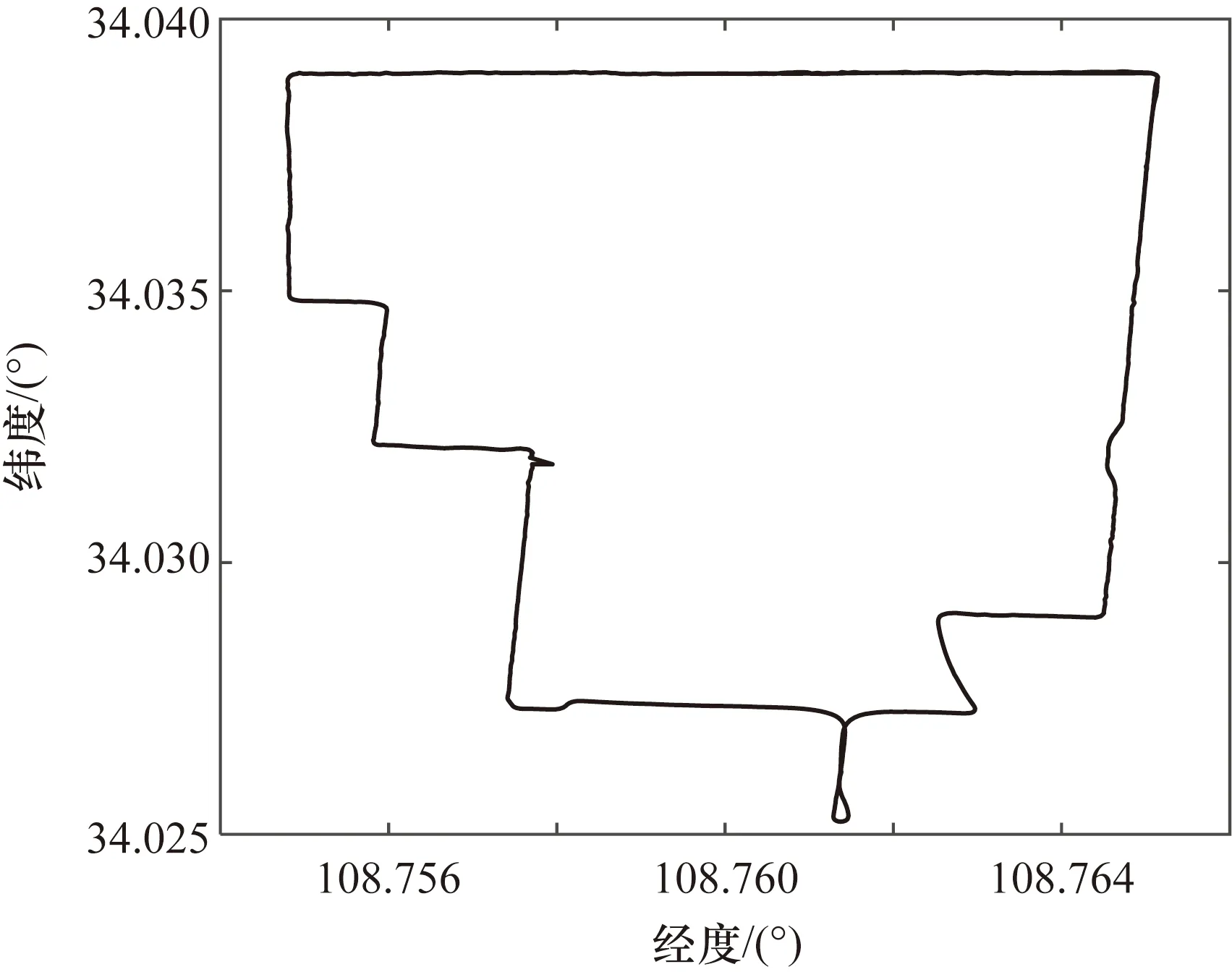
图3 卫星输出轨迹

为了验证提出方法的有效性、NARX神经网络的优越性，以及相较于现有方法，所提出方法的优势，设置3个对照方法实验。对照方法一：GNSS失效期间不进行任何辅助措施，使组合导航工作于纯惯性导航状态；对照方法二：GNSS失效期间，由BP神经网络对组合导航进行辅助，所创建的BP神经网络包含1个隐藏层，隐藏层中包含10个神经元，传输函数为tansig，网络输入、目标输出以及训练算法与前述NARX网络保持一致；对照方法三：GNSS失效期间由NARX神经网络对组合导航进行辅助，所创建的NARX神经网络包含一个隐藏层，隐藏层中包含20个神经元，传输函数为tansig，网络输入为速度、航向角、俯仰角和横滚角，目标输出为经纬度增量，输入延迟数为1，输出反馈延迟数为2。

另外为方便图例表示，将提出的NARX神经网络辅助方法列为方法四，所创建的NARX神经网络包含一个隐藏层，隐藏层中包含10个神经元，传输函数为tansig，网络输入为IMU测量信息、惯性导航解算得到的东向位置和速度增量、北向位置和速度增量信息，目标输出为GNSS东向位置和速度增量、北向位置和速度增量，输入延迟数和输出反馈延迟数均为1。

以组合导航系统正常工作解算出的位置和速度为导航信息真值；GNSS失效的情况下，以不同方法给出的位置和速度为导航信息实验值。将真值与实验值作差，可以得到不同方法的导航误差，根据该误差可以判断不同组合导航方法的效果。导航误差越小、误差曲线越平稳，证明该方法减少GNSS失效对组合导航影响的能力越强。由于滤波初期输出的位置信息波动较大，不利于运动轨迹的清晰显示，并且为了突出GNSS失效时段内不同方法输出轨迹的区别，仅给出了1200～1500 s的导航轨迹。不同方法辅助导航的运动轨迹如图4所示。

图4 组合导航轨迹

图4中，黑色虚线为GNSS正常工作情况下由卡尔曼滤波对GNSS信息和SINS信息融合后输出的轨迹，作为理想运动轨迹。有红色叉号标记的区间为模拟GNSS失效区间，时长60 s。1240 s以前，GNSS正常工作，组合导航系统不受任何干扰，不同方法输出的运动轨迹基本重叠。1240～1300 s为GNSS失效区间，不同方法输出的运动轨迹出现较大差别。蓝色虚线(方法一)为纯惯性导航推算模式下输出的运动轨迹，与理想运动轨迹有明显偏差，理想轨迹近似一个去掉底边的矩形，方法一的输出轨迹自GNSS失效起就有一个较大的航向角偏差，到转角处航向角偏差进一步增大，轨迹偏差在1300 s左右达到最大(见图5)。红色实线(方法二)和红色虚线(方法三)分别代表BP神经网络和现有的一种NARX神经网络辅助导航输出的导航轨迹，与方法一相比，方法二和方法三的航向角偏差较小，在GNSS失效初期运动轨迹基本与理想轨迹重叠，但在转弯后轨迹偏差较大。蓝色实线(方法四)为本文提出的一种NARX神经网络辅助导航方法，在该方法的辅助下输出的运动轨迹最贴近理想轨迹，从GNSS失效初期直至轨迹转弯前，方法四输出的轨迹基本与理想轨迹重叠，仅存在微小的航向角偏差，即使在转弯后，方法四输出的轨迹也紧贴理想轨迹。

不同方法组合导航位置和速度误差如图5和图6所示，为使误差曲线清晰简洁，并突出卫星失效期间组合导航误差的变化情况，这里仅给出1200～1500 s期间组合导航北向位置和速度误差对比曲线。

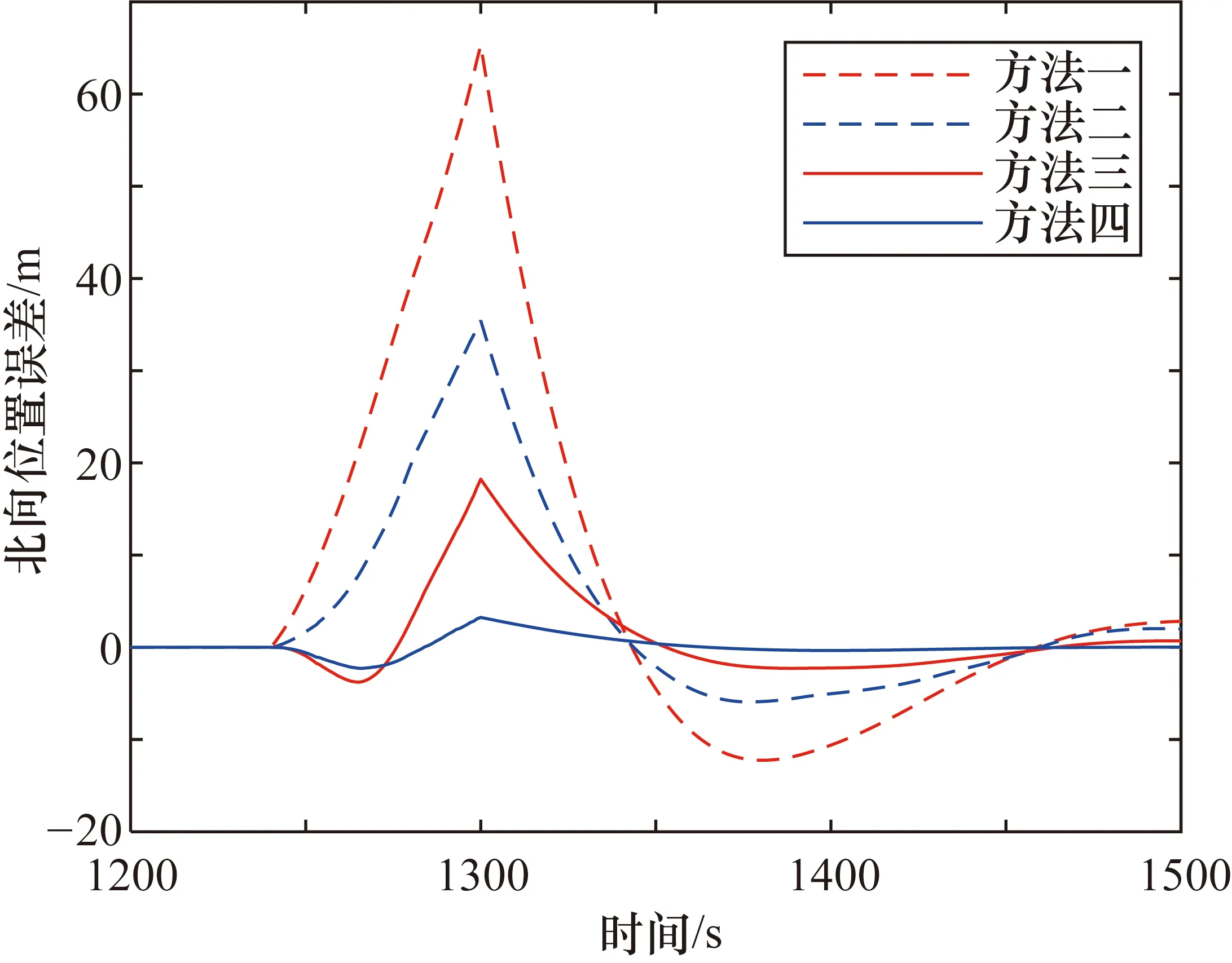
图5 组合导航位置误差

图6 组合导航速度误差

如图5和图6所示，不同方法的导航误差在1240 s GNSS失效后开始逐渐增大，其中方法一误差增速最大，方法四误差增长最缓慢。不同方法的导航误差均在1300 s左右达到最大值，方法一至方法四的最大北向位置误差分别是65 m、35 m、18 m、3.2 m，方法一至方法四的最大北向速度误差分别是1.3 m/s、0.65 m/s、0.44 m/s、0.1 m/s。尽管1300 s后GNSS恢复正常工作，受GNSS失效期间的影响，卡尔曼滤波出现短暂的震荡后才逐步恢复平稳。不同方法的误差曲线走势基本一致，在相同时间内方法一所达到的位置和速度误差最大，方法一误差曲线震荡最为剧烈。GNSS失效期间方法四位置和速度误差始终保持在较小的区间内，与其他方法相比，方法四误差曲线最为平缓。方法四在使用神经网络对组合导航系统进行辅助的基础上，尽可能地简化了神经网络的输入与输出的关系，使得神经网络更容易训练，能够较好地拟合输入输出关系，进而能够更大程度地减轻GNSS失效对组合导航系统的影响。不同导航方法的导航最大误差如表1所示，导航均方根误差如表2所示。

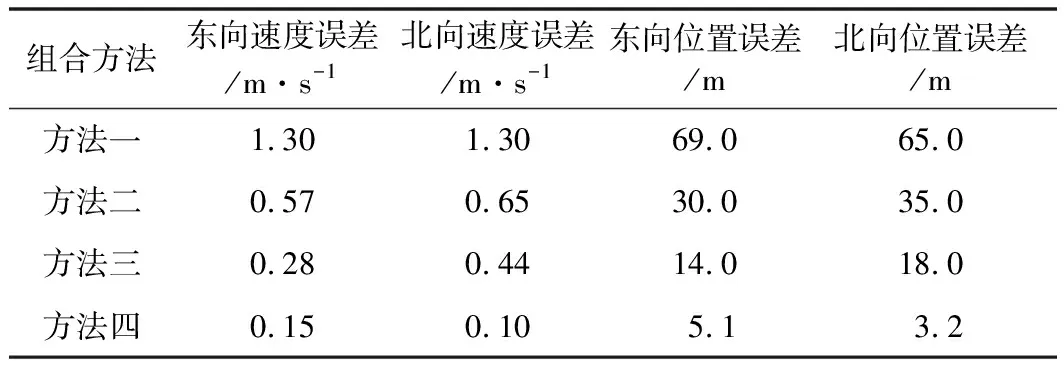
表1 组合导航最大误差表

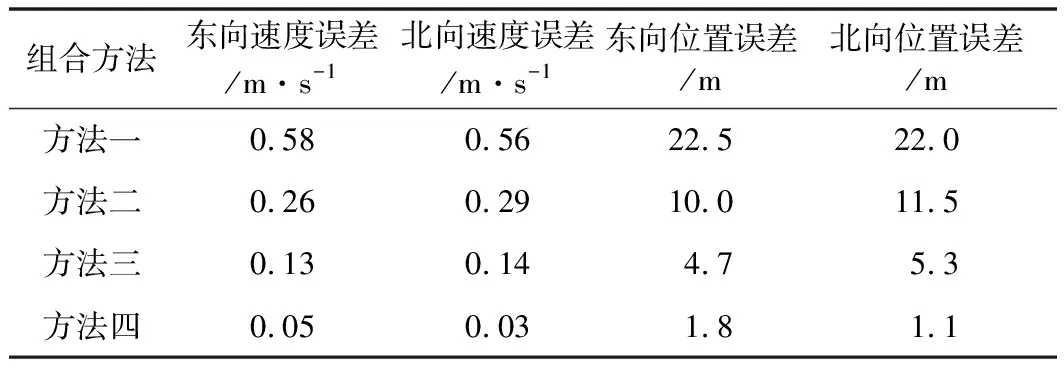
表2 组合导航均方根误差表

方法四与方法一的对比证明了提出的NARX神经网络辅助组合导航方法的有效性，根据导航均方根误差计算，方法四相较于方法一导航误差减小了约90%；方法四与方法二的对比证明了NARX神经网络相较于BP神经网络在辅助组合导航工作方面的优越性，根据导航均方根误差计算，方法四相较于方法二导航误差减小了约80%；方法四与方法三的对比证明了提出的NARX神经网络辅助组合导航方法与现有方法相比具有一定优势，根据导航均方根误差计算，方法四相较于方法三导航误差减小了约60%。GNSS失效60 s期间，方法四导航最大位置误差5.1 m、最大速度误差0.15 m/s，实验证明本文提出的NARX神经网络辅助的组合导航方法能够较好地消减短时GNSS失效对组合导航精度造成的影响。

5 结束语

针对短时GNSS失效会对工作在城市环境中车辆的导航精度造成很大影响的问题，提出了一种NARX神经网络辅助组合导航的方法。神经网络输入为惯性导航解算得到的位置速度增量和IMU输出的角速度和加速度信息，网络目标输出为GNSS位置速度增量。通过一组实测数据实验证明，所提出的NARX神经网络辅助组合导航的方法能够有效消减GNSS失效对组合导航系统造成的影响。神经网络在训练时易陷入局部最优解，减弱了神经网络对组合导航系统的辅助能力，可将神经网络训练方法的改进作为下一步研究内容。