三重降噪的盲源分离抗干扰算法*
曹 越,张 杭,朱宏鹏,李睿思,曹 静
(1.陆军工程大学 a.通信工程学院;b.指挥控制工程学院,南京 210007;2.中国人民解放军31108部队,南京 210016)
0 引 言
在目前复杂电磁环境中,卫星通信装备和系统面临的干扰威胁非常严重。为了有效解决抗干扰问题,盲源分离技术被应用于抗干扰通信,并取得了较好的效果[1-2]。但是卫星通信因传输距离远导致观测信号非常微弱,因此接收端的信噪比很低。同时,传统盲源分离算法的分离性能对于信噪比的强弱很敏感,导致低信噪比条件下会出现分离性能恶化。
目前,已有多种降噪技术应用于不同领域。针对经验模态分解(Empirical Mode Decomposition,EMD)的模态混叠现象,Wu等人[3]提出了一种基于噪声辅助分析的改进EMD方法,即集合经验模态分解(Ensemble Empirical Mode Decomposition,EEMD)。该方法需要多次加入不同的辅助白噪声,然后通过平均的方式消除引入噪声的影响,最终使分解过程具有抗噪特性。Yeh等人[4]进一步改进了EEMD方法,加入的辅助噪声采用正、负成对的形式,能够很好地消除重构信号中的残余辅助噪声,而且加入的噪声集合次数可以很低,计算效率较高,这种方法被称为互补集合经验模态分解(Complementary Ensemble Empirical Mode Decomposition,CEEMD)。
针对现有文献所提算法在采用EEMD时集合平均次数多、计算成本高、运算速度慢的问题,本文提出了一种基于CEEMD降噪、小波阈值降噪和随机共振(Stochastic Resonance,SR)降噪的三重降噪盲源分离抗干扰算法。仿真结果表明,本文所采用的互补集合经验模态分解降噪算法相比集合经验模态分解算法的计算量大大减少,并且本文所提三重降噪方案可有效改善低信噪比条件下盲源分离的性能。
1 降噪算法
1.1 互补集合经验模态分解降噪算法
CEEMD的步骤如下:
Step1 设定总体平均次数M。
Step2 在原始信号x(t)上加入数值大小相等,符号相反的两组标准正态分布的白噪声ni(t)和-ni(t),即
(1)
式中:ni(t)表示第i次加性高斯白噪声序列;xi+(t)和xi-(t)表示第i次加入正负白噪声后的含噪信号。
Step3 对xi+(t)和xi-(t)进行EMD分解,得到若干IMF(Intrinsic Mode Function)分量,即
(2)
式中:ci,j+(t)和ci,j-(t)分别为第i次加入正负高斯白噪声后分解得到的第j个IMF分量;ri,j+(t)和ri,j-(t)为EMD分解的残余分量;J是IMF的数量。
Step4 重复Step 2和Step 3M次,将上述对应的IMF进行集合平均运算,CEEMD分解得到的第j个IMF分量为
(3)
1.2 小波阈值降噪算法
小波阈值降噪因其在Besov空间上可得到最佳估计值[5],故选择小波阈值降噪对含噪观测信号x(t)进行消噪。在实际应用中,一般是按照某种方式将连续小波及其变换作离散化处理[6]。
文献[7-8]指出,一般小波阈值降噪的分解层数选择3层即可提高降噪效果。本文选取db4,3层分解对含噪信号进行小波阈值降噪。
1.3 双稳态随机共振降噪算法
从信号处理的角度来看,随机共振[9]是指利用输入信号、噪声和非线性系统之间产生的协同效应,将部分噪声能量转换为信号能量,实现增强信号和抑制噪声的现象。
随机共振中输入信号、噪声和非线性系统是基本要素。本文重点介绍最基本的非线性双稳态系统,其过程可用Langevin方程[10]表示:

(4)
式中:x(t)为随机共振系统输出信号;s(t)为系统输入信号;a和b为正数的系统参数;n(t)是均值为0、方差为σ2的加性高斯白噪声。
随机共振系统可以通过四阶Runge-Kutta算法[11]求解,具体迭代公式如下:
(5)
式中:xn、sn分别为输出信号x(t)和输入信号s(t)的第n次采样值;h为积分步长,在绝热近似小参数条件下h=1/fs。
2 基于三重降噪的盲源分离抗干扰方案
2.1 三重降噪的盲源分离抗干扰算法模型
本文提出的三重降噪模型如图1所示。经BPSK调制的基带通信信号在无线信道的传输过程中与多路干扰相混合,无线信道中固有的加性噪声使这种混合呈现含噪混合特性,即
x(t)=As(t)+n(t)。
(6)
式中:x(t)=[x1(t),x2(t),…,xM(t)]T表示观测信号向量;s(t)=[s1(t),J2(t),…,JN(t)]T表示未知源信号向量(包含一路通信信号和N-1路干扰,并假设其互相独立),s1(t)表示通信信号,Ji(t)表示干扰信号;n(t)=[n1(t),n2(t),…,nM(t)]T表示噪声信号向量;A表示M×N维混合矩阵,且为未知线性混合矩阵,表征了无线信道对通信信号和干扰信号在传输过程中的混合状态,N为源信号个数,M为观测信号个数。


图1 三重降噪的盲源分离抗干扰算法模型
2.2 实现方案
2.2.1 “小波阈值降噪+CEEMD降噪”的前降噪方案
这是一种先进行小波阈值降噪再进行CEEMD降噪的前降噪方案,如图2所示。

图2 “小波阈值降噪+CEEMD降噪”前降噪方案
为保证降噪算法的稳定性,先对观测信号x(t)进行小波阈值降噪处理,充分利用小波阈值降噪算法降噪性能的稳定性特点,消除部分噪声,减小下一步CEEMD分解时产生的累积误差,从而减少CEEMD中加入成对的正负高斯白噪声的次数,提高分解质量以及降低运算量。利用CEEMD算法进行二次降噪,进一步提高观测信号信噪比,其具体步骤如下:
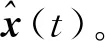
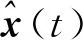
(7)
式中:k为噪声IMF的分量个数。
2.2.2 “CEEMD降噪+小波阈值降噪”的前降噪方案
这是一种先进行CEEMD降噪再进行小波阈值降噪的前降噪方案,如图3所示。

图3 “CEEMD降噪+小波阈值降噪”前降噪方案
CEEMD在原始信号中加入正负成对的辅助白噪声并在集合平均时相互抵消,提高了分解效率。同时保留原始信号的非线性与非平稳性等特征,降低集总平均次数,重构后的信号噪声明显减少。因此,利用CEEMD降噪,对观测信号x(t)进行第一次降噪,为小波阈值降噪在较高信噪比条件下工作创造条件,然后对信号进行小波二次降噪,使得降噪效果更加显著。其具体步骤如下:
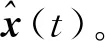
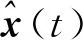
2.2.3 “CEEMD降噪与小波阈值降噪融合”的前降噪方案
这是一种对CEEMD各IMF分量进行小波阈值降噪的前降噪方案,如图4所示。

图4 “CEEMD降噪与小波阈值降噪相融合”的前降噪方案示意图

3 仿真与性能分析
仿真的混合场景为两发两收的线性瞬时适定混合,分离算法采用基于独立性的等变自适应分离(Equivariant Adaptive Separation via Independence,EASI)算法[12]。
为验证本文提出的算法,仿真分析本算法在不同信噪比、不同信干比和不同干扰样式条件下的相关系数性能。仿真参数的设定如表1所示。
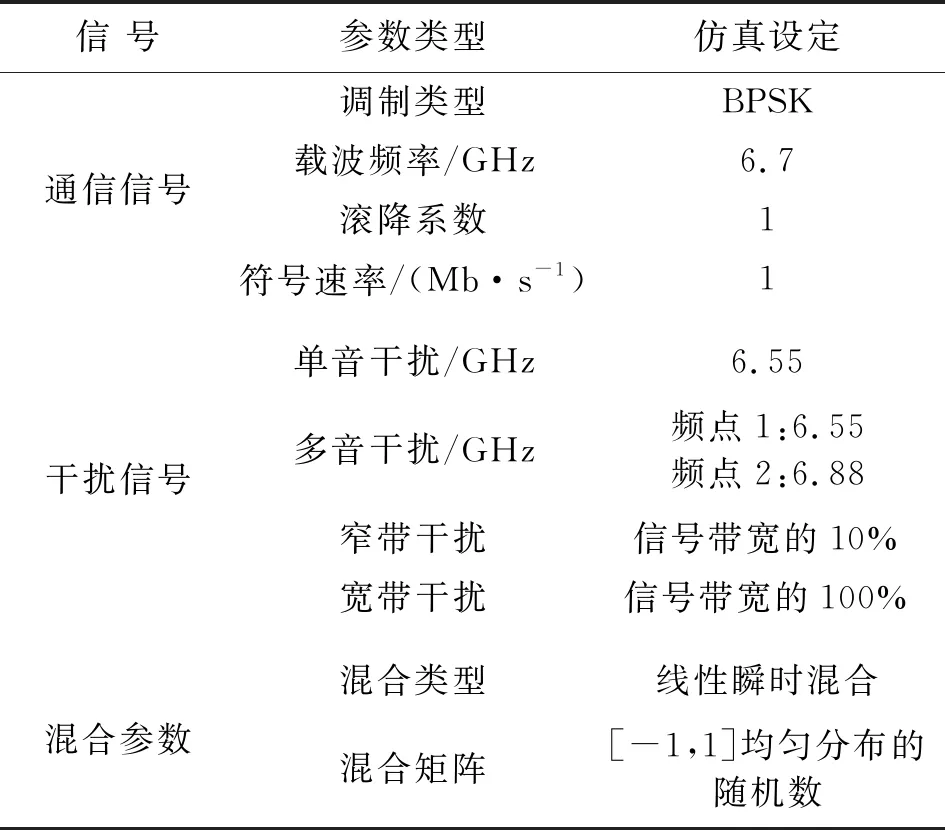
表1 仿真参数
3.1 衡量分离性能的指标
本文采用相似系数(Similarity Coefficient)[13]作为盲源分离评价指标。该指标是衡量分离信号与源信号相似程度的物理量,其定义为
(8)
式中:yi(k)表示第i个分离信号;sj(k)表示第j个源信号;L表示样本长度;ρij表示第i个分离信号和第j个源信号的相似程度,当完全分离时ρij趋近于1。
3.2 直接序列扩频对后降噪性能的影响
为验证直接序列扩频对后降噪性能的影响,本文在单音干扰、多音干扰、窄带干扰以及宽带干扰在0 dB信干比条件下,选择“小波阈值降噪+CEEMD降噪”的前降噪方案,对有无扩频情况下的后降噪效果进行仿真。此处源信号为图1中的y(t),扩频后降噪分离信号以及未经扩频的后降噪分离信号在不同信噪比条件下的相似系数仿真结果如图5所示。
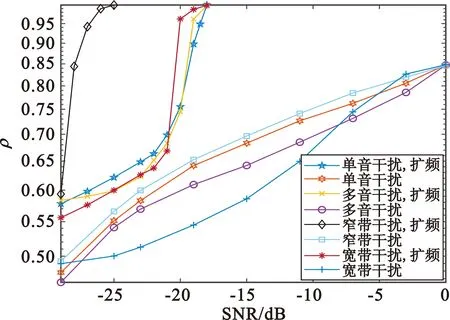
图5 不同干扰下扩频对后降噪性能的影响
由仿真结果可知,相较于直接采用随机共振算法对分离信号做后降噪处理,经过直接序列扩频后再采用随机共振算法进行降噪,而后进行解扩,对分离信号的降噪效果更好;在相同信噪比条件下,相似系数远高于未经扩频的后降噪处理,有利于改善盲源分离算法在低信噪比情况下的分离精度。
3.3 信噪比对分离性能的影响
由于盲源分离的性能决定了干扰消除的能力,而盲源分离的性能又受信噪比的影响,所以本文在一定信干比条件下考察信噪比对盲源分离性能的影响。
固定信干比,调整信噪比,对单音干扰、多音干扰、窄带干扰以及宽带干扰经不同前降噪方案在0 dB和-15 dB信干比条件下的分离性能进行仿真,结果如图6和图7所示。

(a)单音干扰

(b)多音干扰

(c)窄带干扰
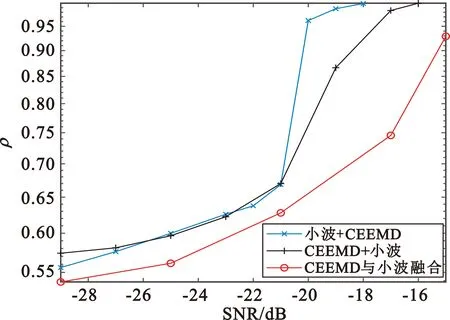
(d)宽带干扰图6 SIR=0 dB时信噪比对不同前降噪方案的分离性能的影响

(a)单音干扰
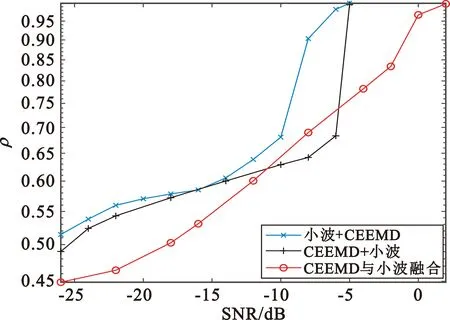
(b)多音干扰
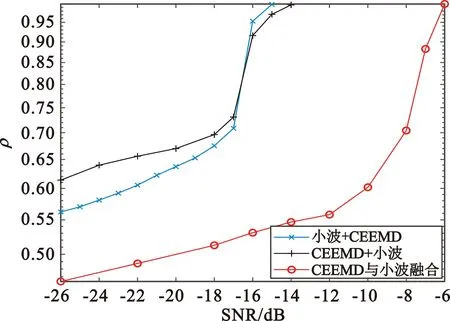
(d)宽带干扰图7 SIR=-15 dB时信噪比对不同前降噪方案的分离性能的影响
由仿真结果可知,信干比为0 dB时,针对四种干扰类型,采用“小波阈值降噪+CEEMD降噪”的前降噪方案的联合降噪算法均具有最好的分离性能。“小波阈值降噪+CEEMD降噪”前降噪方案至少可以在信噪比为-17 dB情况下使得信号解调后的相似系数达到0.99以上;“CEEMD降噪+小波阈值降噪”前降噪方案则至少可以在信噪比为-15 dB情况下使得信号解调后的相似系数达到0.99以上;“CEEMD降噪与小波阈值降噪融合”的前降噪方案性能稍逊于上述两种前降噪方案,该方案至少可以在信噪比为-11 dB时方可使得信号解调后的相似系数达到0.99以上。
信干比为-15 dB时,针对四种干扰类型,采用“小波阈值降噪+CEEMD”的前降噪方案和采用“CEEMD降噪+小波阈值降噪”前降噪方案的联合降噪算法的分离性能相似,均至少可以在信噪比为-4 dB情况下使得信号解调后的相似系数达到0.99以上;“CEEMD降噪与小波阈值降噪融合”的前降噪方案性能弱于上述两种前降噪方案,该方案至少可以在信噪比为6 dB时方可使得信号解调后的相似系数达到0.99以上。
3.4 信干比对分离性能的影响
考察一定信噪比条件下,本文所提算法模型(如图1所示)的抗干扰性能。调整信干比,将单音干扰、多音干扰、窄带干扰以及宽带干扰在0 dB和-15 dB信噪比条件下的分离性能进行仿真,结果如图8和图9所示。
由图8的仿真结果可知,信噪比为0 dB时,针对四种干扰类型,采用“小波阈值降噪+CEEMD降噪”的前降噪方案的联合降噪算法均具有最好的分离性能。“小波阈值降噪+CEEMD降噪”前降噪方案至少可以在信干比为-18 dB情况下使得信号解调后的相似系数达到0.99以上;“CEEMD降噪+小波阈值降噪”前降噪方案则至少可以在信干比为-17 dB情况下使得信号解调后的相似系数达到0.99以上;“CEEMD降噪与小波阈值降噪融合”的前降噪方案性能稍逊于上述两种前降噪方案,该方案至少可以在信干比为-11 dB时方可使得信号解调后的相似系数达到0.99以上。
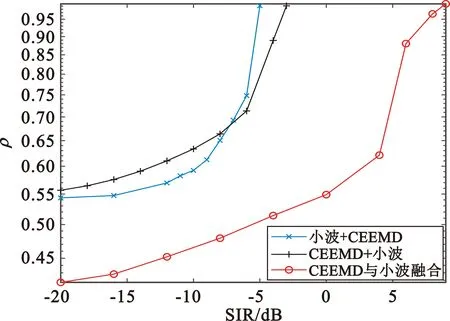
信噪比为-15 dB时,针对四种干扰类型,采用“小波阈值降噪+CEEMD降噪”的前降噪方案的联合降噪算法均具有最好的分离性能。“小波阈值降噪+CEEMD降噪”前降噪方案至少可以在信干比为-4 dB情况下使得信号解调后的相似系数达到0.99以上;“CEEMD降噪+小波阈值降噪”前降噪方案则至少可以在信干比为-3 dB情况下使得信号解调后的相似系数达到0.99以上;“CEEMD降噪与小波阈值降噪融合”的前降噪方案性能稍逊于上述两种前降噪方案,该方案至少可以在信干比为10 dB时方可使得信号解调后的相似系数达到0.99以上。
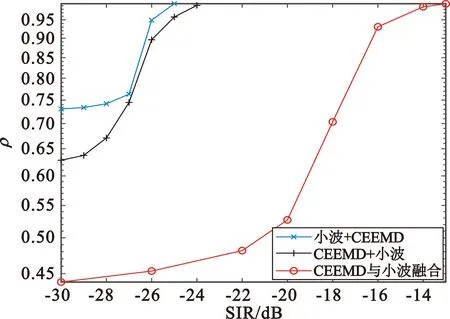
(a)单音干扰

(b)多音干扰
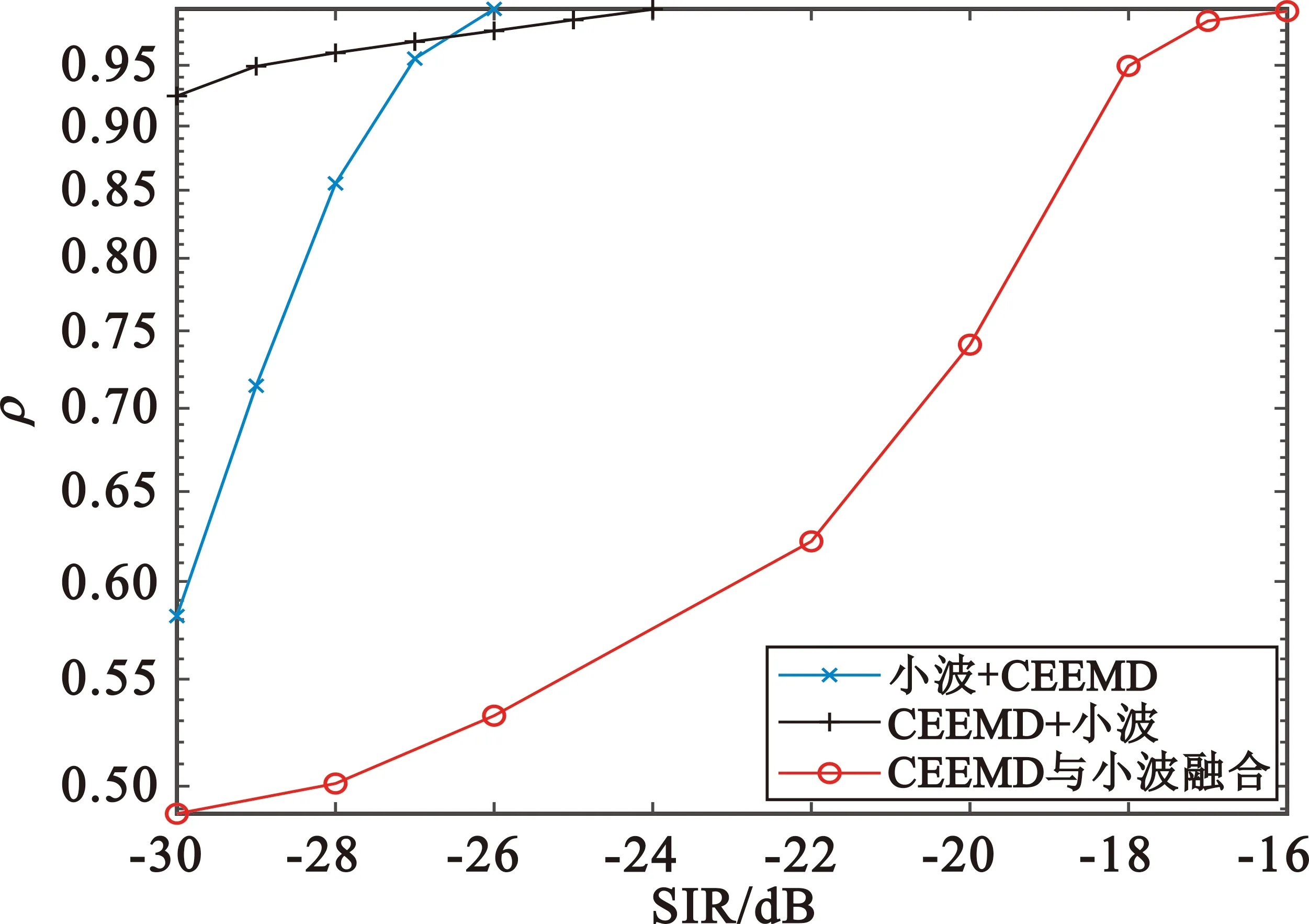
(c)窄带干扰
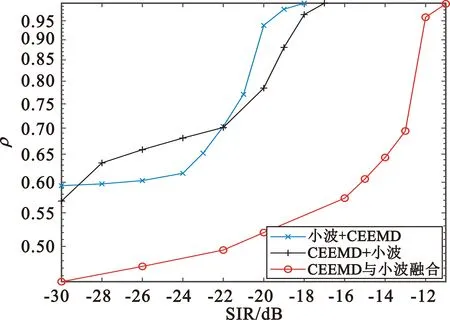
(d)宽带干扰图8 SNR=0 dB时信干比对不同前降噪方案的分离性能的影响
(a)单音干扰

(b)多音干扰

(c)窄带干扰
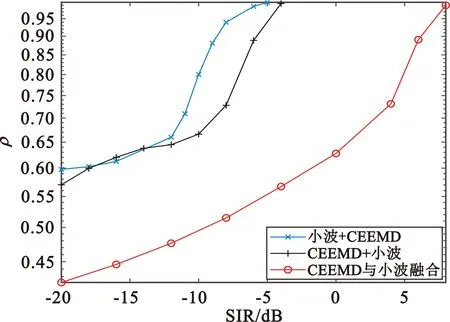
(d)宽带干扰图9 SNR=-15 dB时信干比对不同前降噪方案的分离性能的影响
4 结 论
本文提出了一种基于三重降噪的盲源分离抗干扰算法,重点解决低信噪比条件下盲源分离算法性能恶化的问题。仿真结果显示,采用的CEEMD降噪算法相比EEMD降噪算法的计算量大大减少,采用“小波阈值降噪降噪+CEEMD降噪”的前降噪方案相较于其他两种方案的算法性能更好。本文所提算法可用于因信号微弱导致接收信噪比低的卫星通信系统,同时不需要占用额外频带资源,可进一步提升其干扰容限,有利于提高通信系统的抗干扰能力,具有较大的应用潜力。

