船舶岸电的应用与研究

山东理工大学 高月昊 贾明娜

1 船舶岸电国内外应用现状

1.1 PQ控制原理分析

PQ控制又称恒功率控制。其控制主要目的是使输出的有功和无功功率跟踪其参考值功率，岸电并网的频率和电压由大电网支撑。PQ控制可有效保证发电功率输出的稳定，使敏感负荷和重要负荷免于干扰，确保系统正常运行。

从图1可看出，当岸电电源的频率在允许的范围内（fmin≤f≤fmax）变化时，逆变器输出的有功功率维持在给定的参考值Pref；当岸电电源的电压幅值在允许的范围内（Vmin≤V≤Vmax）变化时，逆变器输出的无功功率维持在给定的参考值Qref。岸电电源采用PQ控制的逆变器的主电路为三相全桥电路，逆变器输出采用LC滤波器。控制部分包括功率控制模块、电流控制模块、锁相环(PLL)、相位预同步模块和PWM调制模块。电流环PI控制器可实现对指定电流值的跟踪，达到无静差控制的效果，电流环的等效图如图2。

图1 PQ控制原理图

图2 电流内环控制框图

1.2 PR和QPR控制原理分析

PR控制是由Garcia和Morari在二十世纪八十年代提出的内模原理的应用。内模原理一个典型应用就是工程上最常用的PI控制器中的积分环节。内模原理是将某一频率对应的指令信号的模型加入到控制系统中，则加入后的控制系统对于这一频率有无穷大的增益、能对此频率实现无静差跟踪，而对于其它频率增益很小，没有跟踪效果。PR控制器数学理论基础虽然早在二十世纪就已提出，但在有源滤波器中使用的时间并不长，近年PR控制器大量应用于并网逆变器入网电流控制当中。

其传递函数为：GPR(s)=Kp+2Krs/(s+ω02)，这其中：Kp和Kr分别为比例环节和积分环节的系数。当给定交流信号的角频率为ω0时，将s=jω0代入上式得到PR控制器在此频率处的增益为：GPR(jω0)=Kp+2Krω0/((jω0)2+ω02)=∞。

虽然PR控制器性能优异，但现实中电网的频率会发生轻微偏移。PR控制器对于指定次频率增益无限大，但对指定频率附近其他频率几乎没有増益。当电网频率发生偏移PR控制器的控制效果大打折扣，因此准比例谐振控制器（QPR）产生了，它能有效增加指定谐振频率附近的频率的増益，防止系统频率波动时无法实现良好的控制。

在PR控制器的jω轴上加入两个频率固定不变的闭环极点，即构成准比例谐振控制器（QPR），传递函数为：GQPR(s)=Kp+2Krωcs/(s2+2ωcs+ω02)。其中：ω0为指定次谐波频率，ωc为截止频率。当给定交流信号的角频率为ω0时，将s=jω0代入上式得到QPR控制器在此频率处的增益为：GQPR(jω0)=Kp+2Krωcjω0/((jω0)2+2ωcjω0+ω02)。

准比例谐振控制器在指定次谐波处增益虽不是无穷大，但也能满足指定次频率的控制要求，通过调节Kr还能调节带宽，适当增加带宽能抵消频率波动带来的影响，其控制框图如图3。

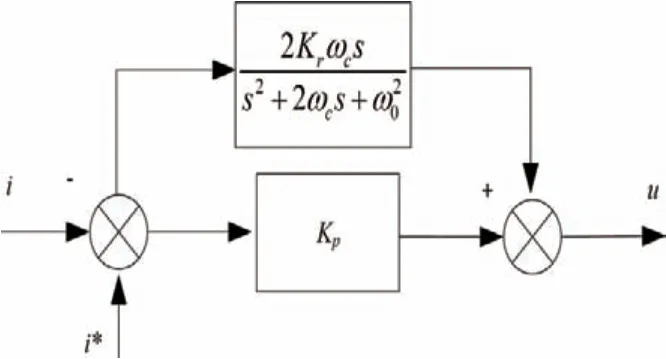
图3 QPR电流控制器的控制框图

由QPR控制器传递函数GQPR(s)可看出，影响控制器性能的参数有Kp、Kr和ωc，因此可通过控制变量法选取几组参数进行对比分析，确定各参数对各个控制器的影响。不同参数时PI、PR与QPR控制器控制参数Kp增大而其他参数不变时，QPR控制器低频和高频位置幅值均增大，相应的相位裕度也变大；控制参数Kr增大而其他参数不变时，QPR控制器峰值增益变大；控制参数ωc增大则控制器带宽明显变大，ωc参数影响控制器带宽大小。据此分析可知，根据系统峰值增益需求可选择较大的Kr和ωc值，使系统获得较大的峰值增益、减小基频处的稳态误差，同时系统获得较大的带宽可更好地适应电网频率变化，保证系统稳定性。

2 基于重复+QPR的船舶岸电并网控制

为实现并网电流的无静差控制，引入重复控制策略、并与QPR控制相配合，以期提高LCL型并网逆变器的输出控制性能[1-2]。

2.1 重复控制原理分析

基于内模原理的重复控制器，可有效地消除控制系统内周期性的扰动和误差，主要应用于输入为周期性信号的系统，这与并网逆变器的给定和扰动量皆为正弦信号的特性相契合。因此，选择重复控制作为并网逆变器输出电流的跟踪策略。

图4 重复控制器内模结构图

在离散域下传递函数为：G(s)=1/(1-Q(s)Z-N)，式中：N为一个基波周期的采样次数，Q为内模系数。为提高重复控制器自身的稳定性，Q通常取值为略小于1的常数，或者为增益小于1的低通滤波器。但Q并不是越小越好，不同的Q对系统的影响不同。重复控制在基波频率和基波倍数频率处具有高增益和零相移特性，Q越大幅值处增益越大，系统稳态精度越高，但稳定性越差；Q越小幅值处增益越小，控制精度较差，但稳定性较强。

根据稳定性判据和重复控制的频率特性可知，G(s)本身不存在稳定性问题。但如直接将其应用于逆变器的电流控制，则由于LCL滤波器的原因将导致系统的相频特性曲线穿越负180°，带来稳定性问题。因此在实际的应用中，除内模环节，重复控制器还包括延迟环节Z-N和补偿器M(s)。从图5可见，重复控制属延时控制，其中包含的延时环节使其输出的动态性能较差，因此将重复控制与其他控制方法进行组合互补，效果最佳。

图5 重复控制器结构图

2.2 基于重复+QPR的并网逆变器控制

在控制原理的基础上引入重复控制策略；同时为提高系统的动态性能，将指令电流前馈至QPR控制器。基于重复+QPR控制的LCL型并网逆变器控制原理如图6所示,其中Grep为重复控制器的传递函数。在此基础上，可设计基于重复+QPR控制的PQ控制器（图7），据此绘制出重复+QPR控制系统的结构框图。

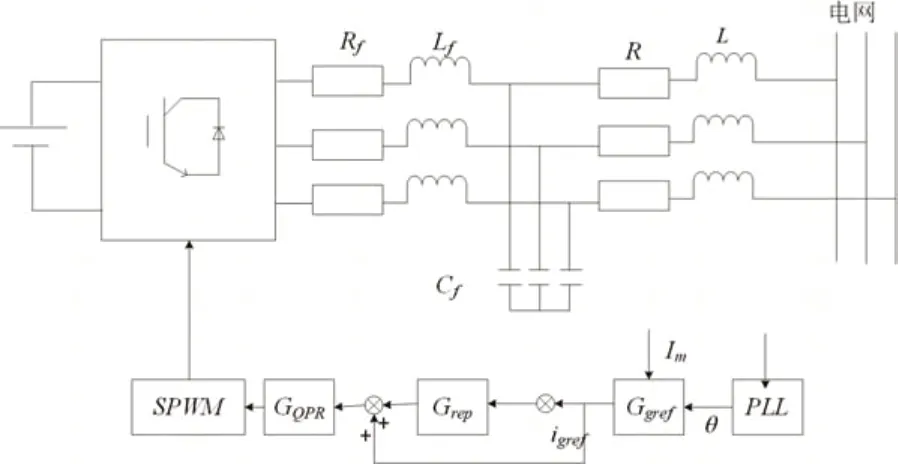
图6 重复+QPR控制原理图

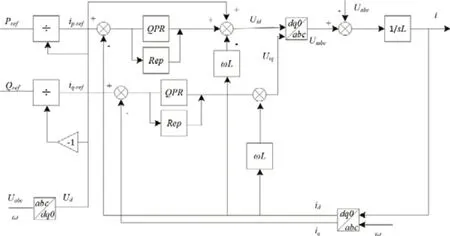
图7 基于重复+QPR控制的PQ控制器结构图

图8展现了内外环间的结构关系：QPR控制作为内环，结合并网电流反馈，增加系统阻尼；重复控制作为外环实现对并网电流Ig的无静差跟踪。同时，将重复控制器的输出信号与指令电流信号Igref叠加作为QPR控制器的输入信号，以期在指令电流改变时瞬时值反馈内环能快速响应前馈电流指令，消除重复控制的固有一周期延时，提高整个系统的动态响应能力。

图8 重复+QPR控制系统框图

3 仿真分析

重复+QPR控制策略用于并网系统中，根据对重复+QPR控制策略的分析，在Matlab／Simu_link环境下建立PQ控制下基于重复+QPR的电流内环仿真模型图。设定总仿真时间为0.5s，仿真中0到0.25s之间发电输出有功功率为Pref=10kW，无功功率为Qref=0kVar；0.25s至0.5s之间发电输出有功功率为Pref=15kW，无功功率为Qref=6.5kVar。为提高仿真速度，岸电电源用650V直流电压源代替，负荷容量为500kW恒功率负荷，微电网三相交流电压相电压值为380V。电流PI调节器参数设定为Kp=800、Kr=800、Wc=100，滤波器参数设定为R=0.01Ω、L=0.009H、C=110μF， 采 用SPWM调制。

图9中，上方为有功功率输出、下方为无功功率输出。可看出，PQ控制下采用重复+QPR控制不仅能有效控制发电的有功和无功输出，还可使得有功和无功功率都能更好地跟踪给定参考值，系统运行更加稳定，响应速度更快，控制性能更好。

图9 PQ控制下基于重复+QPR的仿真波形图