斜拉桥斜塔锚固区环形预应力孔道摩阻试验研究

刘壮武 LIU Zhuang-wu；章晨昊 ZHANG Chen-hao

（山东交通学院，济南 250300）

0 引言

为检验桥梁索塔设计所取计算参数的准确性，避免得到的预应力损失存在过大差异，更精确地得到张拉的控制应力和预应力筋伸长量，对其进行摩阻试验测试是直接且必要的办法。

1 工程概况

某斜拉桥工程主桥全长328m，为（90+238）m独塔、斜塔中央索面混合梁斜拉桥，结构总体为塔、墩、梁固结体系。斜拉桥主塔混凝土为C50混凝土，以U型钢束作为索塔锚固区的配置，两端使用并行同步张拉的施工工艺，其管道是镀锌的金属波纹管、且使用真空辅助压浆工艺。

第一次试验截面高程为262.495m，位于桥塔19节段，锚块编号MK1，环向预应力筋编号N4预应力束，截面尺寸为顺桥向7.545m，横桥向9.002m，锚固于塔柱内侧，如图1所示，其预应力钢束规格为Φ15.2-19，环向曲率半径R为1.8m，钢绞线公称直径d为15.2mm，公称面积A为139mm2，标准强度为1860MPa，弹性模量Ep=1.95×105MPa，张拉控制应力为0.75fpk，锚固于塔柱外侧。索塔内部的预应力钢束采用U形预应力钢绞线束，其具体布置如图1所示，试验时塔柱混凝土的实际立方强度达到设计强度等级值的80%以后张拉钢束，U型预应力钢束采用两端张拉，Pk=3684.195KN，初始张拉吨位按10%的设计张拉力，从初张拉应力到张拉控制应力分别为0.2Pk、0.4Pk、0.6Pk、0.8Pk、1.0Pk逐级增压张拉。每级持载时间为2min，末级为5min。如图1所示。

第二次试验截面高程为279.495m，位于桥塔23节段，锚块编号MK6，环向预应力筋编号N1预应力束，截面尺寸为顺桥向7.381m，横桥向7.564m，锚固于塔柱外侧，如图2所示。其预应力钢束规格同为Φ15.2-19，钢束规格为Φ15.2-19，环向曲率半径R为1.8m，钢绞线公称直径d为15.2mm，公称面积A为139mm2，标准强度为1860MPa，弹性模量Ep=1.95×105MPa，张拉控制应力为0.75fpk，锚固于塔柱外侧。索塔内部的预应力钢束采用U形预应力钢绞线束，其具体布置如图3所示，试验时塔柱混凝土的实际立方强度达到设计强度等级值的80%以后张拉钢束，U型预应力钢束采用两端张拉，Pk=3684.195kN，初始张拉吨位按10%的设计张拉力，从初张拉应力到张拉控制应力分别为0.2Pk、0.4Pk、0.6Pk、0.8Pk、1.0Pk五级。每级持载2min，末级持载5min。如图2所示。

2 试验方法

为准确得到索塔内部管道部分的摩阻试验测试数据，通过压力传感器测量得到张拉主动端和被动端的压力，摒弃千斤顶油压表读取数据的方式，采用原理如图4所示的装置进行试验，因为千斤顶和索塔或工具锚相互直接受力，故而压缩变形等各种外界不利因素可以在张拉中得到及时的补偿更改，而且测试的耗时比较短，免除了收缩与徐变等外界因素造成的不利影响，所以测得的两端压力传感器读数的差值即是孔道的摩阻损失。如图4所示。

3 操作流程

①将预应力钢束穿过孔道，保证所有钢束进出管道的位置保持相同，避免其交叉或扭缠；

②在预应力筋的两端各装1台千斤顶同时充油保持一定数值（约4MPa），试验时采用单端张拉，测试时首先将两端千斤顶的油缸升压，使预应力钢索的张拉应力达到初张拉应力值0.1σcon，稳住油压，并将回油阀关死；记录两端读数（油压表压力、压力传感器和千斤顶活塞伸长值）；

③开动张拉主动端千斤顶进行张拉，从初张拉到张拉控制应力分级为0.2Pk、0.4Pk、0.6Pk、0.8Pk、1.0Pk五级。每级持荷2min，末级为5min。记录两端各项指标读数；

④当张拉拉力到设计值时，逐步回油到零，按以上步骤再进行2次；然后主被动端互换，上述过程继续重复3次；

⑤计算两端张拉力差值即为该孔道的摩阻损失。

4 试验数据处理分析

4.1 由管道摩阻所产生的应力损失

σL=σcon[1-e-（μθ+tx）]

σcon——锚下控制张拉应力；

μ——预应力孔道摩阻系数；

θ——从张拉端至计算截面曲线孔道部分切线夹角，rad；

t——管道相对于其设计位置偏差的系数；

x——从张拉端至计算截面孔道长度，m。

设主动端的张拉力值为P1，被动端的张拉力值为P2，则公式两边同时乘以预应力钢束的有效面积可得：

张拉进程的孔道摩阻损失率为：

损失率=（P1-P2）/P1×100%

孔道偏差系数k根据施工规范取值，全U型孔道θ取3.14（即180°），根据工程实际计算x取值。

4.2 二元线性回归法计算μ、k值

分级测试预应力束张拉过程中主动端与被动端的荷载，并通过线性回归确定管道被动端和主动端荷载的比值，然后利用二元线性回归的方法确定预应力管道的μ、k值。

计算公式为：

式中：

Ci——第i个管道对应的值Ci=-ln（P2/P1），P1、P2分别为主动端与被动端传感器压力；

li——第i个管道对应力筋的水平投影长度（m）；

θi——第i个管道对应力筋的空间曲线包角（rad），曲线包角的实用计算以综合法的计算精度较好，其表达式为：

式中：

θH——空间曲线在水平面内投影的切线角之和；

θV——空间曲线在圆柱面内展开的竖向切线角之和；

n——实际测试的管道数目，且不同线形的力筋数目不小于2；

μ——钢筋与管道壁间的摩擦系数；

k——管道每米局部偏差对摩擦的影响系数。

二元线性回归法在使用过程中，其原始数据离散过大会导致计算得到的结果不稳定性增大，任意增减几组数据将会导致得到的结果发生大幅变化，故而该方法只有在原始数据稳定性较高的情况下才适用。

4.3 假定k值法原理

本试验中的预应力钢束长度不足20m，预应力管道x值也较小。第一次试验x取值为19.808m，第二次试验x取值为17.056m，规范中对管道每米局部偏差对摩擦的影响系数k给定值为0.0015，上式中“kx”，项数值应该很小。因此，分析试验结果时可让k值在0.0015左右浮动计算μ值，确定摩擦系数的取值。如表1所示。

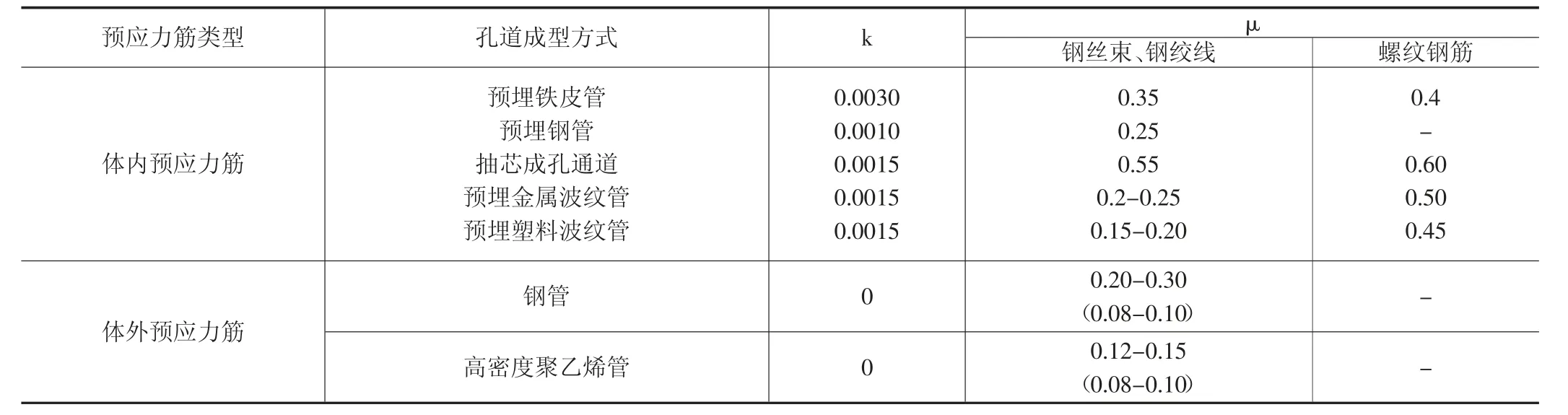
表1 公路桥涵施工技术规范对μ和k值取值规定

摩阻实验现场作业照，如图5所示。

5 结束语

本试验以宜昌市某斜拉桥为背景，利用实测数据，假定k值法求μ值，当k值取0.0015时，μ值均小于0.25，若假定μ值为0.25，k值均为负值，满足要求。同时当μ取0.0015，μ取0.25时，利用上述公式计算被动端/主动端的比值，即为最危险状态比值，得出第一次试验比值为0.442，第二次试验比值为0.4445，对照试验实测结果，比值均满足要求。

但是需要注意的是第一次孔道摩阻试验中，虽然μ和k值满足要求，但是施工方所使用的千斤顶加载力与理论加载力之间误差较大，这就要求施工单位在实际张拉过程中按误差情况进行适当补张，同时施工单位工程施工中应及时进行千斤顶标定，控制张拉误差，提高施工精度，确保索塔环向预应力按照设计理论值张拉到位。