Pb-Sn合金及Pb的热力学性质的第一性原理计算

刘伟歧， 强伟荣， 黄 整

(1. 西南交通大学希望学院， 成都 610400; 2. 西南交通大学 物理科学与技术学院， 成都 610031)

1 引 言

近年来，在热力学性质的基础研究方面，尤其是熔化温度机理更是引起高度重视. 由于物质的各异性、复杂性，对于探索不同压强下的熔化温度的统一机理却带来巨大的挑战，在理论方面更是困难重重. 因此研究过渡金属合金的熔化温度机理无疑是一个非常重要的课题.

Pb-Sn合金在工业、航空、军事等领域有着重要的用途及作用，尤其是在不同压强下的熔化温度机理研究引起科学研究者们的热门课题. 常压下合金中Pb的成分大约为62%时，其熔化温度也就是共晶温度大约为183 ℃[1]. Zhou等人[2]用改进的HPDTA实验方法得到了Pb (60﹪)-Sn(40﹪)合金, 在0-2.5 GPa范围内的熔化温度，表明大约压强达到1.16 GPa时其合金保持共晶熔化关系，此时1.16 GPa的共晶温度为220 ℃，而高于1.16 GPa时，出现了分叉的现象，E Yu Tonk等认为是Pb在Sn的BCT结构中的固溶现象. Rao等人[3]用快速增压法研究了Pb-Sn合金在不同组分比例下的晶格参数，通过比较表明合金中Sn的增加使得Pb的晶格参数逐渐减小 (其中变化率为0.0139 nm/at%Sn)，越小的晶格参数值说明了有更高的过饱和铅相. 而过渡元素Pb单质，在常温常压下其晶格结构为面心结构，晶格参数为0.49502 nm[4]，熔点为327 ℃[1].

对于Pb-Sn合金熔化温度的研究大多采用实验方法[5-13]，而基于理论研究[14]的报道却鲜少. 本文基于第一性原理的ABINIT软件包，采用密度泛函理论(DFT)以及密度泛函微扰理论(DPFT)方法，相互关联势采用局域密度近似(LDA)，利用虚晶近似的计算手段优化计算了以Pb为基加入Sn的Pb (60﹪)-Sn(40﹪)合金的晶格参数、能量、电子能带以及态密度、声子色散结构以及态密度. 然后利用已得到的声子态密度，计算得到Pb-Sn合金在标准条件下(298.5 K，1 atm)热熔、熵、自由能以及内能. 采用本人已做的结果[15]中直接利用晶格之间的能量差可与达到熔化温度时的振动能量相当的固-液相变机理，得到Pb-Sn合金在标准压强下的熔化温度Tm，并与实验结果进行了对比. 同时与计算出Pb的热力学性质的结果进行了比较.

2 计算方法

本文计算以Pb为基加入Sn的Pb (60﹪)-Sn(40﹪)混合比例并采用虚晶近似方法，以及结合Trouiller-Martins-type局域密度近似(LDA)的赝势理论，通过优化计算Brillouin区K点取为6×6×6 ，平面波的截断能为707.51 eV 以保证计算的收敛性. Pb 采用Trouiller-Martins-type局域密度近似(LDA)的赝势理论的密度泛函理论方法，Brillouin区K格取为4×4×4，平面波的截断能取为435.38 eV，其中Pb原子的外层价电子组态为6s26p2.

3 计算结果与讨论

3.1 晶体结构

为了考察晶格能量的特征，令晶格参数a=b=c，a = b = g. 原胞的三个基矢分别为(x，0.5，0.5)，(0.5，x，0.5)，(0.5，0.5，x)，其中原胞参数x= 0，-0.25，-0.5时所对应的晶格结构分别为面心立方结构(FCC)，简单立方结构(SC)和体心立方结构(BCC).

首先，通过分别优化计算可得Pb-Sn合金的晶胞参数a为0.48347 nm，Pb的晶胞参数a为0.49872 nm，其比试验结果0.49502 nm[4]大0.7%. 通过比较Pb-Sn合金的晶胞参数比Pb的晶胞参数大0.01525 nm，这也说明了由于Sn的加入导致了铅的晶胞参数的变小，符合Rao等人[3]的描述.

其次，根据上述结果分别可得Pb-Sn合金及Pb的晶格能量与原胞参数x的变化关系(如图1所示). 可以看出，Pb-Sn合金在x= 0处晶格结构能量最低，即FCC为最稳定结构，其极高点为x= -0.35处所对应着的斜方结构而并非SC，二者的晶格能量差为0.0128 eV. 同时对比Pb晶格能量与原胞参数x的变化关系(如图2所示)，两者变化形状甚是相似. 只不过在所计算结果中，金属Pb在x= -0.5处(即BCC)的晶格能量稍低于x= 0处(FCC)的晶格能量0.01244 eV，比极高点x= -0.31低0.18932 eV.

图1 Pb-Sn合金的晶格能量与x的关系

图2 金属Pb的晶格能量与x的关系

3.2 电子能带

图3为计算所得的Pb-Sn合金的电子能带和态密度. 在费米面附近，有价带穿越费米面，形成范围较窄的导带，表现出一定的金属性. 在费米面上方3.3 eV～18.1 eV 和费米面下方-3.7 eV～-17.3 eV范围内，电子能带分布比较密. 且在16.1 eV和-8.3 eV处形成两个较大的态密度峰，主要是来Pb和Sn的s、p轨道贡献. 在对称点Gama、X、L等处，出现电子能带的交叠.

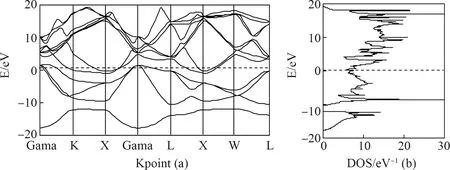
图3 Pb-Sn合金电子能带与态密度

对比计算所得Pb的电子能带和态密度(如图4所示)，二者的能带轮廓十分相似. 除了Pb在费米面上下所形成的两个态密度峰分别在4.1 eV和-6.6 eV，这说明Pb-Sn合金的电子能带的密集性较Pb的更趋向于远离费米面.

图4 金属Pb的电子能带与态密度

3.2 声子能带

图5所示为Pb-Sn的声子能带和态密度. 声子能带由三个声学波带构成，即一个纵声学(LA)波带和两个横声学(TA)波带. 其中LA的峰在79 cm-1处，TA的峰在44 cm-1处，总体上LA的能量高于TA的能量.

图5 Pb-Sn合金的声子能带与态密度

图6所示为Pb的声子能带和态密度并与实验值[16]作了对比，除了在X-Gama和Gama-L区间中理论所计算的TA分别较实验值稍有偏差外，其他区间的声子波带与实验值基本符合. 其LA峰值在69 cm-1处，TA峰值在44 cm-1处.

图6 Pb的声子能带与态密度

通过比较两者的声子能带可知，Pb-Sn合金的声学波带仅在X-Gama区间范围内LA和TA的能带部分相交叠且TA是二重简并的，而其它区间简并消失，且横声学波带有着明显的软化现象. 这表明随着金属锡的逐渐加入，可能会使Pb-Sn合金的横声学波带变为虚的，导致铅锡合金的相变.

3.3 热力学性质

利用前面Pb-Sn合金和Pb的声子态密度，可得到在298.15 K下两者的等体热容CV，熵S，自由能F以及内能E，其对比值如表1.

表1 在298.15 K下Pb-Sn合金和Pb的等体热容CV，熵S，自由能F以及内能E

根据本人已所做结果[15]的熔化机理可知，Pb-Sn合金在x= -0.35时斜方结构和x= -0.5之间的能量差0.1217 eV可与达到熔化温度时的振动能量接近，进而可算出Pb-Sn合金在常压下的熔化温度为198 ℃，比试验值183 ℃[1]高8.2%，其结果还令人满意.

同样地，金属Pb在x= 0时面心立方结构和简单立方结构(SC)之间的能量差0.17253 eV与达到熔化熔化温度时的振动能量接近，可得Pb在常压下的熔化温度为394 ℃，比试验值327 ℃[1]高20%，其结果偏差稍大.

4 结 论

通过优化计算Pb (60﹪)-Sn(40﹪)合金和Pb两者的晶格参数、能量、电子能带以及态密度、声子能带以及态密度，然后利用两者的声子态密度，计算得到两者在标准条件下(298.5 K，1atm)热熔、熵、自由能、内能和熔化温度等热力学性质，同时对两者的所有计算结果进行了比较. 尤其是采用本人已做的结果[15]中的固-液相变机理，得到Pb-Sn合金的熔化温度与实验结果还令人满意. 但Pb的熔化温度与实验结果相比偏差稍大，可能是由于各个物质的各异性、复杂性，熔化机理还需更进一步讨论和继续完善.