基于OpenSees的形状记忆合金驱动力本构的开发

刘振勇，马嘉良，张梦梅，李培刚

（上海应用技术大学 轨道交通学院,上海 201418）

形状记忆合金（shape memory alloy,SMA）是一种土木工程智能材料，利用其独特的形状记忆效应产生驱动力[1]，可实现对土木工程结构的智能控制。袁磊[2]对NiTi合金进行循环荷载试验，得到不同通电状态和预应力状态时不同的恢复力模型，提出SMA主被动控制系统能有效的控制结构加速度和层间位移；陈斌[3]通过微观材性试验，发展塑性与相变耦合的SMA宏观本构模型，提出考虑塑性变形的SMA的自由能表达式，结合Abaqus模拟，证明本构的可靠性；李双蓓等[4]测试了SMA在不同电流方案和不同初始应变下的回复性能，通过拟温度荷载法模拟温度变化对回复力的影响；陈翔等[5]对NiTiNb合金在不同预应变和温度下的驱动力进行研究，考虑马氏体逆相变受塑性变形的影响,构建相变和塑性耦合的形状记忆合金本构模型，用Abaqus模拟SMA热机耦合作用过程，结果与试验结果吻合。在目前研究中，研究者们大多关注于SMA的应用，对SMA驱动力本构研究不够充分。

现有的SMA驱动力本构主要分为3类：①基于热力学理论的模型[6-11]；②基于黏塑性理论的模型[12-13]；③基于晶体理论的模型[14-15]。在以上3类模型中，部分模型虽公式简单，但是适用范围有限，例如Tanaka模型、Liang-Rogers模型，另一部分函数关系复杂，不适合工程应用，例如Ivshin-Pence模型、Achenbach-Muller模型。

OpenSees[16-17]是一个开源有限元程序，其材料库中具有较丰富的钢筋材料本构和混凝土材料本构，目前广泛应用于混凝土结构分析。但OpenSees材料库中目前尚没有SMA驱动力本构。本文以SMA驱动力试验为基础，建立能够综合反映预应变、温度等因素影响的驱动力本构，并将SMA添加到OpenSees材料库中，试图为基于OpenSees的SMA应用研究提供实现路径。

1 SMA驱动力本构模型

文献[18]中的SMA驱动力试验中，试样采用镍钛形状记忆合金。首先将试样拉伸至设计值，然后卸载，再将试样固定于图1所示的钢架装置，测量SMA升温和降温过程中驱动力随温度的变化关系。通过测量不同预应变的SMA驱动力，研究驱动力与预应变的关系。

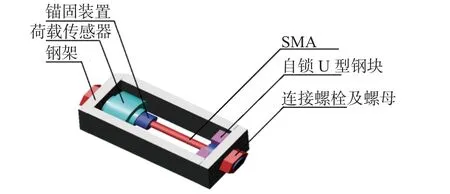
图1 实验装置Fig.1 Experimental installation

试验装置如图1所示，主要包括钢架、SMA、锚固装置、荷载传感器、自锁U形钢块、连接螺栓及螺母。其中，SMA的端部直径为10 mm，端部向内150 mm范围内直径过渡为6 mm，SMA圆柱段的直径为6 mm。

SMA驱动力试验数据详见文献[18]，以试验数据为基础，本文提出SMA驱动力本构，分为升温阶段和降温阶段。

1.1 升温阶段

驱动力与温度的关系可分为3个阶段。

第1阶段T＜Ams，马氏体逆相变前，驱动力与温度之间呈线性关系：

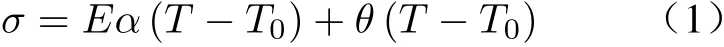
第2阶段Ams≤T≤Amf，发生马氏体逆相变，驱动力大小受到预应变ε0、初应力σ0、温度T的影响，且与温度呈正弦关系：

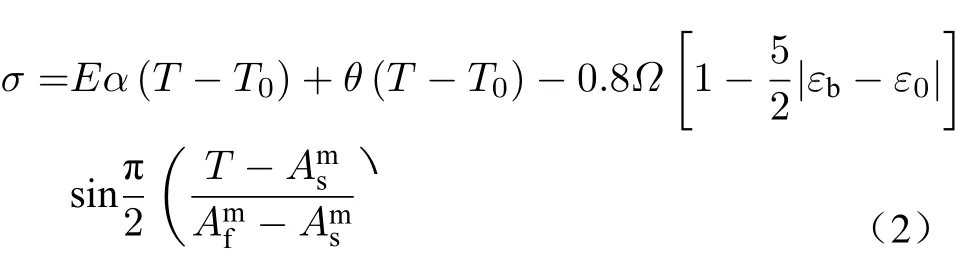
T＞Amf

第3阶段，马氏体逆相变后，驱动力与温度之间呈线性关系：

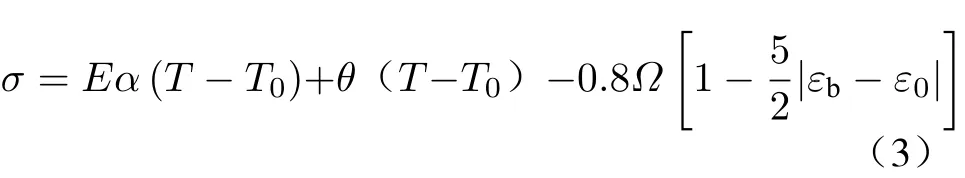
1.2 降温阶段

驱动力与温度的关系可分为3个阶段。

第一阶段：（T＞Mms），马氏体相变前，驱动力与温度呈线性关系

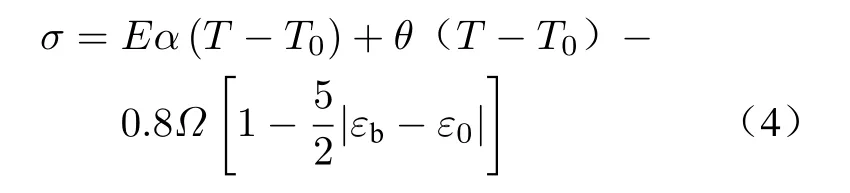
第二阶段：（Mmf≤T≤Mms），发生马氏体相变，相变力与温度之间呈正弦关系

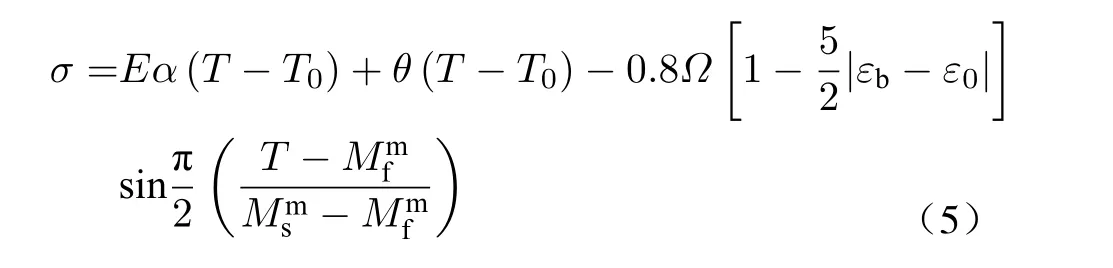
第三阶段：（T＜Mmf），马氏体相变后，驱动力与温度之间呈线性关系

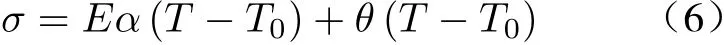
式中：E为SMA弹性模量；α为线弹性系数；Ω为相变模量；θ为热弹性模量；T0为初始温度；ε0为预应变；εb为 最佳预应变；Msm、Mfm为马氏体相变开始温度及结束温度；Ams、Amf为奥氏体相变开始温度及结束温度。

2 基于OpenSees的驱动力本构开发

Opensees是一个开源有限元平台，采用面向对象的编程范式，允许开发人员在Visual Studio平台中添加新的材料模块，主要包括配置编译环境和新建SMA子类。

在Visual Studio平台配置编译环境，集成Active Tcl解析库、Intel Parallel Studio XE并行计算库、Git控制系统，环境编译简图如图2所示。

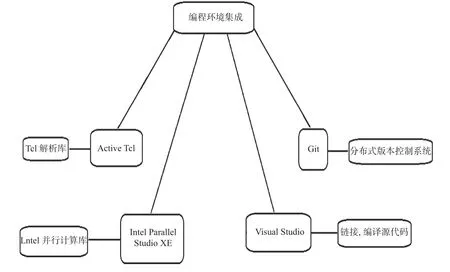
图2 环境编译Fig.2 Environmental compilation

在OpenSees材料库中新建SMA子类，主要包括2部分：①创建头文件SMA.h，包括继承成员函数和设置私有成员变量；②创建源文件SMA.cpp，包括接口函数和SMA子类成员函数。

2.1 创建头文件SMA.h

OpenSees可实现对数据的封装、类的继承及函数的重载等功能。对于二次开发而言，应根据需要建立派生类并重载基类成员函数。在OpenSees中添加SMA材料需要通过继承UniaxialMaterial类实现。头文件SMA.h定义了继承的Uniaxial-Material类的接口和变量，主要包括公有成员函数和成员变量的声明，及私有成员变量的设置。具体代码如下：

class SMA:public UniaxialMaterial {

public:

SMA(tag,heating_state,T,E,θ,A ms,A mf,

Ms m,Mf m,T0,ε0,εb,α);…

private:

bool heating_state;

doubleT;

doubleE;

doubleθ;…}

此时，tag表示材料编号，heating-state表示升温状态，其他符号定义见1.2节。

2.2 创建成员函数文件SMA.cpp

成员函数文件是对SMA.h文件中声明的公有成员函数进行补充定义，单轴材料类的公有成员函数如表1所示。

表1 单轴材料类主要成员函数Tab.1 Principal member functionsof uniaxial materials

具体步骤如下：

（1）定义构造函数UniaxialMaterial。

构造函数UniaxialMaterial定义SMA的数据变量：

SMA::SMA (tag, heating_state,T,E,θ,A ms,A mf,Ms m,Mf m,T0,ε0,εb,α):

UniaxialMaterial (tag,MAT_TAG_SMA),

heating_state(heating_state),…

（2）定义setTrialStrain函数。

在此函数中定义SMA驱动力本构关系，是材料添加的核心函数之一，SMA的驱动力本构流程图如图3所示（图编号、表编号）。

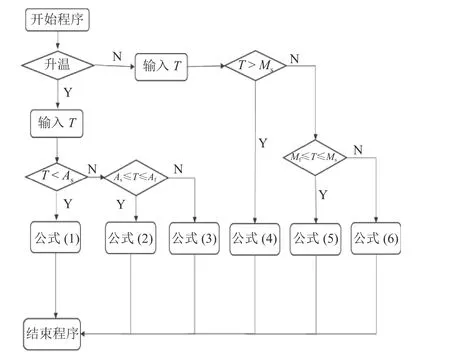
图3 SMA驱动力本构模型流程图Fig.3 Flow chart of SMA driving force constitutive model

（3）定义commitState函数。

commitState函数在一个迭代步收敛后被调用，用于替换初始状态，给下一迭代步提供初始条件，若下一迭代步不收敛，则提供回退到上一迭代步的方法。

int SMA::commitState(void){

commit_tangent=trial_tangent;…}

（4）定义revert函数。

revert函数包括revertToLastCommit和revertToStart函数，当出现不收敛状态时，调用此函数回退到上一迭代步和初始值。

revertToLastCommit函数设置如下：

int SMA::revertToLastCommit(void){

trial_tangent=commit_tangent;…}

revertToStart函数设置如下：

int SMA::revertToStart(void){

trial_tangent=0;…}

（5）定义*getCopy函数。

此函数被构造函数调用，用以产生SMA材料的唯一副本，设置如下：

UniaxialMaterial*SMA::getCopy(void){

SMA* theCopy = new SMA (this-＞getTag (),

heating_state,T,E,θ,Ams,Amf,Ms m,

M mfT0ε0εbα

, ,,,);

theCopy-＞trial_tangent = trial_tangent; …}

（6）定义send Self /recvSelf函数。

用于发送和接收SMA数据到数据库，最终形成输出结果。

send Self函数如下所示：

int SMA::send Self(int cTag,Channel&theChannel){

static Vector data (20);

data (0)=this-＞getTag();…}

recvSelf函数如下所示：

int SMA::recvSelf(int cTag,Channel&theChannel,…){

static Vector data(16);…}

3 SMA驱动力本构模型验证

基于OpenSees平台，建立文献[18]中SMA试验模型，SMA筋长度为150 mm，直径为6 mm，各参数与文献[18]保持一致。

采用dispBeamColumn单元、Fiber截面，使用Load Control加载，NormUnbalance收敛准则，KrylovNewton迭代算法进行分析，模型如图4所示。

图4 仿真分析Fig.4 Simulation analysis

SMA材料参数如表2所示。

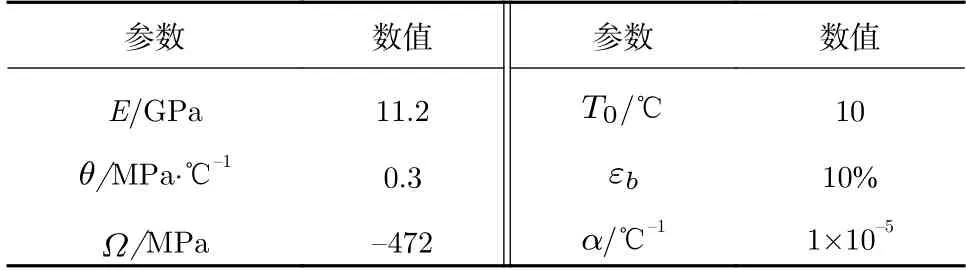
表2 SMA材料参数Tab.2 SMA Material Parameters

不同预应变下，SMA的相变温度如表3所示。

表3 不同预应变下的相变温度Tab. 3 Phase transition temperature of different prestrains

3.1 驱动力——温度关系验证

以预应变为8%的SMA为例，模拟了升温过程(10～186℃)和降温过程(32～186℃)中驱动力与温度的关系，结果如图5所示。可见：计算最大应力值为455.3 MPa，试验得最大应力值为465.2 MPa，两者之间的误差为2%，吻合良好。

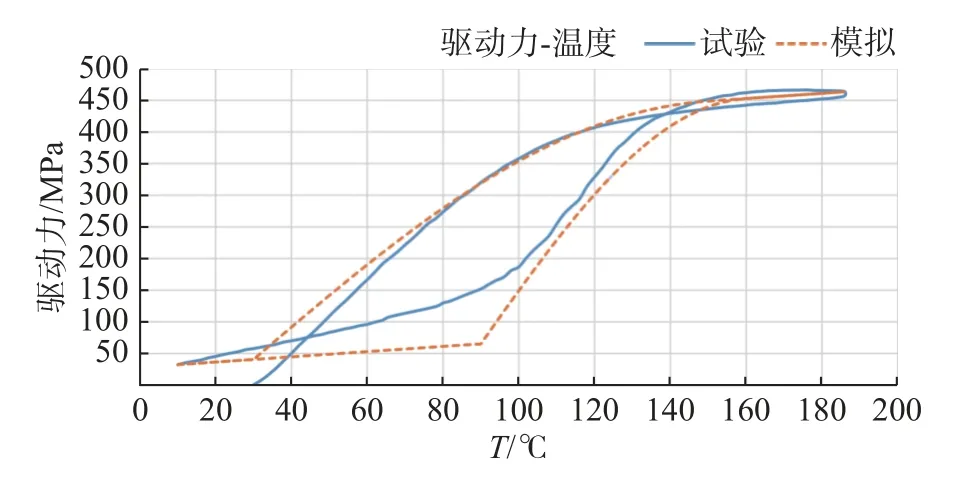
图5 8%预应变的驱动力与温度关系Fig.5 Relationship between driving force and temperature of 8% prestrain

3.2 驱动力——预应变关系验证

当SMA的预应变发生变化时，其驱动力会随之发生变化。本文分别计算了SMA预应变为4%、6%、8%、10%、12%的驱动力，计算结果与试验均吻合较好。其中在不同预应变下，升温过程中最大驱动力试验值与计算值如表4所示。

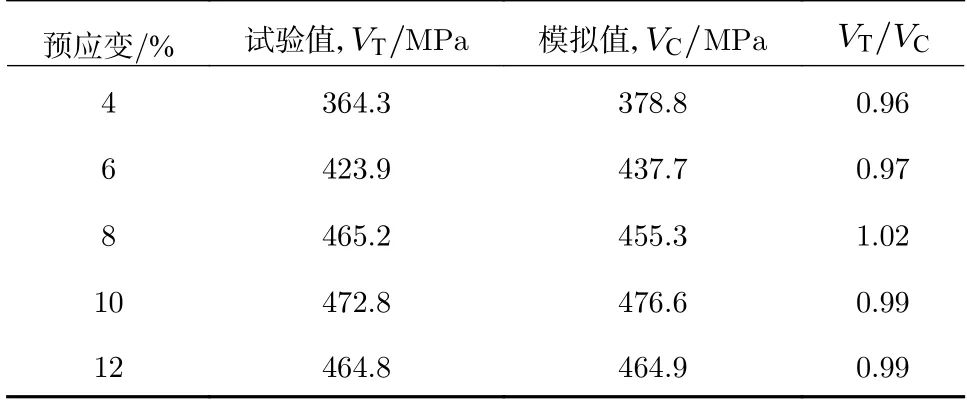
表4 试验与计算最大驱动力Tab.4 The maximum driving force of test and calculate

最大驱动力随着预应变的增大而增大，预应变为10%时最大驱动力值最大，为472.8 MPa；当预应变继续增大时，最大驱动力反而有所减小。

4 结语

根据SMA驱动力试验得到的数据，本文提出能够综合反映预应变、温度等因素影响的SMA驱动力本构。SMA的最大驱动力随着预应变的不同而变化，存在一个最佳预应变。最佳预应变对应的驱动力最大。本文所用SMA最佳预应变为10%。不同预应变的SMA在驱动过程中的驱动力变化规律相同。在相变发生时，驱动力与温度呈正弦函数变化关系。在相变前后，驱动力与温度呈线性变化关系。

通过Visual Studio平台集成Active Tcl解析库、Intel Parallel Studio XE并行计算库、Git分布式版本控制系统，配置编译环境。通过创建UniaxialMaterial类的头文件和成员函数文件，创建SMA子类，将SMA驱动力本构添加至Open Sees材料库。利用本文开发的SMA本构，基于OpenSees平台进行了模拟计算，结果与试验数据吻合良好。

需要指出的是，因试验数据样本有限，后续研究应围绕提高模型的精度及准确性展开，这就需要更多的数据样本。