具有输入饱和的机车牵引传动系统自适应跟踪控制
刘芳璇,谢程程
(西安铁路职业技术学院,陕西,西安 710028)
0 引言
在牵引工况下,机车电机产生的牵引动力通过减速齿轮传至轮对,并利用轮轨黏着产生牵引力驱动机车。机车运行时,轮对踏面承受车体静载荷和动态冲击载荷致使负载折算后牵引电机转子转轴所受外部扰动影响增强,齿轮磨耗程度增加,影响牵引传动的可靠性和电机的转速控制精度,应通过削弱外部扰动提升电机的运行品质。
常见的削弱扰动的方法是针对扰动的类型合理设计观测器,并结合控制器进一步降低观测误差对系统输出的影响,最终使得系统闭环跟踪误差有界收敛。张刚[1]和丁稳房等[2]设计了添加比例——积分(PI)锁相环的滑模观测器,旨在消除高频抖动。但该文对锁相后扰动观测结果缺乏分析,且采用PI控制无法确保跟踪观测实际扰动;牛绿原[3]和姜建国等[4]设计了基于Sigmoid函数的自适应模糊滑模观测器,并将其引入电机转速闭环用来估计转速与转子位置,但其模糊规则难以根据时变扰动随时调整,致使转速估计存在较大误差。
实际工况中,电机的工作电压受限于标准电压。同时,为了避免电子元件过压超载导致系统失控,应在控制器输出端设置饱和控制器。饱和控制器虽能限制电压幅值,而饱和非线性却会导致控制量的输出特性在饱和限幅以外的部分被截断,只有饱和限幅以内的部分则不受影响[5]。此外,随着对牵引传动系统性能要求的逐步提升,仅针对闭环输出误差设计的PI控制器已难以应对高阶耦合非线性。
根据上述分析,本文针对机车牵引传动系统设计控制器,通过引入饱和辅助控制系统、构造转速误差面和虚拟控制律并采用微分跟踪器和反推法设计电压控制器;构建非线性扰动观测器分别估计转子轴和负载轴的时变扰动,对估计误差采用自适应模糊逼近,并将此逼近值引入控制器以补偿扰动估计误差。本文所设计的控制器可使受控系统快速跟踪参考输入并精确估计外部扰动的实时变化,兼顾动态响应快速性和时变扰动鲁棒性。
1 自适应跟踪控制器设计
1.1 机车牵引传动系统模型
为推导牵引传动系统的数学模型,特对牵引电机做如下假设[6]。
(1) 不计铜耗和铁耗。
(2) 忽略铁芯饱和效应。
(3) 不考虑齿隙传动伺服补偿。
图1为牵引传动系统示意图。
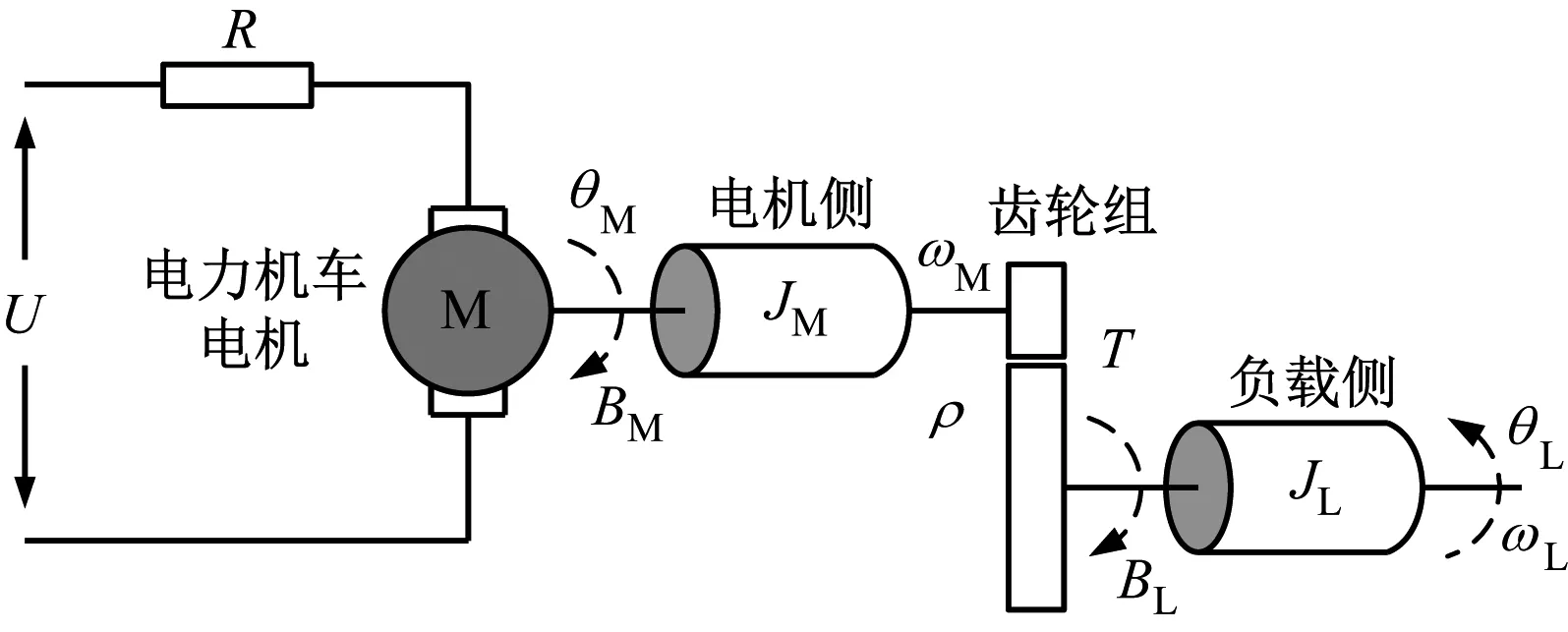
图1 机车牵引传动系统
系统的数学模型为
(1)
式中,θL、θM、WL、WM分别为负载轴和电机轴的转动角度和转速,JL、BL、JM、BM分别为负载轴和电机轴的转动惯量和粘滞摩擦阻尼,Kθ和KT分别为电机转矩系数与电机常数,U为控制电压,R为等效电阻,ρ为齿数比,dL、dM分别为负载轴和电机轴的外部扰动。
选取状态变量如下:x1=θL,x2=ωL,x3=θM,x4=ωM,将式(1)化为状态方程,得:
(2)
本文的控制目标是为系统设计自适应跟踪控制器,在系统控制量存在饱和及外部存在干扰的情况下,能够确保系统输出尽快跟踪期望的参考轨迹,且系统闭环信号有界。
1.2 具有输入饱和的自适应控制器设计
饱和限幅前后系统控制量存在关系如下[9]:
(3)
式中,V、U分别为饱和限幅前后控制量,uM为饱和限幅。
设计饱和辅助控制系统为
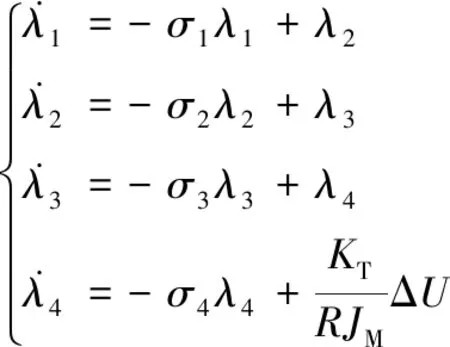
(4)
式中,ΔU=sat(V)-V为饱和限幅差,λ1、λ2、λ3、λ4为辅助变量,σ1、σ2、σ3、σ4为非负增益。
对λ1分别求算其二至四阶导数,有:
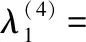
定义:
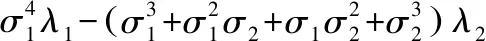
-(σ1+σ2+σ3+σ4)λ4
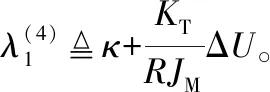
假设参考轨迹xd及其各阶导数存在。定义x1的跟踪误差e1为
e1=x1-xd-λ1
(5)
式中,xd为期望轨迹。
(6)
式中,k1>0为待定增益。
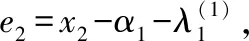
(7)
式中,ζL和χL为辅助变量,L1>0为辅助增益。
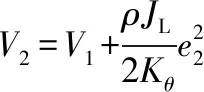
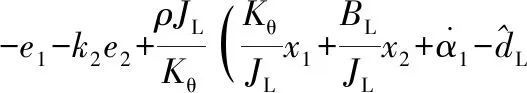
(8)
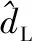
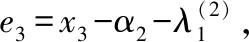
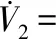
(9)
式中,k3>0为待定增益。
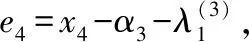
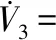
(10)
式中,ζM和χM为辅助变量,L2>0为辅助增益。
设计NDO输出至控制器部分的控制量为
(11)
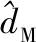
同时注意控制器内部关系:
U=V+ΔU=Vat-Vf+ΔU
(12)
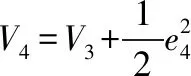
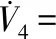
(13)
设计Δ1的估计律为
设计自适应模糊控制器为
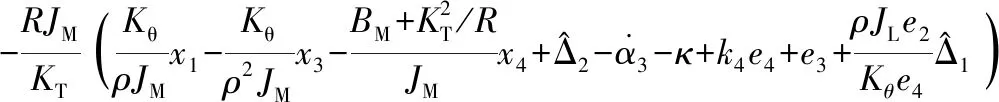
(14)
式中,k4>0为待定增益。
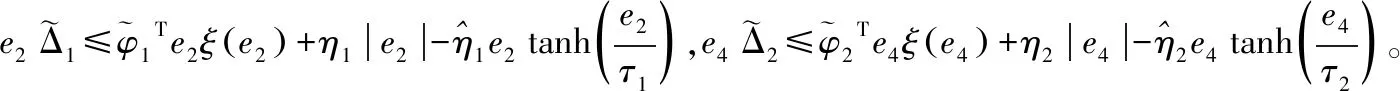
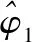
(15)
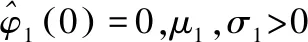
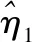
(16)
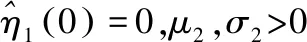
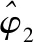
(17)
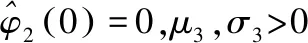
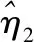
(18)
1.3 闭环稳定性证明
引理1 (Young’s不等式[11])
(19)
式中,p>1,q>1,并且(p-1)(q-1)=1。
引理2 (微分跟踪器[12])
(20)
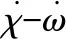
引理3[13]对任意σ>0和ϑ∈R,下述不等式成立:
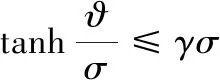
(21)
式中,γ为常数且满足γ=e-(γ+1),i.e.,γ=0.278 5。
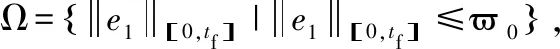
证 定义Lyapunov泛函为
(22)
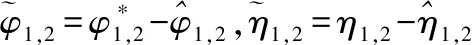
对式(22)求导,并进行化简可得:
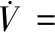
(23)
根据引理1得:
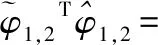
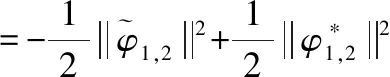
(24)
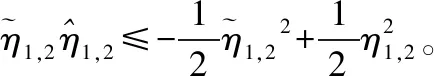
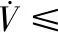
(25)
其中,
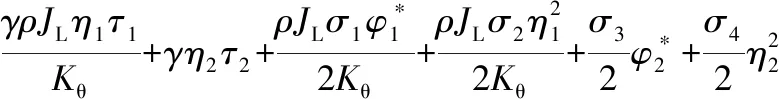
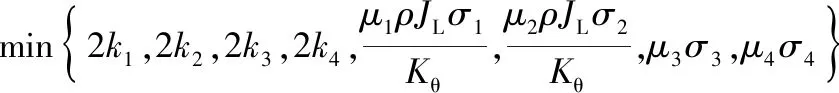
2 仿真结果及分析
在SIMULINK仿真环境(MATLAB_R2018a)中对机车牵引传动系统采用具有输入饱和的自适应跟踪控制器进行仿真研究。仿真框图见图2。
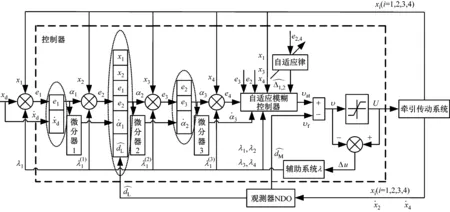
图2 具有输入饱和的牵引传动系统仿真模块框图
设定输入指令为xd=1-cos(5·t)。负载轴和转子轴分别承受冲击载荷为
(26)
机车牵引传动系统参数见表1。
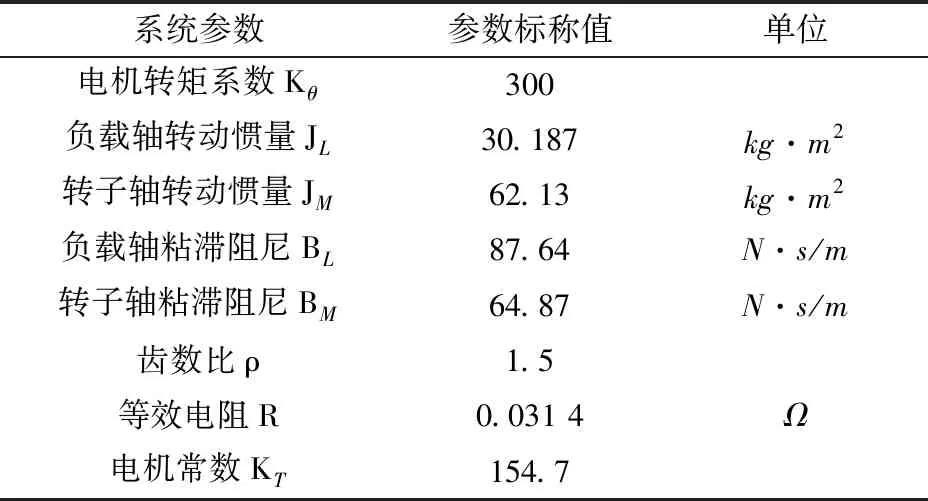
表1 机车牵引传动系统参数标称值
图3为系统输出x1对输入指令xd的跟踪误差及其对数数量级曲线。分析可知,x1能够在0.1 s内(图3子图1)迅速且精确跟踪xd,其跟踪误差均在e-20~e-5范围内变化,即跟踪误差对数数量级变化范围集中在-20至-5,对数数量级越小说明x1对xd的跟踪性能越强。图3子图2呈现的是2至5 s内的跟踪情况,显然,从2.5 s和3.8 s开始,跟踪效果有所降低,其原因为系统控制量受饱和限幅影响,由于限幅以外控制量的输出特性被截断,导致系统输出无法有效跟踪输入指令。同样地,在图3子图3中,虽然跟踪误差在±0.01内变化,但在第5.8 s和第7 s这两个时刻处的跟踪误差明显较大。考察图6可知,系统控制量在对应时刻均存在饱和现象。
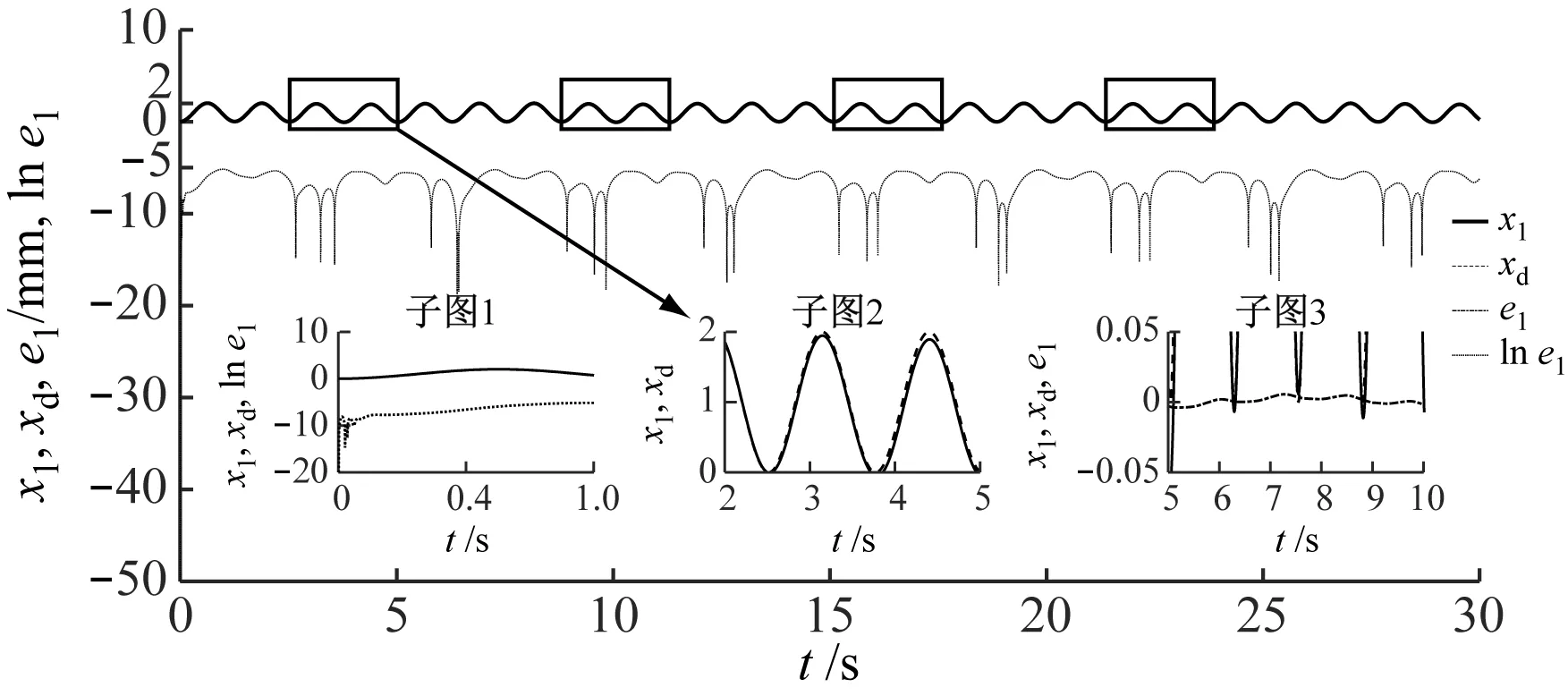
图3 输入指令跟踪曲线
图4分别为负载轴和转子轴的扰动估计误差及其对数数量级曲线。由两幅子图可知,负载轴和转子轴的扰动估计值均能够在0.01 s内实现对实际值的跟踪,其跟踪误差分别收敛于±0.3和±0.6。参照对数数量级曲线可知,误差分别稳定在e-15~e0(dL)和e-12~e0(dM)范围内。这表明,本文所设计的NDO可有效且精确估计外部扰动。
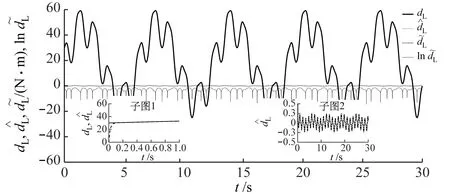
和
图5为微分跟踪器对虚拟律的跟踪误差及虚拟律的微分曲线。由于直接求取虚拟控制律微分的解析表达式会引入大量计算,增加控制器的构建难度,故采用微分跟踪器对虚拟律进行整体微分。对比分析图5(a)和图5(b)的子图1,易知在0.1 s短暂的振荡后,微分跟踪器的输出能够实现对虚拟律的跟踪,其跟踪误差分别在±0.15和±10范围内规律变化(图5子图2)。考虑纵坐标数量级,认为微分跟踪器能够精确跟踪虚拟律,由引理2可知跟踪器输出的虚拟律的微分能够有效逼近虚拟律微分的解析解。对比分析两幅图的子图3和子图4,可知虚拟律的微分在2.5 s和3.8 s及5.8 s和7 s附近存在小幅波动现象,其产生时间与图6中时刻相同,说明饱和限幅亦会影响虚拟律的微分。
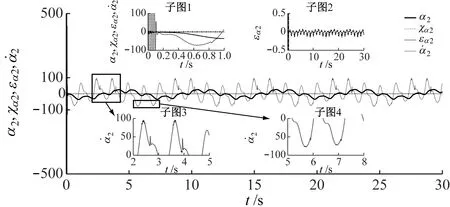
(a) α2、χα2、εα2和
图6为系统饱和限幅前、后控制量曲线。仿真中设定饱和限幅为±220。分析图6及其子图可知,由于饱和限幅对控制量超出幅值的有用信息进行了强制切除,导致图3及图5中跟踪及微分曲线突变;而控制量在饱和限幅内,则不会被截断,其曲线光滑平整,对应输出和虚拟律跟踪误差(图5子图2)及微分曲线抖振较小。
综上可知,对于采用自适应跟踪控制的牵引传动系统,其闭环输出快速稳定跟踪输入指令;NDO精确跟随外部扰动;微分跟踪器精确跟踪虚拟律变化并有效输出虚拟律的微分;在饱和限幅内,系统控制量光滑无抖振。
3 总结
本文针对具有输入饱和的机车牵引传动系统,设计了基于NDO和微分跟踪器的自适应反推控制器。针对控制量输入饱和,设计了饱和辅助控制系统;针对系统负载轴和转子轴所受的时变扰动,设计了NDO对其分别跟踪观测,观测误差进行自适应模糊估计,并由此推导出观测误差的自适应律。由仿真结果知,本文设计的控制器具备优势如下:
(1) 采用微分跟踪器输出虚拟律的微分解决传统反推控制中对虚拟律求导产生的计算膨胀问题;
(2) 饱和辅助控制器中引入控制量限幅差补偿跟踪性能受饱和限幅的影响,实现限幅内快速收敛;
(3) 采用自适应模糊估计观测误差,降低扰动对系统跟踪性能的影响。

