开口尺寸和铺层比例对复材层合板压缩性能的影响

杨钧超, 邓凡臣, 柴亚南

（1．中国飞机强度研究所 复合材料结构强度研究室, 西安 710065；2．全尺寸飞机结构静力/疲劳航空科技重点实验室, 西安710065）

复合材料具有比强度和比刚度高、可设计性强、疲劳性能好、质量轻、耐腐蚀等优异性能，被广泛应用于航空航天领域[1-3]。先进飞机的机翼、机身、水平安定面、垂直安定面等部位大量使用了复合材料层合板结构。为了保证机械连接、油路管道通过、设备安装、检查维修等，在层合板上布置大小不同的开口不可避免。开口会导致结构传力路径中断、刚度突变、应力集中等问题，严重降低结构的承载能力。因此，评价和预测复合材料层合板开口结构的强度和失效模式一直是结构设计人员研究的方向。

目前，国内外学者采用了多种方法对复合材料层板开口性能进行研究。在工程预测方法方面，吴义涛等[4]基于应力场强法的思想，提出了一个预测含圆孔复合材料层合板剩余强度的工程简化模型，该方法预测精度比点应力准则和平均应力准则更优。在数值分析方法方面，Chang等[5-6]提出二维渐进损伤分析有限元模型，考虑了剪切非线性和横向拉伸强度和剪切原位强度，分析含孔复合材料层合板的孔边应力集中，并预测了拉伸、压缩强度；Hallett等[7]在可能分层的分离面处植入界面单元，用来模拟层间分层失效，并对四种不同铺层的含双边缺口和含中心圆孔层合板的拉伸失效行为进行深入研究，得到的失效模式和剩余强度与实验结果一致。Pham等[8]采用三维连续壳单元模拟含双边缺口复合材料层合板，层间界面采用三维黏聚力单元模拟，选用几种不同的单层失效准则进行对比分析。李彪等[9-10]将LaRC05准则[11]发展为适用于平面应力问题的失效准则，提出了对应的连续型损伤演化方法，有效预测了复合材料层板开口拉伸强度。许良等[12]利用有限元软件 ABAQUS 建立三维逐渐损伤失效模型，研究不同开口形状对国产T700/双马树脂基复合材料层合板拉伸性能的影响，结果发现含圆孔的层合板拉伸强度最大，然后依次是椭圆孔、方形孔、菱形孔。鲍宏琛等[13]建立三维有限元模型研究准各向同性纤维增强复合材料层合板单向拉伸时的缺口尺寸效应和缺口形状效应，模拟得到的层合板破坏强度与实验结果对比取得很好的一致性。李亮等[14]研究了矩形开口长度和角度对层合板剩余强度的影响规律，建立了剩余强度与切口损伤尺寸的定量关系。王刚等[15]研究了圆形切口和长条形切口对复合材料层合板力学性能的影响，发现两种中心切口形式的复合材料层合板损伤进程有较大差异，但两者的拉伸强度较为接近。张谦[16]通过数值模拟，分析了不同铺层角对含孔复合材料层合板孔边应力和应变分布的影响，并指出正交0°/90°铺层能有效缓解孔边应力集中，提高含孔复合材料的力学性能。

以上研究多针对开口尺寸较小的情况，对开口尺寸较大的情况研究较少。Li等[17]和黄河源等[18]研究了含大开口复合材料层板剪切强度问题，陈建霖等[19]和王力立等[20]研究了含大开口结构在拉伸载荷下的失效行为。然而，现有大开口结构的研究多基于数值计算分析，针对实验测试结果进行损伤破坏模式、机制的研究较为欠缺，特别是压缩载荷下的强度分析。从“破坏分析奥运会”的结果来看，仅仅是单向带，各强度准则也无法完美地预测所有实验结果，因此大开口层合板压缩强度实验研究十分必要。

本研究针对M21C/IMA复合材料大开口层合板，采用实验和数值模拟的方法，研究压缩载荷下的破坏机制，并分析铺层以及开口尺寸对开口区应变集中、强度和破坏模式的影响，为提高大开口复合材料结构的安全性和可靠性提供参考。

1 实验材料与方法

1.1 实验材料

试件采用的材料为中模高强碳纤维增环氧强树脂基复合材料单向带（M21C/IMA）。试件在热压罐中成型，固化温度、压力为：(177±6) ℃、0.62 MPa，固化后单层名义厚度为0.191 mm，均采用手工铺贴工艺制造。M21C/IMA材料性能见表1，其中：E1、E2、G12分别表示单向带纵向弹性模量，横向弹性模量及剪切模量，EF为 纤维弹性模量；ν12、 ν12F分别为单向带和纤维的泊松比；XT、XC、YT、YC、SL分别为单向带纵向拉伸/压缩强度、横向拉伸/压缩强度及面内剪切强度；β为剪切非线性系数；G2C为横向拉伸临界能量释放率，G12C为剪切临界能量释放率。临界能量释放率参考文献[21]取值，其余性能参数由实验测得。

表1 M21C/IMA性能参数Table 1 Properties parameters of M21C/IMA

1.2 试件尺寸及数量

大开口复合材料层板试件尺寸示意图及贴片位置如图1所示，L、W、D分别表示实验件长度、宽度和开口直径；L1为端部夹持长度。在实验件正反两面，背对背贴片（括号内为背面应变片编号）。在距孔边d=10 mm处，对称地粘贴了4个花片（编号分别为：101～103、201～203、106～108、206～208），花片小号沿着0°方向，大号沿着90°方向，中间编号的片沿着±45°方向。在距孔边d=2 mm处，对称地粘贴了4个单片（编号分别为：104、204、105、205）。

图1 大开口复合材料层合板尺寸及应变片位置示意图Fig. 1 Dimensions of large-opening composite laminates and locations of strain gauges

试件尺寸如表2所示，共有3种铺层，每种铺层包含3种结构尺寸，共9组，每组3件，合计27件。表2中，A、B、C为铺层编号，编号为A的铺层顺序为[45/−45/0/0/90/0/45/−45/0/45/−45/0/90/45/−45/0/0/45/−45/0]S，编 号 为B的 铺 层 顺 序 为[45/−45/0/90/0/45/−45/0/45/−45/90/45/−45/0/0/45/−4 5/0/−45/45]S，编 号 为C的 铺 层 顺 序 为[45/0/−45/90]5S，各铺层名义厚度h均为7.64 mm。A、B、C三种铺层的0°层、±45°层、90°层的比例分别为：40∶50∶10、30∶60∶10、25∶0∶25。

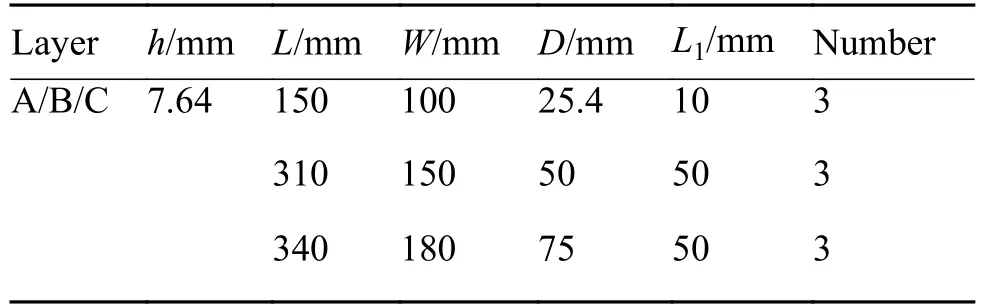
表2 大开口复合材料层合板试件尺寸及数量Table 2 Size and number of experimental pieces of large-open composite laminates

1.3 实验方案

实验均在MTS1000kN试验机上进行，加载方式均为位控连续加载，加载速率为1 mm/min。实验中采用ST16数据采集仪对试件的应变，试验机端部载荷进行同步实时测量。

2 数值模型

采用商业有限元软件ABAQUS，编写了用户自定义场子程序（USDFLD），建立复合材料的失效模型。分别用场变量FV1、FV2、FV3表征纤维失效(fiber failure，FF)，纤维间失效(inter-fiber failure，IFF)和剪切非线性效应，并对相应的材料属性进行退化；用状态变量SDV1、SDV2来区分纤维拉伸压缩失效，用状态变量SDV3、SDV4来区分纤维间拉伸/压缩失效。

2.1 复合材料失效准则及损伤演化

2.1.1 纤维失效及损伤演化

纤维失效主要是由纤维方向上的应力σ11引起。Puck等[22]认为：由于横向应力σ22的泊松效应，在纤维方向产生一个附加的微应变，树脂中的应力非均匀分布且在薄层级别上局部明显大于横向应力，泊松效应被局部放大，放大效应通过放大因子mσ,f来考虑，对于碳纤维复材取mσ,f=1.1。纤维失效准则如下所示：

其中，

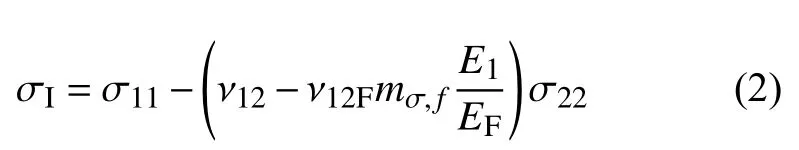
式中：σI是中间变量；fFF是纤维失效应力危险系数。当fFF≥1时，表示纤维失效。纤维失效后，纤维损伤状态变量SDV1、SDV2以及场变量FV1通过以下控制方程确定：

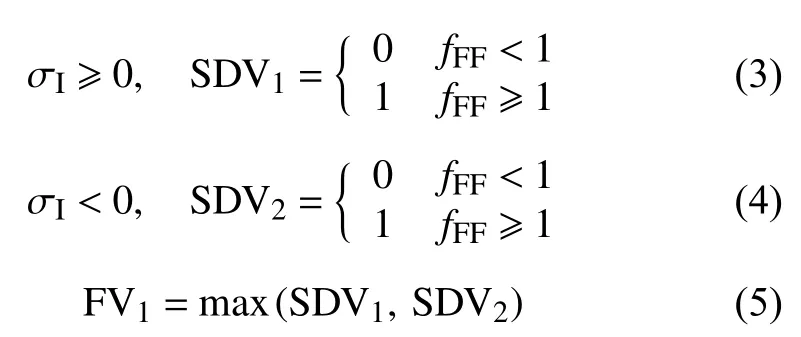
由于纤维为脆性断裂，失效后直接将损伤区内的弹 性常 数（E1、E2、ν12、G12）折减 为初 始值 的0.01%。

2.1.2 纤维间失效及损伤演化

Puck在实验中发现，纤维间失效时会产生一个平行于纤维方向的断裂面，断裂面与厚度方向的夹角θ 称为断裂角，随着应力状态的不同发生变化。

如图2所示，在横向应力σ22和面内剪切应力τ12的作用下，断裂面上应力分量包括：法向正应力σN、平行纤维方向的剪切应力τNL和垂直纤维方向的剪切应力τNT。

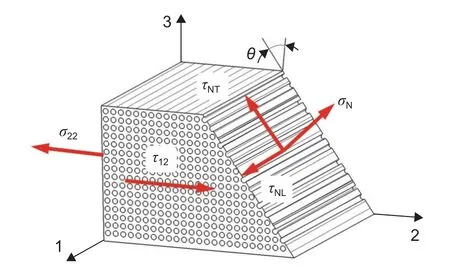
图2 横向应力和剪应力组合作用下基体断裂面示意图Fig. 2 Fracture plane under combined transverse and shear stress

断裂面上应力分量计算公式如下：

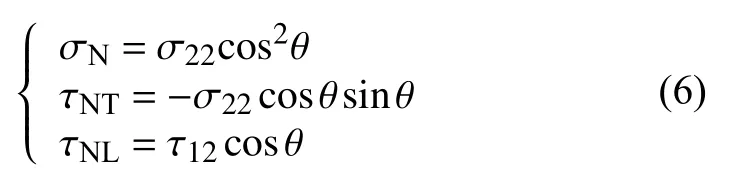
Pinho等[11]在将Puck提出的断裂面压缩/拉伸失效理论统一为如下形式：

其中，

式中：µT、 µL分 别表示横向和纵向摩擦系数；θ0为纯横向压缩时断裂面的夹角，本文参考文献[23]取53°；〈〉为 Macaulay bracket算子，对于任意x∈R，恒有〈x〉=(|x|+x)/2；fIFF是纤维间失效应力危险系数，本研究采用黄金搜索法[24]求得当前应力状态下fIFF的 最大值，当fIFF≥1时，表示纤维间失效。

对于纤维间失效，采用线性软化模型[21]描述失效后的材料性能，将E2、ν12、G12折减为初始值的(1−FV2)倍。纤维间损伤状态变量SDV3、SDV4以及场变量FV2通过如下控制方程确定：

式中：dIFF表 示纤维间损伤折减系数； εmax表示从0至t时刻加载历程最大等效应变，表征了损伤的不可逆性；ε0和εf分别表示初始失效和最终破坏时的等效应变。εN、γNL、 γNT为断裂面上正应变、平行于纤维方向的剪应变和垂直于纤维方向的剪应变，计算公式如下：

式 中：ε22、 ε33为 2、3方 向 的 正应 变；γ12为 面 内12方向剪应变。ε0等价于fIFF=1时所对应的等效应变，计算公式如下：

材料完全失效由断裂面上的临界能量释放率控制，当单元特征长度LC内应变能释放率等于临界能量释放率时完全失效，此时εf表达式如下：

其中，

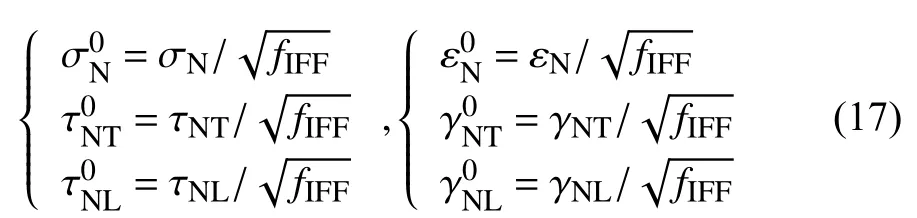
式中：σ0N、τ0NL、 τ0NT和 ε0N、γ0NL、 γN0T表 示fIFF=1时，断裂面上的应力和应变。G2C为横向拉伸临界能量释放率，G12C为剪切临界能量释放率。

2.2 剪切非线性效应

单向带的剪切非线性行为采用Hahn-Tsai[25]模型，剪切应变γ12的表达式如下：

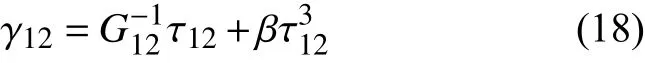
式中：β为剪切非线性系数，由实验确定。通过场变量FV3将材料的剪切刚度折减为初始值的（1−FV3）倍，据此场变量FV3通过下式确定：

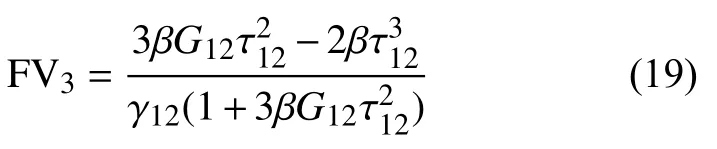
2.3 有限元模型网格及边界条件

有限元模型网格如图3所示，单元类型为：SC8R，在开口周围进行网格细化，孔边共划分了160个单元。边界条件设置如下：约束模型上下两侧边节点面外自由度及绕Y轴转动自由度；模型左边节点与点RP1耦合在一起，并约束RP1点所有平动和转动自由度；模型右边节点与RP2点耦合在一起，并约束除X方向平动自由度外的所有平动和转动自由度；加载时，在RP2点施加沿负X方向的位移。

图3 大开口复合材料层合板数值模型Fig. 3 Numerical model of composite laminates with large openings

3 结果与分析

3.1 压缩强度分析

大开口复合材料层合板强度为加载过程中试件远场名义应力σ的最大值σF，远场名义应力根据压缩载荷P计算得到，计算公式如下：

实验测得的强度值，离散系数（coefficient of variation，CV），有限元分析得到的强度值及误差如表3所示。通过对比发现：同一铺层，开口尺寸越大，压缩强度越低；同一开口尺寸时，A类铺层的强度值最大，B类铺层的次之，C类铺层的强度值最低，表现出压缩强度随0°层比例的减少而降低。数值预测强度与实验结果反映的趋势一致，对于典型铺层，大开口复合材料层合板的压缩强度主要由0°层比例控制。开口尺寸较大时数值预测的强度值与实验结果比较接近，误差大多在5%以内，最大不超过10%。开口尺寸为25.4 mm时，误差均超过10%，但不超过15%。

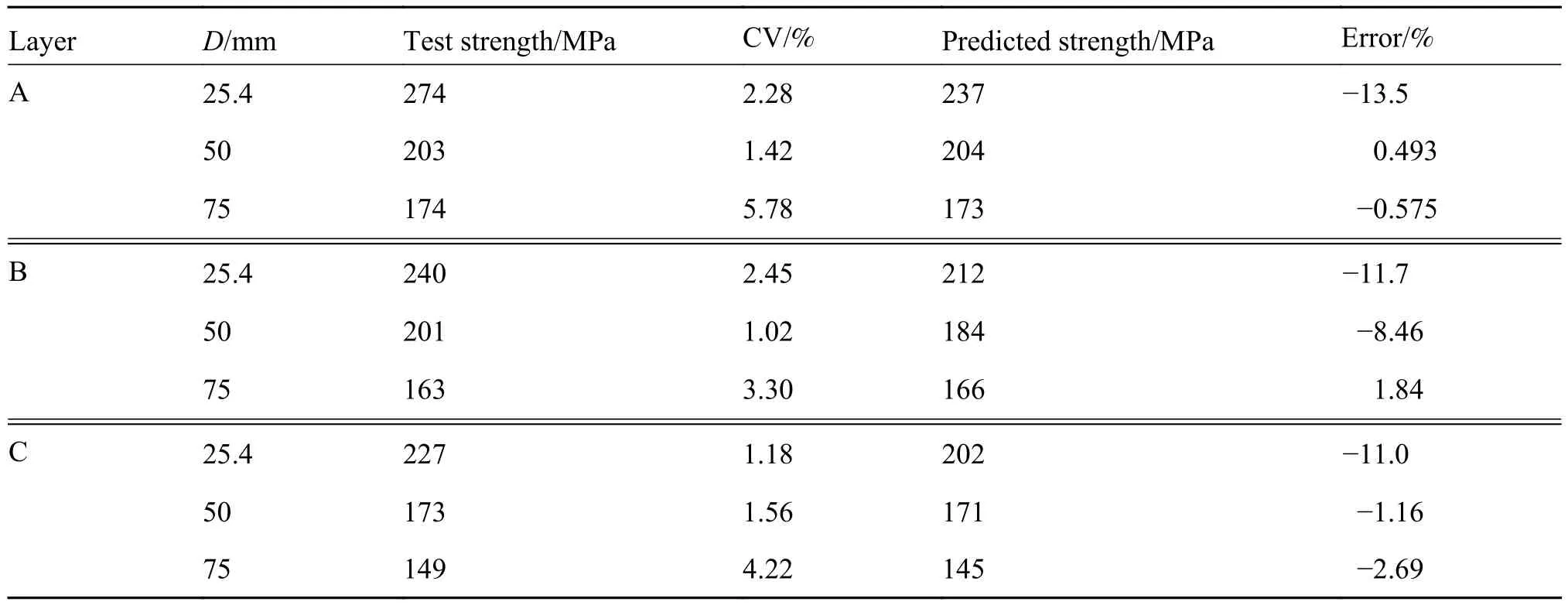
表3 大开口层合板压缩强度预测值与实验结果对比Table 3 Comparison of predicted compression strength of large open laminates with experimental results

3.2 应变分析

实验应变数据处理如下：孔边距d=2 mm处沿X方向平均正应变记为ε1，d=10 mm处沿X方向平均正应变记为ε2，计算公式如下：

式中：，εi、εj为第i、j号应变片的读数。

提取应变片黏贴位置单元应变平均值结合实验数据绘制出如图4所示的孔边平均应变-远场应力曲线。总的来看，不同铺层的大开口层板应变分布趋势一致：与孔边距离越小应变水平越高。数值分析得到的应变场分布与实验结果一致，且破坏前开口为50 mm、70 mm时应变误差很小，预测的强度也更接近实验值。数值与实验结果均反映出：铺层相同时，同一应力水平下，开口尺寸越大，与孔边距离相同区域的应变水平越高，且在试件破坏前能达到的最高应变水平偏低，从而强度值低。

图5为远场名义应力 σ=−100 MPa时，层合板孔边X方向正应变随孔边距d的变化曲线。从图5可以看出，数值预测得到的孔边应变分布与实验测试结果一致：随着孔边距离d的增大，应变水平先迅速衰减，然后缓慢降低。从图5（a）看出：铺层、孔边距离相同时，开口尺寸越大，应变水平越高，且应变随孔边距衰减得越慢，从而导致了开口尺寸大的层合板强度值低；从图5（b）看出：开口尺寸、孔边距离相同时，0°层比例越低，应变水平越高，且应变随孔边距衰减得越慢，从而导致了0°层比例低的层合板强度值低。

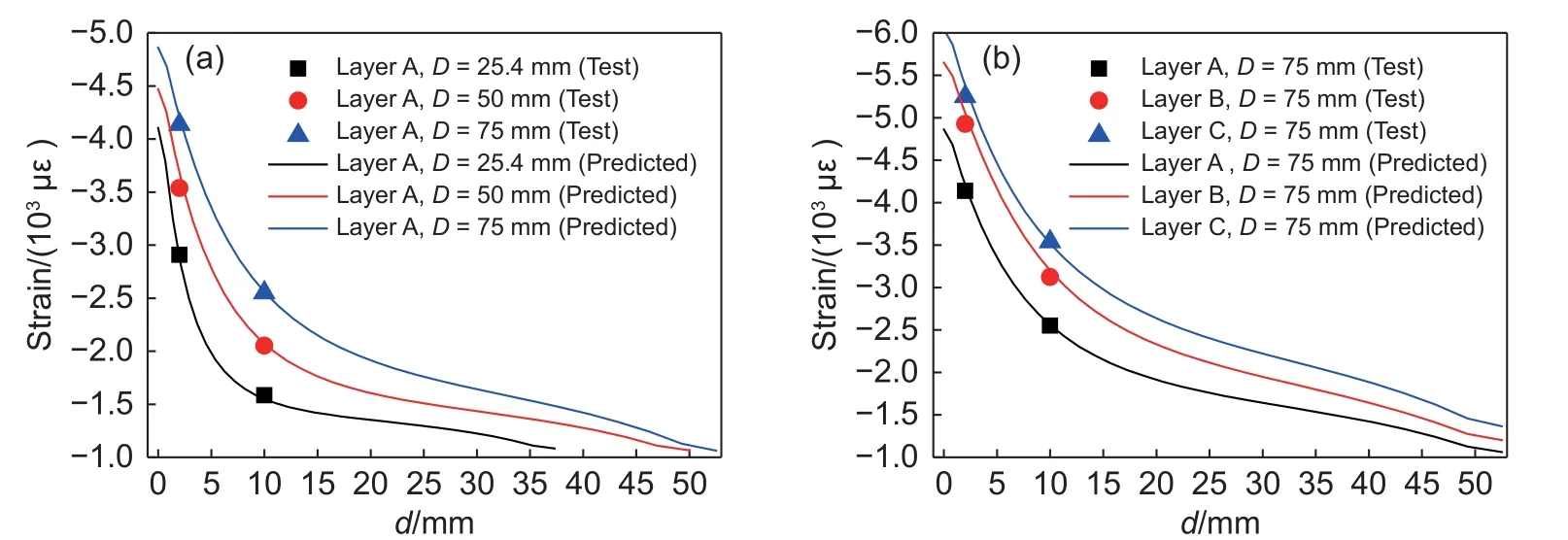
图5 层合板孔边应变随孔边距d的变化曲线（σ =−100 MPa） （a）铺层A，开口尺寸不同；（b）铺层不同，D=75 mmFig. 5 Variation curve of hole edge strain of laminated plate with hole margin d （ σ =−100 MPa） （a）layer A with different opening sizes；（b）different layer，D=75 mm

3.3 损伤分析

图6为各组大开口复合材料层合板试件破坏形貌。从图6可以看出，同一开口尺寸，不同铺层的层合板破坏模式基本相同；开口尺寸D=25.4 mm时，表面多层皱起，孔边显示出严重的分层现象，表明孔边先分层，随后被压溃。开口尺寸D=50 mm、75 mm时，主要破坏模式为纤维和基体直接被压溃。结合图4应变曲线来看，层合板失效过程如下：孔边由于应变集中首先发生局部损伤，短时间内损伤沿着横向迅速扩展至整个截面，随后完全破坏。

图4 不同开口尺寸、铺层的的层合板孔边应变-应力曲线 （a）铺层A，d=2 mm；（b）铺层A，d=10 mm；（c）铺层B，d=2 mm；（d）铺层B，d=10 mm；（e）铺层C，d=2 mm；（f）铺层C，d=10 mmFig. 4 Strain-stress curves at the orifice edges of laminated plates with different opening sizes and layer （a） layer A，d=2 mm；（b） layer A，d=10 mm；（c） layer B，d=2 mm；（d） layer B，d=10 mm；（e） layer C，d=2 mm；（f） layer C，d=10 mm

图6 不同开口尺寸和铺层的复合材料层合板破坏形貌 （a）铺层A，D=25.4 mm；（b）铺层A，D=50 mm；（c）铺层A，D=75 mm；（d）铺层B，D=25.4 mm；（e）铺层B，D=50 mm；（f）铺层B，D=75 mm；（g）铺层C，D=25.4 mm；（h）铺层C，D=50 mm；（i）铺层C，D=75 mm；Fig. 6 Failure morphology of composite laminates with different opening sizes and lamination （a） layer A，D=25.4 mm；（b） layer A，D=50 mm；（c） layer A，D=75 mm；（d） layer B，D=25.4 mm；（e） layer B，D=50 mm；（f） layer B，D=75 mm；（g） layer C，D=25.4 mm；（h） layer C，D=50 mm；（i） layer C，D=75 mm；

不同铺层下，数值模拟得到的大开口层合板破坏过程相似，因此仅对开口尺寸为25.4 mm、75 mm的A类铺层层合板进行损伤分析。图7为大开口复合材料层合板最终破坏时各单层损伤状态。从图7可以看出，D=25.4 mm和D=75 mm的大开口层合板破坏模式相同：损伤从孔边萌生，并沿着90°方向扩展进而贯穿整个截面，直至完全失效，与实验现象基本吻合。然而，实验得到的D=25.4 mm时的破坏模式还包括表面皱起分层，本工作建立的二维数值模型无法模拟层间分层的损伤模式，因而对于该开口尺寸的层合板预测精度偏低，相对误差高于10%，但不超过15%。

图7 大开口复合材料层合板各单层损伤状态（铺层A） （a）D=25.4 mm，纤维损伤；（b）D=25.4 mm，纤维间损伤；（c）D=75 mm，纤维损伤；（d）D=75 mm，纤维间损伤Fig. 7 Damage status of each single layer of composite laminates with large openings （layer A） （a） D=25.4 mm，FF；（b） D=25.4 mm，IFF；（c） D=75 mm，FF；（d） D=75 mm，IFF

4 结论

（1）开口尺寸越大，0°层比例越低，孔边应变水平越高，而应变分布梯度更小，从而大开口复合材料层合板的压缩强度越低。

（2）数值模拟得到的孔边应变分布以及压缩强度与实验结果吻合良好，开口为50 mm、75 mm时误差不超过10%；开口为25.4 mm时误差不超过15%。本研究建立的数值分析模型能够比较有效地预测含大开口的复合材料层合板的压缩性能。

（3）对于开口尺寸较小的层合板，孔边分层的影响不可忽视，建立三维数值模型分析孔边分层行为有待进一步研究。