基于子窗口盒式滤波的MPPC 微光成像增强算法

汤祥裕，尹丽菊，周 辉，邹国锋，崔玉敏，邓玉林，张言华

（山东理工大学 电气与电子工程学院，山东 淄博 255049）

引言

微光图像是在低照度环境下获得的图像，受光照强度限制及周围噪声影响，微光成像质量远低于正常可见光图像，因此图像细节增强和噪声抑制显得尤为重要。微光图像增强算法的研究有效支持了现代夜视技术的发展，如军事应用、交通信号传输、安防监控等领域，体现其巨大的潜力和广泛的应用价值。

传统的图像增强算法按照实现方式不同可分为空域和频域增强算法[1]，其中，空域增强算法包括直方图均衡化等方法，频域增强算法包括双边滤波的图像增强算法等[2]。基于频域图像增强是当前图像处理领域的热点，它要求将平滑后的图像最大限度保持图像边缘结构信息。为提高对比度的同时兼顾图像边缘信息，Liu 等在2014 年提出了一种基于引导滤波的红外图像DDE 算法 （detail enhancement for high-dynamic-range infrared images based on guide image filter, GF&DDE）[3]。算法将原图像通过引导滤波处理后得到背景层图像和细节层图像，由于引导滤波是局部线性模型，在保留图像细节的同时也减少了光晕的产生。但由于算法中采用固定合成系数的方式，场景自适应性较差，图像的基础层与细节层融合比例为定值；Zhou 等在2018 年提出了一种基于引导滤波的DDE 改进算法[4], 通过直方图分布信息为基础层图像确定门限，去除图像中无效灰度值，有效提升基础层图像对比度，但基础层与细节层的合成系数仍为定值，算法处理不同照度场景下的图像仍包含大量噪声。

红外图像在成像特点上具有图像对比度低、边缘细节模糊、随机噪声严重等问题，这与光子计数微光图像存在的特征信息具有相似性；为更好提升多像素光子计数器（multi-pixel photon counter，MPPC）探测下的微光图像可视效果，对上述红外图像分割模型改进并用其进行微光图像处理。针对上述模型中引导滤波算法平滑低照度图像不理想的情况，采用盒式滤波器与子窗口回归相结合的方式平滑初始图像，减少计算量的同时极大程度抑制了滤波输出图像的光晕现象，利用棋盘式图像验证了子窗口盒式滤波器处理低照度图像时在保持边缘和边角性能上优于引导滤波器。通过滤波后的基础层图像有效灰度值个数与整个灰度级的比例自适应确定融合比例系数，在光学实验平台上进行不同照度微光环境的仿真实验，验证本文算法能够满足自适应微光场景的图像增强。

1 算法简介

1.1 子窗口盒式滤波器

图像滤波是一种基本的图像处理方式。图像滤波的应用范围广泛，可以实现多种图像处理，可用于图像去噪[5]、分割、增强[6]、插值。图像滤波公式通常可以表示为

式中：I(x,y)表 示初始图像；U(x,y)表示滤波后的图像； Φ是 核 转 换 函 数；N(x,y)是 (x,y)的 支 持 区 域；(x,y)∈Ω 表 示空间坐标，其中 Ω是成像域。滤波器通常在局部窗口N(x,y)={(u,v)||u−x|+|v−y| ≤r}中估计平滑图像，其中r为局部窗口半径，如图1（a）所示[7]。局部滤波方法通常采用（2）式形式表示：

图1 不同类型支持区域的滤波特征Fig. 1 Diagram of filtering characteristics in different types of support regions

图1 代表了4 种不同的滤波方式。图1（a）中由于权重函数和支持区域都独立于图像内容，因此这种方式不能保留图像边缘信息[8]；图1（b）、图1(c)、图1（d）3 种滤波方式权重函数均自适应图像内容，导致计算成本明显增加[9]。本文提出的盒式滤波器的子窗口划分如图2 所示，在8 个子窗口上执行盒式滤波器，以保持边缘和边角。从图2 中的8 个支持区域中自适应选择图像支持区域，中心像素位于子窗口的边缘或边角，因此可以保留边缘和边角。滤波器没有过多计算量有两个原因，首先滤波器中的权重函数独立于图像内容，避免了对每个像素的权重函数进行评估；其次由于支持区域是可计算的（只有图2 中的8 个情况），滤波器没有要像其他方法一样为每个像素找到复杂的支持区域。

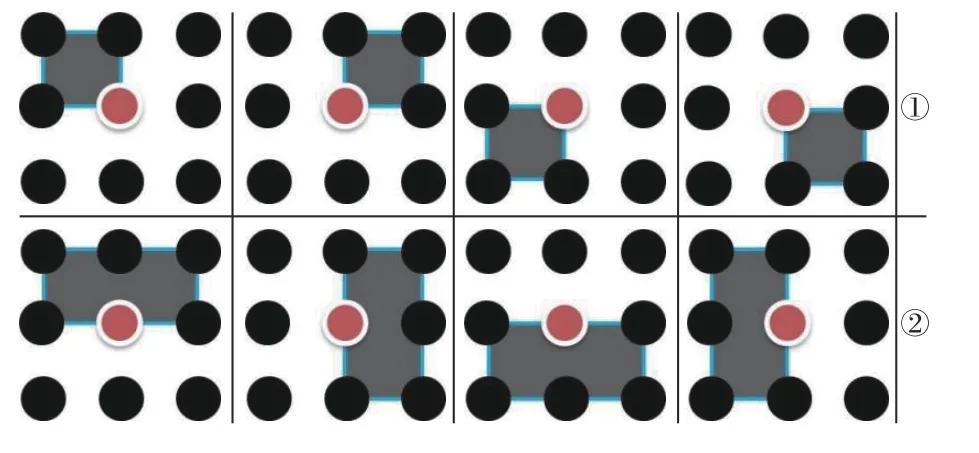
图2 中心像素位于8 个子窗口的位置Fig. 2 Center pixel located in position of eight sub windows

在支持区域中任一像素都可以被处理，因为它同时存在于4 个子窗口的拐角上(图2 中①所在行)或在两个半窗口的边缘上(图2 中②所在行)。假设中心像素U(x,y)位于一个角落或一个边缘上，子窗口回归可以以统一的方式处理角、边和平面区域。

对于给定位置 (x,y) 和窗口半径r，定义其8 个子窗口如（3）式～（10）式：

在盒式滤波器中通常改变迭代次数或窗口半径类似等价，因为两者在盒式滤波器中作用效果一致[10]，但在子窗口盒式滤波器中改变窗口半径和迭代次数会有不同的效果，如图3 所示。

图3 不同参数条件下的子窗口盒式滤波器Fig. 3 Sub-window box filter under different parameter conditions

图4 所示为子窗口盒式滤波器的执行流程。为确认对低照度图像边角和边缘保持性能，利用灰度棋盘式图像进行测试。如图5 所示，图5(a)为原始图像，图5(b)为噪声图像，图5(c)中引导滤波器的参数设置较小时滤波输出后图像较为模糊，图5(d)增大引导滤波器的参数时图像会有伪影出现，图5（e）所示的子窗口盒式滤波器在保留边角和边缘的同时消除了噪音。

图4 子窗口盒式滤波器运算流程Fig. 4 Flow chart of sub-window box filter operation

图5 引导滤波和本文滤波器保持边缘性能对比Fig. 5 Performance comparison in edge preserving between guided filter and proposed filter

原始图像经子窗口盒式滤波器得到滤波输出图像（基础层），输入图像与滤波后图像经（14）式差值运算得到包含噪声信息的图像（细节层）。

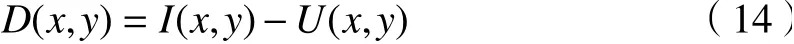
本文算法整体流程如图6 所示，通过子窗口盒式滤波器对原图像进行分层处理，在基础层图像对比度增强和细节层图像去噪后，采用光照强度自适应权重函数进行基础层和细节层的合成。

图6 本文微光图像增强算法流程Fig. 6 Flow chart of proposed low-level-light image enhancement algorithm

1.2 基础层图像处理

原始图像经子窗口盒式滤波平滑后得到的基础层图像对比度较低，容易造成背景模糊，需要对基础层图像的对比度进行增强[11]。本文从像素灰度分布出发设计一种自适应阈值直方图均衡化算法，通过（15）式、（16）式计算基础层图像直方图并进行二值化处理[12]，微光图像及直方图二值化处理前后图像如图7 所示。

图7 算法处理前后的微光图像直方图分布Fig. 7 Histogram distribution of low-level-light image before and after algorithm processing

（15）式中：H(l)为 计算得到的基础层直方图，l为该点像素值；U(x,y)为 基础层图像； δ(·)为离散时间单位脉冲函数；T为阈值，使用固定阈值会导致增强后图像出现过曝光的问题。由于像素数目越多的灰度级越重要，因此按照像素数目对直方图进行降序排序得到降序排序直方图[13]。对HBD(l)计算灰度级累积直方图得到HBDC(l)，累计直方图代表图像组成成分在灰度级的累计概率分布情况，计算公式为

式中：n1,n2,···,nk表示对应不同灰度级下小于等于此灰度值的概率；k为灰度级总数。图7 中微光图像对应的累计直方图概率分布如图8 所示。

图8 累计直方图概率分布Fig. 8 Cumulative histogram probability distribution

设置自适应阈值T为上限函数，当灰度频数P大于T时，将P值赋予T，否则P保持不变，得到的累计直方图分布函数为

式中：q表示灰度级中存在的最大灰度值；el为设定阈值前像素对应数量。设置基础层压缩后的动态范围为Pb且令Pb= 255，便于与细节层的合成操作。压缩后的基础层为

式中：fb为基础层压缩后的输出图像；ql为阈值划分后像素的对应数量。

图9 为直方图均衡化效果对比。由图9 可以看出，经直方图均衡化处理后的图像相比处理前图像在亮度上有明显提升，但图像中部分位置存在亮度过高的情况，影响视觉效果；自适应直方图均衡化算法处理后图像在对比度上有了一定提升，且没有出现大面积的过度增强现象。

图9 直方图均衡化效果对比Fig. 9 Effect comparison of histogram equalization in different scenes

1.3 细节层图像处理

细节层图像处理的重点在于去除噪声以及弱小细节的增强[14]。文献[4]算法在细节层图像处理方面采用了自适应增益控制的方法对细节层图像进行增强，该算法中采用了一种噪声模板可见度函数：

使用自适应增强算法是由于噪声模板函数与噪声可见度函数成反比关系，Mw(x,y)的大小反映了图像区域变化。自适应增益控制的原理在于根据不同区域的信息自动调整增益函数，对于细节丰富的区域进行较大程度的放大，对于相对平坦区域较小放大，这样可以在增强目标细节的同时抑制噪声的放大。自适应增强函数定义为

式中：gmin、gmax分别对应图像像素点的最低增益值和最高增益值，在噪声可见度函数趋于1 时取得gmin，在噪声可见度函数区域为0 时取得gmax。为了使图像细节信息不被抑制但又不被过度增强，最低增益通常选取为1，最高增益通常选取为2.5。图10 为微光图像细节层增强效果。

图10 微光图像细节层增强Fig. 10 Detail layer enhancement of low-level-light image

1.4 基础层与细节层的合成

文献[4]中将基础层图像和细节层图像调整到所需动态范围，将2 幅图像按照一定比例进行融合。基础层分量与细节层分量的融合表示为

式中：Rout为 融合后增强的输出图像；fb和fd分别表示基础层分量以及细节层分量；p为融合系数，范围为（0，1）。算法中固定融合系数p，若在不同照度条件下的微光环境中，固定使用系数会使图像因场景变换携带较多的模糊和噪声，图像边缘区域及弱小细节信息不能较好呈现。针对上述问题，为突出细节特征进而增强可视程度，本文引入自适应图像融合系数[15]用于微光图像合成，表达式为

式中： α为补偿增值； σ为固定指数，其作用在于控制不同微光环境下基础层融合系数与细节层融合系数的差值范围。若目标背景环境照度极低，噪声对成像产生较大干扰时，背景层系数kb范围在[0.1，0.2]时效果更佳。当背景噪声对图像的影响较小时，背景层系数kb范围在[0.2，0.4]之间效果更佳。nvalid为基础层直方图分布中的有效灰度值个数总和，继而通过有效灰度值个数占整个灰度级的比例来对图像的基础层融合系数kb进行确定，比例不同代表了不同照度环境下的信息不同，在得到基础层融合系数后，细节层分量的融合系数可表示为

式中：kd为细节层分量融合系数。

基础层图像和细节层图像的融合系数分别得到确定后，融合后的输出图像可以表示为

2 实验仿真与分析

2.1 实验平台介绍

微光实验平台实物图如图11 所示。其中：MPPC有优异的光子探测效率、高增益、良好的时间分辨率和宽光谱响应范围，在极微弱光环境下拥有较好的光子计数能力，能够实现在1 0−4lx以及更低照度条件下的实物物体探测扫描；光学成像结构包括镜头遮光罩、支架；扫描机构是由二维导轨和一个光纤耦合器组成，光纤耦合器用来固定MPPC探头，二维导轨在水平方向和垂直方向带动探头移动；钨灯光源用来模拟预设不同的微光环境，给实验环境提供不同的光照大小和光照位置；KWZ-2000 宽量程照度计用来测量整个实验平台内部环境的光照大小，其测量的光照度范围为1 0−7lx ∼10−3lx。

图11 实验平台实物图Fig. 11 Physical drawing of experimental platform

微光实验平台内部结构如图12 所示，实验平台以MPPC 探测器为核心，结合光学成像结构，实现微光环境下目标物体成像。入射的微弱光照射在目标物体的表面，物体表面的光子经反射后在镜头后方形成一个像面，由扫描机构带动MPPC探测器的探头移动进行逐点扫描，光纤将扫描后的计数值传输到计算机存储器，对数据处理后生成二维图像。

图12 实验平台内部结构Fig. 12 Internal structure of experimental platform

2.2 实验结果与分析

用钨灯光源在微光实验平台上分别模拟3 种不同照度的微光环境，微光实验平台获取的A、B、C 3 组原始图像如图13 所示。

图13 不同照度下获取的原始图像Fig. 13 Raw images obtained at different levels of illumination

微弱光条件下光子计数探测系统存在增益值过低或过高的情况，得到的输出图像对比度较低；另一方面由于MPPC 探测器自身的光电元件和探测环境引入了大量随机噪声，使得图像的边缘和细节信息较为模糊。为验证本文算法处理光子计数微光图像的有效性，分别用文献[9]交叉子窗口算法、文献[3]DDE 算法、文献[4] DDE 改进算法以及本文算法对原图像进行校正处理，得到的实验结果如图14～图16 所示。

图16 1 0−5 lx微光环境下各算法增强图像效果对比Fig. 16 Comparison of effect of image enhancement by algorithms under 1 0−5 lx low-level-light condition

在图14～图15 中可以看出，（a）列交叉子窗口算法对原始图像进行了噪声滤除，但图像整体亮度改善不明显；（b）列DDE 算法处理的图像亮度虽然得到提升，但整幅图像对比度和轮廓细节并没有获得明显改善；（c）列中文献[4]算法和（d）列本文所提算法较之前算法在图像细节上都取得了更好的增强效果，强化了细节信息，但本文算法在增强边缘特性上更加突出，在增强细节信息的同时抑制了边缘光晕伪影现象产生。

图14 1 0−1 lx微光环境下各算法增强图像效果对比Fig. 14 Comparison of effect of image enhancement by algorithms under 1 0−1 lx low-level-light condition

图15 1 0−3 lx微光环境下各算法增强图像效果对比Fig. 15 Comparison of effect of image enhancement by algorithms under 1 0−3 lx low-level-light condition

通过图16 可以看出，（a）列中交叉子窗口算法较好地保持了模型的轮廓结构信息，但由于噪声的存在图像细节信息没有得到较好的增强；（b）列中采用DDE 算法处理后的图像细节特征得到了进一步的增强和凸显，但该方法基础层和细节层的融合比例设置为固定值，导致细节层所占的比重过大，造成了图像边缘比较模糊，没有给人较好的视觉效果；（c）列中文献[4]算法在图像对比度上有了明显改善，由于实验环境的光照极度微弱，图像边缘信息增强不够明显；（d）列所示的本文算法在提升对比度和丰富细节的同时增强了图像边缘轮廓信息，汽车的前轮、夹子的转轴 、书架的底座等边缘细节信息较之前算法都有了较好的视觉呈现。

综合图14～图16 可以看出，在3 组实验中经本文算法处理的图像都有了较好的增强效果；DDE算法和文献[4]算法在前两组实验中对图像增强也有较好的效果，但随着实验环境中光照强度的降低，在第3 组实验中前3 种对比算法处理后的图像轮廓信息不够丰富，细节信息得不到凸显，而本文算法依然可以在增强细节的同时突出边缘信息。本文算法在3 组照度环境下对图像的增强效果都较为清晰，验证本文算法场景自适应能力较强，能够自适应不同微光环境而对图像进行增强。

为了客观比较不同算法对光子计数微光图像增强的有效性，从标准差、信息熵、平均梯度、运算时间4 个方面对每种算法的处理结果进行客观对比和分析。

由表1 中数据可以看出，A 组信息熵相对稳定，即在该微光条件下图像所携带信息量相对稳定， C 组中经本文算法处理后的信息熵较之前算法在数值上均有提高，表明本文算法获取的图像细节信息更为丰富，边缘轮廓得到更好的呈现；由表1～表2 中数据可知，本文算法标准差数值高于其他算法，这说明本文算法在微光环境中有效提升了图像的对比度；表3 中经本文算法处理后的图像信息熵数值小于改进前算法,表明经本文算法处理的极微弱光图像信息较之前算法稳定，受光强条件限制图像所携信息量不充分，凸显的细节较为集中；由表1～表3 组实验数据的平均梯度可知，本文算法较之前算法在梯度值上有了显著提升，表明经本文算法处理后的图像清晰度得到较大提高。

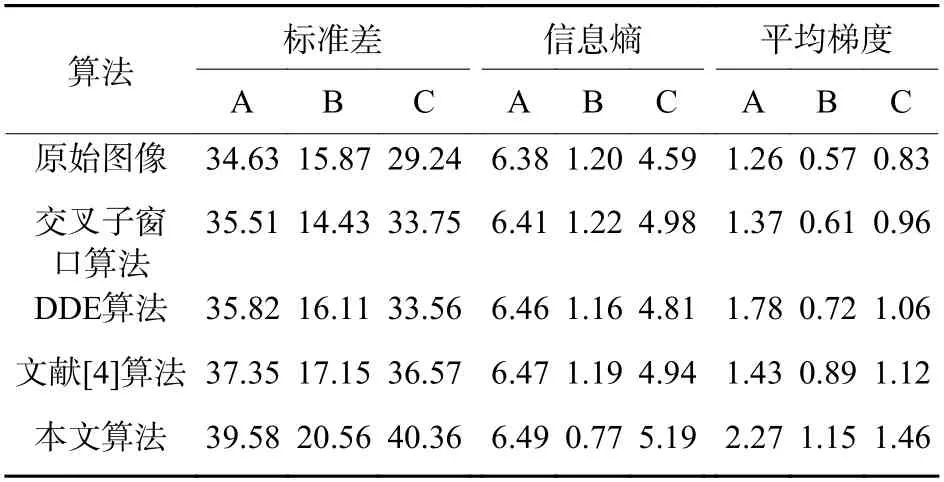
表1 1 0−1 lx微光环境下的图像增强评价指标Table 1 Image enhancement evaluation indexes under 10−1 lxlow-level-light environment

表2 1 0−3 lx微光环境下的图像增强评价指标Table 2 Image enhancement evaluation indexes under 10−3 lxlow-level-light environment

表3 1 0−5 lx微光环境下的图像增强评价指标Table 3 Image enhancement evaluation indexes under 10−5 lxlow-level-light environment

选取图14～图16 中的小车图像作为评价图像，对不同微光环境下各算法的运行时间进行比较。由文献[4]可知，文献[4]算法计算时间优于DDE 算法，故仅将本文算法与交叉子窗口算法和文献[4]算法进行运算时间比较，对比结果如表4所示。

表4 4 种算法运行时间对比Table 4 Comparison of running time of four algorithms s

本文采用的子窗口盒式滤波器在空间支持区域上只有特定的8 种情况，减少了对复杂空间支持区域的搜索时间；另外本文对基础层图像的灰度值进行动态范围压缩，减少了运算时间。根据表4中算法运行时间的结果可知，本文算法处理3 组微光环境下的图像耗时较短，且优于其他算法。

3 结论

本文为解决多像素光子计数器探测微光图像容易出现的边缘信息模糊问题，提出了一种基于子窗口盒式滤波的自适应图像增强算法。利用图像的中心像素位于8 个子窗口的边缘或角落的特性来执行盒式滤波器，从而更好地保持图像的边缘、边角信息。利用滤波后的基础层图像中的有效灰度值个数对目标环境照度级别进行判断，根据有效灰度值个数所占总灰度比重自适应地确定融合系数，实现不同级别微光条件下图像噪声的抑制和边缘轮廓信息的增强。与改进前算法进行比较可知，本文算法随着光照强度的减弱对图像依然有较好的增强效果，在抑制噪声和增强边缘轮廓信息上也有一定的优越性，在微光图像处理等领域有良好的应用前景。