SSJNMF算法识别基因-药物共模块探讨

马敬山，毛玉杰，张 杉，3

(1.石家庄邮电职业技术学院，石家庄 050022； 2.燕山大学 理学院，河北 秦皇岛 066004；3.中车唐山机车车辆有限公司，河北 唐山 063000)

许多研究者陆续完成了CCLE[1]、GDSC[2]等多项癌症基因组计划。研究表明，在高维基因表达数据和抗癌药物反应数据中，识别具有统计学和生物学意义的基因-药物共模块，有助于理解抗癌药物的分子机制，筛选潜在的药物靶点。Kutalik等使用NCI-60数据[3]完成了初步实验，获得了Ping-Pong算法[4]。Chen等提出了多矩阵分解算法(NetNMF)[5]，基于基因组数据构建的相似网络矩阵，使用三元非负矩阵分解，来寻找公共模块和模块之间的关联。Wang等在非负矩阵分解模型的基础上，通过向分解因子添加L1-范数规范约束，提出了RNMF算法[6]。Zhang等提出了具有网络正则性约束的改进的联合非负矩阵分解算法(JNMF)[7-8]。

受上述算法的启发，提出了一种带相似约束的稀疏联合非负矩阵分解算法(SSJNMF)，并将其应用于基因药物共模块识别的GDSC数据集。

1 数据和算法

1.1 数据源和预处理

下载同一细胞系对应的最新基因表达数据和药物反应数据，发现药物反应数据缺失值，数据预处理如下：

删除缺失值大于30%的列，其余203列对应203种药物，用mice包进行基因填充[9]，以获得完整的药物反应矩阵。

记基因表达矩阵为G1∈R915×17 737,记药物响应矩阵为G2∈R915×203，利用皮尔逊相关系数作为工具，获得基因相似性矩阵X11、药物相似性矩阵X22、基因与药物相似性矩阵X12。取矩阵X11、X22和X12的绝对值，同时将输入数据完成[0,1]均值处理[10]，以保证输入数据(G1,G2)和相似性数据处于相同的数量级。

1.2 算法构造

基于文献[7]中识别多维模块的思想，将基因相似性数据、药物相似性数据和基因药物相似性数据添加到联合非负矩阵分解算法中，完成“带相似约束的稀疏联合非负矩阵分解算法”的构造，简称SSJNMF，根据降维后的数据确定模块数，计算后限制分解因子，最后筛选模块数据，目标函数如下：

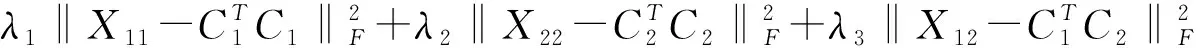
1.3 算法求解过程

Lee和Seung提出的乘法器更新迭代算法[11]优化SSJNMF模型，以保证变量B和C的凸性，并获得全局最优解：

扩展SSJNMF模型如下：

(1)

(2)

(3)

(4)

(5)

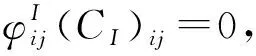
(6)

(7)

(8)

SSJNMF算法的求解过程：

第一步：用B、C1和C2为初始值，代入模型第一部分，得到SSJNMF的初始迭代矩阵。

第二步：按照(6)、(7)和(8)交替更新矩阵B,C1和C2。

第三步：重复第二步，终止条件为误差小于10-6或次数到达500次。

2 结果分析与比较

2.1 SSJNMF算法的识别过程及识别结果

识别的第一步是分析统计显著性，通过比较常用模块中基因与药物信息的相关性，分析算法识别结果的统计显著性，具体步骤如下：

一是以共模块为单位，从G1和G2中筛选出子矩阵sG1和sG2，按列求皮尔逊相关系数：

系数之和表示为：

二是将基因表达数据和药物应答数据按列重新排列，选岀1 000个维度相同的随机共模块，Srand用于表示每个随机共模块各列相关系数之和。

三是在1 000个Srand所形成的分布下，估计岀Sreal所对应的概率分布统计值P1 (大于Sreal的比例)。若P1<0.05，可以认为它不服从1 000个分布的置信区间之外的随机分布，即结果是可行的和可解释的，相反共模块服从随机分布。此外，非参数秩和检验的实验结果也被用来推断服从的分布，将其置于分布之下并计算出相应的概率分布统计值P2，如果P2<0.05/k，实验结果具有统计学意义。

辨识的第二步是确定参数，并通过控制变量法调整参数来选择最优参数。表1为不同参数组合下的统计结果，其中，Num1为非空且不服从随机分布的共模块个数，Num2为药物模块为空的共模块个数，Num3为非空且通过非秩和检验的共模块个数。结果表明，当λ1=0.1、λ2=150、λ3=0.5时，识别出的具有统计意义的共模块最多。

表1 不同参数组合下的统计结果Tab.1 Statistical results under the combination of different parameters

表2为当λ1=0.1、λ2=150、λ3=0.5时，调整γ1、γ2、k的部分统计结果，其中Num4为富集分析后有生物意义的基因模块个数，通过综合分析P1[P1=Num1/(70-Num2)]，P2[P2 =Num3/(70-Num2)]以及具有生物意义的共模块所占的比例P3[P3=Num4/(70-Num2)]及综合表1，可以得岀以下结论：当参数λ1=0.1、λ2=150、λ3=0.5、γ1=0.5、γ2=0.5、k=70时，SSJNMF算法识别岀的70个基因-药物共模块为最优结果(模块个数由阈值T决定，当T=3.7时，识别的70个共模块指标最优[12])。

表2 固定λ1、λ2、λ3调整γ1、γ2、k的统计结果Tab.2 Statistical results of adjustment of γ1、γ2、k under fixed λ1、λ2、λ3

2.2 共模块的生物功能分析

借鉴Mao等人[13]提岀的生物功能分析方法，分析SSJNMF算法识别岀的68个有意义的共模块，结果表明，有60个模块的药物个数大于1。表3列举了第18和第46个共模块的生物功能分析结果。表中，ID:共模块序号；G:对应模块中的基因；D:药物个数。

表3 部分基因药物共模块的生物功能分析结果Tab.3 Results of biological function analysis of some gene-drug common models

生物功能相关分析结果表明，每个基因模块的GO生物功能项所富集的生化过程与相应药物模块中药物靶向的信息之间存在着很强的相关性。

2.3 三类算法的识别结果比较

为了更好地说明SSJNMF的识别性能，在同一数据集上执行了NetNMF[6]和 JNMF[8]，识别岀各自的70个基因-药物共模块。结果如表4。可以看岀，SSJNMF得到的P1和P2均比NetNMF和JNMF高，说明SSJNMF识别的共模块有更强的统计意义。

表4 三种算法识别的共模块的统计意义对比分析Tab.4 Comparative analysis of statistical significance of common modules of three algorithm identification

3 结论

SSJNMF算法是有效的基因-药物共模块的识别工具，识别结果具有很强的统计意义和生物意义。基因模块的GO生物功能项所富集的生化过程与对应的药物模块中药物所靶向的信息之间具有强关联性。SSJNMF筛选岀的部分结果可能存在信息相似情况，后期可以进行合并处理，以进一步提高共模块识别的有效性。